基于IMM的機動目標卡爾曼跟蹤濾波算法

李越強

(解放軍91977部隊，北京 100036)

0 引 言

機動目標跟蹤問題一直是人們研究的重點，為了實現機動目標高精度穩定跟蹤，首先要建立與實際目標運動相匹配的目標運動模型[1-2]。而常規跟蹤濾波算法對目標跟蹤時基于某一種運動模型，因此難以適應機動目標隨時改變運動狀態，針對機動目標跟蹤，目前常用的有多模型、交互式多模型(IMM)、切換模型等方法[3-4]。多模型方法就是對一組不同機動模型分別進行跟蹤濾波，最終的參數估計是各濾波器估計值的加權和。在多模型基礎上，Bar-Shalom提出了交互式多模型方法，這一方法對無序目標的機動檢測顯示了更好的魯棒性和跟蹤的穩定性。切換模型則是分別建立機動和非機動運動模型，利用機動檢測實現在這2個模型之間的切換[5-7]。一般來說，IMM的跟蹤性能較好。

本文對二維空中機動目標進行了研究，首先對機動目標跟蹤原理、Kalman濾波算法以及IMM方法原理進行了闡述，并采用Kalman濾波算法對基于單模型和IMM機動目標跟蹤進行了仿真比較分析。

1 機動目標跟蹤原理

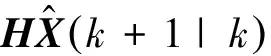
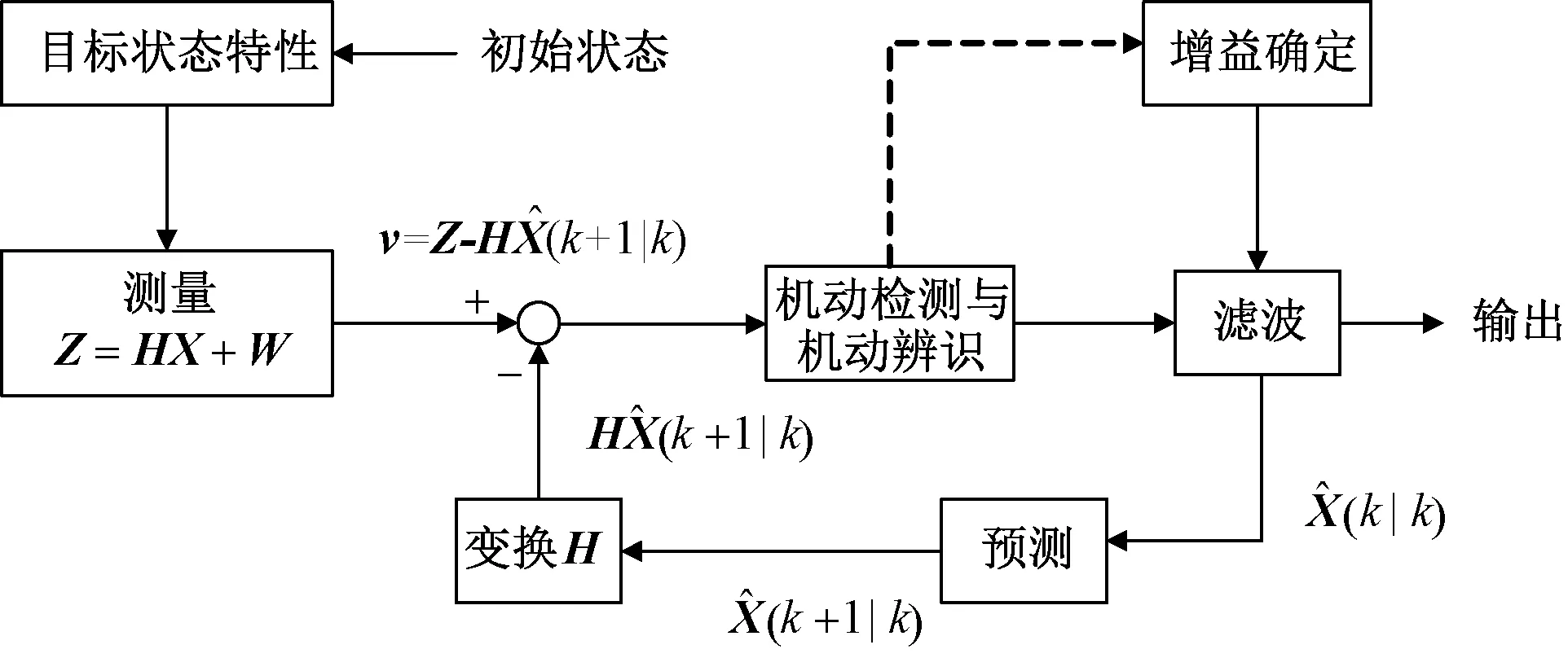
圖1 機動目標跟蹤基本原理圖

2 機動目標跟蹤算法

2.1 卡爾曼濾波算法

卡爾曼濾波器目標基本運動模型：

X(k+1)=Φ(k+1,k)X(k)+Γ(k)W(k)

(1)

式中：X(k)為當前k時刻目標運動狀態向量；Φ(k+1,k)為目標狀態從k時刻到k+1時刻的狀態轉移矩陣；Γ(k)為系統模型噪聲系數矩陣。

基于式(1)模型目標觀測方程，有：

Z(k+1)=C(k+1)X(k+1)+V(k)

(2)

式中：W(k)為模型量測噪聲協方差矩陣；W(k)、V(k)為均值、高斯隨機序列。

卡爾曼濾波算法基本步驟如下：

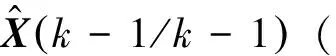
(3)

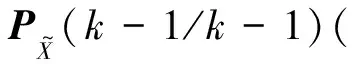
ΦT(k,k-1)+Γ(k-1)Q(k-1)ΓT(k-1)

(4)

(3) 當前k時刻卡爾曼增益計算：

(5)

(4) 計算當前k時刻濾波估計:

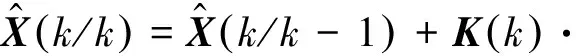
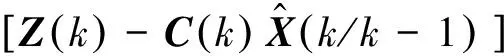
(6)

(5) 計算當前k時刻濾波誤差方差陣:

(7)

卡爾曼濾波算法計算濾波估計及濾波增益和協方差矩陣計算流程圖如圖2、圖3所示。

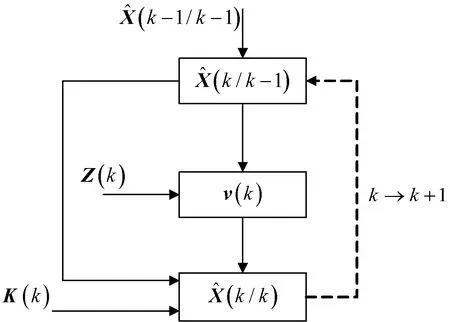
圖2 計算濾波估計流程圖

圖3 卡爾曼濾波增益和誤差方差陣計算流程圖

在應用卡爾曼濾波算法時，需要指定濾波器起始條件，可根據目標的初始狀態計算出卡爾曼濾波器起始條件。起始條件的建立參考文獻[3]中有詳細描述，在此不再贅述。

2.2 交互多模型方法

IMM方法中，每一個運動模型對應著相應的濾波器，具備多個濾波器、1個模型概率估計器、1個交互式作用器和1個估計混合器，通過多個模型相互作用跟蹤1個機動目標，具有r個模型的IMM方法原理框圖如圖4所示。

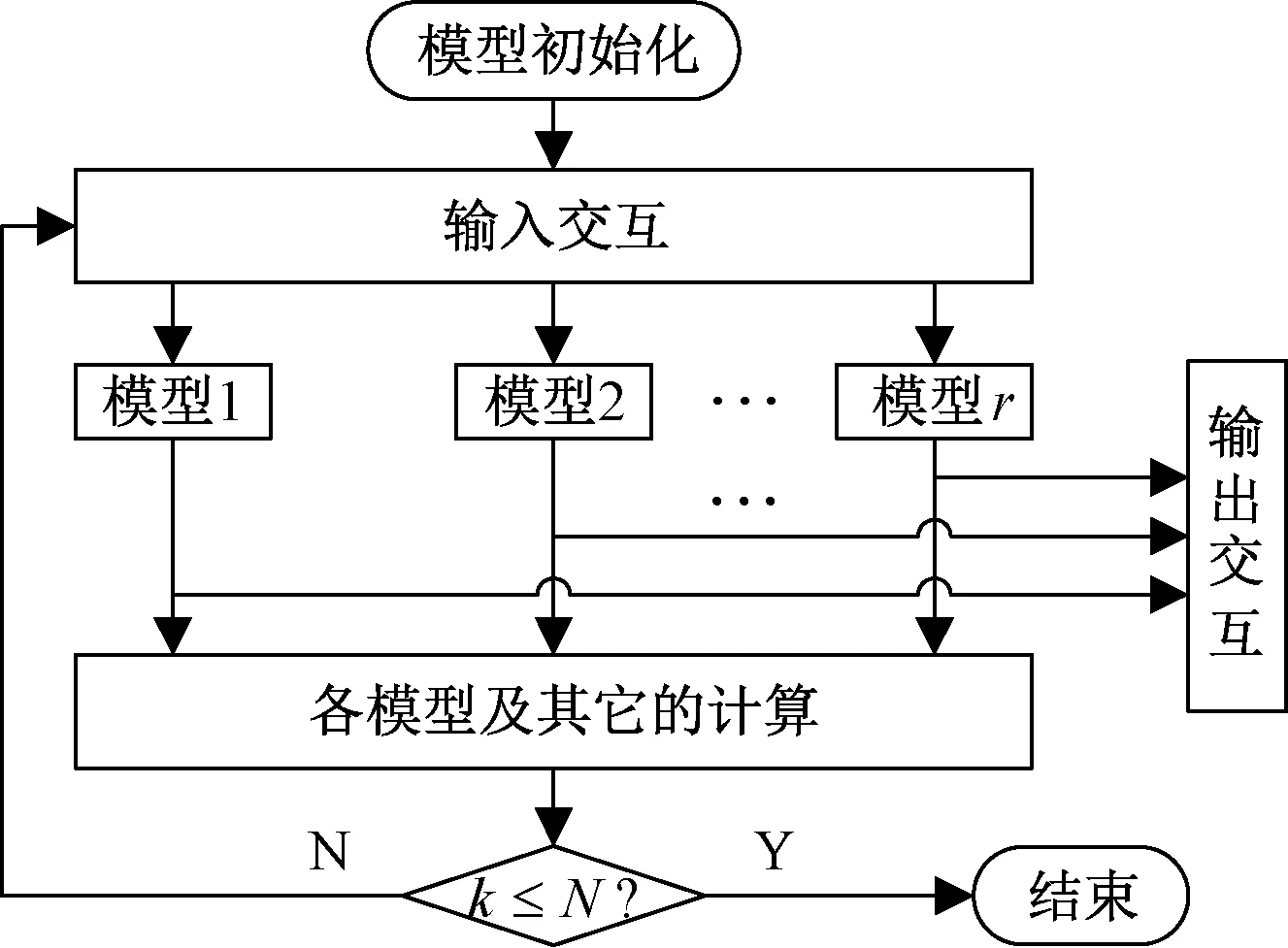
圖4 IMM方法原理框圖

假設IMM方法中各模型間切換概率是基于馬爾科夫鏈計算的，那么各個模型交互作用器利用模型概率和模型轉移概率類計算每一個濾波器的交互作用。從模型i轉移的模型j的轉移概率為pij，馬爾科夫鏈轉移概率矩陣如下：

(8)

IMM方法濾波循環開始后，每一個濾波器利用多個模型交互式估計和測量數據計算出一個新的估計和模型的可能概率，然后，前一時刻的模型概率、模型可能性、模型轉移概率被用來計算新的模型概率，那么總的狀態就可以通過新的狀態估計以及相應的模型概率計算出來。

基于馬爾科夫鏈的交互多目標概率切換計算的IMM方法步驟如下：

(1) 輸入交互：

(9)

其中：

(10)

Poj(k-1/k-1)=

(11)

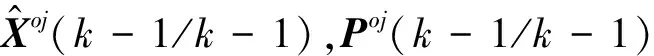
(3) 模型概率更新計算

若第k時刻，模型Mj(k)的濾波殘差為υj(k)，相應的協方差為Sj(k)，假設服從高斯分布，則模型Mj(k)的可能性為：

Λj(k)=P{Z(k)/Mj(k),Zk-1}=

(12)

其中：

(13)

模型Mj(k)的概率更新為：

(14)

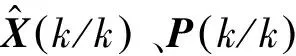
(15)

(16)

3 仿真分析

采用卡爾曼濾波算法對基于單模型和IMM機動目標跟蹤濾波仿真，IMM包含3種模型：模型1為勻速直線運動模型，模型2為右轉機動模型，模型3為左轉機動模型。分別利用IMM和以上3種單個模型對機動目標進行跟蹤。3種模型狀態轉移矩陣分別為：

(17)

(18)

(19)

式中：T目標采用時間間隔，取值1 s；ω為目標轉彎角速率，取值3°/s。

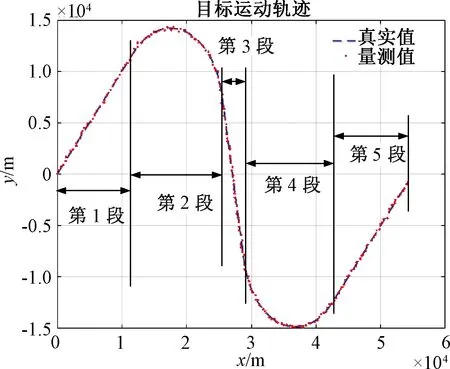
圖5 目標運動軌跡

分別采用IMM方法以及3種單模型(勻速直線、左轉、右轉)的Kalman濾波對該機動目標進行跟蹤，其濾波后軌跡、IMM方法模型概率曲線、不同模型濾波的x/y坐標位置誤差以及不同模型濾波的x/y方向速度誤差分別如圖6～圖11所示。

圖6 基于IMM、模型1、模型2以及模型3四種Kalman濾波軌跡結果

通過圖6、圖8、圖9、圖10和圖11可以看出，采用模型1對機動目標進行跟蹤濾波時，與模型1相匹配的第1、3、5段軌跡的位置和速度跟蹤誤差相對于其他模型更小，濾波后軌跡在第1、3、5段更接近真實軌跡；由于其他軌跡段與模型1不匹配，在其他軌跡段出現了較大的位置和速度跟蹤誤差，其他軌跡段濾波后軌跡較真實軌跡有較大偏差。

圖7 基于IMM方法濾波模型概率曲線

圖8 IMM與單模型濾波x位置跟蹤誤差比較

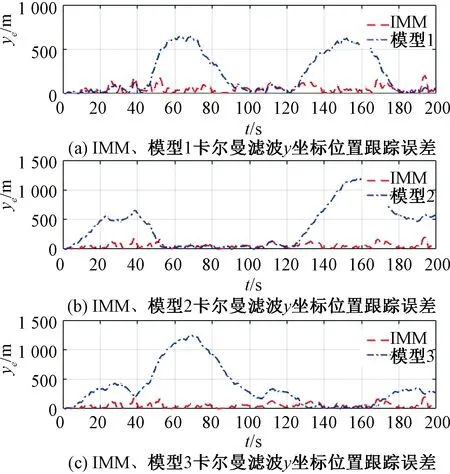
圖9 IMM與單模型濾波y位置跟蹤誤差比較

圖10 IMM與單模型濾波x速度跟蹤誤差比較

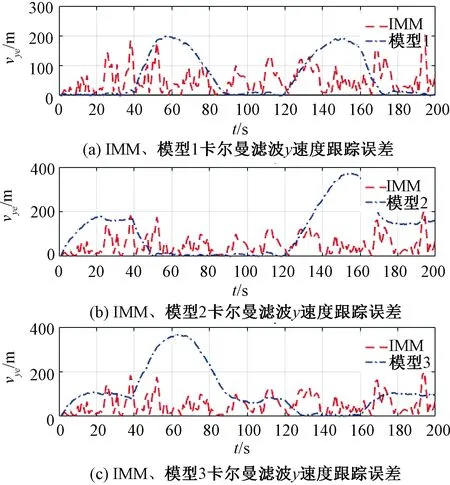
圖11 IMM與單模型濾波y速度跟蹤誤差比較

采用模型2對機動目標進行跟蹤濾波時，與模型2相匹配的第2段軌跡的位置和速度跟蹤誤差相對于其他模型更小，濾波后軌跡在第2段更接近真實軌跡；由于其他軌跡段與模型2不匹配，在其他軌跡段出現了較大的位置和速度跟蹤誤差，其他軌跡段濾波后軌跡較真實軌跡有較大偏差。

采用模型3對機動目標進行跟蹤濾波時，與模型3相匹配的第4段軌跡的位置和速度跟蹤誤差相對于其他模型更小，濾波后軌跡在第4段更接近真實軌跡；由于其他軌跡段與模型3不匹配，在其他軌跡段出現了較大的位置和速度跟蹤誤差，其他軌跡段濾波后軌跡較真實軌跡有較大偏差。

采用IMM方法對機動目標進行跟蹤濾波時，由圖7可知，在各段軌跡中，第1、3、5段軌跡與模型1更匹配，在該3段軌跡中模型1的概率比其他模型更高；第2段軌跡與模型2更匹配，在該段軌跡中模型2的概率比其他模型更高；第4段軌跡與模型3更匹配，在該段軌跡中模型3的概率比其他模型更高。IMM濾波預測輸出結果由各模型濾波結果加權輸出，但主要由匹配度較高的模型濾波結果確定。

圖12為采用該算法對無人機跟飛實測數據，圖13和圖14分別為無人機X和Y方向的運動狀態和跟蹤誤差。從實際數據可以看出該算法在無人機機動時，能很好地跟蹤目標，且在進入穩定航跡后，跟蹤誤差逐漸收斂，具有良好的跟蹤效果。

圖12 無人機運動軌跡

圖13 無人機各方向運動狀態

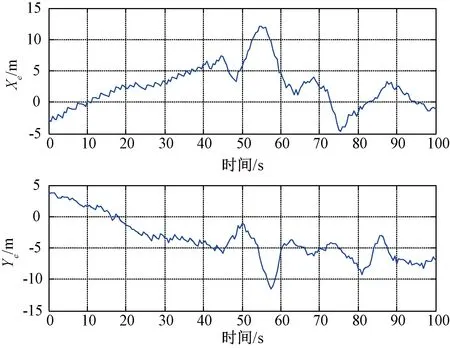
圖14 無人機各方向濾波跟蹤誤差

在目標進行機動時，基于IMM跟蹤濾波可實時更新計算各模型概率。與當前軌跡匹配最高的模型概率更大，IMM跟蹤濾波結果受匹配度更高模型的濾波影響也就更大，使得目標機動全程均能很好地對其跟蹤濾波，相較于采用單模型對機動目標跟蹤濾波，具有更高的濾波精度。但由于IMM方法包含多種模型，跟蹤濾波時，多種模型同時跟蹤濾波，且還需更新計算模型概率以及交互計算等，相較于單模型跟蹤濾波，計算量更大，對硬件要求更高。

4 結束語

本文主要對基于IMM機動目標卡爾曼跟蹤濾波算法進行闡述，IMM機動目標跟蹤能夠實時選擇與當前目標運動匹配度最高的模型濾波主導IMM輸出結果，相較于單模型僅能對機動目標中與該模型相匹配的一段運動軌跡進行高精度跟蹤，IMM能夠實現機動目標全程較高精度穩定跟蹤。理論上只要IMM包含的模型種類足夠多，且機動目標各階段總能與IMM中某一種模型相匹配，IMM就能實現對機動目標高精度全程穩定的跟蹤，但考慮到IMM的計算量以及實際機動目標運動模型，IMM一般包含幾種典型運動模型以及適合的模型參數庫就能很好地對機動目標進行跟蹤。