基于離散元的木質板鋪料機結構優化分析

賴大港，賀福強，徐浩然，薛亞軍

（550025 貴州省 貴陽市 貴州大學 機械工程學院）

0 引言

重組木是人造板材一種，是把速生小徑材、枝椏材及制材邊角料等廉價低質材料經碾搓設備加工成橫向不完全斷裂，縱向松散而又交錯相連的網狀木束，再經干燥、施膠、鋪裝和模壓（熱壓）而制成的一種新型的木材[1]。攤鋪機起源于國外，最早主要應用于鋪設瀝青路面，后來廣泛應用于各類工業生產廠房中作為生產線的一部分，近幾十年來，國內開始出現攤鋪機，雖然起步較晚，但發展迅速，現今鋪料裝置技術應用成熟，廣泛用于煙草、陶瓷工藝、食品加工、建筑材料加工等各種生產中。在對鋪料裝置進行的不同研究中，南文光[2]等利用并對比了刮刀鋪粉與輥子鋪粉的粉堆內部顆粒的動力學特性差異與鋪粉層的質量；王偉[3]等對新型陶瓷零件快速成型機鋪料機做了結構優化；周志勇[4]對粉體物料在混合機內的運動和混合均勻度分布情況進行了分析；毛婭[5]等對不同攪拌速度下的粉煤灰和污泥顆粒進行了混合均勻度的分析；徐永杰[6]等分析表明，采用平行四邊形攤鋪推進法可有效提高瀝青混合料面層的均勻度；于槐三[7]利用振搗功率分析，得到保持攤鋪速度恒定就能保證壓實度在路面縱向上是均勻分布的；高向瑜[8]對車載解捆鋪料裝置的關鍵部件進行離散元仿真分析表明：三角形撥料刀齒刮撥阻力小，切繩效果好，刮撥量大，比圓柱形齒效果更好；阮國平[9]等利用數學模型對瀝青攤鋪進行參數分析，探討了振搗梁前緣角及其水平底面寬度對壓實均勻度和平整度的影響；鄭軍輝[10]分析了粒徑分布對鋪粉層密度的影響，認為鋪粉層均勻性隨粒徑分布標準差增大而變差；Parteli[11]等及Haeri[12]等分析了輥子鋪粉的輥子平移速度的增加會導致鋪粉層質量降低。以上相關研究是對不同鋪料類型的鋪料質量及均勻度的影響的分析。

本文所研究的鋪料過程是加工多功能木質板材的重要工序之一。前道工序為攪拌，物料從攪拌倉中掉落到出料倉，經出料倉傳入水平鋪料輸送帶上；后道工序為模壓成型，其緊密程度與合格率除了和本道工序的相關參數有關，很大程度取決于前期的攪拌過程與鋪料過程。此文從某廠多功能木質板材的生產制造出發，通過了解現有的生產線生產流程，選擇合適的攤鋪方式，以此確定整體的結構設計和控制方案的設計，通過模擬木料散狀鋪料運輸加工處理過程的行為特征，以對鋪料機構進行結構優化。通過離散元素法仿真，分析鋪料過程不同結構參數下物料的動態運行效果。離散元素法（Discrete Element Method）的基本原理是，將研究對象劃分為一個個相互獨立的單元，根據單元之間的相互作用和牛頓運動定律，采用松弛法進行循環迭代計算，確定在每一個時間步長所有單元的受力及位移，并更新所有單元的位置[13]。DEM 是一種分析仿真粒子間接觸行為的數值方法，應用于工業中的設計及優化，相比有限元法，能很好地解決大變形、破壞、斷裂及多物體間的碰撞接觸問題。

1 鋪料裝置的基本結構與工作原理

如圖1 所示為鋪料機結構裝置模型。整個工作流程實現了自動化，其特征在于：調整裝置、鋪料裝置、運輸裝置，由位于上部分的鋪料裝置與下部分的輸送帶共同完成一個工作流程。上部分的鋪料裝置由電機驅動的鏈輪與鏈條帶動4 個不同的葉片式滾筒和一個壓實筒同時工作，調節長螺栓用以改變不同葉片式滾筒與壓實滾筒的高度來加工不同厚度的多功能木質板材；下部分的輸送帶主要運輸板材模具，為后續的木質板材模壓成型提供保障。其中，裝置中的電機均采用PLC 控制驅動，使新型多功能木質板材的下端鋪料裝置的工作過程更加流暢，從而得到較好的工作效果。

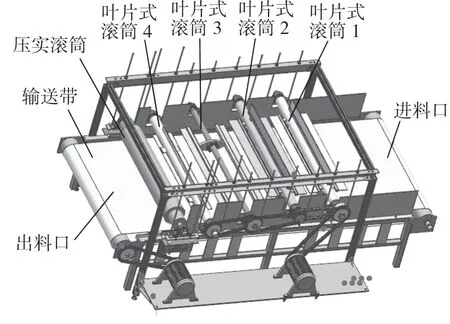
圖1 鋪料機三維模型Fig.1 Three-dimensional model of spreader

根據實際情況與要求，具體工作過程如下：

（1）電機帶動鏈輪與鏈條驅動傳送帶主滾筒進行工作，致使輸送帶帶動板材模具進入相應區域進行鋪料。

（2）4 個不同的葉片式滾筒在不同的轉速下進行轉動，以此來使物料攤平均勻。葉片式滾筒1 使鋪料機構在鋪料運轉中實現均勻鋪料，主要將最開始掉落下來的木料進行第一次攤鋪，固定葉片較長，推開幅度較大；葉片式滾筒2 的結構與葉片式滾筒1 一樣，只是固定葉片較短一些，攤鋪物料時，推開幅度較小。物料在經過前面滾筒的作用后，大部分已經攤鋪均勻，但還需要再進一步的攤鋪開均勻化，根據設計要求，此時的轉動軸所需的轉速較大且葉片較長，因此葉片式滾筒3 軸上設計為兩扇可替換的旋轉葉片來進行工作。物料在經過前面滾筒的作用后，幾乎已攤鋪均勻，對于偶然出現的局部地方高低不平處還需調整，根據設計要求此時葉片式滾筒4 降低高度，旋轉的葉片變短，近距離接觸到平鋪面，推填均勻。

（3）經過前面4 個滾筒葉片的運作，此時的木料基本平鋪均勻但疏松易發生脫落，故在輸送帶傳送板材模具時，需要壓實滾筒初步壓實木料以初步定形，防止其松散脫落。采用調節彈簧固定在壓實滾筒的下部支撐，下壓強度在一個范圍之類，更加具有靈活性、可調性。

2 顆粒模型與力學參量

2.1 顆粒模型的運動方程

由于顆粒之間的碰撞會有粘彈性，故采用軟球模型把顆粒間接觸過程簡化為彈簧振子的阻尼振動，如圖2 所示，其運動方程為

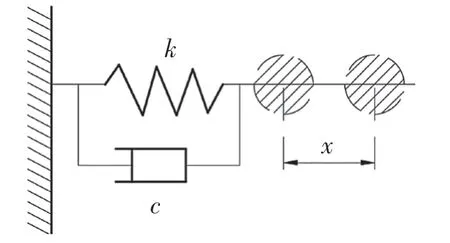
圖2 軟球振動模型Fig.2 Soft ball vibration model

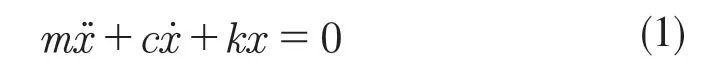
式中：x——偏離平衡位置的位移；m——振子質量；c，k——彈簧阻尼系數和彈性系數。從式（1）可看出，顆粒所受恢復力和位移大小成比，所受粘滯阻力與速度大小成正比，方向相反，因此彈簧振子的能量逐漸衰減[14]。此時材料阻尼為內部顆粒摩擦、缺陷變化，機械能轉化為熱能，能量在內部就被部分消耗掉。

學生要提高自我約束的能力。[4]高職院校管理相對高中較為松散，而學生的自我控制能力較差，容易導致整體學習積極性不高，學習風氣差。因此，學校要加強管理，學生要強化自我約束意識，加強紀律觀念，時刻銘記校風校紀，并以校風校紀約束自己。

2.2 力學參量

木質顆粒表面是粗糙、凹凸不平的，顆粒之間有咬合作用。木料的內力有內黏聚力、內摩擦力及表面張力。內黏聚力使木料之間相互黏結，增加木料抗剪切強度；內摩擦力使木料顆粒間發生位移時阻力增加；表面張力使木塊保持一定外形，木料內力大小顆粒尺寸、木料塑性及含水量有關[1]。離散元仿真時模擬真實顆粒。根據木質原材料混合特性，在仿真軟件中設置為4 種大小球形顆粒、設置接觸模型為線性粘彈性接觸顆粒模型（Linear Cohesion），結合無滑動接觸模型Hertz-Mindlin 共同作用。該模型是以Mindlin 的研究成果[15]作為理論基礎。

木料之間的碰撞不是完全彈性的，伴隨著能量損失，故離散元系統需要引入阻尼進行能量耗散。在前4 個滾筒葉片作用時，顆粒在接觸后又脫離，接觸模型為欠阻尼系統；在壓實滾筒作用時，顆粒接觸后粘結，此時為過阻尼系統。

接觸剛度的力與位移呈線性關系，即

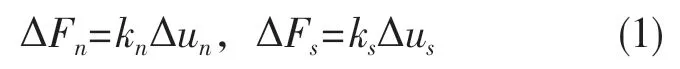
式中：kn——法向剛度；ks——切向剛度，顆粒之間存在法向力與切向力、法向位移與切向位移。

如圖3 所示，顆粒i 在慣性或外力作用下在點C 與顆粒j 接觸，虛線表示開始接觸時顆粒i的位置。隨著兩顆粒相對運動，顆粒表面逐漸變形并產生接觸力。在木質物料軟球模型中不考慮變形細節，僅計算法向重疊量α和切向位移δ，進而得到接觸力。

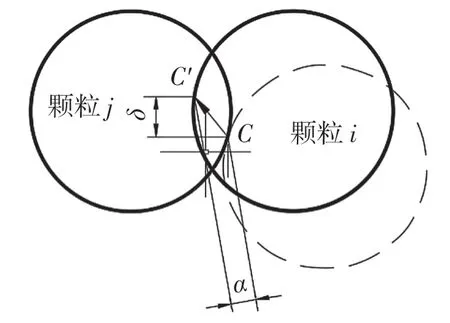
圖3 顆粒接觸模型Fig.3 Particle contact model

法向力為

滾動摩擦的影響非常重要，在接觸面上施加一個力矩來表示為

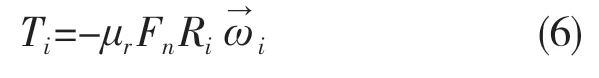
3 仿真過程及分析

顆粒參數見表1，鋪裝機技術參數加工木材規格設定見表2，物料間的相關系數見表3。為了仿真后處理顯示區分均勻度，設置的4 種不同顆粒大小見表4。

表1 顆粒參數Tab.1 Particle parameters

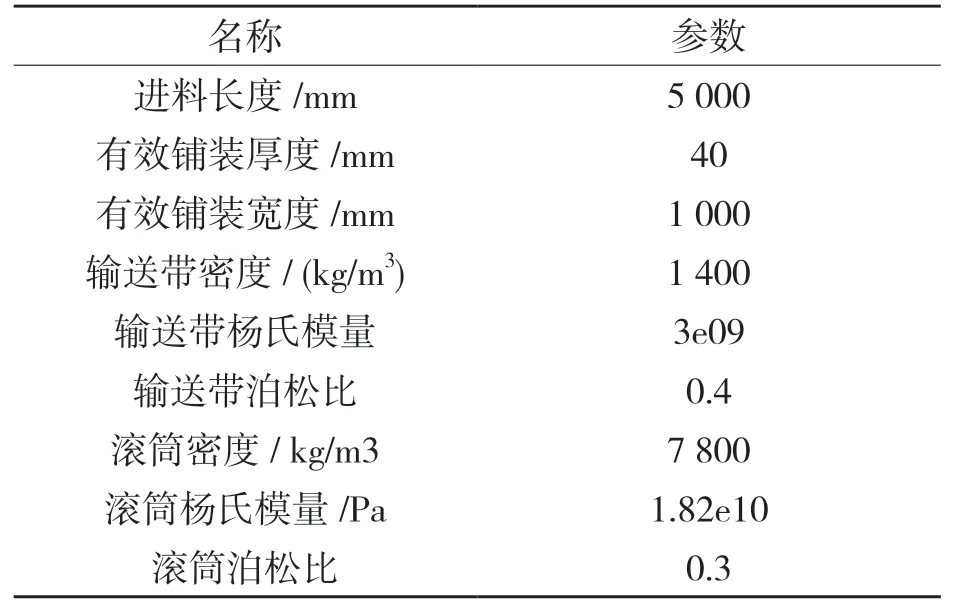
表2 木束鋪裝機技術參數Tab.2 Technical parameters of wood beam paving machine

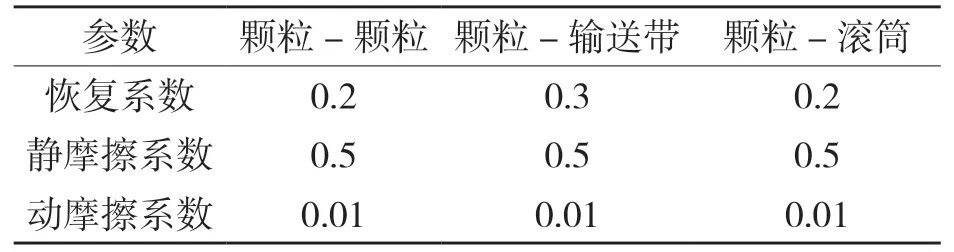
表3 顆粒接觸屬性參數Tab.3 Particle contact attribute parameters

表4 4 種大小顆粒Tab.4 Four sizes of particles

3.1 建立仿真簡化模型與均勻度評價方法

3.1.1 建立仿真簡化模型

為了能更加清晰直觀地模擬鋪料及輸送過程，運用三維建模軟件建立輸送帶、葉片式滾筒、機架等關鍵部件的簡化模型，并導入離散元軟件中進行仿真分析，如圖4 所示。

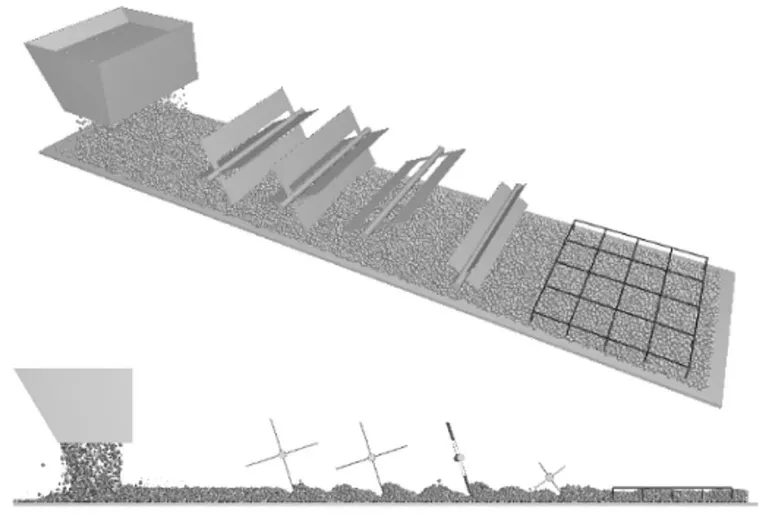
圖4 離散仿真模型Fig.4 Discrete simulation model

3.1.2 均勻度評價方法

設置顆粒固定運動區域，顆粒下落運動速度、輸送帶傳輸速度、滾筒旋轉速度見表5。選取6 s仿真時間，剛好物料都鋪滿輸出端區域。通過在輸出端固定位置設定1.0 m×0.8 m×0.1 m 的網格空間，劃分4×4×1 共16 個一樣大的立方體網格，分別統計每個網格里不同大小顆粒數量的比例，設定一個網格內顆粒數大于400 為有效數據，導出仿真數據并做相應處理，統計均勻度z。由于是4 種大小顆粒混合，只需分別測定不同結構參數下其中一種顆粒的離散系數（采用標準差與平均值的比值）即可衡量鋪料的均勻度（以6 mm顆粒為例）。在網格區域內取k 組數據樣本i，6 mm 顆粒數量為ni，總顆粒數為Ni，則該顆粒所占比例ri為

表5 部件運動參數Tab.5 Component movement parameters

3.2 滾筒安裝高度對鋪料質量的影響

原4 個滾筒之間距離為600 mm，滾筒1，2，4 葉片數量為4，滾筒3 為單葉片。改變滾筒安裝高度，也即改變輸送帶與葉片底端最小距離，滾筒4 安裝高度不變，木料通過壓實滾筒厚度不變，保持為35 mm，其余滾筒高度可調。采用單一變量法，壓實滾筒模型省略，分別改變滾筒1，2，3 葉片底端與輸送帶最小距離都分別為50，60，70 mm。仿真過程如圖5 所示。導出每個網格下4 種顆粒數據，分析計算6 mm 顆粒的離散系數，如圖6 所示，分析可得3 種滾筒安裝高度過高，離散系數都相應變大，均勻度變低。可見，在同時50 mm近距離安裝高度下，離散系數E=0.269 0，均勻度提升，鋪料效果較好。

圖5 鋪料過程仿真Fig.5 Simulation of paving process

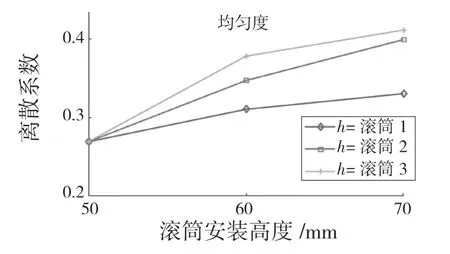
圖6 不同滾筒安裝高度下離散系數Fig.6 Dispersion coefficients under different drum installation heights

3.3 滾筒間的間隔對鋪料質量的影響

在原滾筒安裝高度與葉片數量不變情況下，改變滾筒之間距離單一變量，設定滾筒1，2，3，4 之間的距離分別為600，700，800 mm。統計離散系數可得不同滾筒間間隔為700 mm 時，離散系數最小；E=0.141 2，均勻度較好；間隔過大或過小離散系數會增大，鋪料效果會變差。不同間隔下離散系數變化如圖7 所示。

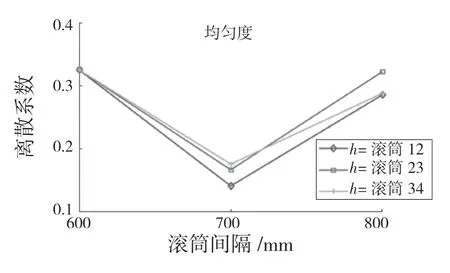
圖7 不同滾筒間間隔下離散系數Fig.7 Dispersion coefficient under different intervals between rollers

3.4 滾筒葉片的數量對鋪料質量的影響

滾筒3 為單葉片，故葉片數量不變。在原滾筒安裝高度與滾筒間間隔不變情況下，改變單一變量，分別同時改變滾筒1，2，4 的葉片數量為3 片，4 片，5 片，統計離散系數可得所有滾筒同時為4 葉片時，E=0.269 0，鋪料均勻度更好。由于葉片自身結構原因，葉片數過多或過少會降低鋪料效果。不同葉片數的離散系數變化如圖8 所示。

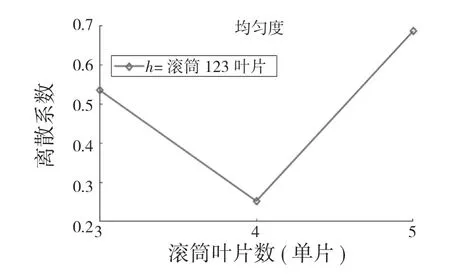
圖8 不同滾筒葉片數下離散系數Fig.8 Discrete coefficients under different number of drum blades

3.5 多因素綜合下的鋪料效果

選取以上3 種影響因素中鋪料效果最好的結構參數綜合仿真，即滾筒安裝高度=50 mm，滾筒間間隔=700 mm，葉片數=4 片時，離散系數E=0.141 2，可知該值剛好比其它結構參數下低。因此可知，基于設定參數下，各低離散系數下結構參數組合仿真后能得到更低的離散系數，即更好的鋪料效果。

4 結論

（1）為了解決鋪料過程木料的表面缺陷和內部錯亂問題，改善平整性與均勻性，利用離散元仿真軟件對鋪料機做結構優化，確定影響鋪料質量的關鍵因素有滾筒安裝高度、滾筒間的間隔、滾筒葉片的數量。

（2）對鋪料機及不同參數下的結構進行仿真。結果表明，不同因素的平均離散系數分別為=0.331 3，=0.261 6，=0.490 7，故對鋪料質量的影響大小關系為滾筒間的間隔>滾筒安裝高度>滾筒葉片的數量，改變結構參數以分析較好的鋪料效果，為后續模壓成型提供保障。同時，基于設定參數下，各低離散系數因素組合就能得到好的鋪料效果。

（3）由于采用了鏈傳動機構，鋪料時存在沖擊和振動，限于結構分析方向，可延伸探討振動設施對鋪料效果影響，如輸送帶下加入振動棒，通過優化頻率幅值，來達到對木質散料的抖動均勻，有待后續進一步分析驗證。