鋰離子電池極耳分布對電極應力的影響
馬德正,李培超
(201620 上海市 上海工程技術大學 機械與汽車工程學院)
0 引言
鋰離子電池是一種新型高效綠色的可再充電電池,因具有能量密度高、工作電壓高、自放電率低、無記憶效應的優點被廣泛應用[1-2]。在電池充放電過程中,鋰離子嵌入/脫出以及溫度的變化將會導致電極內部產生應力,應力過大將導致電極活性材料剝落、解體和SEI 膜的增加[3-5],進而導致電池循環壽命下降和容量的損失[6-7]。溫度對電池安全性和循環壽命的影響至關重要,因此電池結構優化設計及其熱管理極為關鍵[8]。
電池極耳在電池內部主要起到連接集流器的作用,很多學者對極耳結構進行了分析研究。陳宏[9]等通過實驗方法研究了高速放電條件下,不同極耳位置分布和幾何尺寸對電池的影響,并最終對其尺寸提出優化;莫治波[10]等對圓柱形鋰離子電池極耳位置進行了研究,發現將極耳由側邊改到中間能有效降低電池內阻;王安安[11]等通過數值模擬研究了電池極耳在雙側分布和單側分布下對軟包電池的電芯熱行為的影響;龍梅和唐有根[12]通過對不同尺寸和位置分布的極耳進行實驗研究,發現極耳寬度和厚度越大越有益于電池的高速率放電;陳才星[8]等建立了鋰離子電池的三維分層結構模型,分析了電池溫度場的分布特征,同時對極耳尺寸進行了優化,降低了電池放電產熱;黃偉國[13]等通過對鉛炭電池的極耳在同側和對側排布方式下的充電析氫量、放電曲線和電池容量的實驗研究,發現極耳在對側布置下電池放電電壓和循環壽命會更高。以上工作皆在分析極耳排布對電池電化學和熱性能的影響,但均未考慮電極極耳對電極應力的影響。
本文建立了一個三維鋰離子電池電化學-熱-力耦合模型對電極內部電流場、溫度場和應力場進行求解,分析相同放電倍率時正負極耳在不同排布方式下對電極應力的影響,同時對極耳尺寸和材料屬性(楊氏模量和泊松比)進行了參數分析,研究其對電池內部電極應力的影響。
1 數學模型
模型選取容量為90 A·h的磷酸鐵鋰/石墨電池內部最小單元為研究對象,如圖1 所示。圖1(b)中從左至右依次為負極集流器(Cu)、負極材料、隔膜、正極材料和正極集流器(Al)。其中,電池寬度Wcell=12.69 cm,高度Hcell=19.42 cm。負極集流器厚度Lcu=3 μm,負極厚度Lneg=63 μm,隔膜厚度Lsep=16 μm,正極厚度Lpos=86.5 μm。正極集流器厚度LAl=7.5 μm;正極極耳寬Wpos=9.55 cm,高度Hpos=1.5 cm,中心與電池中心距離dpos=0。負極極耳寬度Wneg=4.55 cm,高度Hneg=1.5 cm,中心與電池中心距離dneg=3.175 cm。單元厚度Lcell=0.176 mm。
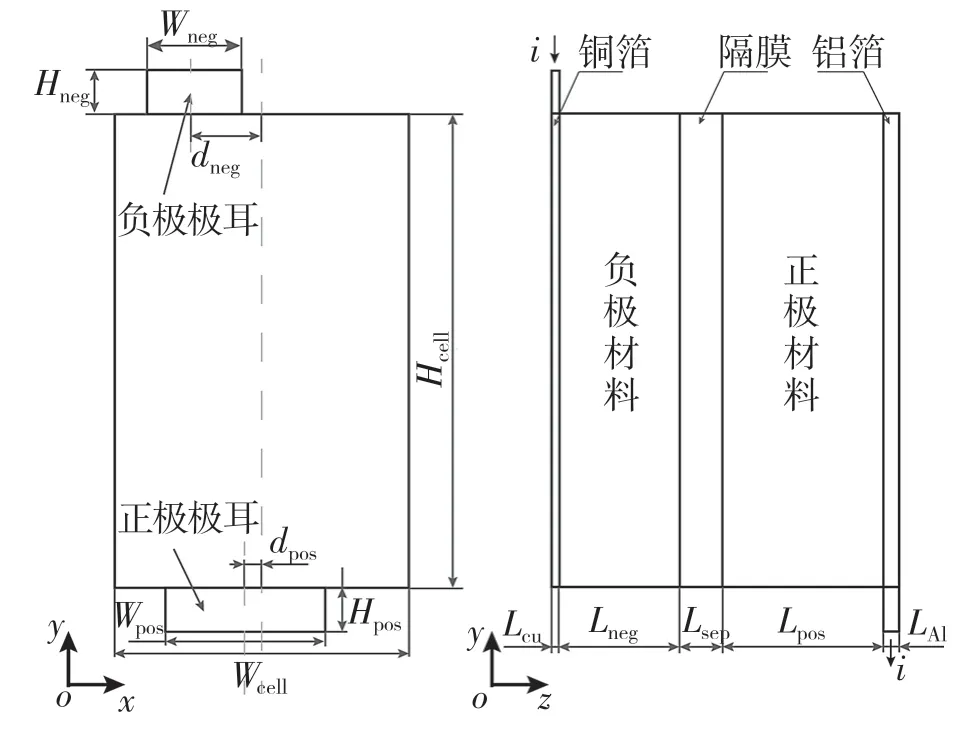
圖1 模型原理圖Fig.1 Schematic diagram of the model
1.1 控制方程
(1)電荷守恒
電池內部電荷守恒包含電子電荷守恒與離子電荷守恒。電極活性材料與集流器內的電子電荷守恒遵循歐姆定律,如式(1)所示。
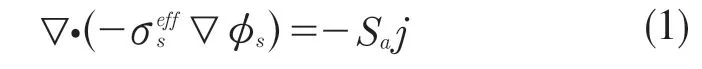
電解液內部離子電荷守恒方程,如式(2)所示。

(2)質量守恒
電極活性材料球型顆粒內鋰的質量守恒遵循菲克第二定律,如式(3)所示。

式中:cs——鋰濃度;——有效擴散系數;r ——顆粒內徑向坐標。
鋰離子在電解液中的傳遞遵循質量守恒定律,如式(4)所示。
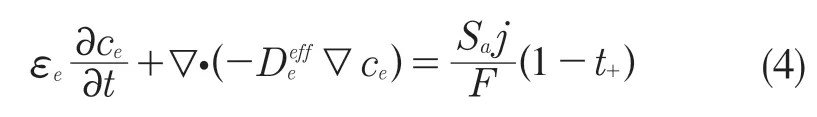
(3)電化學動力學
電極活性材料表面局部電流密度由Bulter-Volmer 方程計算得到,如式(5)所示。
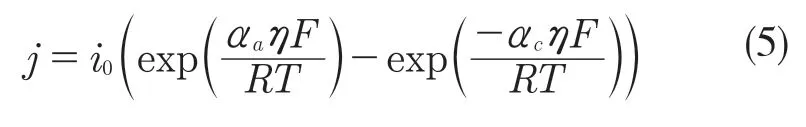
式中:αa,αc——陽極和陰極的傳遞系數;i0——交換電流密度,如式(6)所示。

式中:ka——陽極反應速率常數;kc——陰極反應速率常數;cs,max——活性材料最大鋰濃度;cs,surf——活性材料顆粒表面鋰濃度;ce,ref=1 mol/m3電解液參考濃度。
式(5)中過電位η公式如式(7)所示。
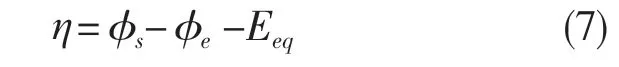
式中:Eeq——電極開路電勢,其值由參考溫度Tref=298.15 K 下的參考電勢Eeq,ref和平衡電位溫度倒數dEeq/dT 計算得到,如式(8)所示。
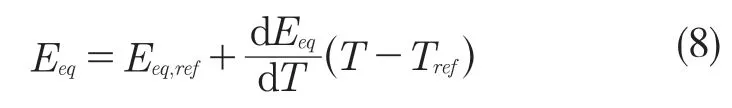
Eeq,ref和dEeq/dT 隨充電狀態(SOC)的變化曲線[8]分別如圖2(a)和圖2(b)所示。
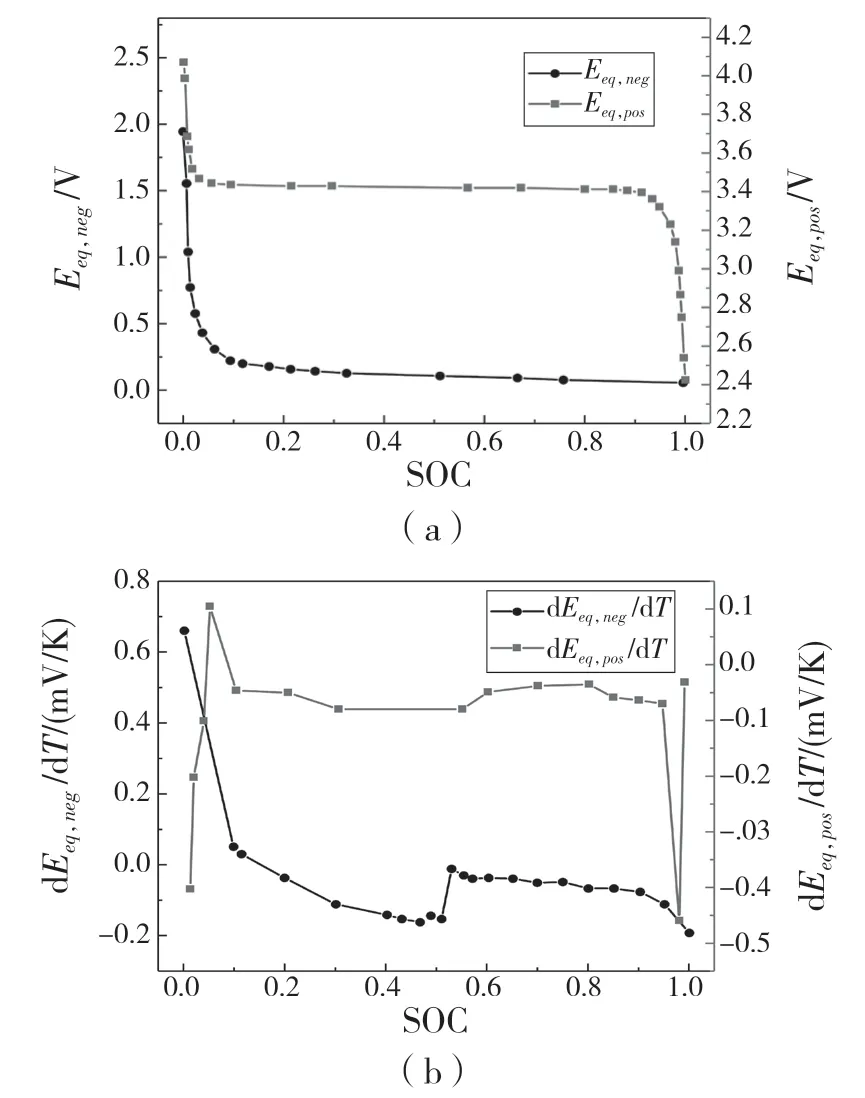
圖2 電極平衡電位和熵變Fig.2 Electrode equilibrium potential and entropy change
(4)能量守恒
考慮電極、電解液和集流器內部產熱,模型內部能量守恒控制方程如式(9)所示。

式中:ρ——密度;CP——比熱容;KT——熱導率。等式右側分別表示可逆熵熱、極化熱、電子歐姆熱和離子歐姆熱。本文中不考慮電池模型同環境間的熱交換。
(5)體積應變
電極活性材料內部總應變εij由機械應變、熱應變=βΔTδij和擴散誘導應變=ΩΔcδij/3共同決定,如式(10)所示。

式中:β——熱膨脹系數;Ω——粒子摩爾體積。
2 模型參數和驗證
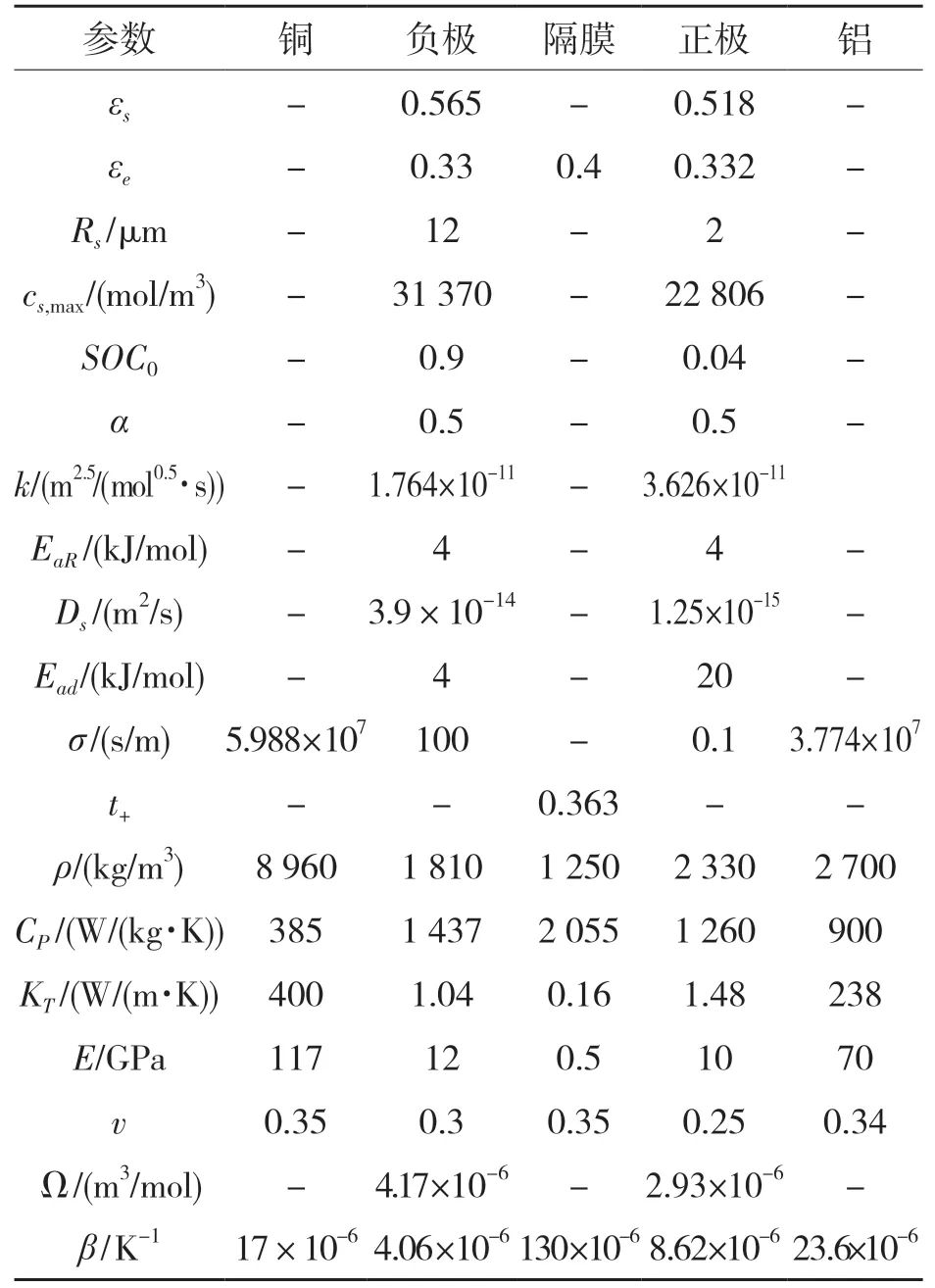
表1 模型參數Tab.1 Model parameters
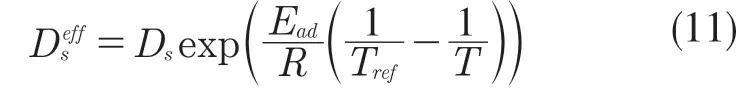
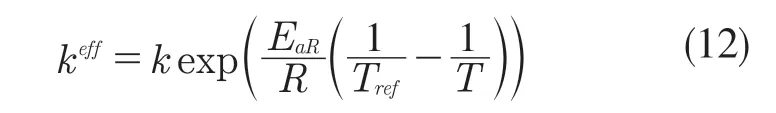
式中:Ead,EaR——擴散活化能和反應活化能。

圖3(a)和圖3(b)分別為數值求解到的電池電壓和溫度隨時間變化的結果與實驗數據的對比。由圖可知,本文結果與實驗結果相接近,從而驗證了本文所建立模型的可靠性。
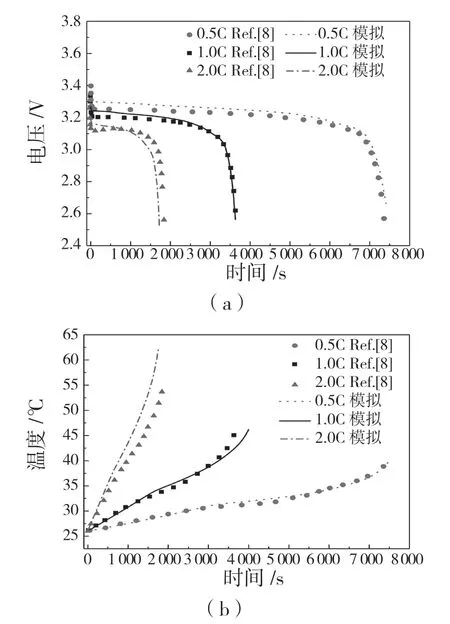
圖3 電壓和溫度曲線與實驗數據[8]對比Fig.3 Comparison of voltage and temperature curves with experimental data[8]
3 結果和討論
3.1 極耳分布影響
為分析極耳位置分布對電池性能的影響,特將正極耳設置為與負極耳相同的尺寸。本文分別考慮A,B,C,D,E,F 六種極耳分布方式,如圖4 所示。通過使用數值軟件求解得到電極內部鋰離子濃度和溫度的分布。正極活性材料表面在1C 放電條件下放電至t=3 000 s 時的鋰濃度和溫度分布分別如圖5、圖6 所示。
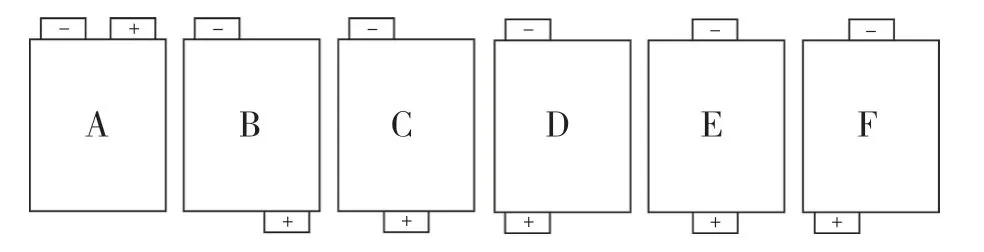
圖4 極耳排布方式Fig.4 Arrangement of the tab
由圖5、圖6 可知,正極材料在靠近負極耳側反應更強,靠近負極耳的區域相比其它區域溫度更高、鋰離子嵌入量也更多;靠近正極耳區域處的反應稍弱,相比靠近負極耳區域的鋰濃度和溫度也略低。同時,發現靠近極耳側的電極區域電化學反應更強。當t=3 000 s 極耳處于A,B,C,D,E,F 位置時,正極電極表面最大濃度差分別為333.5,195.2,189.3,199.9,158.8,171.1 mol/m3,正極電極表面溫度差分別為0.439,0.177,0.171,0.184,0.103,0.114 K。結果發現,極耳采取對側分布可使電池內部電化學反應更均勻。在對側排布中,正負極耳均處于中間位置時,正極表面濃度差和溫度差更小,即極耳在這種分布狀態下電池電化學反應更均勻且產生熱更低。

圖5 正極表面濃度分布Fig.5 Surface concentration distribution of the cathode

圖6 正極表面溫度分布Fig.6 Surface temperature distribution of the cathode
圖7 為1C 放電條件下放電至t=3 000 s 時正極活性材料表面von Mises 應力分布。由圖7 可知,von Mises 應力最大值在極耳同側排布時的最大,當極耳處于對側排布時von Mises 最大值會降低。同時,當負極極耳位于中間位置時,即在E 和F排布方式下von Mises 最大值較小。6 種極耳分布下,von Mises 應力差值分別為1.909,1.323 8,1.113,1.217 9,0.985 5,1.081 6 MPa,極耳在E排布下正極表面von Mises 應力差值更小。當極耳在E 排布下以2C 放電速率放電至t=1 500 s 時正極表面von Mises 應力分布如圖8 所示,可知當放電速率增加時正極表面von Mises應力將增大。

圖7 正極表面von Mises 分布Fig.7 Surface von Mises stress distribution of the cathode

圖8 正極表面von Mises 分布Fig.8 Surface von Mises stress distribution of the cathode
3.2 極耳尺寸影響
以極耳在E 方式排布為例,分析極耳的存在對正極電極表面應力的影響。圖9(a)、圖9(b)分別表示極耳Hpos=0 和Hpos=1.5 cm 時正極表面von Mises 應力分布。對比可知,極耳的存在會導致電極表面的最大von Mises 應力增加,且最大von Mises 應力將出現在靠近正極極耳區域。這是由于此處電極活性材料在鋰離子嵌入和溫度變化所導致的體積應變受到極耳的限制,進而造成在靠近極耳區域存在比較大的von Mises 應力。圖9(b)—圖9(d)為正極耳寬度對正極電極表面應力的影響,圖9(b)—圖9(d)對應的極耳寬度分別為Wpos,1.5Wpos,2.5Wpos。結果發現,極耳寬度的增加會導致電極表面應力的增大。

圖9 極耳尺寸對電極應力影響Fig.9 Effect of tab size on electrode stress
3.3 極耳材料屬性的影響
圖10 為正極表面在不同楊氏模量和泊松比下的von Mises 應力分布,其中,圖10(a)對應,E=70 GPa,v=0.34;圖10(b)對應 E=20 GPa,v=0.34;圖10(c)對應E=20 GPa,v=0.20。由圖可知,隨著正極極耳楊氏模量的降低,極耳對正極材料的變形限制作用減弱,從而電極表面最大von Mises 應力值降低。隨著極耳材料泊松比的減小,正極材料表面最大von Mises 應力值將會增加,因此極耳材料應盡可能選用楊氏模量低且泊松比較大的材料。
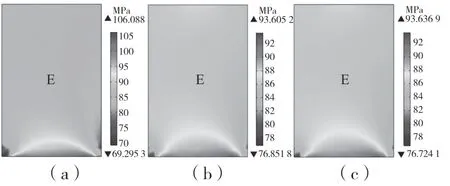
圖10 楊氏模量和泊松比對電極應力影響Fig.10 Effect of Young's modulus and Poisson's ratio on electrode stress
4 結論
本文建立了鋰離子電池三維電化學-熱-力耦合模型,通過與實驗數據的對比驗證了模型的可靠性,并通過該模型對極耳分布、尺寸和材料屬性進行分析。結果如下:
(1)通過對正負極耳在6 種排布方式下的數值計算結果可知,當正負極耳處于中間位置(E排布)時電極電化學反應會更均勻,電極內鋰濃度會更加均勻的同時產熱會更低。負極耳居中放置能有效降低電極表面最大von Mises 應力值。
(2)對極耳尺寸的分析可知,極耳結構的存在會導致正極電極表面最大von Mises 應力從靠近負極耳的區域轉移動到靠近正極耳的區域,且電極表面的最大von Mises 應力值將增大。同時當極耳寬度增加時也會導致電極表面的最大von Mises 應力值的增加。
(3)極耳結構有效楊氏模量的減小可使電極表面最大von Mises 應力值降低,泊松比的減小會導致電極表面最大von Mises 應力值的增加,因此在極耳選材應盡量選用楊氏模量低且泊松比較大的材料。

