基于虛擬矢量的五相永磁同步電動機直接轉矩容錯控制

秦翌菲，王愛元，卜玉杭

（上海電機學院電氣學院，上海201306）

五相永磁同步電動機（Five Phase Permanent Magnet Synchronous Motor，FP-PMSM）屬于多相電機，含有多個自由度，在發生缺相故障時無需額外的設備即可實現容錯運行。具有該優勢的多相電機在航空航天、船舶驅動、新能源汽車等場合得到廣泛的應用［1-3］。

直接轉矩控制（Direct Torque Control，DTC）技術最初應用在異步電動機上，直到1996年才研究出真正意義上可應用在永磁同步電動機（Permanent Magnet Synchronous Motor，PMSM）上的DTC技術［4-7］。DTC技術具有結構簡單，不依賴電機參數等優點，在多相電機領域得到廣泛的應用［8-9］。鄧威等［10］提出了一種基于虛擬電壓矢量的三電平逆變器DTC技術，提高了電壓利用率，減少了轉矩脈動。蘇丹丹等［11］在傳統DTC技術的基礎上引入零矢量，對模型預測算法進行優化，減少了預測計算量與轉矩脈動。朱亮等［12］基于滑模算法，將系統的傳統比例積分（Proportional Integra，PI）模塊替換為模糊PI模塊，起到減小轉矩脈動和增強魯棒性的作用。以上文獻均表明DTC算法對轉矩控制的有效性，但其均應用在三相系統上，體現不出對多相系統的有效性。

在多相電機驅動系統中，DTC技術利用多相電機具有多個自由度的特點，結合相應的容錯控制方法得到廣泛的關注。武雪松等［13］采用基于虛擬電壓矢量集的DTC算法，有效地減少了電流諧波含量，但虛擬矢量構建個數較多，采用預測控制選取最優矢量會造成計算量過大。周揚忠等［14］重構變換矩陣獲得FP-PMSM缺相模型，構建虛擬磁鏈等虛擬變量設計最優開關表，實現故障后的容錯控制，但開關表選用矢量較多，選擇最優矢量較復雜。

本文針對缺相后系統轉矩脈動偏大及上述文獻存在的矢量選用復雜問題，提出了一種基于虛擬電壓矢量的DTC容錯控制方法。構建缺相狀態下的FP-PMSM數學模型，根據缺相后電壓矢量分布特點，進行矢量重構獲得虛擬電壓矢量。構建的虛擬電壓矢量數量少、選擇簡單，能有效地抑制缺相后x-y子空間諧波分量，抑制轉矩脈動，取得了良好的控制性能。

1 FP-PMSM缺相數學模型

1.1 FP-PMSM缺一相數學模型

FP-PMSM系統發生缺相故障時，系統的數學模型必然會隨之發生相應的改變。仿照正常狀態下數學模型的建立方法，建立發生故障后的缺相變換矩陣［15］。

當系統發生缺相故障時，以A相開路為例，對正常工作狀態下的變換矩陣去掉A相對應元素，原5階對稱矩陣變換為4階不對稱矩陣如下：

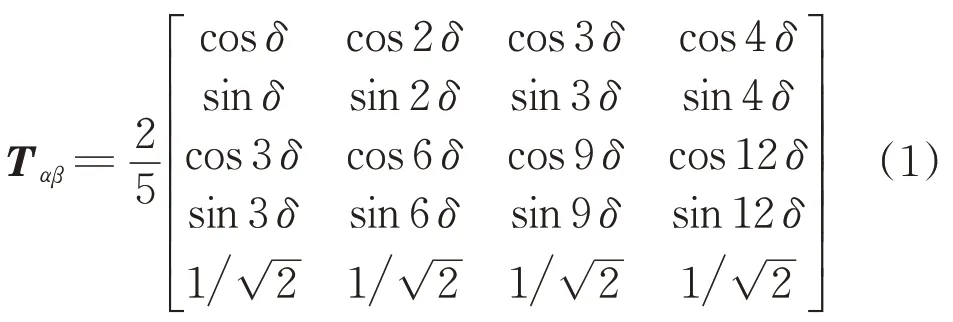
式中：δ=2π5

對變換后的矩陣分析可知，矩陣中第1與第3行不再和第5行正交，故對矩陣進行校正，使發生故障后的變換矩陣繼續保持對稱。在第1行加入校正系數x，刪去第3行，使第1與第5行正交。經求解可得x=-1，則校正后的矩陣為

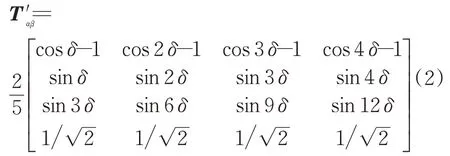
在FP-PMSM系統中，各相電壓、電流和磁鏈分量可表示為Ui、Ii和ψi（自然坐標系中i=A，B，C，D，E；靜止坐標系中i=α，β，x，y；同步旋轉坐標系中i=d，q）。當發生A相缺相故障時，系統的電壓與磁鏈方程為

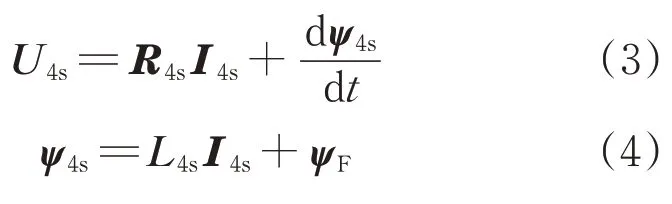
其中，

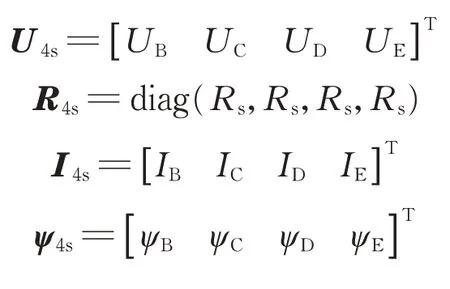
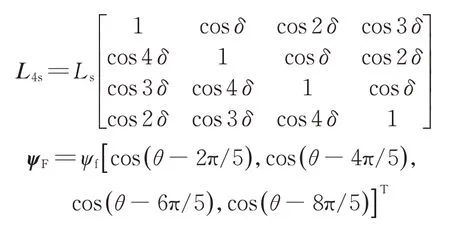
式中：U4s為缺相后的電壓矩陣；R4s為缺相后的電阻矩陣；Rs為定子電阻值；I4s為缺相后的電流矩陣；ψ4s為缺相后的磁鏈矩陣；L4s為缺相后的電感矩陣；Ls為電感值；ψF為缺相后的永磁磁鏈矩陣；ψf為永磁磁鏈幅值；θ為電角度。

采用校正后的變換矩陣，將上述各參數變換到α-β靜止坐標系下，有

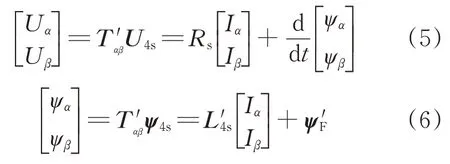
其中，

根據轉矩計算原理，缺相故障后的電磁轉矩為

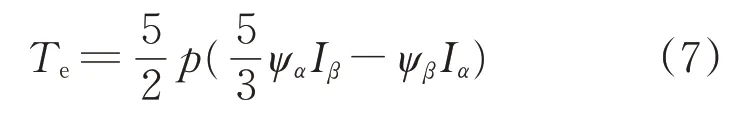
式中：p為轉子極對數。

對比式（7）與未發生故障的轉矩方程可知，發生缺相故障后β軸磁鏈幅值未發生變化，α軸磁鏈幅值減少40%。

1.2 FP-PMSM故障后電壓矢量分布

FP-PMSM發生缺相故障時，以缺A相為例，母線電壓設為Udc，剩余健康相電壓的矩陣形式為

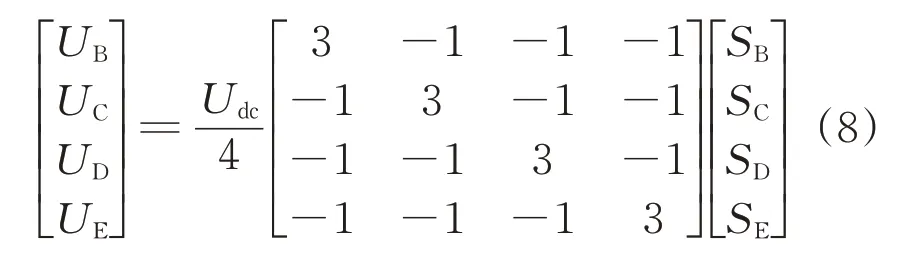
缺相故障下不同開關狀態Si（Si=1或0，i=B，C，D，E）對應不同的電壓矢量。經計算，電壓矢量由正常狀態下的32個減為16個。采用變換矩陣將電壓矢量由自然坐標系變換到靜止坐標系，分布情況如圖1所示。

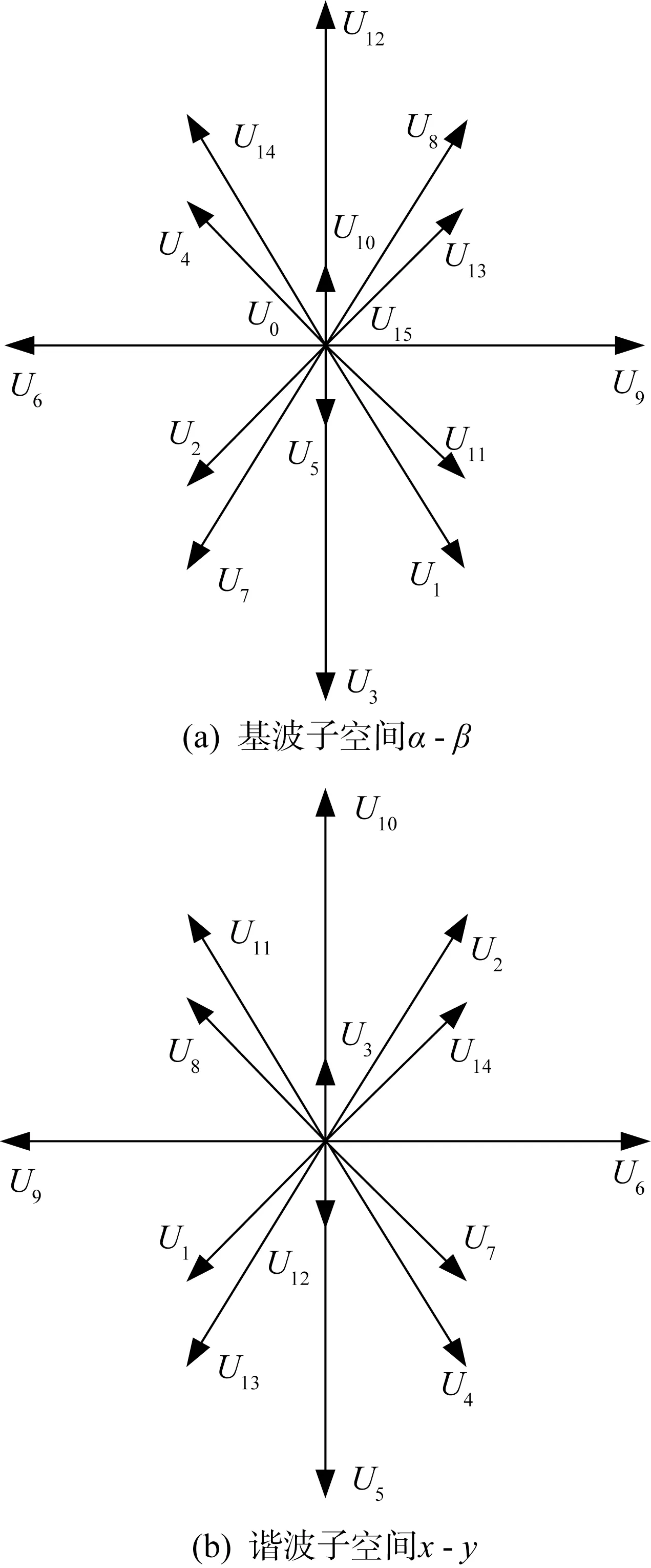
圖1 靜止坐標系下故障后電壓矢量分布

將電壓矢量按幅值大小分類，如表1所示。

表1 故障后電壓矢量幅值

2 直接轉矩容錯控制

2.1 虛擬電壓矢量的構建

考慮到x-y子空間中電壓矢量分量會造成諧波的產生，影響轉矩脈動以及DTC開關表中最優矢量的選取，因此對故障后電壓矢量進行重構。

正常狀態下經變換矩陣變換，A相電流與α-β和x-y子空間電流關系為

當系統發生缺一相故障時，A相電流為零，即IA=0，則

可知，系統的x-y子空間控制3次諧波的分量僅剩y軸分量，故將y軸分量控制為零可抑制3次諧波的影響。當僅考慮x-y子空間y軸分量時，非零電壓矢量分布如圖2所示，圖2中故障后x-y子空間y軸分量幅值見表2。

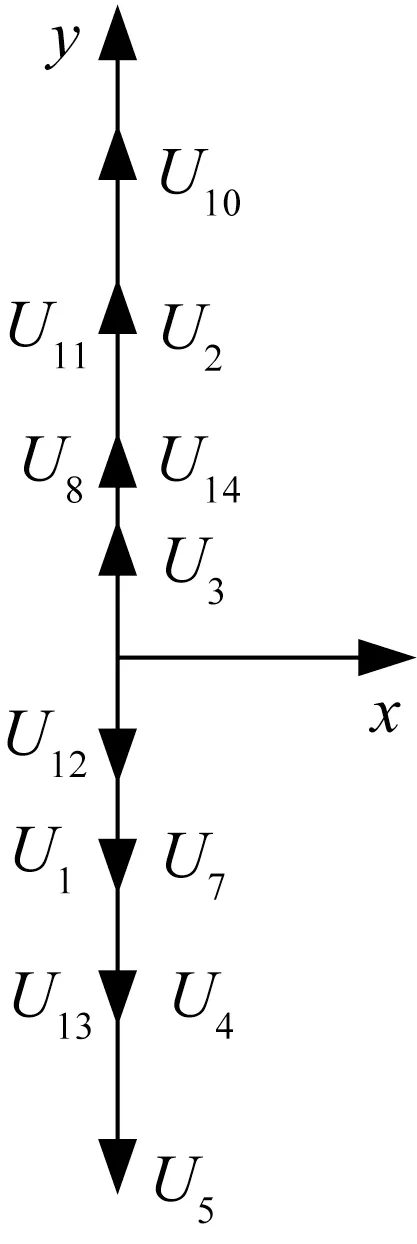
圖2 x-y子空間電壓矢量y軸分量

表2 故障后x-y子空間y軸分量幅值

由圖2和表2可知，有兩種方法可將y軸分量合成為零：①采用幅值相同、方向相反的電壓矢量進行合成；②采用不同幅值、方向相反的電壓矢量，通過V·s平衡原則進行合成。

在方法①中，采用圖2中矢量U1、U8合成，y軸分量合成為零，但在α-β子空間中，矢量U1、U8對轉矩與磁鏈的影響作用呈相反狀態；采用矢量U8、U7進行合成，會出現α-β子空間矢量合成為零的情況，對轉矩與磁鏈無影響作用。因此，采用方法①進行矢量合成不符合要求。

當選用方法②時，采用矢量U8、U13進行合成，y軸分量合成為零，在α-β子空間中矢量U8、U13對轉矩與磁鏈的影響效果相同。因此，選用方法②計算出合適的矢量作用時間ts，使x-y子空間中電壓y軸分量合成為零。

以矢量U8、U13為例，可得

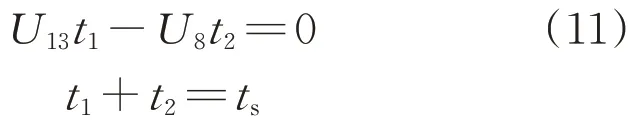
式中：t1為0~ts時刻U13電壓矢量作用時間；t2為0~ts時刻U8電壓矢量作用時間。

經計算可得

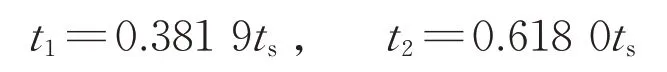
在α-β子空間中，由t1、t2計算出虛擬電壓矢量UV2的幅值為

對14個非零電壓矢量均采用方法②進行合成，將α-β子空間劃分為8個扇區，可得非零虛擬電壓矢量分布圖如圖3所示。

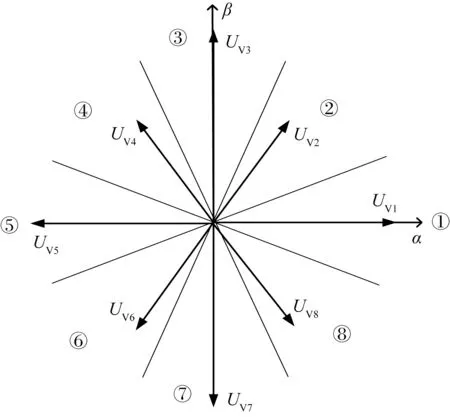
圖3 虛擬電壓矢量分布

2.2 DTC容錯控制原理

按照DTC原理，在同步旋轉坐標系中將d軸與定子磁鏈矢量重合，則ψ4s=ψd，ψq=0。結合式（3）對定子電流進行離散化處理，可得定子電流變化量為

式中：Ts為虛擬電壓矢量作用的時間；Ld、Lq為定子電感；ωe為旋轉角速度。

在上述條件下，由式（3）可知磁鏈在虛擬電壓矢量作用時的變化率，離散化后磁鏈的變化量為

分析上述各式，在采樣時間內，磁鏈的變化量主要取決于所選用的虛擬電壓矢量。

FP-PMSM的電磁轉矩以另一種方式表示為

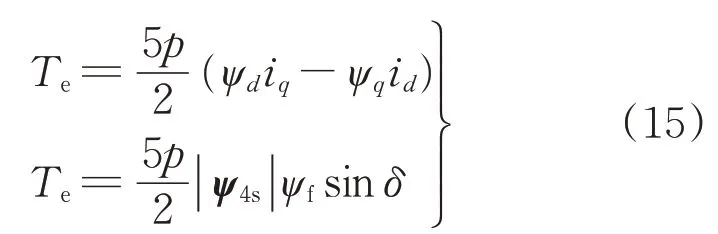
由式（15）可知，轉矩的變化量ΔTe，按定子電流的變化量表示為

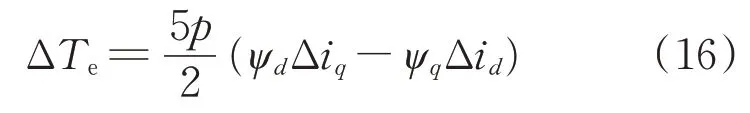
結合上述條件可將式（16）改寫為

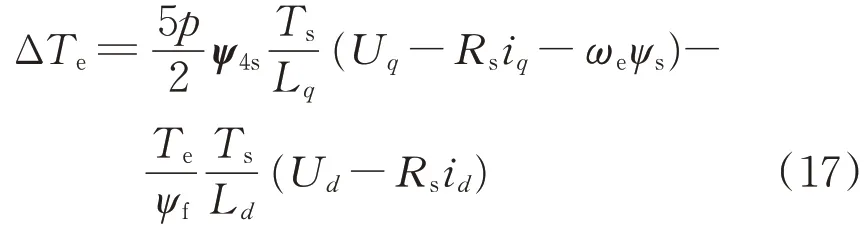
結合式（14），將式（17）表示為：ΔTe=ΔTe1+ΔTe2。可得

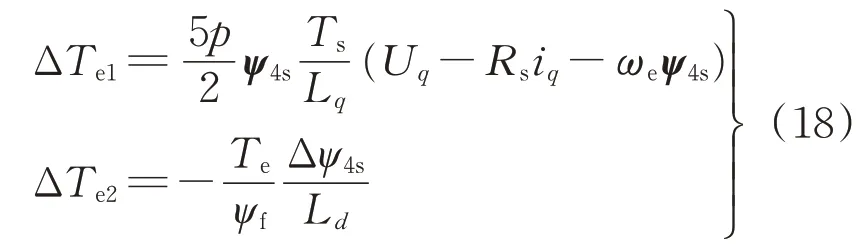
由式（18）可知，當施加不同的虛擬電壓矢量時，電磁轉矩的變化量ΔTe，不僅取決于虛擬電壓矢量及虛擬電壓矢量的作用時間Ts，還與定子電流有關。

圖4為磁鏈位于第1扇區時，虛擬電壓矢量對磁鏈的影響。在第1扇區中定義虛擬電壓矢量UV1為0°分界線，將第1扇區分為上扇區與下扇區。分析磁鏈位于不同的位置時，不同虛擬電壓矢量的影響，作為選取最優電壓矢量的條件。

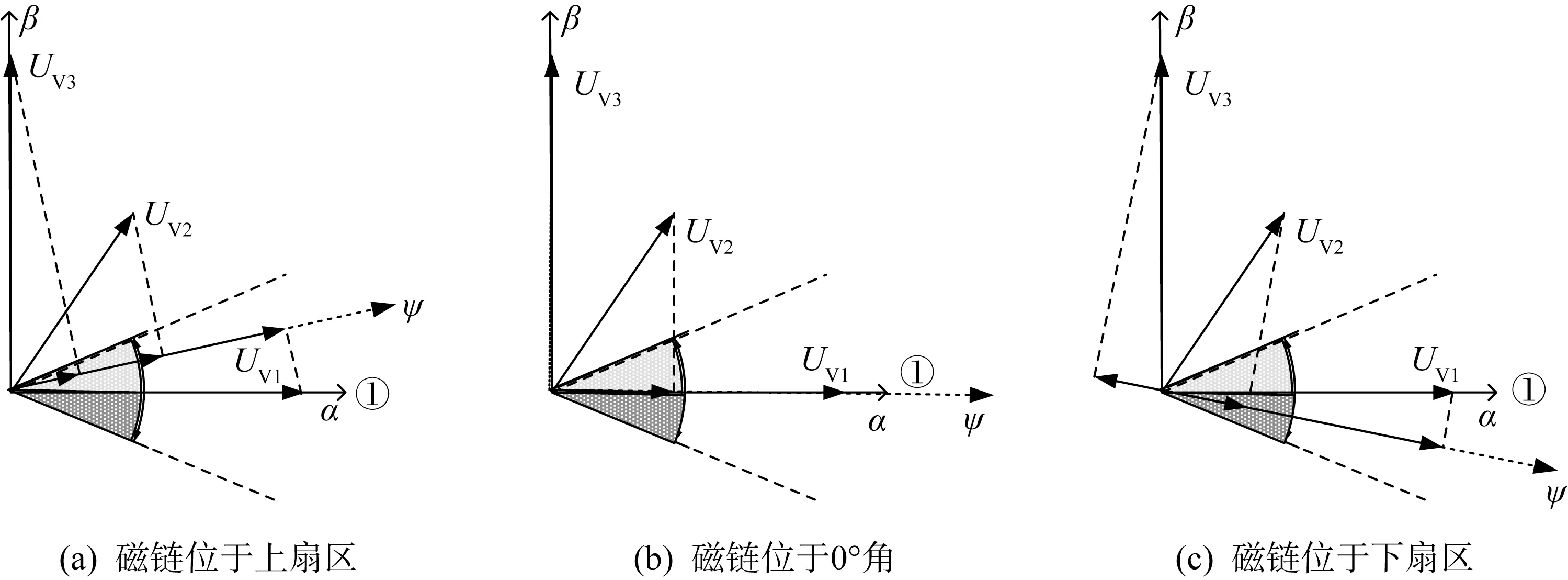
圖4 虛擬電壓矢量對磁鏈的影響

以UV1、UV2、UV3為例，在圖4（a）中，當磁鏈位于第1扇區的上扇區時，各虛擬電壓矢量對磁鏈的影響均為正向，以UV1的影響為主；在圖4（b）中，磁鏈位于0°時，UV3無任何影響作用，UV1為主要影響；在圖4（c）中，UV3對下扇區磁鏈的影響為負向，UV1仍為主要影響。因此，當磁鏈位于第1扇區時，UV1處于不同的位置，有不同的影響作用，但整體上對磁鏈影響作用是正向。

將上述分析作為基本分析法，對磁鏈位于第1扇區任意位置的虛擬電壓矢量進行分析，虛擬電壓矢量對磁鏈的影響如圖5所示。

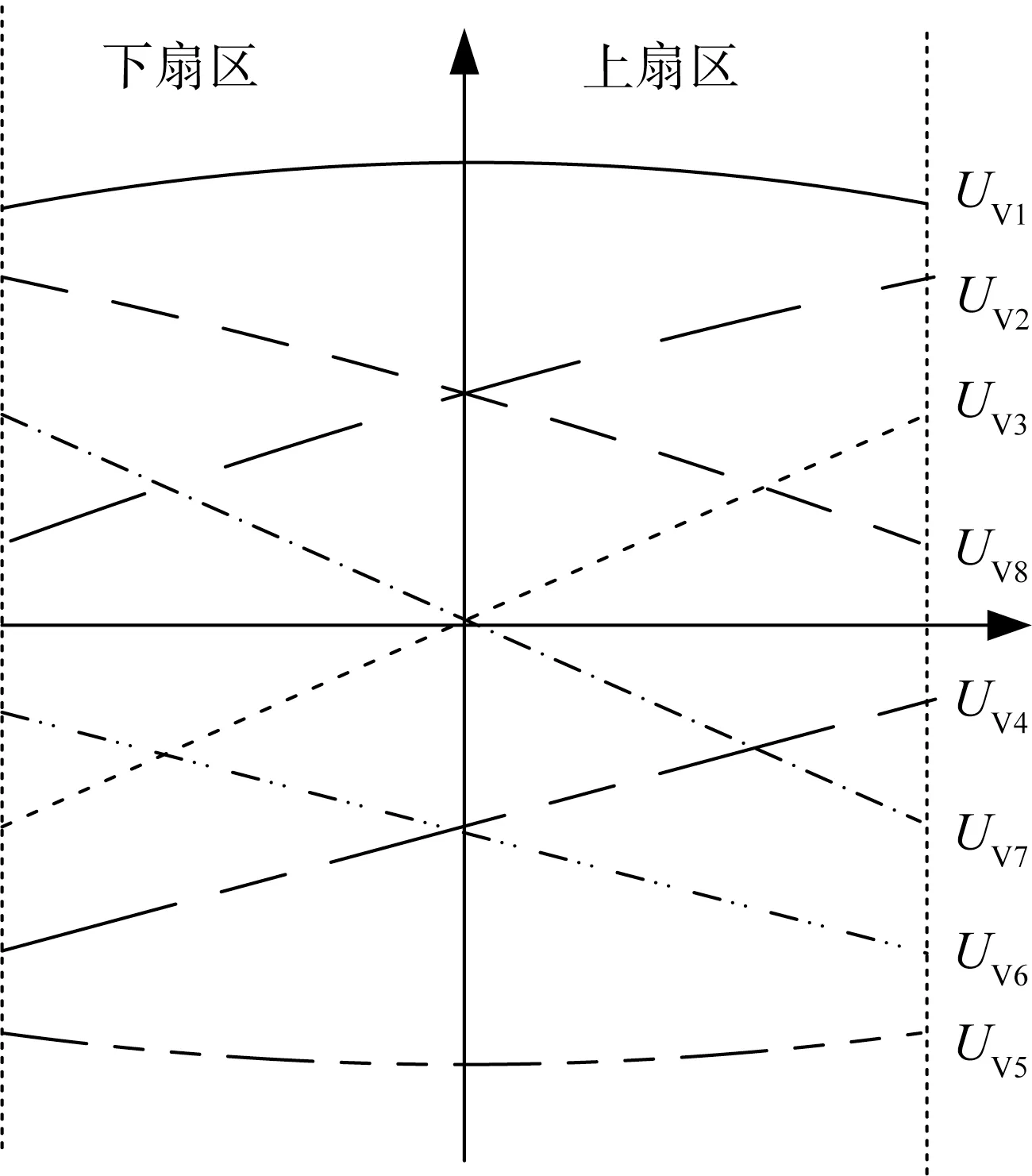
圖5 虛擬電壓矢量對磁鏈的影響

轉矩的分析與正常狀態下類似。結合式（18）可知，在第1扇區選用虛擬電壓矢量UV1，轉矩的影響是負向，UV2與UV3在上扇區與下扇區為正向影響。

根據以上分析，以第1扇區為例，FP-PMSM缺一相虛擬矢量開關表如表3所示。

表3 基于虛擬矢量的直接轉矩開關表

3 仿真與分析

為驗證本文控制方法的有效性，在Simulink仿真環境中搭建缺一相FP-PMSM模型。結合本文控制方法，構建FP-PMSM缺一相容錯控制系統。系統框圖如圖6所示，采用經典DTC控制結構，磁鏈、轉矩雙滯環控制。FP-PMSM參數如表4所示。

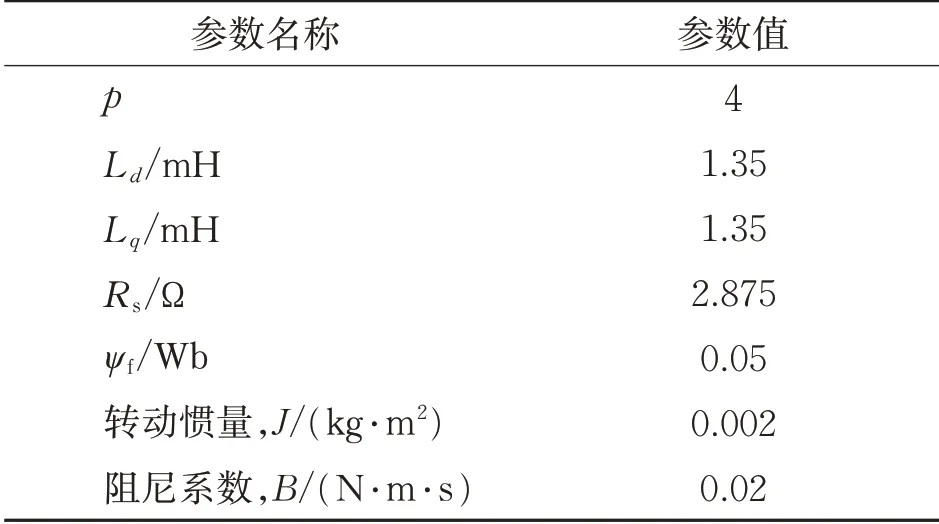
表4 FP-PMSM參數

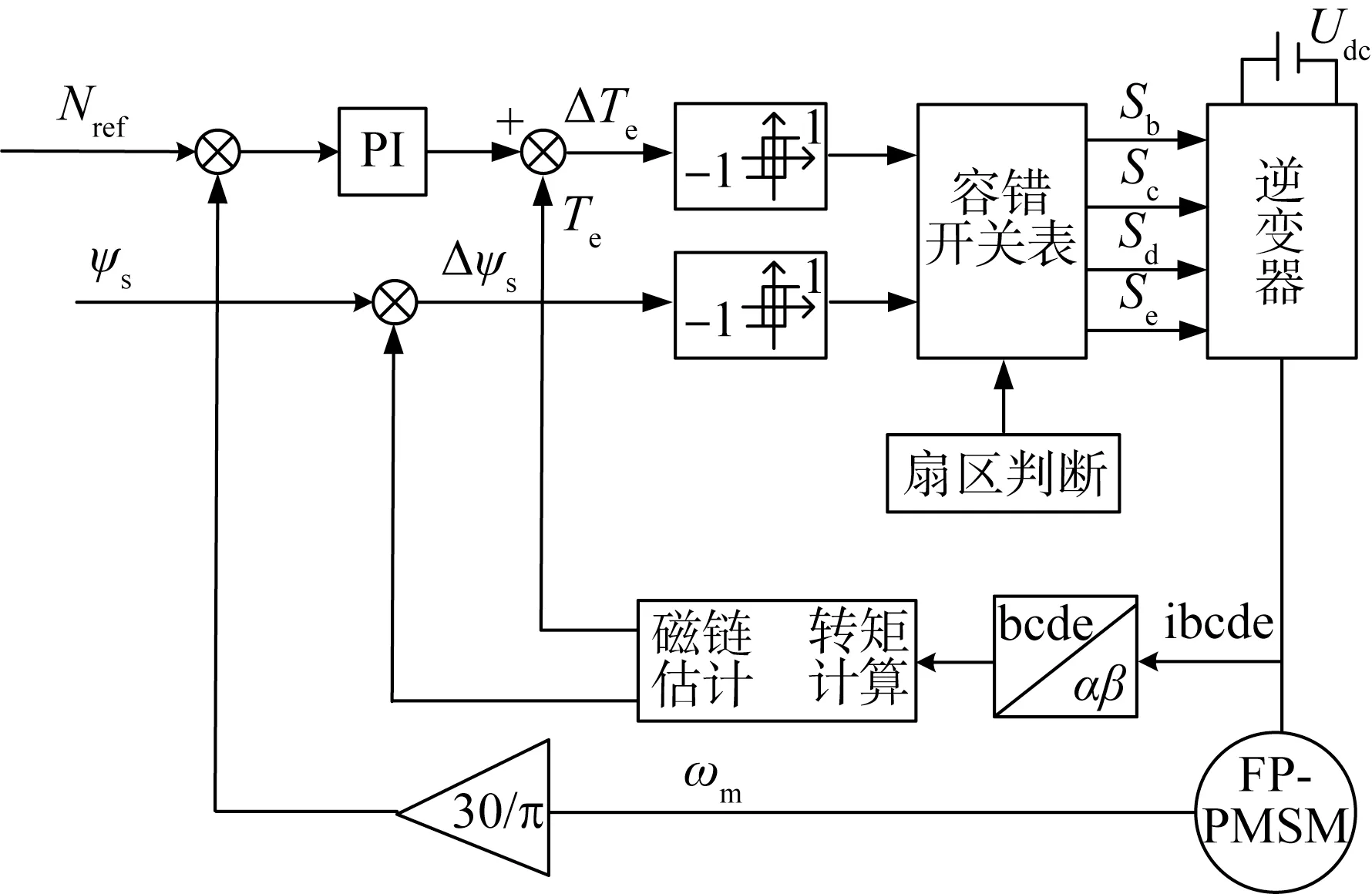
圖6 基于虛擬電壓矢量的直接轉矩容錯控制系統框圖

系統部分仿真參數設置為：母線電壓Udc=311V，仿真時間0.1 s，參考轉速Nref=1000 r min，初始負載轉矩為7 N·m。系統采用傳統開關表控制的正常狀態運行，在0.04 s時模擬出現缺A相故障，在0.07 s時投入基于虛擬電壓矢量的DTC容錯控制方法。經仿真可得電流、轉矩和轉速的對比波形如圖7所示。

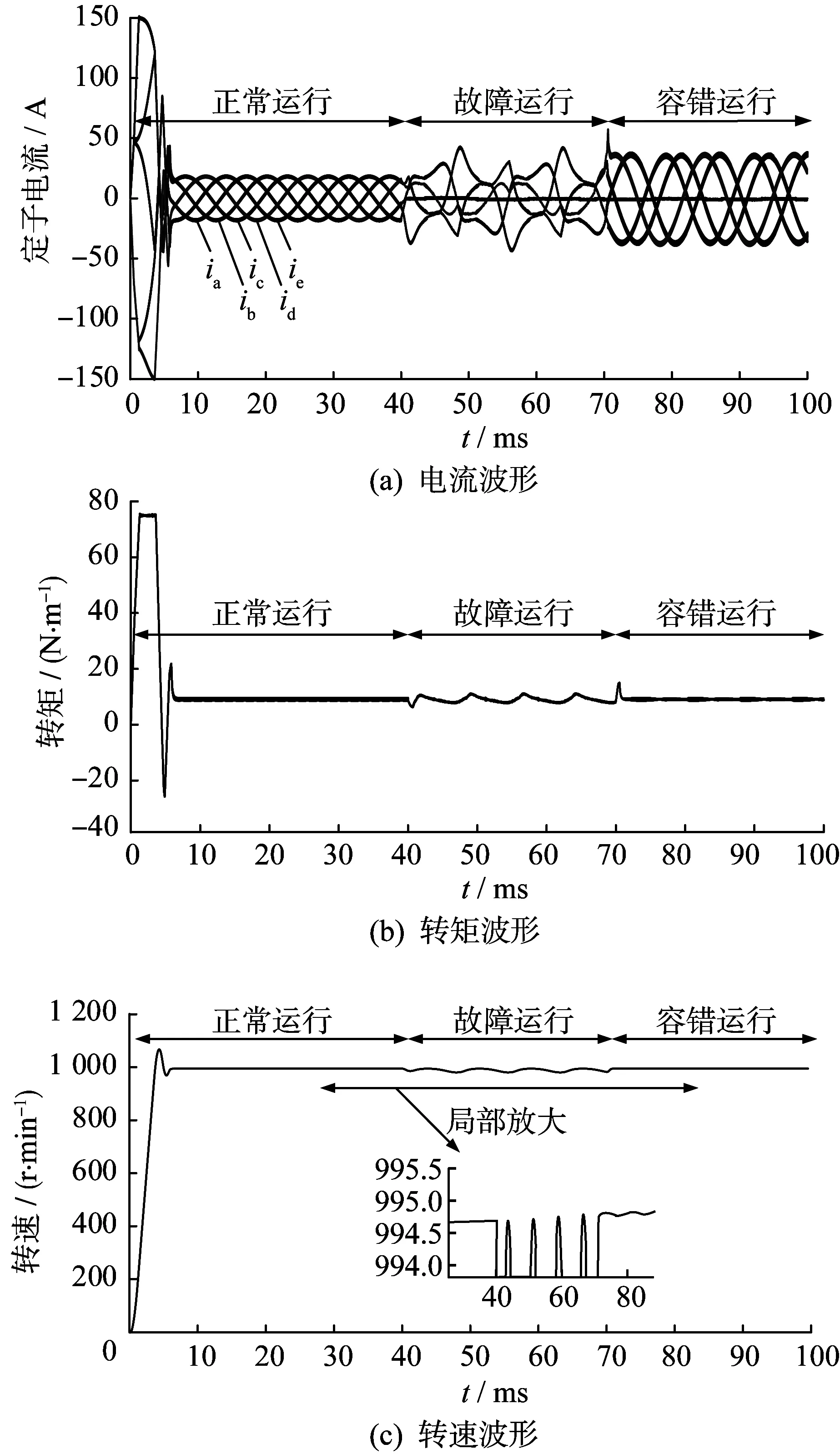
圖7 直接轉矩容錯控制電流、轉矩和轉速響應

由圖7可知，正常狀態運行下FP-PMSM定子電流波形正弦度良好，轉矩輸出平穩；出現缺相故障時，A相電流變為零，B、C、D、E相電流均發生嚴重的電流畸變，電動機轉矩及轉速出現較大的脈動；在容錯控制時，由于輸出轉矩與正常運行狀態相近，圖7（a）中定子電流幅值出現了相應地增長，且保持良好的正弦度。構建虛擬電壓矢量，將x-y子空間中y軸分量合成為零，對諧波分量起到了抑制。因此，在圖7（b）和圖7（c）中，電動機轉矩和轉速均從較大波動變為較小波動。

以平穩運行時轉矩均值9.1 N·m作為基準值，按轉矩最大、最小值的差值與基準值的比值的百分數作為脈動系數，計算得出正常運行時的脈動系數為9.3%，故障時為52.7%，經容錯控制后變為12.3%。仿真結果驗證了本文控制方法的有效性。

4 結 語

本文針對FP-PMSM缺一相故障，提出了一種基于虛擬矢量的DTC容錯控制方法，仿真結果驗證了該方法的可行性。對故障后的電壓矢量進行重構，得到虛擬電壓矢量，可有效抑制諧波分量的產生，減少最優電壓矢量的備選個數，降低系統控制復雜性。采用基于虛擬矢量的DTC開關表進行容錯控制，轉矩脈動較故障發生時大大降低，故障后電動機的工作水平恢復到與原來相近。但系統對最優矢量的選取，仍采用滯環控制，對系統性能有一定的影響。因條件所限沒有進行實機驗證，在以后的研究工作中將進一步完善。