煤礦救援機器人可折展水彈輪式結構分析與優化

尚祖恩 趙麗娟 劉雄豪 金 鑫

遼寧工程技術大學機械工程學院，阜新，123000

0 引言

為使礦井救災工作在災變井巷非結構化空間地形內順利開展，人們研發了可代替或部分代替救護人員并能及時、快速深入礦井災區進行環境信息探測與生命跡象搜尋工作的特種救援機器人[1-2]。目前礦用救援機器人主要包括小型環境探測機器人和營救機器人[3]，其中輪式救援機器人控制簡單，移動穩定、高效，一直有著廣泛應用，但其越障能力不足，在非結構化環境下適應能力較弱。因此學者們提出了輪履[4]、輪腿[5-6]等復合式和將類輪結構代替為輪部[7]的方法，通過改變不同的運動模式使救援機器人具有較高的環境適應能力。但由于煤礦井下環境極其惡劣，滿足防爆要求及穿越狹小空間的能力對救援機器人的自重與尺寸均有較嚴格限制[8]，因此煤礦救援機器人的結構創新性設計至關重要。

折紙是一種起源于中國的古老東方藝術表達形式[9]，設計折痕可將折紙從2D平面折疊成所需的3D立體結構，折紙與機器人相互結合形成了特有的前沿領域。天津大學陳焱團隊對折紙機器人進行了歸納總結[10]，將其分為骨架型折紙機器人、驅動型折紙機器人以及外殼型折紙機器人三種類型，其中骨架型折紙機器人將折紙作為變形結構，驅動型折紙機器人將折紙結構作為驅動器，外殼型折紙機器人將折紙結構作為保護外殼。折紙機器人可通過編程手段將制造與控制緊密結合，通過設計折痕使煤礦救援機器人具有較高的可定制性和適應性[11-12]，而且可以顯著減小機器人質量并降低材料成本，同時利用折紙結構的可展特性使救援機器人具有一定程度的可變形性。

水彈折紙結構具有的徑向可展特性被廣泛應用于機器人設計中，FANG等[13]設計了一種蚯蚓狀仿生機器人，通過水彈折紙結構的周期性軸徑向變形模擬蚯蚓的蠕動。LEE等[14]設計了一款名叫SNUMAX的折紙輪式機器人，其輪部由水彈結構與履齒組成，采用層壓加工工藝制成了模型。該輪式結構可折展、質量小、履齒結構在增大水彈輪式結構折展比的同時還可增加與地面的接觸摩擦力。但上述設計都未考慮防爆結構對水彈輪式結構力學特性的影響，無法直接應用于礦用救援。

有關折疊結構的分析研究較多[15]，其中水彈折紙結構相關的研究包括：考慮紙張厚度的厚板折紙建模理論[16]、構建水彈折紙結構初始無變形狀態的幾何分析方法[17]、對稱運動條件下水彈折紙結構的剛性可折疊運動學分析[18]、水彈折紙管狀結構的軸向扭轉運動學分析[19]、以多種四邊形為基本單元的水彈輪式結構運動學建模[20]、利用鉸鏈改變水彈折紙結構剛度的設計思路[21]、對基于水彈折紙圖案的折紙支架熱機械行為分析[22]、對水彈折紙管的折疊機理以及參數規律分析[23]、對由形狀記憶合金驅動的水彈輪系統動力學分析[24]和水彈折紙結構基本單元的雙穩態行為研究[25]等。本文以小型環境探測機器人作為研究對象，考慮水彈輪結構參數對礦用救援機器人承載能力和疲勞壽命的影響，結合實際應用對平行四邊形水彈輪式結構進行多目標優化。首先對以平行四邊形為基本單元的水彈輪式結構進行運動學分析，通過對比不同基本單元水彈輪式結構的承載能力確定基本單元構型，針對平行四邊形水彈輪式結構疲勞損傷問題結合連續介質損傷力學理論對其結構疲勞壽命進行分析預測及多目標優化，并通過多材料3D打印制造模型進行試驗驗證。

1 平行四邊形水彈輪式結構運動學建模

1.1 折痕設計

水彈輪式結構的折紙圖案由六折痕頂點基本單元組成，如圖1所示，水彈管狀結構兩端沿軸向收折，同時由中心位置沿徑向展開，這種折紙結構可用作可變徑輪式結構。

(a)初始狀態 (b)展開狀態圖1 水彈管狀結構徑向折展Fig.1 Radial expansion of waterbomb tubular structures

由正方形、矩形、平行四邊形為基本單元組成的水彈管狀結構折痕展開圖見圖2。其中實線為山折痕，虛線為谷折痕，m、n分別為橫縱向單元數，圖2中m=2，n=6。設定正方形基本單元邊長為2la，矩形邊長為2la、2lb，平行四邊形邊長為2la、2lb，傾斜角度為α。本文以平行四邊形為例，但其建模公式同樣適用于正方形和矩形。

(a)正方形基本單元及折痕圖

(b)矩形基本單元及折痕圖

(c)平行四邊形基本單元及折痕圖圖2 水彈結構折痕圖Fig.2 Crease diagram of waterb omb structures

圖3為平行四邊形水彈輪式結構及其折痕圖，此時m=3，n=9。圖3a為水彈折紙結構的輪身展開圖；圖3b為端蓋展開圖；通過組合得到圖3c所示的水彈輪式結構模型。定義ta為輪身展開圖上下兩側拼接三角形中線長度，tb為端蓋內正多邊形中心到各頂點的距離。

(a)輪身展開圖(b)端蓋展開圖

(c)水彈輪式結構模型圖3 平行四邊形水彈輪式結構Fig.3 Parallelogram waterb omb wheel structures

1.2 運動學建模

為保證水彈輪式結構變形性能，假設折疊部分為理想轉動關節，對其進行運動學分析。根據實際工作需要將其分為：輪軸端層(水彈輪式結構端蓋與傳動軸連接位置)、輪支撐層(輪軸端層與接觸層連接位置)、輪接觸層(與地面接觸位置)。定義水彈輪式結構軸線為Zc軸，其中Xc軸過輪接觸層頂點Tc3，建立基礎圓柱坐標系，如圖4所示。為探究水彈輪式結構的運動特性，假設同層水彈輪式結構基本單元運動行為相同，水彈輪式結構兩端運動行為一致。

圖4 基礎圓柱坐標系Fig.4 Basic cylindrical coordinate system

綜上所述，確定平行四邊形水彈輪式結構的初始配置參數為α、m、n、la、lb、ta、tb。

輪軸端層模型如圖5所示，基礎圓柱坐標系OcXcYcZc下折痕頂點Ec1、Ec2、Ec3如圖5a所示，構建空間直角坐標系O1X1Y1Z1如圖5b所示，其中O1為水彈輪式結構端蓋中心點，Z1軸與Zc軸重合，X1軸過點Ec1，Y1軸符合右手定則，Ec1Ec2在X1O1Z1平面內。

(a)圓柱坐標系下輪軸端層模型

(b)直角坐標系下輪軸端層模型圖5 平行四邊形水彈輪式結構軸端層模型Fig.5 Shaft end layer model of parallelogramwaterb omb wheel structures

輪軸端層狀態變量為θe1、θe2、le，其中,θe1為Ec1Ec2Ec3與Ec1Ec2E′c3兩平面的二面角，θe2為Ec1Ec2與X1軸延長線的夾角，le為端蓋中心距圓柱坐標系原點Oc的距離，輪軸端層運動學建模如下：

(1)

(2)

(3)

輪支撐層模型如圖6所示，圓柱坐標系OcXcYcZc下折痕頂點Sc1～Sc5如圖6a所示，構建空間直角坐標系O2X2Y2Z2以Sc3為原點，Sc3與O2重合，Z2軸垂直于平行四邊形上下兩條邊，Y2軸與上下兩條邊平行，X2軸符合右手定則垂直于基本單元，如圖6b所示。

(a)圓柱坐標系下輪軸端層模型

(b)空間直角坐標系下輪軸端層模型圖6 平行四邊形水彈輪式結構支撐層模型Fig.6 Support layer model of parallelogramwaterb omb wheel structures

支撐層狀態變量為θs1、θs2、θs3、θs4、ls、rs，其中，θs1、θs2分別為Sc2Sc3和Sc3Sc4在X2O2Z2平面的投影與Z2軸所夾的角度，θs3、θs4分別為Sc1Sc2Sc3與S′c1Sc2Sc3兩平面的二面角和Sc5Sc4Sc3與S′c5Sc4Sc3兩平面的二面角，ls為Sc3點距Oc點的距離，rs為過Sc3點作Zc軸垂線的距離。輪支撐層運動學建模如下：

(4)

(5)

(6)

(7)

(8)

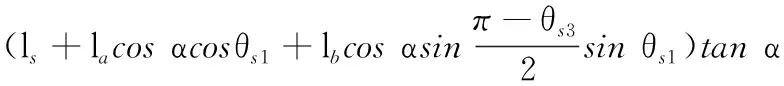
(9)

(10)

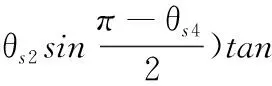
(11)

(12)

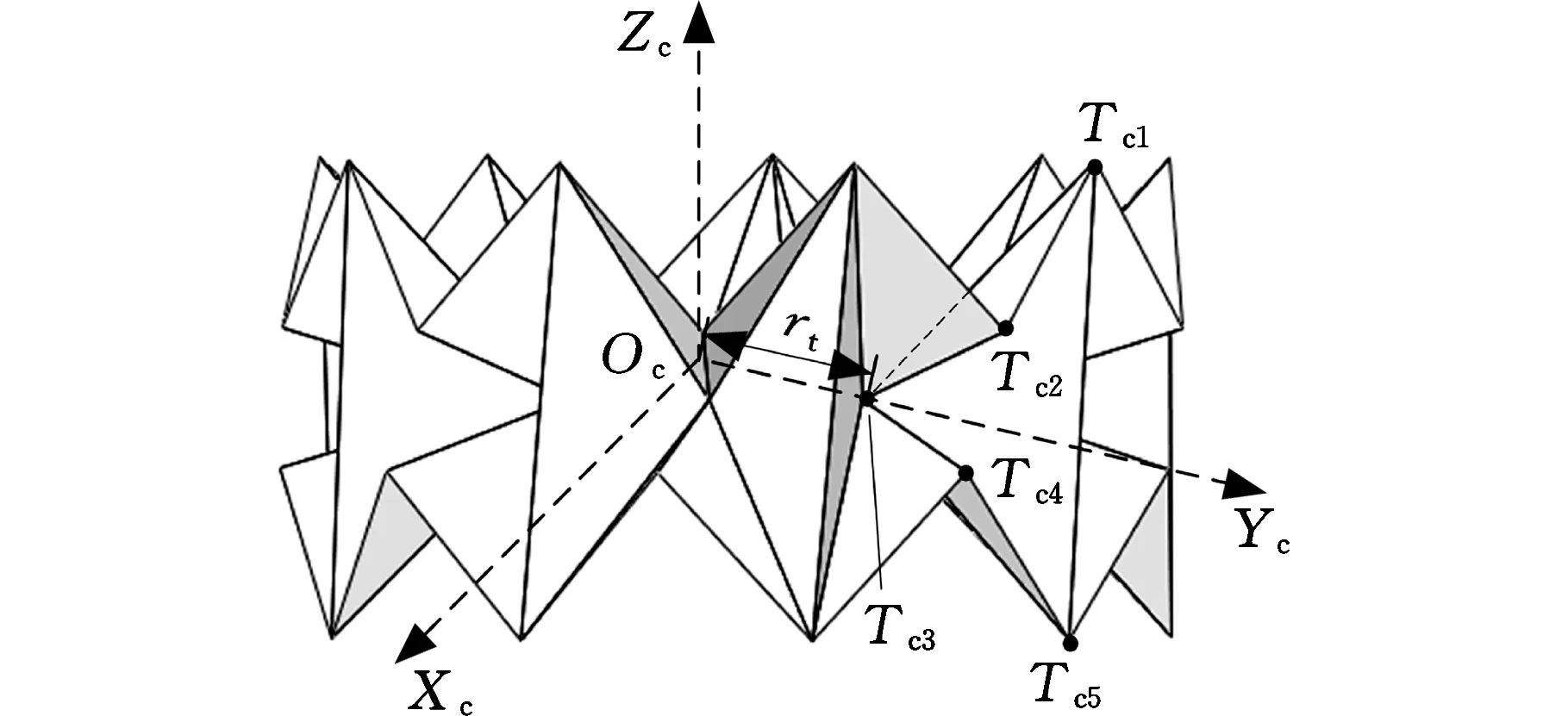
輪接觸層模型如圖7所示。圖7a中的Tc1～Tc5為圓柱坐標系下折痕頂點。構建空間直角坐標系O3X3Y3Z3，其中,Tc3為原點，與O3重合，Z3軸垂直于平行四邊形上下兩條邊，Y3軸與上下兩條邊平行，X3軸符合右手定則垂直于基本單元,如圖7b所示。

(a)圓柱坐標系下輪軸端層模型

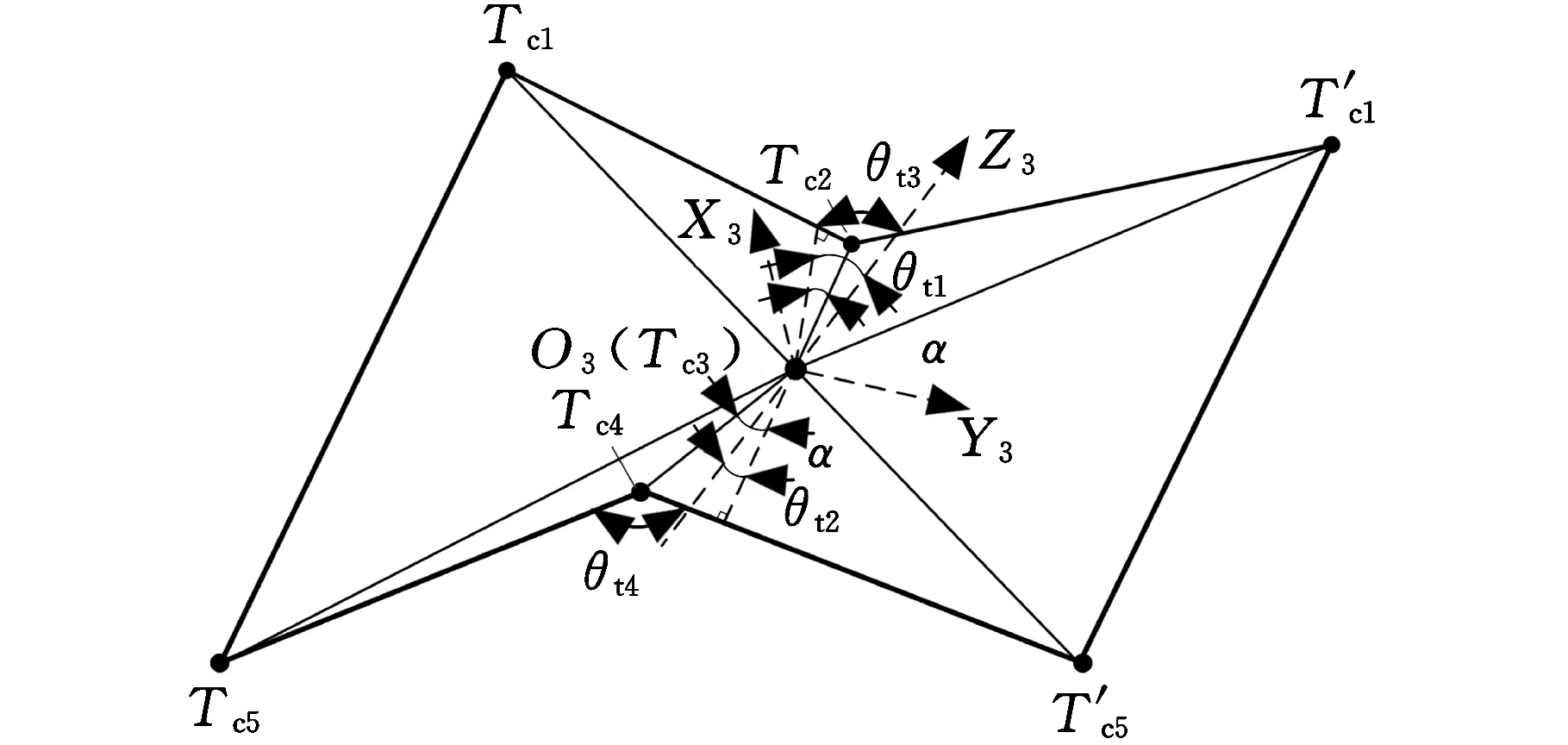
(b)直角坐標系下輪軸端層模型圖7 平行四邊形水彈輪式結構接觸層模型Fig.7 Contact layer model of parallelogramwaterb omb wheel structures

接觸層狀態變量有θt1、θt2、θt3、θt4、rt，其中,θt1、θt2分別為Tc2Tc3和Tc3Tc4在X3O3Z3平面的投影與Z3軸的夾角，θt3、θt4分別為Tc1Tc2Tc3與T′c1Tc2Tc3兩平面的二面角和Tc5Tc4Tc3與T′c5Tc4Tc3兩平面的二面角，rt為過Tc3點作Zc軸垂線的距離。由于水彈輪式結構原點Oc中心對稱，如圖7b所示，所以有以下角度關系：

θt1=θt2θt3=θt4

(13)

輪接觸層運動學建模如下：

(14)

(15)

(16)

通過對Tc2點進行運動學求解可得到水彈輪式結構徑向折展比φ：

(17)

其中,r′t、θ′t1與rt、θt1為展開完成與初始狀態參數。經迭代求解后設定初始參數α=0.256 rad、ta=26.7 mm、tb=61.5 mm、la=70 mm、lb=74.1 mm[17]。如圖8所示，當半徑rt在[67.9,103]mm范圍內變化時，輪軸端層二面角θe1在[1.06,1.56]rad范圍內變化，當rt=87.6 mm、θe1=1.56 rad時，θe1最大，隨后輪支撐層發生軸向扭轉運動[16]，θe1開始變小，最終當半徑rt=103 mm、θe1=1.41 rad時，水彈輪式結構完成展開運動。

圖8 折展過程中θe1變化趨勢Fig.8 Variation tendency of θe1 in the folding process

圖9所示為輪支撐層二面角θs3變化趨勢，當半徑rt在[67.9,103]mm范圍內變化時，輪軸端層二面角θs3在[0.7,1.07]rad范圍內變化，當rt=83.5 mm時，θs3=1.01 rad，此時θs3達到最大。隨后輪支撐層發生軸向扭轉運動，θs3開始變小，最終當半徑rt=103 mm、θs3=0.7 rad時，水彈輪式結構完成展開運動。

圖9 折展過程中θs3變化趨勢Fig.9 Variation tendency of θs3 in the folding process

經運動學分析發現，水彈輪式結構在運動狀態Ⅰ～Ⅱ階段為剛性折紙運動，Ⅱ～Ⅲ階段為結構形變，二面角θe1和二面角θs3在展開過程中存在先增大后減小的變化趨勢，平行四邊形水彈輪式結構支撐層在折展過程中存在軸向扭轉運動，位置發生在軸端層和支撐層連接位置，從而為后續水彈輪式結構力學特性分析提供了理論基礎。

2 水彈輪式結構機械特性分析

2.1 徑向承載特性分析

利用有限元軟件ABAQUS/Explicit中顯式動力學求解器模擬不同基本單元的水彈輪式結構徑向壓縮過程，求解高度非線性問題。在m和n確定的情況下,探究關鍵結構參數基礎單元邊長la和lb、傾斜角度α、結構厚度v、單元間隙u(圖10)對水彈輪式結構徑向承載特性的影響，水彈輪式結構初始變量如表1所示，其中三種模型軟硬材料質量大小相同，模型總質量均為1.08 kg。

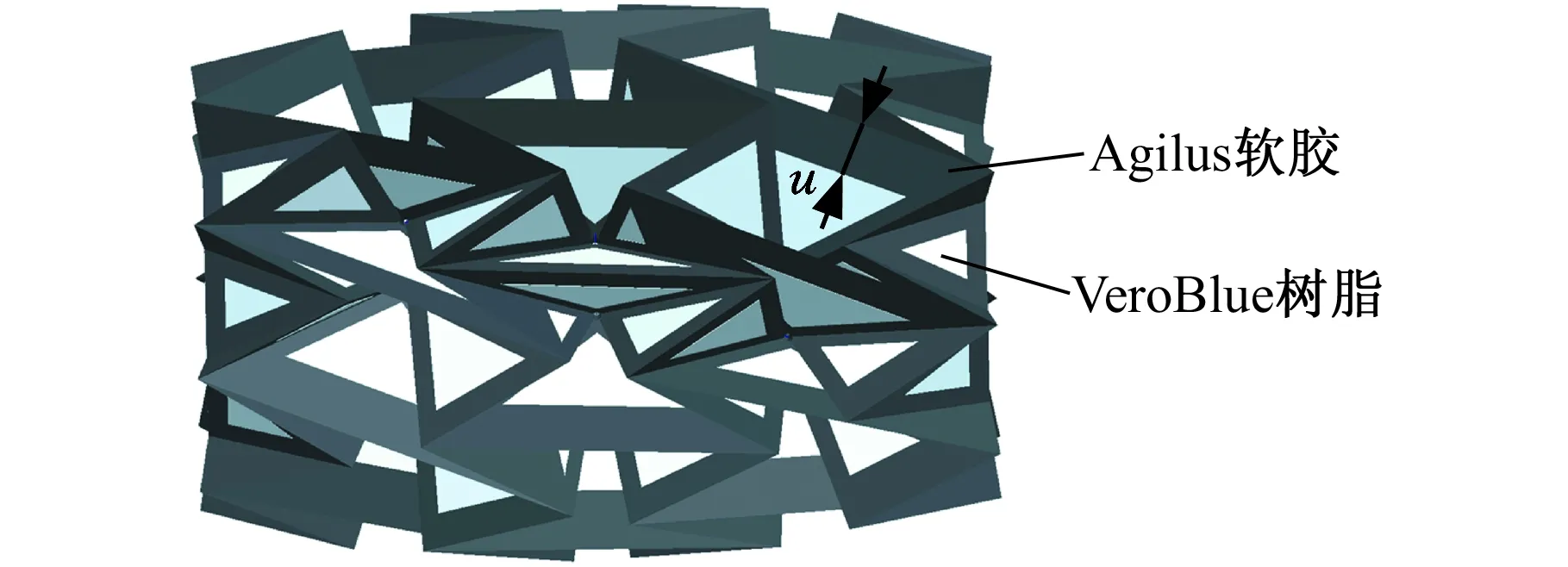
圖10 材料區域劃分Fig.10 Material area division

表1 初始關鍵設計變量

防爆和續航問題導致救援機器人質量較大，因此需對水彈輪式結構承載能力進行分析以保證其承載要求。設計的礦用救援機器人總質量約65 kg，由4個水彈輪式結構均布承載，單輪承受載荷為162.5 N。軟硬材料區域劃分如圖10所示，材料屬性如表2所示。水彈輪式結構軸線固定，固定一側端蓋，另一側施加位移載荷，然后對不同折展狀態下水彈輪式結構施加垂直向上的位移載荷U，達到材料強度極限后記錄極限承載力FLmax，結果如圖11～圖13所示。

表2 材料屬性

圖11 正方形水彈輪式結構極限承載力變化趨勢Fig.11 Variation tendency of square waterb omb wheelstructures’ ultimate bearing capacity

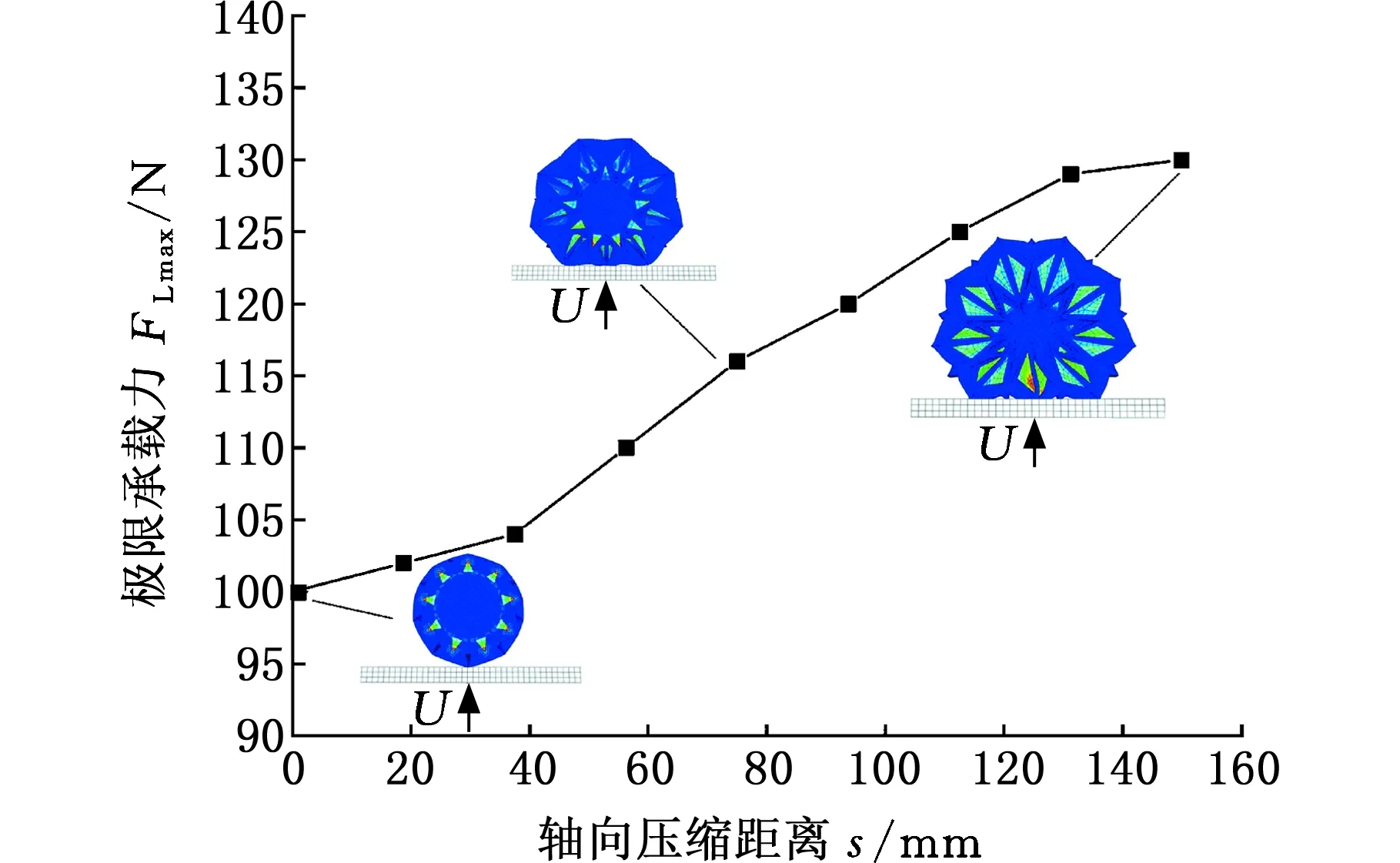
圖12 矩形水彈輪式結構極限承載力變化趨勢Fig.12 Variation tendency of rectangular waterb ombwheel structures’ ultimate bearing capacity

圖13 平行四邊形水彈輪式結構極限承載力變化趨勢Fig.13 Variation tendency of parallelogram waterb ombwheel structures’ ultimate bearing capacity

圖11～圖13給出了不同基本單元的水彈輪式結構折疊時極限承載力隨壓縮距離的變化曲線，可以看出隨著軸向壓縮距離s的增大，水彈輪式結構極限承載力逐漸增大，水彈輪式結構在軸向未壓縮狀態下，極限承載力最小，其中平行四邊形水彈輪式結構極限承載力大于正方形、矩形水彈輪式結構極限承載力，主要是由于平行四邊形水彈輪式結構軸向壓縮過程中發生了軸向扭轉變形。

由于初次設計三種水彈輪式結構對應的結構參數具有一定的探索性，使得水彈輪式結構的承載力并不理想，需要對水彈輪式結構進行優化設計。通過擬合多組數據構建平行四邊形水彈輪式結構軸向未壓縮狀態下極限承載力與其初始參數的函數關系如下：

(18)

其中,復相關系數R2=0.99，說明擬合函數具有較高的精度。

2.2 軸向壓縮疲勞壽命分析

為探究平行四邊形水彈輪式結構可靠性問題，基于連續介質損傷力學理論對水彈輪式結構軸向壓縮載荷下進行裂紋萌生疲勞壽命預測，將等效應變范圍作為損傷參量,得到疲勞載荷下水彈輪式結構裂紋萌生疲勞壽命預測模型如下：

(19)

(20)

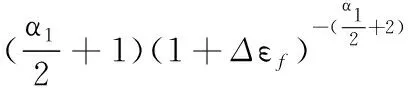
(21)

其中,經疲勞試驗數據擬合計算確定Agilus軟膠材料常數a、b、μ1、α1分別為1.12、1926、1.033、1.722，Δεf為等效應變范圍。

采用ABAQUS仿真模擬平行四邊形水彈輪式結構的準靜態徑向展開過程，沿水彈輪式結構軸線向內施加150～200 N疲勞載荷，通過應力應變分析確定易發生疲勞破壞區域，結果如圖14、圖15所示。

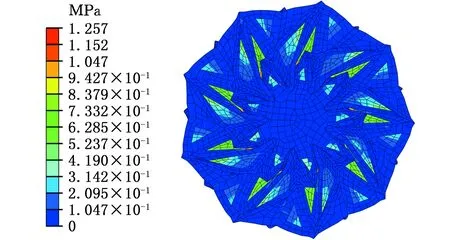
(a)應力云圖

(b)應變云圖圖14 軸向150 N載荷下應力應變云圖Fig.14 Stress-strain contours under an axial loadof 150 N

(a)應力云圖

(b)應變云圖圖15 軸向200 N載荷下應力應變云圖Fig.15 Stress-strain contours under an axial loadof 200 N

由圖14、圖15可見，在疲勞載荷作用下水彈輪式結構危險位置為端蓋邊緣環狀區域，提取危險位置的主應力計算得到等效應變范圍Δεf=0.5861，經式(19)計算疲勞壽命預測值Nf=1474，可見軸向加載產生的疲勞裂紋會對水彈輪式結構壽命有較大影響，因此為提高水彈輪式結構使用壽命，調整設計參數擬合得到裂紋萌生疲勞壽命函數關系如下：

(22)

復相關系數R2=0.99，模型擬合效果較好。

3 平行四邊形水彈輪式結構多目標優化

以基礎單元邊長、傾斜角度、水彈輪式結構結構厚度、單元間隙為設計變量x，以水彈輪式結構的折展比為約束條件、以極限承載力和疲勞壽命最大為目標，建立優化模型如下：

(23)

其約束區間如下：

(24)

其中，Sn為設計變量庫。各單目標具有同等重要程度，因此極限承載力權重λ1=0.5，裂紋萌生疲勞壽命權重λ2=0.5。應用遺傳算法求解優化問題，設定種群大小為100，精英數目為10，交叉后代比例為0.75，最大進化代數為200，停止迭代數為200，適應度函數值偏差默認為1×10-6，求解確定優化前后關鍵設計變量如表3所示，性能指標對比如表4所示。

表3 水彈輪式結構關鍵設計變量

表4 優化前后性能指標對比

由表4可見，優化后折展比提高約15.8%，極限承載力和裂紋萌生疲勞壽命提高約40.7%和55.4%，水彈輪式結構整體性能提升較明顯。

4 試驗驗證

通過多材料3D打印制作比例為1∶2的平行四邊形水彈輪式結構實物模型進行折展可行性試驗，試驗測試過程如圖16、圖17所示。將實物模型壓縮，測量得折展比約為2.02，與理論值之間誤差為4.72%，試驗結果驗證了運動學模型的準確性與優化過程的有效性。

圖16 輪徑未折展狀態測量Fig.16 Measurement of wheel diameter in theunfolded state

圖17 輪徑展開狀態測量Fig.17 Measurement of wheel diameter in thefolded state

圖18 水彈輪式結構徑向壓縮試驗Fig.18 Radial compression test of waterbombwheel structures

為驗證優化后水彈輪式結構符合承載力要求，對1∶1實物模型進行試驗測量，如圖18所示。將水彈輪式結構通過固定模具固定到傳感器上，通過徑向壓縮水彈輪式結構測出對應承載力，徑向壓縮測試使用WDW-2D型微機控制電子萬能試驗機，壓縮速度為0.5 mm/min，利用固定模具調整水彈輪式結構折展狀態，測試5次后取平均值得到極限承載力，如圖19所示。

圖19 仿真與試驗結果對比Fig.19 Comparison of simulation and test results

由圖19可知，優化后水彈輪式結構極限承載力理論值為170.3 N，實測極限承載力為159.1 N，兩者誤差為6.58%，優化后結構更加趨于合理。

平行四邊形水彈輪式結構軸向疲勞試驗如圖20所示，對試件施加150～200 N的垂向交變載荷，經1718次疲勞試驗結構出現疲勞裂紋，其中危險點部位最先出現微小裂紋，如圖21所示。可以看出，產生裂紋位置與仿真危險位置一致，出現在端蓋邊緣位置。優化后裂紋萌生壽命理論值為2291次，實測值與理論值之間誤差為25.01%，在工程可接受范圍之內，驗證了疲勞壽命預測的有效性。

圖20 水彈輪式結構軸向壓縮試驗Fig.20 Axial compression test of waterbombwheel structures

圖21 疲勞破壞區域Fig.21 Fatigue failure area

5 結論

(1)本文提出了一種平行四邊形水彈輪式結構運動學建模方法，并對平行四邊形水彈輪式結構進行了運動學分析，發現二面角θe1和θs3具有先增大后減小的變化趨勢，平行四邊形水彈輪式結構端蓋層與支撐層連接位置存在軸向扭轉運動。

(2)為探究扭轉運動是否對水彈輪式結構的承載特性產生影響，利用有限元軟件對水彈輪式結構極限承載力進行分析，在模型的質量相同條件下對比三種不同基本單元水彈輪式結構計算結果發現，平行四邊形水彈輪式結構承載特性較好，增加了水彈輪式結構的設計靈活性，提高了水彈輪式結構承載能力。

(3)基于連續介質損傷力學理論對平行四邊形水彈輪式結構軸向壓縮載荷下疲勞壽命進行預測，發現端蓋邊緣為易發生疲勞破壞區域。

(4)以折展比為約束條件，以極限承載力、疲勞壽命作為目標函數進行多目標優化，優化后平行四邊形水彈輪式結構折展比、極限承載力、疲勞壽命分別提高約15.8%、40.7%、55.4%，經多材料3D打印制作平行四邊形水彈輪式結構進行試驗測試，試驗結果驗證了擬合模型的有效性和可行性，為煤礦救援機器人可折展輪式結構的工程應用提供了有效設計方案。