無人機繞速度矢量軸滾轉機動自適應滑模邊界保護控制

劉曉棟，吳慶憲，陳 謀，邵書義

（南京航空航天大學自動化學院,南京 211106）

無人機相比有人機，具有以下優點：尺寸更小，隱身性更好，不受駕駛員生理條件限制，具有更大的性能包線［1-3］。隨著現代空戰理念的發展，無人機作戰必須具備大機動能力。大機動能力指無人機在超過失速迎角之后，仍有對姿態做出調整的能力［4］。大機動無人機應用在現代戰場可以實現機頭快速指向與小半徑轉彎使之迅速處于有利位置，所以研究大機動無人機控制技術具有重要的理論意義和應用價值。由于無人機沒有經驗豐富的駕駛員，如何保證無人機的飛行安全是需要首先解決的問題。

為了保證無人機的飛行安全，可在解算無人機安全邊界的基礎上進行邊界保護控制。安全邊界的定義與解算近年來有了新的發展，可以歸納為可達平衡集和可達集兩種方法。許多學者已將上述方法應用于各類飛行器的邊界解算中。雍可南綜合運用可達平衡集與可達集解算出F16飛機的邊界［5］。季雨璇等應用可達平衡集實現戰斗機俯仰機動和滾轉機動可達區域的求解，為實際飛行提供了參考［6］。針對狀態約束機動，上述文獻將可達平衡集和可達集應用于各類飛行器的邊界解算，可以準確解算邊界，然而其解算過程耗時冗長，不能滿足大機動無人機邊界保護的實時性要求，所以需要對上述方法進行改進以提高解算實時性。當解算出無人機的安全邊界后，可以應用邊界保護系統，使飛行狀態不越界，進而保證飛行安全。邊界保護系統的核心是保證飛行器的安全同時最大化機動能力。但傳統施加限幅器的方法很大程度上限制了飛行器的機動性，所以需要發展新型結構的邊界保護系統［7］。于媛媛采用指令約束的新型邊界保護系統實現對期望指令的約束，保證了機動安全［8］。當應用上述新型邊界保護系統實現對無人機機動指令的約束后，還需進行無人機姿態跟蹤控制器的設計。

無人機大機動屬于短周期姿態運動，然而機動過程中迎角遠超失速迎角，會產生強耦合和強非線性［9］，使傳統線性控制方法不能滿足控制精度和性能的要求，需要采用非線性方法設計控制器。近些年，動態逆［10］和滑模［11-15］等非線性控制方法廣泛應用于飛行控制和工業等領域。滑模控制方法由于其良好的魯棒性，已成功運用于大機動飛行控制中［11］，并通過采用飽和函數或雙曲正切函數替代符號函數的方法，有效抑制了滑模控制器的抖振［12］。顧攀飛等為研究高超聲速飛機再入飛行時面臨的不確定故障問題，設計了一種自適應滑模容錯控制器［13］。Cao等提出自適應容錯控制方案，用于研究外部干擾和執行器失效作用下的航天器姿態跟蹤問題［14］。然而無人機大機動飛行過程中，如何抑制模型不確定性和外部干擾帶來的不利影響是控制器設計必須考慮的。

為抑制模型不確定性和外部干擾的不利影響，徑向基神經網絡（Radial basis function neural network，RBFNN）和非線性干擾觀測器（Nonlinear disturbance observer，NDO）方法在控制器的設計中得到了廣泛的應用。Chen等利用RBFNN逼近系統不確定性，實現了三自由度直升機的容錯控制［15］。Zhang等 設 計了基于NDO的反步 控 制器，消除了時變擾動對系統的不良影響［16］。根據上述研究成果可知，通過綜合運用RBFNN和NDO方法可以抑制系統不確定性和外部干擾的不利影響，從而提高控制器的控制精度。

受上述分析啟發，本文主要研究大機動無人機繞速度矢量軸滾轉機動的邊界保護控制。主要內容包括：第1節建立無人機姿態模型，并給出整個保護控制系統的結構框圖。第2節基于二分法思想改進可達平衡集并引入指令約束方法，實現在線安全邊界解算與期望指令生成功能。第3節引入RBFNN逼近系統不確定項，并利用二階非線性干擾觀測器補償系統復合干擾，進一步設計自適應滑模邊界保護控制器。第4節給出改進可達平衡集邊界解算與繞速度矢量軸滾轉機動的仿真結果。

1 問題描述

無人機繞速度矢量軸滾轉機動屬于短周期姿態運動，對于機動過程中的長周期軌跡運動狀態量則任其自然演變，因此本文控制器設計只考慮短周期的姿態運動狀態量。無人機姿態運動方程可寫為［9］

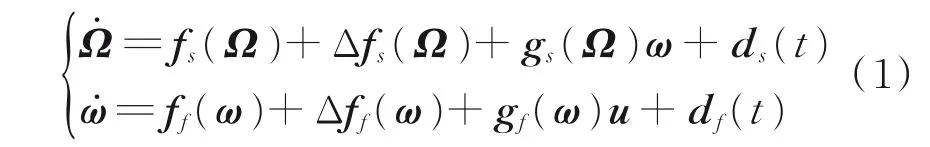
式中：Ω=[α，β，μ]T為姿態角狀態向量，α、β、μ分別為迎角、側滑角和繞速度矢量軸滾轉角；ω=[p，q，r]T為姿態角速率狀態向量，p、q、r分別為滾轉、俯仰和偏航角速度；u=[δa，δc，δr，δy，δz]T為系統控制向量，δa、δc、δr、δy和δz分別為副翼偏轉角、鴨翼偏轉角、方向舵偏轉角、側向推力矢量偏轉角和縱向推力矢量偏轉角；fs(Ω)=[fα，fβ，fμ]T和ff(ω)=[fp，fq，fr]T為系統狀態函數向量；gs(Ω)和gf(ω)為系統控制系數矩陣；Δfs(Ω)和Δff(ω)為系統不確定項；ds(t)和df(t)為外部未知有界干擾向量。

根據式（1），本文定義繞速度矢量軸滾轉角速率為ps，且可表示為

當無人機進行繞速度矢量軸滾轉機動時［17］，ps易發生越界，超出安全可控范圍導致失控。如何在保證安全的前提下進行機動，又避免盲目限制ps導致機動性能的損失，是本文研究的核心。本文圍繞此問題，從邊界保護與姿態控制兩方面展開研究，整體結構框圖如圖1所示。

圖1 無人機邊界保護系統框圖Fig.1 Block diagram of UAV boundary protection system

為了便于對系統穩定性的分析，需要引入如下假設和引理。

引理1［20］對于初始條件有界的系統，如果存在一個連續且正定的Lyapunov函數V(x)∈C1，且滿 足γ0(‖x‖)≤V(x)≤γ1(‖x‖)，若 有?(x)≤-κV(x)+c，這里γ0，γ1：Rn→R為K∞類函數且κ，c為正常數，則系統的解x(t)一致有界。

引 理2［12］對 于 任 意 的b＞0和z∈Rm，有 如下不等式成立：0＜‖z‖-zTtanh(z/b)≤m?b，其中?滿足?=e-(?+1)，即有?=0.2785 。

引理3［15］對于集合Z∈ΩZ?Rm，RBFNN可以逼近任意連續函數f(Z)：Rm→R，即可以描述為

如果n充分大，則可得

式中：W*為最優權值；ε*為最小逼近誤差，εˉ＞0為逼近誤差的上界。

2 邊界解算與約束指令生成

為了實現對無人機繞速度矢量軸滾轉機動的邊界保護，首先進行無人機在線邊界解算與期望約束 指 令 生 成 研 究。本 文 在 可 達 平 衡 集［5，7-8，21］中 引入二分法思想，利用遞歸方法實現邊界的快速解算，并引入指令約束方法實現對ps指令的約束。當解算ps的邊界時，將除μ以外描述無人機姿態運動的非線性方程簡寫為

式中：飛行狀態向量x=[α，β，p，q，r]T屬于有界域X；制向量δ=[δa，δc，δr，δy，δz]T屬于有界域U并且此區域由舵面偏轉限制；f(x，δ)為光滑的非線性函數。

為描述繞速度矢量軸滾轉機動的類型特征，引入參變量yμ為如下形式

將式（5，6）增廣為求解可達平衡集的系統方程，利用牛頓迭代法求解并將可達平衡集表示為

式中：xε表示穩定狀態向量；δε表示穩定控制向量。在進行穩態繞速度矢量軸滾轉時，側滑角β=0°，則將α和ps作為繞速度矢量軸滾轉機動的輸入［7］，利用牛頓迭代法對此時飛行狀態進行求解。通過設定α和ps的變化范圍與變化步長，可求解繞速度矢量軸滾轉機動的可達平衡集，并將其輪廓作為此類飛行狀態的安全邊界。

為方便研究，本文假定繞速度矢量軸滾轉機動的可達平衡集內部狀態連續，進而引入二分法對邊界解算的過程進行改進以提高計算速度。但實際在線邊界解算時，每一周期飛行狀態都在變化，此時無需要求α在確定范圍內按設定步長變化以進行ps全部邊界的解算，只需解算對應此時α狀態的ps邊界。當解算出ps邊界后，引入指令約束方法［8，21］將ps的期望指令psc約束在邊界范圍內，從而得到受約束的安全期望指令。為闡明ps在線邊界解算與約束指令生成的思想，給出流程圖（圖2）。

由圖2可知，基于改進可達平衡集方法的在線解算ps邊界與約束指令生成步驟如下：

圖2 繞速度矢量軸滾轉角速率在線邊界解算與約束指令生成流程圖Fig.2 Flow chart of online boundary solution and limited command generation for roll angle rate around velocity vector axis

（1）從系統中獲得psc及α等狀態量；

（2）設 定psmin=0°/s，ps=psmax=180或-180°/s，并將解算步長sps=1°/s作為遞歸的終止條件；

（3）設定牛頓迭代法的最大迭代步數和容許誤差；

（4）解算(α，ps)點狀態，得到所有舵面偏轉角度，若舵面偏轉均在偏轉限制范圍內，轉到第（7）步，否則轉到第（5）步；

（5）取psmid=(psmin+psmax)/2，解算(α，psmid)點狀態，得到所有舵面偏轉角度，若舵面偏轉均在限制范圍內，取psmin=psmid，否則取psmax=psmid；

（6）重復進行第（5）步，當滿足條件|psmaxpsmin|≤sps時，輸出psmax；

（7）當初始值psmax=180°/s或-180°/s，可分別解算ps的上界psu和下界psl；

（8）比較psc與psu數值大小，取值小的作為新psc；

（9）比較psc與psl數值大小，取值大的作為新psc；

（10）獲得滿足邊界約束的期望指令psc。

3 姿態控制器設計

根據引理3，當采用RBFNN逼近姿態系統不確定項Δfs(Ω)和Δff(ω)，其逼近結果可表示為

將式（8）代入式（1）可得

為提高控制器的性能和抗干擾能力，在姿態角回路和姿態角速率回路中引入二階非線性干擾觀測器［18］，并利用干擾觀測器輸出進行控制器的設計。

3.1 姿態角回路控制器設計

在姿態角回路中引入二階非線性干擾觀測器，其表達式可描述為

針對矩陣As，若給定矩陣Ps=PTs＞0，則存在一個正定矩陣Rs=＞0，使式（15）成立。

對Vos求導得

根據式（15），有如下不等式成立

此外根據式（10），有如下不等式成立。

式中：‖Φs(Z)‖≤τs，κs＞0為設計參數。

將式（18，19，20）代入式（17），可得

在上述設計的二階非線性干擾觀測器基礎上，設計姿態角跟蹤控制器。定義姿態角Ω跟蹤誤差Ωe=Ω-Ωc，則有

滑 模 面Ss設 計 為［22］：Ss=Cs Ωe=[Ss1，Ss2，Ss3]T，其中

選 擇cij(1≤i≤3，1≤j≤3)，使ci3s2+ci2s+ci1=0為Hurwitz穩定且(Cs gs(Ω))-1存在。

為減小姿態角系統抖振，此處采用雙曲正切函數tanh(·)代替滑模控制的符號函數［12］，從而設計姿態角回路虛擬控制律ωc為

式中：ks＞0，φs＞0和b＞0為設計參數；Tanh(Ss/b)=[tanh(Ss1/b)，tanh(Ss2/b)，tanh(Ss3/b)]T。

為實現對ps的保護控制，將姿態角回路控制輸出作為姿態角速率回路的輸入。無人機在大迎角下進行穩態繞速度矢量軸滾轉機動時，由于側滑角β=0°，此時穩定性坐標系的xs軸方向與速度矢量方向重合［7］，則繞機體軸角速率到繞速度矢量軸角速率存在如下轉換關系

式 中：[pc，qc，rc]T為 繞 機 體 軸 期 望 角 速 率 指 令，[psc，qsc，rsc]T為繞速度矢量軸期望角速率指令。則由式（25）可得psc=pccosα+rcsinα。將psc指令輸入在線邊界解算與指令約束模塊中，實現對psc的約束保護，然后進行式（25）的逆轉換，得到受約束的姿態角虛擬控制律ωcy=[pcy，qcy，rcy]T，再進行姿態角速率控制器的設計，進而實現無人機繞速度矢量軸滾轉機動的邊界保護控制。

為避免直接對受約束虛擬控制律ωcy求導，利用動態面控制方法解算其導數的近似值。設計時間常數為Γ=diag{τ11，τ12，τ13}的濾波器如下

定義濾波誤差ε=cy-ωcy，可得

式中：M(·)為緊集Π0與緊集Π1：(，Ss)上光滑函數向量，則M(·)在集合Π0×Π1存在上界Mˉ。同時由式（27）可得

為證明姿態角回路控制律的有效性，選取Lyapunov函數為

為了估計最優權值，設計神經網絡權值估計的自適應律為如下形式

式中：Λs=＞0，σs＞0為設計參數。

3.2 姿態角速率回路控制器設計

與姿態角跟蹤控制器設計類似，設計姿態角速率回路二階非線性干擾觀測器為

同上，針對矩陣Af，若給定矩陣Pf=P＞0，則存在一個正定矩陣Rf=＞0，使式（36）成立。

在上述設計的二階非線性干擾觀測器基礎上，設計姿態角速率跟蹤控制器。定義受約束安全姿態角速率ω的跟蹤誤差ωe=ω-ωcy，則有

滑模面Sf設計為：Sf=Cfωe=[Sf1，Sf2，Sf3]T，其中Cf設計要求同Cs。

由于姿態角速率在機動過程中變化速率快，所以在指數趨近律中引入冪次項‖Sf‖a以提高收斂速度，同時采用帶邊界層的飽和函數Sat(·)代替符號函數，以獲得更好的抗抖振性能［23］，從而設計受約束姿態角速率回路滑模控制律u為

式 中：kf＞0、φf＞0和0＜a＜1為 設 計 參 數，Sat(Sf)=[Sat(Sf1)，Sat(Sf2)，Sat(Sf3)]T，且帶邊界層的飽和函數Sat(·)的定義如下所示

式中：Δ＞0為邊界層厚度；sgn(·)為符號函數，定義如下

為證明姿態角速率回路控制律的有效性，選取Lyapunov函數為

對Vcf求導，并將式（40）代入式（43）得

（2）當 所 有|Sfi|≤Δ時，Sat(Sfi)=Sfi/Δ，i=1，2，3，則有

此時，結合式（41～43），有

綜合以上3種情況，有

為了估計最優權值，設計神經網絡權值估計的自適應律為如下形式

式中：Λf=＞0，σf＞0為設計參數。

3.3 穩定性證明

上述基于RBFNN和二階干擾觀測器的自適應滑模姿態控制器可以歸納為如下定理1。

定理1針對無人機繞速度矢量軸滾轉機動邊界保護控制系統，在式（10）成立的條件下，如果二階干擾觀測器的形式設計為式（11，32），神經網絡權值估計自適應律設計為式（31，48），則在所設計的姿態角控制律式（24）和受約束安全姿態角速率控制律式（40）的作用下，無人機姿態系統式（9）的跟蹤誤差是有界收斂的，并且閉環系統的所有信號是一致有界的。

為證明定理1，選取閉環系統Lyapunov函數為

對V求導，并將式（31，48）代入式（49）得

將式（51）代入式（50）可得

式中

根據式（52），由引理1可知，閉環系統所有信號是一致有界的，即上述定理1成立。

4 仿真結果

4.1 邊界解算仿真對比

為了說明改進可達平衡集方法進行邊界解算的快速性與準確性，本文給出ps的一類非在線邊界解算結果，并對比傳統可達平衡集。首先給定迎角的變化范圍為α∈[0°，90°]，繞速度矢量軸滾轉角速度的變化范圍為ps∈[-180°/s，180°/s]，同時給定初始條件為H=3000m，V=100m/s，β=0°，μ=0°。

本文通過構建α與ps的二維坐標圖表示所解算的安全邊界，兩種方法的邊界解算結果如圖3、4所示。圖3中的藍色區域為對應無人機狀態的安全飛行區域，藍色區域的外圍輪廓為安全邊界；圖4藍色右輪廓為安全上邊界，紅色左輪廓為安全下邊界，兩者之間的區域為安全飛行區域。對比解算結果圖3、4可知，改進可達平衡集可以準確求得可達平衡集的輪廓，即安全邊界。同時由兩種方法的耗時對比表1可知，改進可達平衡集解算點數更少，且解算時間更少。

圖3 傳統可達平衡集解算結果Fig.3 Reslult of traditional attainable equilibrium set

圖4 改進可達平衡集解算結果Fig.4 Reslult of improved attainable equilibrium set

表1 耗時對比Table1 Time consumption comparison

4.2 邊界保護控制系統仿真驗證

給定繞速度矢量軸滾轉機動仿真初始條件為：高度H0=3000m，速度V0=100m/s；初始姿態角為α0=60°，β0=0°，μ0=0°；初 始 姿 態 角 速 率 為p0=q0=r0=0°/s；參考輸入信號為迎角αc=60°，側滑角βc=0°，繞速度矢量軸滾轉角μc［5］。

仿真時，在無人機姿態模型中加入參數不確定性和外部數值干擾，其中氣動系數不確定性為±20%，姿態角回路和姿態角速率回路干擾為

姿態角回路干擾觀測器設計參數為：ps1(Ω)=ps2(Ω)=3[α，β，μ]T和Ls1(Ω)=Ls2(Ω)=3I3。

姿態角速率回路干擾觀測器設計參數為：pf1(ω)=pf2(ω)=3[p，q，r]T和Lf1(ω)=Lf2(ω)=3I3。

控制器參數的選擇為：b=0.4 ；Δ=0.05 ；Cs=Cf=[4，3，2；1，4，2；2，3，4]；a=0.9 ；φs=φf=0.5 ；ks=diag{4，4，4}；kf=diag{8，8，8}；κs=κf=10；Λs=Λf=diag{5，5，5}；σs=σf=0.5 ；濾 波 器時間常數為Γ=diag{0.08 ，0.08 ，0.08 }。則仿真結果如圖5～7所示。

圖5 姿態角跟蹤曲線Fig.5 Attitude angle tracking curves

圖6 姿態角速率跟蹤曲線Fig.6 Attitude angle rate tracking curves

由仿真曲線圖5、6可知，所設計的自適應滑模姿態控制器可以使無人機有效跟蹤期望姿態角指令[αc，βc，μc]T及 受 約 束 后 的 姿 態 角 速 率 指 令[pcy，qcy，rcy]T。由仿真曲線圖7可知，當繞速度矢量軸滾轉角速度的期望指令psc超出在線解算的上邊界psu或下邊界psl時，指令約束器就會將其約束在邊界范圍內，既保證了機動的安全性，又不損失機動性能。繞速度矢量軸滾角速度ps在整個機動過程中沒有越界，因此所設計的邊界保護控制方法是有效的。

圖7 繞速度矢量軸姿態角速率曲線Fig.7 Attitude angle rate tracking curves around velocity vector axis

5 結 論

本文針對無人機繞速度矢量軸滾轉機動邊界保護控制系統，首先研究了基于二分法思想的改進可達平衡集確定安全邊界算法，加快了在線解算邊界的速度，同時引入指令約束方法實現了對期望指令的約束。其次，設計了基于RBFNN和二階非線性干擾觀測器的滑模控制器，實現了外部擾動和系統不確定性綜合作用下的大機動無人機姿態系統的指令跟蹤控制。通過選取閉環系統Lyapunov函數，證明了所設計控制系統的穩定性。最后，通過數字仿真驗證了所設計邊界保護控制方法的有效性。