多旋翼無人機二維超聲波測風算法研究*

周川川 李傲梅

（陸軍炮兵防空兵學院信息工程系 合肥 230031）

1 引言

如何提高超聲波測風傳感器測量精度一直是超聲波測風領域的研究熱點，但其應用領域多是對固定點位風場二維水平風信息的長期測量。對于采用二維正交測風陣列結構布局的二維超聲波測風設備，其工作前，需將設備按要求進行“調平”和“對北”，“調平”是指將二維測風陣列調成水平狀態，“對北”是指借助指北針等輔助器材讓設備對正北向。“調平”和“對北”是二維超聲波測風傳感器發揮靈敏優勢、實現對水平風速及風向準確測量的基礎，而旋翼無人機由于受氣流擾動、機架震顫、機體搖擺等因素影響，懸停狀態下不能時刻保持平衡狀態，如若將二維超聲波測風傳感器安裝于無人機平臺，勢必影響超聲波測風傳感器的測量準確性。

為將二維超聲波測風傳感器與多旋翼無人機的優勢結合，以實現對空中原位水平風場信息的準確測量，本文從超聲波測風原理著手，通過對三維超聲波測風傳感器系統測風原理分析，基于旋轉矩陣原理，提出一種機身傾斜情況下，二維超聲波測風傳感器也能完成對水平風測量的方法，為多旋翼無人機二維超聲波測風方案的實現提供算式依據。

2 超聲波測風基本原理

超聲波是頻率高于20000Hz的聲波，具有指向性好，穿透能力強，能量較集中等特點，相較于氣體，其在固體及液體中傳播距離較遠，在測距測速、工業探傷、醫用、清洗、殺菌消毒等領域均有較為成熟的運用。

2.1 超聲波特性

1）衰減特性

能量衰減是超聲波傳播時的固有特性，衰減程度同自身頻率及傳輸介質均相關，在理想的空氣中，擴散現象是超聲波能量衰減主要因素，超聲波的能量和傳輸距離成反比的關系［1～2］。控制衰減程度有助于提高其應用領域測量范圍，實驗表明在空氣中超過1m的傳輸距離時，其能量衰減較快，200kHz超聲波在0.1m～0.5m能維持在10%左右的衰減幅度［3］。

2）傳播特性

超聲波傳播速度主要受溫度、濕度、壓強等影響，如在一些應用領域，常用溫度補償方式提高超聲波測量的準確性，所以在使用超聲波進行測量時應該盡量用超聲波在空氣的實際速度作為參數，如超聲波在風速測量的的波速表示為

其中r是比熱比，p為壓力，ρ為密度，超聲波在20°C的空氣中進行傳播時，速度約為343.59m/s。

2.2 測量風速基本原理

超聲波的發射與接收是通過超聲波傳感器（亦稱超聲波換能器或超聲波探頭）來完成的。而超聲波傳感器就是利用超聲波的特性研制而成的一種傳感器［4］，其主要由壓電晶片組成，收發獨立型的超聲波傳感器組工作時，一個傳感器發射超聲波，則對應的傳感器則負責接收超聲波。

由于空氣中傳播時順風與逆風方向傳播的速度不同，所以對于收發一體的超聲波傳感器，距離固定后，接收到發射波的時間也不同，形成一個時間差值，這個時間差值與待測風速具有線性關系［5］。

如圖1所示，設傳感器1到傳感器2的方向為風向，風速為V，超聲波傳播速度為Vu，傳感器距離為d，超聲波由傳感器1到傳感器2的傳播時間為t12，傳感器2到傳感器1的時間為t21，則有：

圖1 超聲波檢測風速原理

從式中可以看出風速的測量沒有包含影響風速測量的超聲波傳播速度Vu（不同環境下數值不同），即避免了溫度等其他因素對系統測量精度的影響［6］。

2.3 測量風向基本原理

如圖2所示，設兩對超聲波傳感器距離均為d，x軸方向的傳輸時間分別為t12和t21，y軸方向的傳輸時間分別為t34和t43，風速為V，x軸方向的風速分量為Vx，y軸方向的風速分量為Vy，超聲波傳播速度為Vu。根據式（1）可得：

圖2 二維正交陣列檢測風向原理

設x軸正方向為0°，角度按逆時針方向增大，則風向：

化簡并求反函數：

隨著風向的變化，可得某時刻風向為

當t12≤t21且t34≤t43，k=0 ；當t12＞t21且t34＞t43，k=1 ；當t12＞t21且t34＜t43，k=1 ；當t12＜t21且t34＞t43，k=2 ；

3 三維超聲波陣列三維風測量原理

根據超聲波測風基本原理知，一對超聲波傳感器可測得其所在直線上的風速，則三對超聲波傳感器經過一定設計可實現對三維風的測量。

3.1 建立三維風模型

如圖3所示，在空間直角坐標系中，y軸指向正東方向,為一個風速矢量，風速矢量的映射線與正東方向的夾角α為風向的水平偏角，風速矢量與水平面的夾角β為風向的垂直偏角，可以用風速大小、水平偏角α、垂直偏角β來表示三維風。水平偏角α的范圍為，垂直偏角β的范圍為為了便于計算模型的建立，本文規定(x,y,z)象限為正風向的象限［7］（以下公式中用V代表風速大小

圖3 三維風模型示意圖

3.2 超聲波測風設備垂直正交陣列設計

如圖4所示，垂直正交測風陣列中，有PP'、QQ'、RR'共計6個傳感器，每組所在直線分別對應空間坐標系的三個軸。L為每對傳感器中探頭之間的距離，三組傳感器所在的直線與空間直角坐標系的三條軸重合，其中，y軸指向正東方向，V為三維風［8］。

圖4 三維超聲波垂直正交測風陣列

3.3 時差法測風

將風速矢量沿著三個坐標軸正交分解為Vx、Vy、Vz，根據式（1），Vx、Vy、Vz的表達式如下：

根據正交分解原理，原始風速與分解風速之間的關系如下：

由式（11），結合式（8～9），實際風速歸一化公式如下：

由圖4，水平偏角α為風速矢量的映射線與正東方向的夾角，垂直偏角β為風速矢量與水平面的夾角，那么根據直角三角形勾股定理可知，水平偏角α只與水平分量Vx、Vy有關，垂直偏角β與垂直分量Vz以及水平分量Vx、Vy的合分量有關，其角度解析式如下：

3.4 傾角存在下的風速和風向值變化分析

1）風速變化情況

如圖5，當三維測風陣列相對于空間直角坐標系產生傾角，由立方體對角線理論知風速V不變，即：

圖5 三維垂直正交測風陣列傾斜示意圖

2）風向變化情況

傾角存在時，V在x'y'z'及xyz上的投影不同，故不能根據Vx'、Vy'、Vz'通過式（13）、（14）直接求得風向，需首先根據矩陣旋轉理論通過Vx'、Vy'、Vz'推導出Vx、Vy、Vz，而后可依據前述時差法測量三維風向方法計算出風向值。

4 二維超聲波陣列水平風測量方法研究

風主要是指空氣運動時的水平分量，風速是指空氣在單位時間內移動的水平距離，風向是指風水平吹來的方向，所以在超聲波測風技術的具體應用中，從成本考慮出發，多選用二維測風陣列用于對水平風的測量［9～11］。根據超聲波測風原理，二維測風陣列需保持水平狀態才能測得水平風場準確數據，陣列傾角對測量精度影響較大。為研究影響情況，現從三維坐標系傾角情況著手進行分析。

1）構建坐標系傾角模型

首先基于二維測風陣列構建直角坐標系，其中正交的超聲波傳感器分別與空間直角坐標系的x軸及y軸重合，對直角坐標系正直向上作垂直分量，構建陣列坐標系x'y'z'，與空間直角坐標系的z軸重合。傾斜使得二維陣列產生俯仰角θ、翻滾角φ及偏航角ω，如圖6所示。

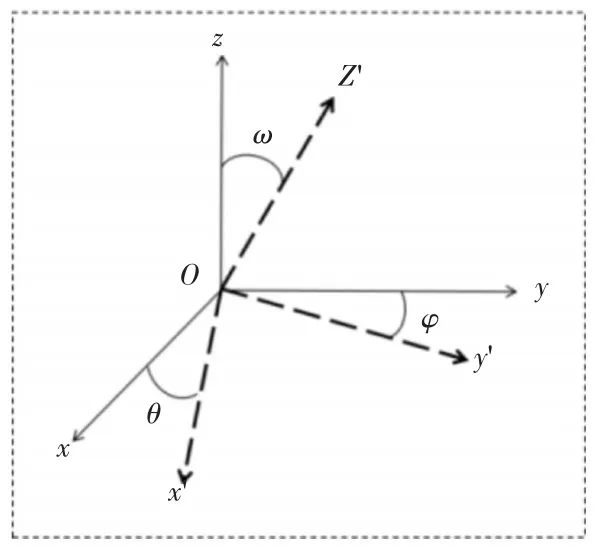
圖6 空間直角坐標系與陣列坐標系

2）三維坐標系旋轉矩陣

根據三維坐標系空間旋轉變換相關理論［12～13］，結合圖7，現規定從空間直角坐標系xyz到陣列坐標系x'y'z'的順序：先繞x軸旋轉φ，而后繞旋轉后的y軸旋轉θ，再繞第二次旋轉后的z軸旋轉ω，即每一次旋轉都是上一次旋轉的疊加。相應的，從陣列坐標系x'y'z'到空間直角坐標系xyz的順序剛按相反旋轉順序得到。其中最右圖中的x2y2z2即為x'y'z'。對于z，y，x方向的旋轉都是按照右手系定則：大拇指指向軸線方向，四指方向為旋轉的正方向。

圖7 三維坐標系空間旋轉變換示意圖

根據矩陣理論，從空間直角坐標系到陣列坐標系的旋轉矩陣有如下定義：

根據旋轉矩陣左乘原理，陣列坐標系到空間直角坐標系的旋轉矩陣為

設x'y'z'坐標系下測量值為（OA'OB'X），其中X為z'軸方向未知值，則其與xyz坐標系中各分量對應關系為

結合圖5，理論上，水平風速值OD由分解風速值OA及OB通過三角函數關系計算得出：

根據式（20）、（21）看出影響OD的因素主要包括θ、φ、ω及陣列垂直分量X的影響，其中θ、φ、ω取值由機載陀螺儀測得。

考慮到無人機通過自旋可以修正偏航角，本文提出首先根據機載陀螺儀測得的偏航值，通過使無人機自旋讓偏航值ω歸零；另外考慮到機體坐標系x'y'z'的垂直分量X未知，而理論上水平風速最大時，機體傾斜最大，基于此建立線性關系，對X進行賦值。本文主要對以下算法進行實驗驗證。

其中，?為機體姿態傾斜角，?max為機體的最大姿態角限幅，Vmax為旋翼無人機允許的最大水平風速，V為實際水平風速。

5 實驗結果與分析

本文實驗主要利用Matlab軟件對算法進行核算。關于X與OD的關系，主要從以下方面來考慮。

1）旋翼無人機的最大姿態角限幅

根據當前多旋翼無人機發展現狀，通用的無人機有效適飛風力等級一般為六級（10.8m/s～13.8m/s），最大姿態角限幅一般為20°，如圖8所示。

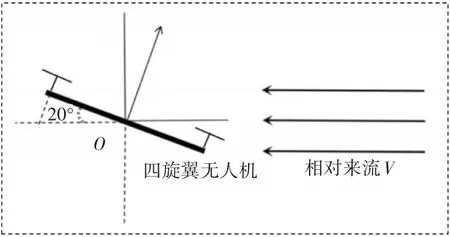
圖8 多旋翼無人機迎風傾角示意圖

2）實際應用領域對風場數據的測量范圍及精度要求

為某型固定翼飛機安全起降提供風場信息數據是多旋翼無人機超聲波測風系統的研究初衷，其要求系統的最大測風力范圍為13m/s，精度誤差小于0.5m/s。

根據如上信息，實驗中將最大水平風力Vmax設定為15m/s，測量精度0.5m/s，最大姿態角限幅?max為20°，偏航角ω的取值范圍0～45°，同時考慮到俯仰角θ、翻滾角φ同樣受最大姿態角限幅制約，為適當擴大測量范圍，規定θ、φ取值為實際傾斜值?，即二維正交陣列的兩測量值相等：

結合式（25）～（28），求取了風速計算值OD與給定風速值V之間的差值Δ，通過分析Δ以驗證算法可行性。將算法編程輸入Matlab軟件，隨著水平風速V及偏航角ω的增加，計算后得到一系列差值Δ相關數據，如表1所示。

表1 航角歸零及線性賦值算法誤差分析表

表1中，橫軸為給定水平風速值V，取值范圍為0～15m/s，縱軸表示偏航角ω，取值范圍為0～45°，其中V及ω的步長分別為1m和1°。

從表1中可以看出，未著色區域Δ值均小于精度值0.5m/s，淺色區域Δ差值在0.5～1m/s之間，深色區域Δ差值大于1m/s，以此得出在風速小于13 m/s且偏航角歸零情況下，計算水平風速值與給定水平風速值之間誤差在許可范圍內，風速值在13m/s～15m/s時，誤差小于1 m/s。

6 結語

本文針對傾斜情況下多旋翼無人機二維超聲波測風系統不能準確測量水平風場信息的問題，根據機載陀螺測得的數據，提出系統每次工作前需首先利用無人機自旋將偏航角歸零，同時對未知的垂直分量值通過線性關系進行賦值的方法，并結合軟件進行了實驗驗證。實驗證明，對于正交二維超聲波測風傳感器發生傾斜情況下，在一定的傾斜角度及風速范圍內，根據旋轉矩陣理論，可以通過偏航角歸零及給垂直分量線性賦值的方式，近似求出水平風速值，但也存在由于搭載的無人機平臺需自旋使偏航角歸零后，測得的數據才可用于計算，故風速識別周期較長的缺點，但此方法能夠保證測量精度基本滿足實際的需要，具有一定的實用價值。