基于分布式聚類的制造業大數據監測與分析算法

張路

（臺州職業技術學院經貿學院，浙江臺州 318000）

隨著我國制造業發展的不斷創新，智能制造的應用逐漸普及。國家綜合實力的重要提升手段，即是本國制造業的迅速發展。制造業大數據作為生產過程的重要要素，能在較大程度上推動制造業的升級轉型[1]。

大數據分析是評估各種數據集以發現模式、相關性、市場趨勢和其他有用信息的技術手段，可以幫助相關部門作出更明智的決策[2]。大數據算法需要與實際數據共同發揮作用，此外，在智能車間使用智能制造對象的RFID 數據的相關研究也較少。為了彌補這些不足，該文針對制造業RFID 大數據使用分布式聚類算法建立了監測與分析的算法架構。

1 大數據監測分析算法架構

RFID 數據來自具有物聯網功能的制造車間。當操作人員使用閱讀器對標簽進行檢測或對RFID閱讀器進行操作時，系統將記錄一條RFID 數據。其數據集定義如表1 所示[3]。

表1 RFID數據集定義

數據記錄員通過操作這些數據集可以計算出以下主要變量：一種是在一段時間內跟蹤特定的BatchMainID，然后對比批處理所需的時間。一種是UserID 和ProcCode，用于觀察操作員在車間的操作效率，最后，通過跟蹤每個BatchMainID 以獲得完成制造批次所需的操作員數量，對于制造業數據分析也有較為重要的意義。

此次所提出算法方案的工作流程如圖1 所示。該體系結構涉及4 個主要過程：數據預處理[4]、分類、模式識別和可視化[5]。從制造車間的大量RFID 數據生成有關制造工廠生產效率的信息可視化視圖，這些相互獨立的數據集群為預測提供線性或非線性回歸數據。

圖1 算法流程

1.1 數據預處理

原始RFID 數據沒有TimeFloat 數據代碼，因此在將數據導入TensorFlow 程序時，需要將其修改為正確的格式。原始RFID 數據時間按照連續的日、月和年格式（DD/ MM/ YYYY）排列，該算法只支持使用數字類型（例如整數或浮點數），因此程序無法直接使用該數值。此外，為了方便計算，閏年的影響忽略不計[6]。

此次實驗用的RFID 數據集總共包含413 472 個數據。考慮到BatchMainID 的完成時間，需要對制造業數據的時間信息重點分析。因此為了提高處理速度，所有沒有時間條目的數據均被刪除[7]。經過初步篩選的數據為376 746 個條目，但這些條目是從制造車間的高集成度傳感器中收集的，且信息量不足。通過對數據采用線性回歸和質心比較法[8]，進一步篩選有用數據至176 746 個。

1.2 批次識別算法實現

此次通過使用BatchMainID 與時間之間的關系進行數據分析，以產生具有統計意義的相關數據，實現對制造數據批次的識別[9]。

圖2 顯示了匹配的BatchMainID 進程與時間的所有176 746 個樣本的繪圖。樣本數據較集中，因此難以識別隱藏的模式或趨勢。另外，整體數據的計算成本較高。因此可以得出結論：數據集聚類分析是算法設計的重難點問題[10]。

圖2 BatchMainID與時間關系圖

此次通過跟蹤各個BatchMainID 以獲取開始時間和結束時間，并計算完成批處理的進程數量[11]。文中使用的分布式機器學習聚類方法是有監督和無監督學習過程的集成，首先使用K-means 聚類（一種無監督的學習方法）將數據分組為多個聚類[12]。然后使用梯度下降優化算法（一種有監督的學習方法）來計算預測值，并減少成本與目標函數的損失[13]。

2 分布式聚類算法設計

K 均值聚類算法核心為分布式思想，該過程從數據集和一組隨機聚類中心開始。在每個迭代過程中，將每個元素分配給其最接近的集群[14]，這樣的設計能夠在基于單個處理器的傳統計算機上良好地運行。傳統的集中式K 均值算法在使用計算機求取聚類結果時，要用到所有需要聚類的數據[15]。在數據量較大的應用場景下，集中式聚類服務器難以達到效能要求，因此提出了分布式的聚類算法。分布式聚類服務器通過Internet 網絡連接實現通信，各個站點僅計算部分信息。分析數據根據就近原則存儲在網絡的不同站點上，聚類結果通過網絡通信協議相互影響[16]。分布式K 均值聚類算法的關鍵問題是協調各個站點之間的數據計算，即全局中心計算問題，這與集中式K 均值數據分析方法有本質的區別。該文提出了一種針對解決全局中心計算問題的算法，以實現大數據下分布式K 均值中心算法的設計。下面將詳細描述改進的分布式聚類算法的實現過程：

每個處理器Si根據站點的制造業數據，初始化一組任意的聚類中心向量Mi={mk|k=1,2,…,K}。每個站點相互獨立地計算數據中心點，在設計的分布式算法的每次迭代步驟中，本地站點Si將計算得出的聚類中心通過UDP 通信協議廣播到通信網絡中。在本地站點上聚類后，所有聚集的本地數據和估計的中心點矢量均將作用于；而新的中心點矢量將被計算并記錄為。在每次迭代產生新聚類中心的過程中，為了避免站點聚類結果出現空集，迭代過程中的估計中心點被添加至聚類數據中。

中心計算是設計的分布式聚類分析算法的最重要特征。為闡述集中式與分布式聚類算法的核心區別，可用式（1）與式（2）說明，集中式K 均值可表達為：

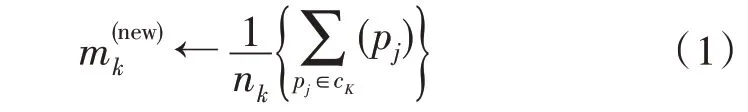
分布式K 均值可表達為：

每次迭代產生的新中心向量以廣播方式存儲在所有站點上。每個站點Si根據本地數據計算所得的聚類中心值和從其他站點收到的聚類中心值，根據加權平均法得出新的中心值，并替換。分析可知，聚類服務器除去在迭代第一步可能出現空集的情況外，所有站點在所有的迭代步驟中均可確定唯一的聚類中心。通過上述步驟，即可實現聚類中心向量范數穩定，直至聚類結束。

由于數據規模與通信的要求，分布式數據監測與分析對于計算機性能有較大的考驗。為了檢測算法對于計算機資源的要求，對分布式K 均值算法的復雜度進行分析。對于任何并行和分布式聚類算法，復雜度均有兩個方面，即時間復雜度Ttime和通信復雜度Tcomm。在通信過程中，數據、中心向量等相關信息需要從一個站點傳輸到另一個站點。首先分析一個迭代步驟中分布式聚類算法的復雜度，處理站完成一項聚類后，實際通信時間定義為Tdata；服務站與通信網絡建立通信連接所需的時間定義為Tstart。由于數據傳輸是并行執行的，因此僅傳輸一個數據，每一步的復雜度為：

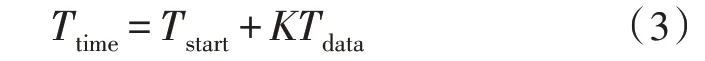
計算距離的復雜度為：

Tdist是處理站計算處理單個制造業數據的時間；設計的分布式分析算法復雜度可由式（5）得出：

式中，T為網絡中聚類算法的迭代次數。

忽略處理器間的連接時間，算法復雜度可用以下形式表示：

從上式可以看出，時間復雜度不僅包含TKTdist，且包含本地站所有數據矢量的計算、本地站點元素數量分配、所有本地站點的歐幾里德最小二乘誤差計算以及通信復雜性。算法復雜度僅呈線性增長，可用于大范圍部署。

3 實驗驗證

為驗證該系統的有效性，使用基于RFID 的制造業大數據進行算法驗證。

預測算法的結果如表2 所示。輸入是一維數組，該數組描述了進程數；輸出為這些進程與集中處理器的分配方式。預測百分比表示了分配的準確率，可以看出該方法比計算預測更可靠。

表2 預測結果

通過5 次獨立進行的實驗操作，取每個樣品的平均數作為計算成本來驗證實驗結果，如圖3 所示。

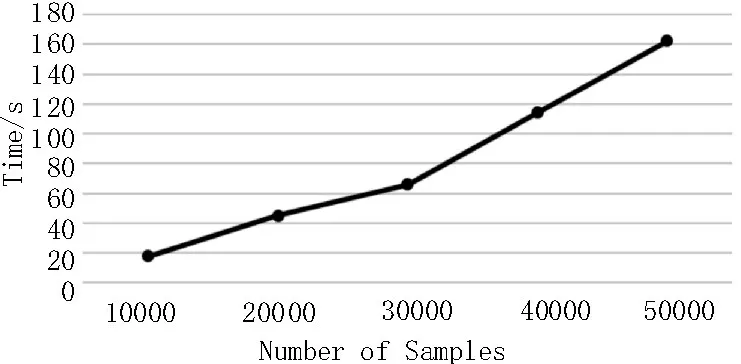
圖3 計算成本實驗

可以看出，隨著樣本數量的增加，計算時間成本也在增加。由于該算法進行數據預處理、可視化和優化需要花費時間，因此實驗結果是合理的。為排除大數據中的錯誤并對不確定性數據進行處理，計算成本實驗使用了高達10 000 個樣本。由于算法內產生的是隨機數（例如權重、常數和預測輸入值），即使樣本數相同，每次運行的計算成本也不同。但從圖3 可以看出，綜合統計成本下，計算成本與樣本數呈線性關系，并未由于數據量的增長而造成成本的顯著上升。

實驗使用的處理服務器為2.50 GHz 的Intel?Core?i7-6500U CPU。測試可知，若該算法在NVIDIA GPU 支持下進行數據分析，則可降低計算成本，因為TensorFlow 程序在GPU 上的速度明顯快于CPU 處理速度。

為了測試該算法的多平臺運算能力，在CPU（Intel i7-6700）的計算平臺上，采用3 種具有不同功率水平的GPU 和基于DSP 的處理器（Intel Movidius）進行了聚類算法測試，實驗結果如圖4 所示。使用的GPU 是NVIDIA Jetson TX2 的Max-Q 與Max-P，分別標記為GPU＃1和GPU＃2，GPU＃3為NVIDIA Tesla V100。顯然，GPU＃3 在處理速度上優過其他類型的處理器，而其相應的最大功耗明顯大于其他處理器。

圖4 跨平臺測試實驗

在驗證算法分析準確率與成本的基礎上，通過引入不同類型的樣本數據以進一步評估算法的表現。由于計算量大，僅將前10 000個樣本生成的模型與最終選擇的樣本進行比較。根據經驗可知，分析超過10 000 個數據大小會產生較高的計算成本。同樣，繪制的數據越多，可見性的質量就越差。

圖5 為10 000 個樣本的分類散點圖，其描述了最近10 000 個樣本的聚類結果。分析圖5 可以看出，該算法對于生產數據可以精確地分為不同的類型，準確率可達98.9%以上，算法對預處理的制造業大數據聚類時間僅為13.2 s，具有較好的實時性。

圖5 樣本分類散點圖

4 結論

該文設計了一種大數據分析方法，用于檢測與分析來自制造業的大量RFID 數據。該方法包括了數據的處理和可視化，并對其進行了綜合驗證和評估，得到結論如下：1）可以直接對從制造現場獲取的大數據進行分析，以作出預測并提高效率；2）提出了梯度下降和聚類方法的組合。當使用大量樣本對算法進行測試時，將損失降至合理的水平。

今后的工作重點將放在如何在移動終端中實現分析的可視化，以便于用戶訪問。此外，算法商業化則需要考慮軟件設計原理，以提高所提出方法的可讀性、可擴展性、有效性和數據處理效率。