基于分數階微積分的圖像去噪算法研究

徐艷華

（陜西鐵路工程職業技術學院，陜西渭南 714000）

目前，分數階微積分在科學、工程等眾多領域得到了迅速的發展，因此任意階微分方程在物理、流體力學、生理學、工程、勢理論、彈性力學等領域得到了廣泛的研究[1-2]。近年來，將微積分應用于圖像處理已成為一個熱點研究課題，并有大量的研究成果發布[3]。與整數階微積分相比，在圖像去噪過程中，分數階微積分方法可以在保留平滑區域細節信息的同時增強邊緣，使紋理更加清晰。

傳統的分數階微積分方法對圖像邊緣、紋理和平滑區域采用相同的階數處理。當使用高分數階來處理圖像噪聲時，弱紋理和平滑區域將被忽略，而使用低分數階會削弱圖像的邊緣[4]。因此在實際應用中，僅使用整數分數階微積分對圖像的去噪效果并不理想，進而提出了基于分數階微積分的圖像去噪算法。該算法利用圖像梯度特征構造分數階微積分算子，采用不同的分數階對不同的像素進行處理，從而實現圖像去噪[5]。

1 分數階微積分理論分析

1.1 分數階微積分

根據傅里葉變換的基本理論，將圖像信號處理定義為：

式 中，Dγ為γ階微分算子，ω為角頻率，為分數階微積分濾波器的濾波函數，sgn(?)表示整數部分的數字符號。

在頻率特性方面，分數階微積分利用Gamma 函數Γ(t)t將其定義擴展到分數階，Grumwald-Letnikov（GL）定義的γ階分數階微積分為：

式中，[?]表示整數部分，信號的持續時間f(t)為[a,t]，a是任意實數，表示由GL 定義的γ階分數微積分算子。當γ＞0 時，是γ階的分數微分算子；當γ＜0 時，是γ階的分數積分算子。

分數階微積分的頻率響應如圖1 所示。

圖1 分數階積分的幅頻特性曲線

由圖1（a）可知，隨著分數階微分階次和頻率的增加，對于高頻信號的增強作用也明顯增加，且增強的幅度在后期最為明顯。由圖1（b）可知，隨著分數階積分階次和頻率的增加，分數階積分運算對高頻信號的衰減幅度也逐漸增加。

由此可知，分數階微分可增強、保留圖像邊緣和紋理特征，而分數階積分則可以去除圖像噪聲。

1.2 分數階微積分對圖像的處理

在二維數字圖像中，相鄰兩個像素之間是灰度變化的最短距離，因此圖像在x軸和y軸方向上的持續時間只能以像素為單位來測量[6]。因此根據GL 分數階微積分表達式，可以得到信號f(t)的γ階為：

根據信號f(t)的γ階分數積分表達式，對于任何函數f(x,y)∈L2(R2)，求出γ階偏微積分關于x和y的微分表達式，因此可得到5×5 分數積分掩模，如圖2 所示。

圖2 分數積分掩模

掩模是在8 個方向上疊加部分分數階積分得到的，是旋轉不變的。式中，w1、w2和w3分別為第一、第二和第三系數，且w1=1、w2=-γ、w3=(-γ)(-γ+1)/2。此時，通過考慮該掩模卷積的空域濾波，可以得到用γ階分數積分處理的圖像。

2 圖像去噪算法

2.1 噪聲類型

在圖像中，各類別的噪聲一般劃分成兩種典型的噪聲：椒鹽噪聲和高斯噪聲[7]。

椒鹽噪聲由不完善的開關設備產生，通常產生于圖像傳感器、解碼處理或圖像切割等[8-9]。該噪聲出現位置為隨機位置，但幅值基本相同。

對于圖像的每一個像素點，均存在高斯噪聲，其概率密度函數為：

其中，z為灰度值，u為期望值，σ為標準偏差，σ2為方差。

2.2 噪聲判別

圖像邊緣和紋理豐富區域的梯度較大，平滑區域的梯度較小[10-11]。圖像u0(x,y)的像素(x,y)處的梯度可表示為。梯度模值公式為：

圖像的邊緣是連續的，據此構造出噪聲邊緣的判別函數：

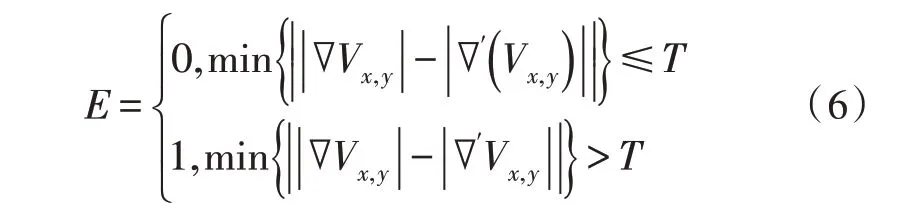
式中，|?Vx,y|與|?′Vx,y|分別是中間和附近區域像素點的梯度模值。

2.3 基于分數階微積分的圖像去噪

在圖像去噪過程中，需要將噪聲點與紋理區域區分開[12-13]。將圖像出現噪聲點作為一個小概率事件，結合局部特征來分割各個區域，并使用3×3 區域來分析圖像結構信息。

最小絕對灰度距離為：

式中，I(P)是像素P的灰度值，P和Pi是像素。

在圖像的8 個方向上，圖像邊緣多為連續像素[14-15]，因此最小絕對距離ADmin較小。假設當前像素u0(x,y)中，8 個方向上每個方向的灰度距離平均值為M(x,y)，則：

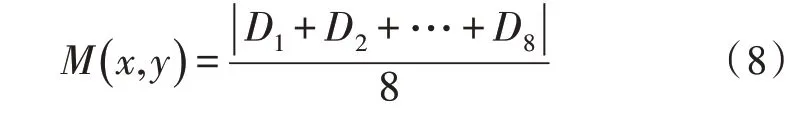
選擇分割后的噪聲點最小值M(x,y)作為圖像噪聲點的閾值T。當M(x,y)≥T時，將對應的像素(x,y)視為噪聲點，該值越大，噪聲越強。在圖像去噪過程中，應將階數γ取為負值，且階數的大小與M(x,y)的值有關[16]。通過選擇一個自適應分數階，當噪聲較大時，自適應積分階數將變小、灰度幅值將衰減。

當1 ＜M(x,y)＜T時，對應的像素(x,y)被視為邊緣或紋理區域的一個點，在去噪過程中分數階微分階數應取正值。階數的大小與M(x,y)和計算熵EN(x,y)有關，則通過選擇一個自適應分數階。

當0 ≤M(x,y)＜1 時，將像素(x,y)視為平滑區域中灰度值不變的一點。

3 實驗結果及分析

基于Matlab R2012a 軟件對所提算法進行仿真實驗，其中計算機的硬件配置：CPU 為2.40 GHz Intel Core i7，RAM 容量為4 GB。

對于一種圖像去噪算法，通常采用峰值信噪比（PSNR）來評價去噪效果及其綜合性能。PSNR 值越大，算法的去噪效果越優。峰值信噪比定義為：

式中，原始圖像的大小為M×N，u0(i,j)表示原始圖像，un(i,j)表示去噪后的圖像。

3.1 可視化分析

實驗中使用的圖像大小為256×256，具有不同紋理的莉娜和船舶圖像。設定λ1=0.4、λ2=0.6，取噪聲平均值作為實驗噪聲強度。將所提算法與文獻[9]、文獻[10]、文獻[12]中去噪算法得到的圖像進行可視化對比，結果如圖3、圖4 所示。

圖3 不同算法對含噪莉娜圖像的去噪效果

圖4 不同算法對含噪船舶圖像的去噪效果

從圖3 和圖4 中可以看出，文獻[9]采用迭代空間屏蔽的去噪方法，對于椒鹽和高斯噪聲的去噪效果不理想；文獻[10]在保持圖像邊緣細節方面表現較好，但在去噪效果上仍有所欠缺；文獻[12]在消除所有噪聲的同時也丟失了圖像中大量的細節信息，圖像的邊緣和細節紋理區域產生了模糊化，去噪效果有待提高。傳統的順序使圖像模糊，同時使圖像亮度降低。而所提算法去噪后的圖像，既能較好地去除噪聲，又保持了帽檐等邊緣細節信息[17-18]。

3.2 去噪效果定量分析

此外，對所提算法的去噪性能進行定量分析。4種不同算法的PSNR 比較結果如表1 所示。

表1 各噪聲圖像經算法處理后的PSNR

從表1 中可以看出，不論是對椒鹽噪聲還是高斯噪聲，所提算法的PSNR 均高于其他對比算法，分別為30.470和25.653。文獻[9]由于依賴于空間信息，因此去噪效果不理想；文獻[10]利用改進的曲率濾波進行圖像去噪；而文獻[12]在此基礎上結合了小波變換，因此去噪效果有所增強，分別是25.566和24.462。

4 結束語

該文提出一種基于分數階微積分的圖像去噪算法。基于分數階微積分對圖像處理進行了理論分析，結合局部結構劃分噪聲點、邊緣、紋理區域和平滑區域構造了一個分段函數，以實現對不同區域像素的去噪處理。此外，基于Matlab 仿真平臺對所提算法進行實驗論證。結果表明，所提算法PSNR 均高于其他對比算法，在椒鹽噪聲和高斯噪聲中PSNR 的值分別為30.470 和25.653，且能在去除噪聲的同時保持圖像邊緣和紋理特征。在后續研究中，將聚焦解決如何與其他的一些經典去噪算法相結合以得到更優的去噪效果。