貝葉斯最優多階段Ⅱa期自適應臨床試驗方法-BOP2設計

謝婉秋, 周 影， 郭東升

(1.黑龍江大學 數學科學學院, 哈爾濱 150080; 2.哈爾濱金融學院 投資保險系, 哈爾濱 150030;3.科臨達康醫藥生物科技(北京)有限公司 生物統計與編程部門, 北京100026)

0 引 言

Ⅱ期臨床試驗的目的是評估新療法的初步療效，并確定這種療法是否有進行大規模的Ⅲ期隨機對照臨床研究的研發前景[1]。其中Ⅱa期臨床試驗的基本設計特征是早期無效終止和中期go/no-go決策，防止過多的患者暴露在可能無效的治療中[2]。已經有眾多的頻率設計和貝葉斯設計應用于國內外Ⅱa期臨床試驗[3-12]。目前國內的臨床研究中，尤以著名的頻率設計Simon兩階段設計應用最為廣泛[13-14]，它在治療是無效的原假設下，給定Ⅰ類和Ⅱ類錯誤率，可最大程度地減少期望的樣本量或最大樣本量。如果想多做幾次中期觀察，統計師也可參考其他相關研究包括Fleming的多階段檢驗[15]、Ensign的最優三階段設計[16]和Chen的最優三階段設計[17]等。

另一面，以貝葉斯設計的觀點來看，無效監測的一種方式是基于感興趣事件的后驗概率做出go/no-go的決策。Thall等基于這種思想，提出了一種貝葉斯Ⅱa期設計，如果中期數據表明治療的緩解率有很高的概率小于預先指定的臨界值，則終止試驗；否則進入下一個中期觀察。此方法原理直觀，已在美國MD Anderson等癌癥中心廣泛使用[18]。在后驗概率的基礎上，Heitjan提出使用“說服概率”判斷新療法是否具有研發前景[19]。Tan等提出了兩個貝葉斯兩階段設計，他們模擬了頻率學派的多階段設計[20]。Cai等提出可以通過使用多重插補方法處理延遲的療效結局[21]。Lee等提出了另外一種基于預測概率的貝葉斯Ⅱa期設計，可以根據任意時刻的中期數據對最終數據進行預測并計算最終試驗成功的概率[22]。然而，以上無論基于后驗概率還是預測概率的設計大都集中在一個二元療效終點，如客觀緩解率，但隨著新型分子靶向藥物和免疫療法的出現，主要終點變得更加復雜，可以是有序的或多變量的[23]。

以下列舉了常見的四種不同類型終點的Ⅱ期試驗，BOP2設計將采用統一的模型處理以下Ⅱ期設計。

例1. 二元療效終點：一個Ⅱ期臨床試驗，目的是評估二甲雙胍在復發性小細胞肺癌患者的療效[24]。主要終點是ASO治療復發性SCLC患者的客觀緩解率(ORR)(使用RECIST1.1版[25]定義)。根據歷史數據，原假設ORR≤5%，成立則認為治療無效，備擇假設ORR≥20%，成立則認為該療法具有研發前景。該示例用于說明具有二元療效終點的標準情況。

例2. 嵌套的療效終點：一個Ⅱ期臨床試驗，目的是評估一種新型人源化單克隆抗體對自體干細胞移植后失敗的霍奇金淋巴瘤患者的療效。采用修訂后的《國際惡性淋巴瘤工作組標準》[26]定義淋巴瘤治療的有效性，從四種降低水平分類中選取一種，包括完全緩解(CR)，定義為所有疾病證據的消失；部分緩解(PR)，定義為可測量病灶的消退，沒有新病灶；疾病穩定(SD)，定義為未達到CR、PR或疾病進展(PD)的標準；疾病進展(PD)，定義為任何新病變的證據或病變體積從先前受累部位的最低點增加了50%。在該試驗中，盡管CR和PR均被認為是有利的療效反應，但實際上CR更可取。原假設是Pr(CR+PR)≤30%且Pr(CR)≤15%，成立則認為治療無效。備擇假設Pr(CR+PR)≥50%或Pr(CR)≥25%，成立則該認為該療法具有研發前景，其中第二種條件的終點嵌套在第一種條件終點中。

例3. 共同多療效終點：一個Ⅱ期臨床試驗，方案名為GOG 0229E，主要目的是研究貝伐單抗對復發或持續性子宮內膜癌患者的療效。該試驗有兩個共同的主要療效終點：客觀緩解率(ORR)和6個月無疾病進展(或死亡)生存的概率(PFS6)。客觀緩解率使用RECIST 1.1[25]定義。無進展生存期(PFS)定義為從治療開始到發生疾病進展或任何原因死亡的時間。原假設是ORR≤10%且PFS6≤15%。成立則認為治療無效。兩個指標在臨床顯著改善的差異為20%，所以備擇假設ORR≥30%或PFS6≥35%，成立則認為該療法具有研發前景。

例4. 聯合監測療效和毒性終點：一個Ⅱ期臨床試驗，主要目的是評價低劑量氯法拉濱和阿糖胞苷聯合治療復發或對低甲基化藥物不敏感的高危骨髓增生異常綜合征患者的療效[27]。主要療效終點是使用2006年修正的國際工作組標準定義的CR率聯合監測治療的安全性，以與研究藥物相關的3級毒性率作為聯合終點。原假設是CR率≤20%或毒性率≥30%，成立則認為治療無效。如果CR率>20%且毒性率<30%，則認為該療法具有研發前景。

本文重點介紹Zhou等2017年提出的一種靈活的貝葉斯最優Ⅱ期(BOP2)設計，該設計能夠處理上述試驗場景[1]。BOP2設計使用Dirichlet-多項式模型處理不同類型的終點。在每個中期階段，通過評估事件的后驗概率來做出go/no-go的決策。BOP2設計可精確控制Ⅰ類錯誤率，在某種意義上是最優的，包括在固定樣本量的備擇假設下優化檢驗效能或在原假設下最小化期望樣本量。Thall等提出了針對多主要終點(例如毒性和療效)的貝葉斯序貫監測設計[28]。與這些設計相比，BOP2設計具備更多的優勢，包括：(1)提供一個更靈活的框架來同時監測多個事件，包括嵌套或共同主要終點；(2)精確控制Ⅰ類錯誤率并優化特定的目標函數，從而彌補貝葉斯設計與頻率設計之間的差距，使所提出的貝葉斯優化設計更易于為廣大用戶和監管機構所用；(3)模擬研究表明，允許終止規則的臨界值隨中期樣本量發生變化，從而提高設計的檢驗效能。

本文第1節詳細介紹BOP2設計的概率模型，描述了試驗設計和設計參數的優化；第2節實際臨床試驗案例分析，同時簡要介紹www.trialdesign.org網站實現BOP2設計的軟件操作；第3節采用模擬方法比較BOP2與其他貝葉斯Ⅱ期設計的優勢，最后給出結論。

1 方 法

1.1 概率模型

盡管上述四個試驗案例的主要終點采用不同的形式，但可以統一由服從多項式分布的隨機變量X和K個類別表示：

X～Multinom(θ1,…,θk)

(1)

式中θk=Pr(X=k)是X屬于第k個類別的概率，k=1,…,K。K個類別可以是單個終點的真實級別，也可以是多個真實類別終點的某種組合。如例1中單個二元療效終點，多項式的分類K=2(OR，無OR)。例2中，X是有序結局指標，X=1,2,3和4分別表示CR，PR，SD和PD。例3中，X是具有4個類別的多項式變量：1 =(OR，PFS6)，2 =(OR，無PFS6)，3 =(無OR，PFS6)和4 =(無OR，無PFS6)。例4中，X是具有4個類別的多項式變量：1 =(毒性，CR)，2 =(無毒性，CR)，3 =(毒性，無CR)和4 =(無毒性，無CR)。

例1中N次抽樣(即N個患者參與試驗)，X為緩解的人數，服從二項式分布；類似的，例2、3、4將試驗結局分為4組，4組中結局發生對應的概率分別為θ1,θ2,θ3,θ4，且θ1+θ2+θ3+θ4=1；用(X1,X2,…,Xn)分別表示N個患者中每個結局組的人數，則X=(X1,X2,…,Xn)服從多項式分布，可見例1為例3的特例，如果例3忽略PFS6，多項式分布則退化為二項式分布。

設b表示由元素0和1組成的設計向量，而在以上4個示例中中期觀察的有效性可以表示為模型參數θ=(θ1,…,θk)T的線性組合：bθ≤φ或bθ≥φ，其中，φ代表預先指定閾值。

具體例1中，H0:bθ≤φ，其中b=(1,0)，φ=0.05；例2和例3中，H0:b1θ≤φ1且b2θ≤φ2，其中例2中b1=(1,0,0,0),b2=(1,1,0,0),φ1=0.15,φ2=0.3；例3中b1=(1,1,0,0),b2=(1,0,1,0),φ1=0.1,φ2=0.15；例4中，H0:b1θ≤φ1或b2θ≥φ2，其中b1=(1,1,0,0),b2=(1,0,1,0) ,φ1=0.2,φ2=0.3。以上結果匯總在表1中。

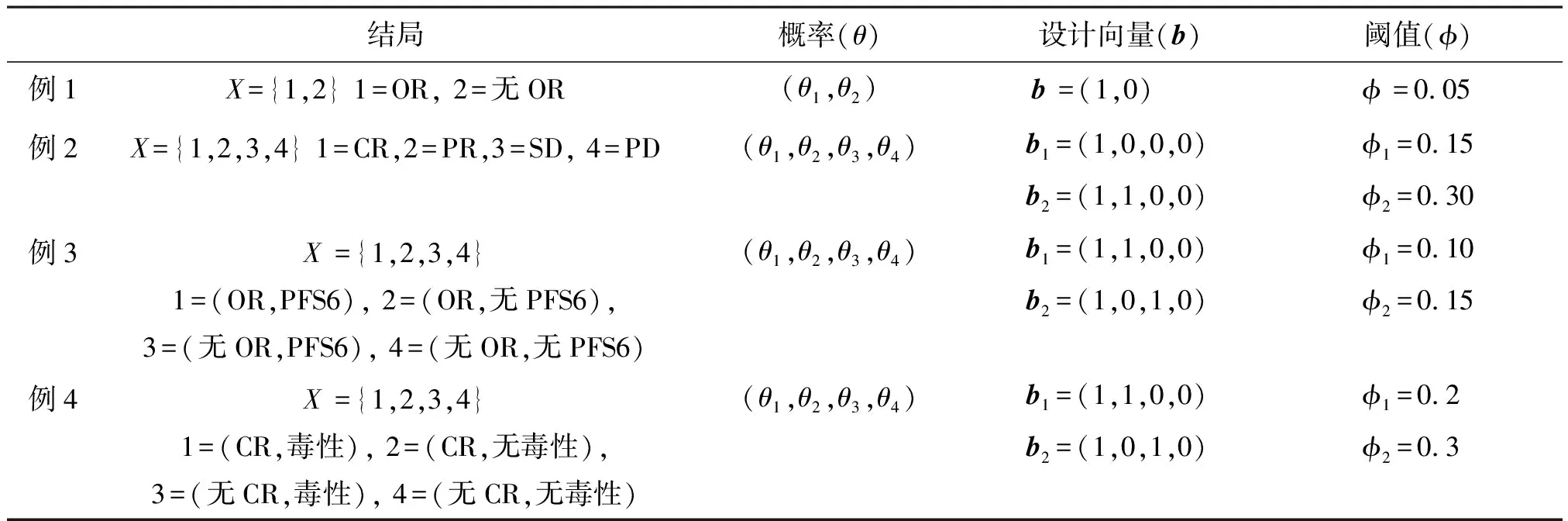
表1 四個試驗案例的結局及參數設置Table 1 Outcome and parameter setting of four trail cases

在貝葉斯的框架下，通常為了方便推導參數的后驗分布，會先假設參數的先驗分布是聯合似然函數的某個共軛分布，故假設θ=(θ1,…,θk)T服從Dirichlet共軛先驗分布：

θ～Dirichlet(α1,…,αK)

(2)

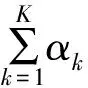
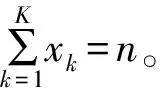
θ|Dn～Dir(α1+x1,…,αK+xK)

(3)

在X是二元結局的特例中(例1)，該Dirichlet-多項式模型退化為標準的Beta-二項式模型。

1.2 試驗設計

設N代表試驗的最大樣本量。BOP2設計包括R個中期觀察，當納入的患者人數達到n1,n2,…,nR時，以及所有N個患者都納入后的最后一次觀察。如下文所述，每一次中期觀察的目的包括評估新療法是否具有研發前景或者由于目前試驗累積的數據不足以支持任何結論而需要納入更多的患者。換言之，患者分別納入到大小為n1,n2-n1,…,N-nR的R+1隊列中，并在每個隊列入組后做出go/no-go的決策。當R=N-1時，獲得了一個完整的序貫設計，在每個患者之后都會連續評估go/no-go決策。

設C(n)表示概率閾值，它是中期樣本量n的函數。在這個設計中，每個中期階段的go/no-go決策都是基于事件的后驗概率來進行的。具體地，對于四個試驗案例，在中期觀察后，如果出現以下情形則終止試驗：

例1： Pr(θ1≤0.05|Dn)>C(n)；

例2： Pr(θ1≤0.15|Dn)>C(n)且Pr(θ1+θ2≤0.3|Dn)>C(n)；

例3： Pr(θ1+θ2≤0.1|Dn)>C(n)且Pr(θ1+θ3≤0.15|Dn)>C(n)；

例4： Pr(θ1+θ2≤0.2|Dn)>C(n)或Pr(θ1+θ3≥0.3|Dn)>C(n)。

與大多數現有的貝葉斯設計[18,28]假定一個恒定的臨界值不同，BOP2設計的作者們允許概率閾值C(n)是中期樣本量n的函數。就像優化參數設計中展示的內容，這種修改可以大大提高設計的檢驗效能，是BOP2設計的點睛之筆。盡管這些停止規則在臨床上有不同的解釋，但是go/no-go決策都是可歸結為基于對模型參數θ=(θ1,…,θk)T的線性組合的后驗概率為評估基礎，例如，

Pr(bθ≤φ|Dn)>C(n)

(4)

式中b是元素為0和1的設計矢量，φ是預定閾值。

Dirichlet分布有兩個特性有助于對(4)中的后驗概率進行評估。

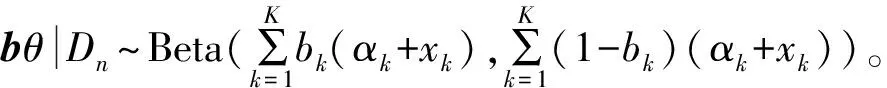
因此，可以將Pr(bθ≤φ|Dn)很容易地評估為

式中B(φ;ζ,ξ)是含有參數ζ和ξ的Beta分布的累積分布函數，并評估值φ。Pr(bθ≤φ|Dn)的性質導致以下結果。

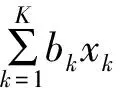
性質1和引理1的證明和解釋過程見附件1。在實踐中，Pr(bθ≤φ|Dn)的單調性很重要，由于單調性，不需要在搜索網格中的每一個點上執行實時計算，可在試驗開始前，通過單調性來計算停止邊界，這類似于Simon的兩階段設計。表2展示了在控制Ⅰ類錯誤率10%，已知最大樣本量40，最大化檢驗效能的條件下，四個試驗案例的停止邊界。如例1中25例患者入組以后，如果緩解的患者數≤1則終止試驗，判斷新療法沒有研發前景；例2中，納入25例患者后，如果CR人數≤4且CR+PR人數≤8則終止試驗，判斷新療法沒有研發前景。這個過程不需要任何復雜的計算，僅需計算相關的事件數，便可以做出go/no-go的決策，表2中數據可以在www.trialdesign.org網站獲得，僅需輸入幾個簡單的參數。這個屬性使BOP2設計在實踐中非常容易實現。

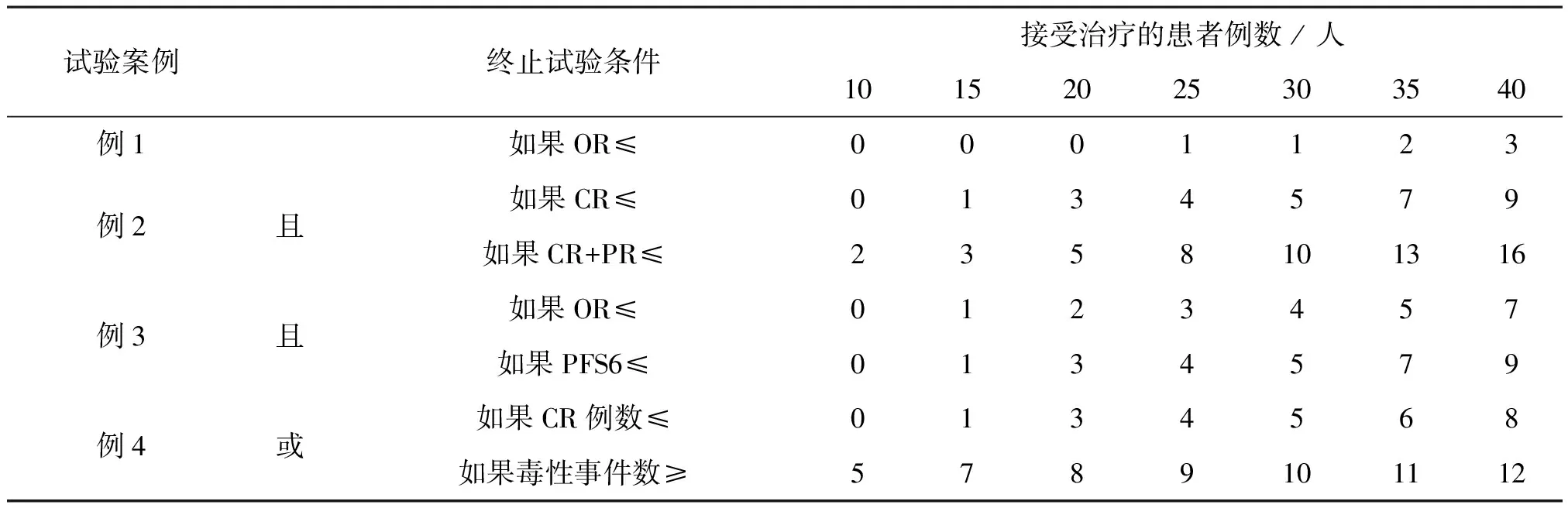
表2 四個試驗案例的BOP2設計的停止邊界值Table 2 Stop boundary value of BOP2 design of four trail cases

1.3 優化設計參數

首先，本設計需根據相關試驗背景選擇適當的原假設H0和備擇假設H1，依據反證思想，原假設為希望依據數據拒絕的假設。原假設表示的θ認為該方法無效，而備擇假設為希望得到的結論，即表示的θ認為該療法有研發前景。Ⅰ類錯誤率和統計檢驗效能分別定義為在H0和H1下拒絕H0的概率，Ⅰ類錯誤率是指藥物無效的原假設為真時拒絕原假設的概率，應使其得到有效控制即保證患者風險最小化;統計檢驗效能是指該療法具有研發前景的備擇假設為真時拒絕原假設的概率，應盡量在控制風險的前提下最大化檢驗效能以保證新藥申辦者的利益。如例2中，H0：θ1≤0.15和θ1+θ2≤0.3，一個可能的合理備擇假設是H1：θ1≥0.25或θ1+θ2≥0.5。對于這種復雜的終點，H0和H1的預定閾值應通過與臨床醫生協商確定，用來反映在臨床實踐中可行的理想結果。未拒絕H0意味著試驗結果未達到最低臨床有效邊界值，則該療法無效，不具有研發前景。

與大多數貝葉斯設計假定一個恒定的臨界值不同，BOP2設計的點睛之筆在于指定的一個概率閾值是中期樣本量n的函數C(n)，這種修改可以大大提高設計的檢驗效能。C(n)可以使用任何靈活且合理的單調遞減函數，但采用如下兩參數冪函數可以具有良好的特性：

C(n)=1-λ(n/N)γ

(5)

其中λ和γ是調整參數。要求γ> 0，以便C(n)隨著n/N單調遞減，這樣設計的優點是試驗開始時數據比較稀疏，停止規則較為嚴格，避免意外終止，隨著越來越多的數據積累，對目標終點的不確定性越來越小，停止規則自適應地變得更加寬松。為獲得最優解，BOP2提出者設定了兩種方式優化準則，在各類限制條件下的所有解中選取最合適的一組。

1.3.1 固定最大樣本量和Ⅰ類錯誤的條件下最大化檢驗效能

在固定樣本數量N時，通過選擇調整參數λ和γ，將Ⅰ類錯誤率控制在特定的預定水平下(例如10%)最大化檢驗效能。按以下步驟進行：

步驟1： 從臨床醫生得到H0和H1，從申辦方得到最大樣本量，從監管機構得到Ⅰ類錯誤率。

步驟2： 找到控制的Ⅰ類錯誤率以下的所有(λ,γ)值，可以通過數值網格搜索來執行。

步驟3： 在步驟2中確定的(λ,γ)集合中，選擇產生最大統計檢驗效能的集合作為最佳設計參數。

盡管BOP2設計是貝葉斯設計，但仍然必須確保設計具有所需的頻率學特性[29](例如Ⅰ類概率和檢驗效能)。可控制的Ⅰ類錯誤率，能彌補貝葉斯設計和頻率設計之間的鴻溝，使BOP2設計可供眾多用戶和監管機構使用。

1.3.2 控制Ⅰ類和Ⅱ類錯誤的條件下最小化期望樣本量

另一種優化策略是給定預定的Ⅰ類和Ⅱ類錯誤率，選擇λ和γ，在原假設為真的條件下，將樣本量N的期望值E(N|H0)最小化。Simon的二階段最優設計使用了這種優化標準。在這種方法中，不固定N，但是要優化設計參數，確定使E(N|H0)最小的(λ,γ,N)值，過程可以描述如下：

步驟1： 從臨床研究者得到H0和H1，選擇申辦方可接受的Ⅱ類錯誤率，從監管機構得到Ⅰ類錯誤率。

步驟2： 找到控制的Ⅰ類和Ⅱ類錯誤率以下的(N,λ,γ)值，可以通過數值網格搜索來執行。

步驟3： 在步驟2中確定的(N,λ,γ)集合中，選擇產生最小E(N|H0)的集合作為最佳設計參數。

在第2步中，有兩個約束條件(即Ⅰ類和Ⅱ類錯誤率)，但需要確定三個未知參數(N,λ,γ)的值。因此，原則上會得到無窮多個解。通過將N值限制在(Nmin,Nmax)范圍內可以解決此問題，其中Nmax是在實踐中可以提供的最大樣本量，由預算、增長率或其他實際因素決定。Nmin是試驗的最小樣本量，只要合理小(例如Nmin= 10)，就不會對設計的操作特性產生影響。給定N的特定值，基于兩個約束的網格搜索，可以唯一地確定λ和γ的值。此優化策略的一個潛在限制是無法直接控制樣本量N，并且在某些情況下，對于實際使用而言，使E(N|H0)最小的N值可能過大。因此，建議采用固定最大樣本量和Ⅰ類錯誤的條件下最大化檢驗效能的方法計算合理的樣本量。

2 實際案例分析

2.1 研究設計

根據文獻報道，一項注冊研究(NCT01210222)，試驗方案為每周靜脈注射15 mg·kg-1的特雷班尼布對持續或復發子宮內膜癌患者的療效[30]，與很多處于Ⅱ期的癌癥患者一樣，這些患者的特點是病情進展迅速，對新增化療藥不敏感。該試驗有兩個共同的主要療效終點：客觀緩解率和6個月無事件生存期。客觀緩解率使用RECIST 1.1[25]定義。無事件生存期(EFS)定義為從治療開始到首次發生任何事件的時間，包括疾病進展而無法進行手術治療、局部或遠處復發、任何原因導致的死亡等。這兩個終點都值得Ⅱ期研究中進一步探討，因為他們都有望成為總生存期(OS)的有效替代終點。

本研究的原假設H0的界值是根據基于相似人群的歷史數據集獲得，H0聯合規定ORR≤10%且EFS6≤20%，成立則認為治療無效。臨床上顯著差異是指6個月無事件生存期發生率增加20%，或客觀緩解率提高15%。所以，備擇假設EFS6≥40%或ORR≥25%，成立則認為該療法具有研發前景。

2.2 Web端軟件操作

操作界面友好，非統計專業人員也能熟練操作和理解，本節將演示2.1節的試驗案例軟件操作，用戶僅需選擇試驗主要終點的類型，中期觀察及最大樣本量，有效率或毒性率，Ⅰ類及Ⅱ類錯誤率等參數，即獲得試驗停止邊界的表格(結果見表3)，與Simon兩階段法設計類似，BOP2設計的一個重要的優點是試驗開始之前便可在試驗方案中列出停止邊界值，在試驗進行中，無需統計專業人員干預，研究者僅需計算出相關事件的數量，通過查表(表3)觀察是否超出邊界便可做出go/no-go決策。網站www.trialdesign.org免費開放，無需注冊。

表3 試驗案例NCT01210222的BOP2設計的停止邊界值Table 3 Stop boundary value of BOP2 design of trail case NCT01210222

2.3 研究結果

采用BOP2設計方法，在控制Ⅰ類錯誤率10%，已知最大樣本量55的條件下，對比文獻中兩階段法，本方法可中期觀察多次，以觀察4次舉例，結果見表3：入組28例患者中，至多2名患者獲得客觀緩解(CR或者PR)或者至多5名患者獲得6個月無事件生存期，則試驗終止，定論試驗藥物沒有研發前景；入組35例患者中，至多4名患者獲得客觀緩解(CR或者PR)或者至多7名患者獲得6個月無事件生存期，則試驗終止，定論試驗藥物沒有研發前景；入組48例患者中，至多6名患者獲得客觀緩解(CR或者PR)或者至多12名患者獲得6個月無事件生存期，則試驗終止，定論試驗藥物沒有研發前景；入組55例患者中，至多9名患者獲得客觀緩解(CR或者PR)或者至多15名患者獲得6個月無事件生存期，則試驗終止，定論試驗藥物沒有研發前景。考慮兩個終點正相關，該項研究檢測出臨床顯著效果的檢驗效能(把握度)是99.13%，顯著高于文獻中兩階段法的90%～92%的檢驗功效。

3 模擬研究

本節介紹原文中的模擬比較結果并給予充分解釋。BOP2作者通過模擬方法比較了BOP2與文獻中其他貝葉斯Ⅱ期設計，在模擬研究中，所有設計的Ⅰ類錯誤率控制在10%。下面將重點討論最大化檢驗效能的BOP2設計，最小化期望樣本量E(N|H0)可查閱文獻深入學習。在治療首個10例患者后進行了中期分析，以后每增加5例有結局患者后觀察一次，最大樣本量N=40。

在每個場景下模擬10 000次試驗，通過三個指標評估不同設計方法的性能：(1)拒絕無效假設(PRN)的百分比：定義為拒絕H0的模擬試驗的百分比。當H0為真時，PRN為Ⅰ類錯誤率；當H1為真時，PRN為統計檢驗效能。PRN也可以解釋為新療法有效的百分比；(2)提早終止概率(PET)的百分比：定義為提早終止的試驗的百分比；(3)實際樣本量：定義為10 000個模擬試驗中實際使用的平均樣本量。

3.1 二元療效終點

對于簡單的二元療效結局(即OR/無OR)，如試驗案例1構建了四對不同原假設H0和備擇假設H1的場景，并比較BOP2設計與Thall等提出的貝葉斯設計[8](簡稱為TS設計)，兩個設計主要的區別在于定義臨界值的方式不同(TS設計使用固定臨界值C，而BOP2設計使用適應性概率閾值C(n))。表2列舉出了BOP2設計的停止邊界值，以中期觀察到的有效的患者例數為依據，這些有效的患者用于在表4中場景1的每一次中期分析時做出go/no-go 決策。表4顯示了ORR的四對不同H0和H1的場景下，兩種設計的性能，分別列出4個場景下的PRN、PET和實際樣本量，模擬結果可得到BOP2設計產生的檢驗效能比TS設計大得多。例如，場景2中，原假設ORR為20%，備擇假設ORR為40%，當真實ORR為40%時，BOP2設計的檢驗效能為88.3%，而TS設計的檢驗效能僅為76.4%。此外，與TS設計相比，BOP2設計在新療法有效時錯誤地終止試驗的風險較小。例如，當真實ORR為40%時，TS設計錯誤地終止了23.5%的試驗，而BOP2設計錯誤地終止了11.4%的試驗。

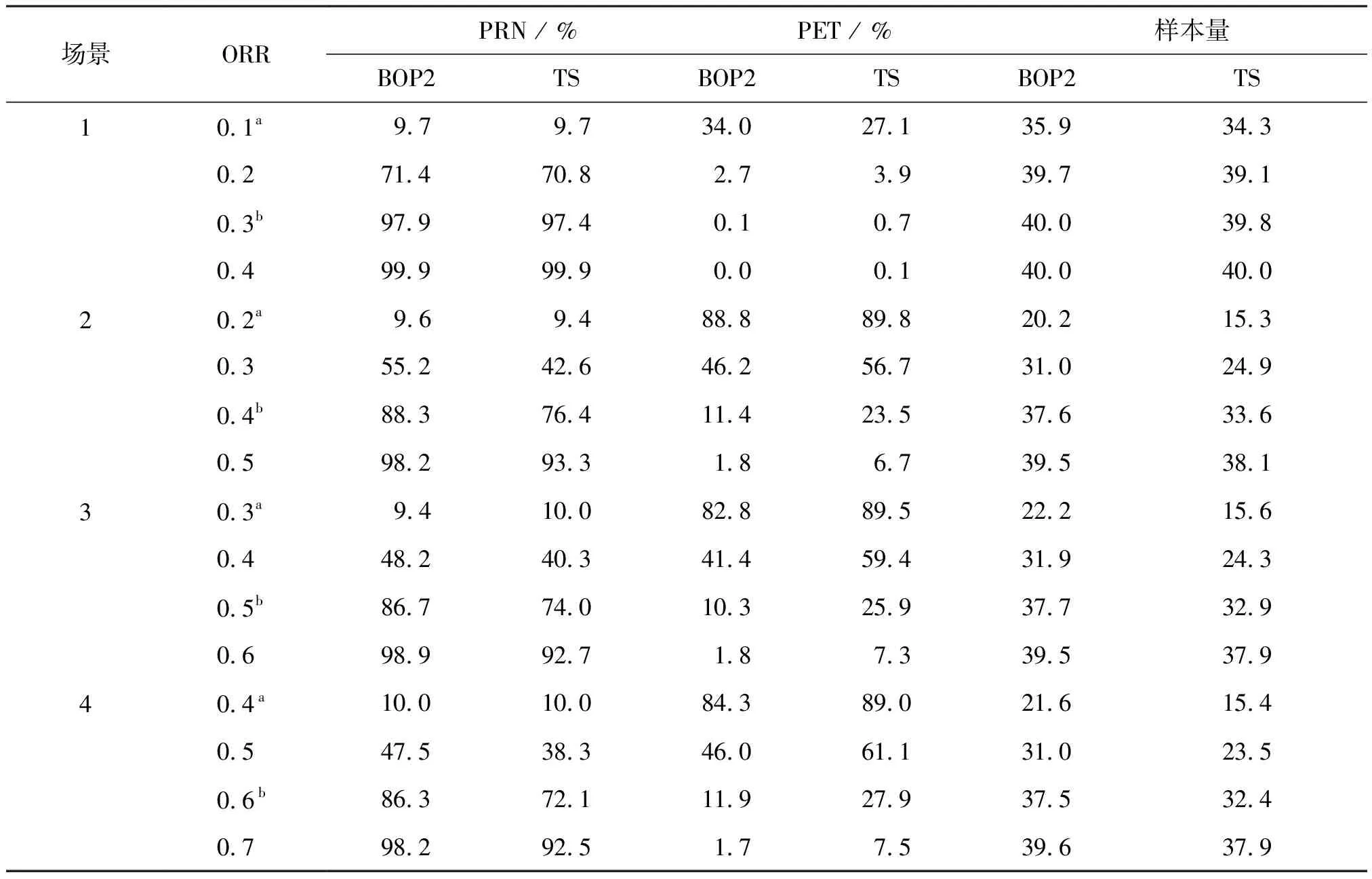
表4 試驗案例1二元療效終點中BOP2和TS設計PRN、PET及實際樣本量模擬結果比較Table 4 Comparison of BOP2 and TS design PRN, PET and actual sample size simulation results in the binary efficacy endpoint of trail case 1

在原假設下，TS設計比BOP2設計更有可能終止試驗。因為TS設計有終止試驗的高趨勢，所以它的實際樣本量比BOP2設計小。由于觀察到的數據具有離散性，并且定義臨界值的方式不同，在某些場景下，不可能將兩種設計的Ⅰ類錯誤率精確匹配到10%。這就解釋了在場景1中，TS設計的Ⅰ類錯誤與BOP2設計相等，而在場景2中，則略高。

3.2 嵌套的療效終點

表5顯示了在試驗案例2的嵌套療效終點的模擬結果，表2給出了相應的停止邊界值。最初的10名患者入組后開始中期觀察，然后每5名患者入組后進行中期監測。情景1是原假設，即H0:Pr(CR)≤0.15和Pr(CR+PR)≤0.3，情景7是備擇假設，即H1:Pr(CR)≥0.25或Pr(CR+PR)≥0.5。同樣將BOP2設計與TS設計進行比較，如表5所示，BOP2設計通常比TS設計具有更大的檢驗效能。如在場景7中，Pr(CR)=0.25,Pr(CR+PR)=0.5，則BOP2設計的檢驗效能為85.5%，而TS設計的檢驗效能僅為74.2%。比較這兩種情況，觀察到當真實的CR率從15%增加到20%時，BOP2設計可以將PRN從8.7%增加到24.2%。這恰好滿足了可以對BOP2設計的期望，該設計可以同時監測嵌套的終點。相反，TS設計無法區分這兩種情況，因為CR+PR比率均為30%。另外，當治療實際上有效時，TS設計比BOP2設計傾向于更大的概率錯誤終止試驗。如在場景7中，TS設計提前25.7%的時間終止了試驗，而BOP2設計提前了9.9%的時間終止了試驗。同樣，由于早期終止試驗的可能性很高，TS設計的實際樣本量小于BOP2設計的樣本量。

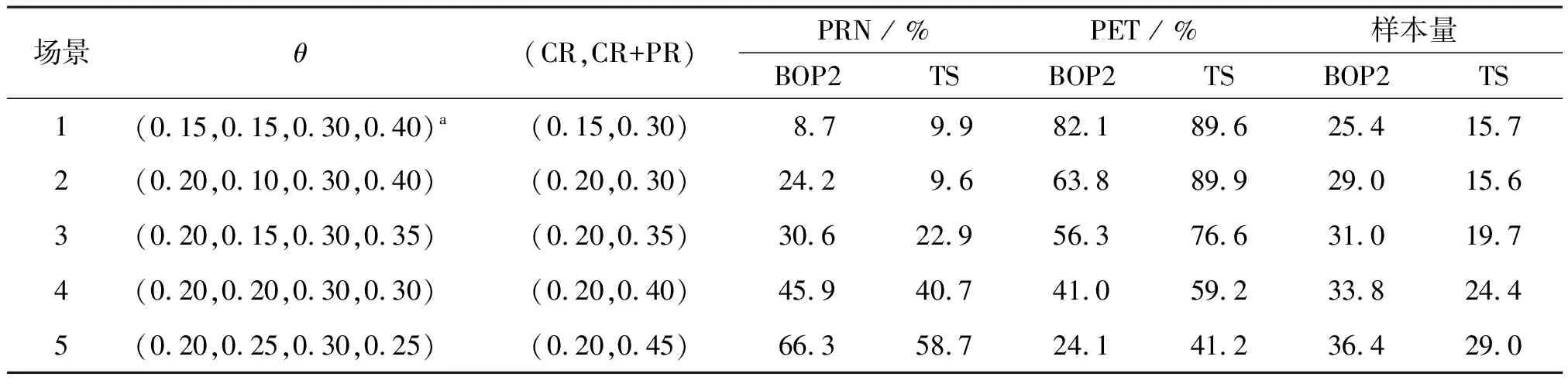
表5 試驗案例2嵌套的療效終點中BOP2和TS設計PRN、PET及實際樣本量模擬結果比較Table 5 Comparison of BOP2 and TS design PRN, PET and actual sample size simulation results in the nested efficacy endpoint of trail case 2

續表

場景θ(CR,CR+PR)PRN / %PET / %樣本量BOP2TSBOP2TSBOP2TS6(0.25,0.20,0.30,0.25)(0.25,0.45)72.359.019.340.937.129.17(0.25,0.25,0.25,0.25)b(0.25,0.50)85.574.29.925.738.533.08(0.30,0.25,0.25,0.20)(0.30,0.55)95.785.23.014.839.535.9

3.3 共同主要療效終點

表6顯示了在試驗案例3具有兩個共同主要療效終點(即ORR和PFS6)的模擬結果，表2列出了相應的停止邊界值。場景1和7分別展示了H0和H1。將BOP2設計與Thall等[18]提出的貝葉斯設計進行了比較，并將后者簡稱為TSE設計。為了公平比較，TSE設計與BOP2設計使用的模型和停止規則相同，只是臨界值的方式不同(TSE設計使用固定臨界值C，而BOP2設計使用適應性概率閾值C(n))。結果與前述案例一致，與TSE設計相比，BOP2設計產生了更高的統計檢驗效能，和更低的錯誤終止試驗的概率。

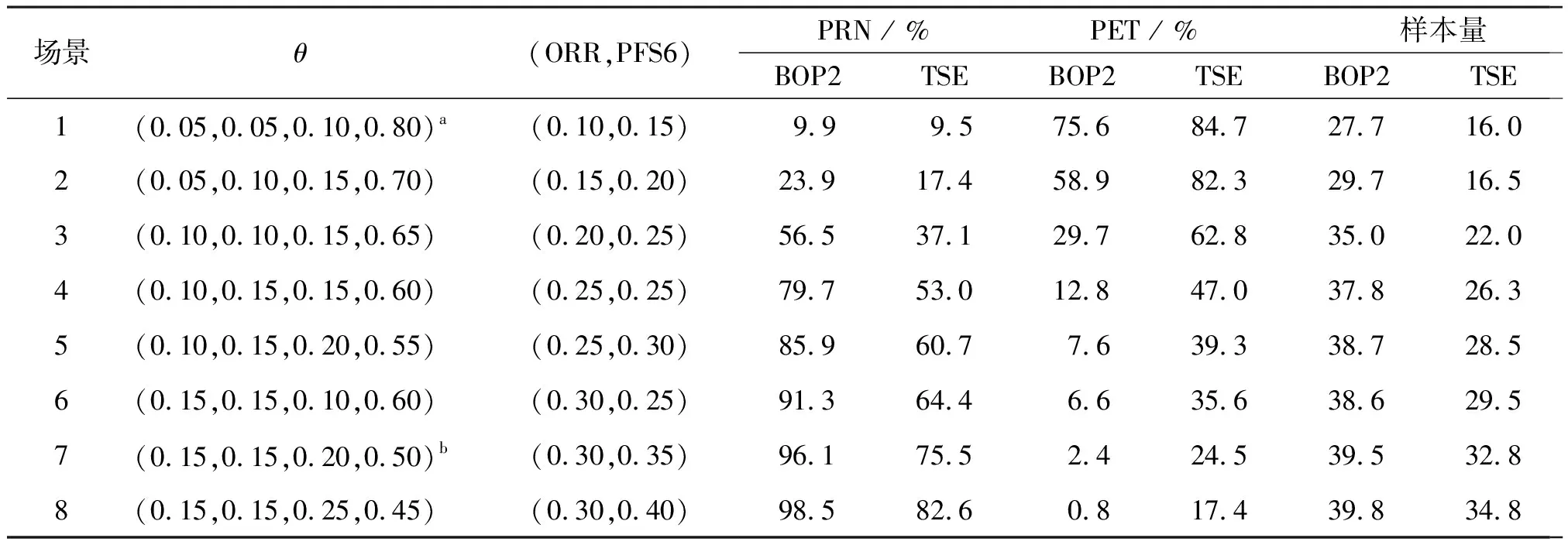
表6 試驗案例3共同的主要療效終點中BOP2和TSE設計PRN、PET及實際樣本量模擬結果比較Table 6 Comparison of BOP2 and TSE design PRN, PET and actual sample size simulation results in the common primary efficacy endpoint of trial case 3

3.4 聯合監測療效和毒性終點

表7顯示了在試驗案例4的模擬結果，該案例同時監控療效和毒性。場景1和7分別代表H0和H1。同樣對BOP2設計與TSE設計進行了比較，TSE設計與BOP2設計使用相同的模型和停止規則，只是TSE設計在停止規則中使用了固定的臨界值C。同樣，在相同的Ⅰ類錯誤率(即場景1中的PRN)的情況下，BOP2設計的性能優于TSE設計，具有更高的檢驗效能，并且錯誤終止試驗的風險較小。

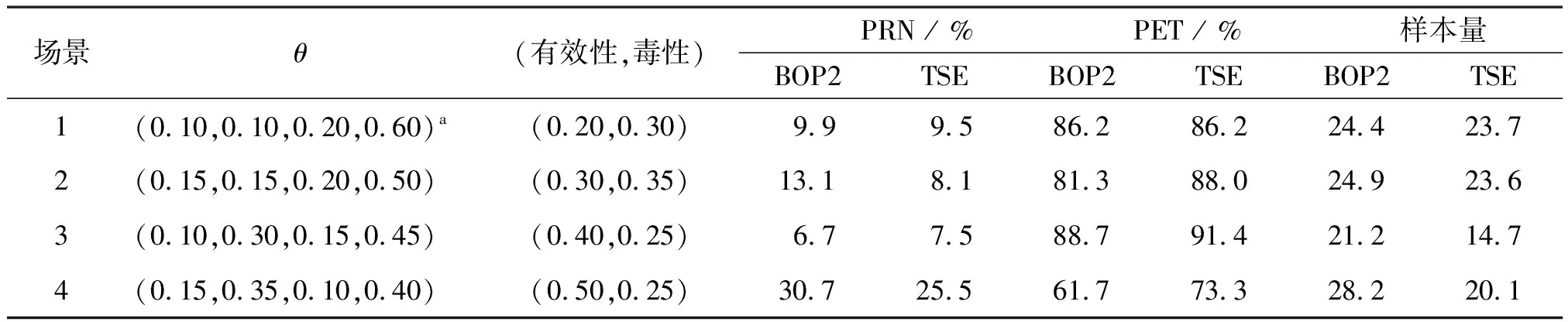
表7 試驗案例4聯合毒性和有效性療效終點中BOP2和TSE設計PRN、PET及實際樣本量模擬結果比較Table 7 Comparison of BOP2 and TSE design PRN, PET and actual sample size simulation results in the combined toxicity and effectiveness efficacy endpoint of trial case 4

相應的停止邊界在表2中列出。在這種情況下，停止邊界的使用與以前的案例略有不同。例如，在治療30位患者之后，如果CR次數≤5或毒性反應≥10，則BOP2設計將終止試驗。

續表

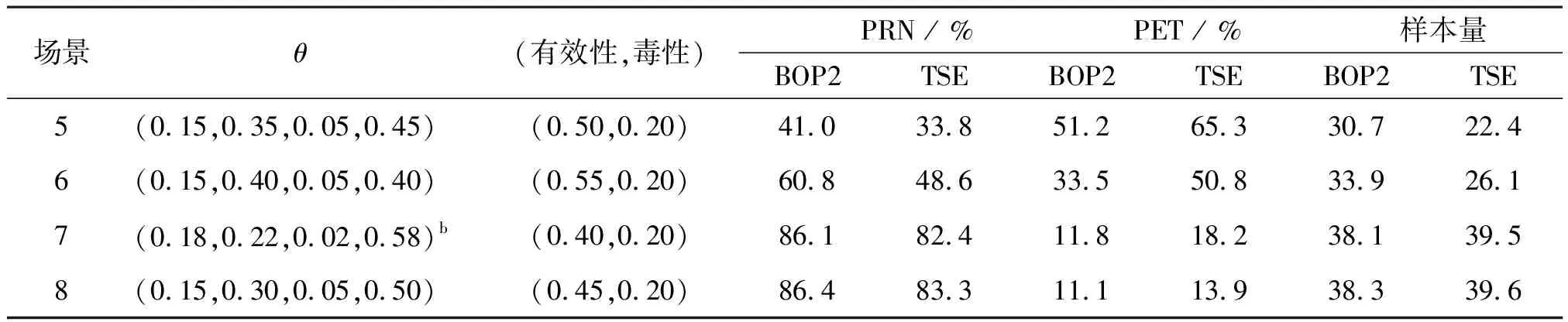
場景θ(有效性,毒性) PRN / % PET / % 樣本量BOP2TSEBOP2TSEBOP2TSE5(0.15,0.35,0.05,0.45)(0.50,0.20)41.033.851.265.330.722.46(0.15,0.40,0.05,0.40)(0.55,0.20)60.848.633.550.833.926.17(0.18,0.22,0.02,0.58)b(0.40,0.20)86.182.411.818.238.139.58(0.15,0.30,0.05,0.50)(0.45,0.20)86.483.311.113.938.339.6

4 結 論

隨著Ⅰ期臨床試驗完成對試驗藥物的安全性和耐受性的初步評估，新藥研發會進入Ⅱ期臨床試驗階段。Ⅱ期主要目的是評估藥物在推薦劑量下的治療效果，并進一步監控藥物的毒性，防止過多的患者暴露在可能無效的治療中。其中Ⅱa期臨床試驗的基本特征是早期無效終止和中期go/no-go決策，只有新療法在Ⅱ期試驗階段表現出足夠強的有效性，研發才會進入到耗時更長、耗資巨大的Ⅲ期臨床試驗。

目前國內的Ⅰ期臨床試驗已不再局限于傳統的3+3設計，基于區間的BOIN、Keyboard和基于模型的CRM等貝葉斯適應性設計方法也被統計專業人員、研究者所接受、掌握和應用。著眼于Ⅱa期試驗高效的設計方法，本文討論的BOP2設計是一種靈活的貝葉斯優化設計，該設計能夠同時處理簡單(例如二元)和復雜(例如有序，嵌套和共同多)終點。設計使用Dirichlet-多項式模型統一適應不同類型的終點。且與Simon兩階段相比，BOP2設計可以多次中期觀察，在每個中期階段，通過評估事件的后驗概率來做出go/no-go決策，在原假設下，對該決策概率進行優化，以最大程度地提高檢驗效能或減少患者人數。模擬研究表明，較其他現存的貝葉斯Ⅱ期設計，BOP2設計精確控制Ⅰ類錯誤率，保證患者風險最小化，具有更高的檢驗效能及更低錯誤地終止試驗的風險，彌補了貝葉斯設計和頻率設計之間的差距。此外，BOP2設計可以在試驗設計階段便枚舉出終止邊界值。這些特性使得BOP2設計可供眾多用戶和監管機構使用，且易于實現。

這一高精度、對試驗過程高安全保障、對患者受益最大化的方法將推動中國早期臨床試驗的高速發展，雖然中國的新藥臨床試驗日漸擺脫程式化，逐漸與國際接軌，總體研發能力和監管水平有了極大水平的提高，但是，早期新藥臨床試驗因其特殊性和復雜性，無論是方案設計、試驗管理以及最后的總結分析，仍然有非常大的提升空間，急需更多的研究人員發掘高效、高精度、高質量的方法，并應用在實踐當中。