湍流燃燒機理和調控的活性子空間分析方法
王娜娜,解青,蘇星宇,任祝寅,,*
1.清華大學 航空發動機研究院,北京 100084 2.清華大學 燃燒能源中心,北京 100084
湍流燃燒是航空發動機、沖壓發動機、組合發動機、內燃機等動力裝置工作的核心能量轉換過程,燃燒組織的好壞直接關系到發動機的壽命、效率、污染物排放等[1-2]。而發動機湍流燃燒過程十分復雜,包括湍流、霧化/蒸發、輻射等多物理過程以及和化學反應的強耦合,具有非定常、多尺度的特征。目前隨著更嚴格的高效、低排放等要求[3],湍流燃燒開始趨于近極限燃燒組織[4-5],亟需在穩定可控燃燒方面取得突破。這就需要進一步加深對湍流燃燒機理的認識,實現流動和化學反應的有效匹配和調控。對于該問題,數值仿真是當前重要的研究手段之一[6-7],從而支撐航空發動機的自主研發,仿真技術體現了一個國家的高端裝備研發水平[8]。
然而,數值模擬中的湍流模型、燃燒模型和化學反應動力學模型等均涉及大量模型參數,這些參數可能具有很大的不確定性。以化學反應動力學為例,從氫氣到大分子碳氫燃料的反應機理由數十到近千步反應組成,而每步反應均有一定的不確定性,導致僅在化學反應動力學模型中,就存在海量的不確定性參數[9-11]。這些模型參數的不確定性將導致仿真結果存在不確定性[12]。隨計算機技術的發展、數值模擬研究方法重要性的提升,湍流燃燒模擬的不確定性分析在國內國際上得到了越來越多的關注[13]。2014年,美國NASA經過大量調研形成了一份綜合分析報告[14],對計算流體動力學(Computational Fluid Dynamics, CFD)所涉及的技術到2030年時的需求及能力做了分析和預測。其中,針對不確定性分析單獨給出了發展時間軸,預測在2025年之前需要實現不確定性在CFD中的傳遞。湍流燃燒模擬的模型不確定性來自于模型假設自身的不確定性以及模型參數的不確定性,前者可稱為模型格式不確定性,Mueller和Raman[15]在這方面開展了大量工作,探究了小火焰燃燒模型不確定性在湍流燃燒模擬中的傳遞。本文則主要綜述包含模型參數在內的輸入參數不確定性在湍流燃燒中的傳遞。輸入參數的不確定性分析可以得到各部分模型參數以及初始/邊界條件不確定性的傳遞規律和參數敏感性,揭示湍流燃燒的主控物理機制,有助于量化數值仿真精度,提高航空發動機的設計和優化水平,尤其對近極限條件下如高溫升航空發動機、超聲速沖壓發動機的設計具有重要意義。
湍流燃燒的輸入參數空間通常包含化學反應動力學模型的反應常數、湍流模型、燃燒模型參數以及初始/邊界條件。由于參數眾多且單次多維湍流燃燒模擬計算成本高,使得湍流燃燒模擬的不確定性和敏感性分析面臨的最大困難是“維度災難”。因此,目前已有的研究集中在單一模型和少量模型參數的不確定性分析上。在化學反應動力學模型不確定性研究方面:學者利用靈敏度分析法降維,研究了化學反應速率常數不確定性對模型預測輸出[16]、火焰傳播速度[17]的影響,聲振對層流預混火焰的火焰傳遞方程的影響[18],以及輸運概率密度函數法湍流火焰模擬中單一基元反應對射流抬舉高度和局部熄火/再燃的影響[19-22]。在湍流模型不確定性研究方面:學者基于多項式混沌展開,研究了Smagorinsky模型系數Cs和湍流普朗特數以及施密特數不確定性在非預混鈍體穩定火焰大渦模擬(Large Eddy Simulation, LES)中的傳遞[13],Cs不確定性對湍動能預測影響[23],雷諾平均法(Reynolds-Averaged Navier Stokes, RANS)單方程和雙方程模型系數層面的不確定性分析[24],模型系數對不同雷諾數下管道流動的影響[25],基于重心圖法的模型格式層面的不確定性分析[26-27],以及在高速射流[28]、邊界層分離[29]等問題中的應用。在燃燒模型不確定性研究方面:學者研究了小火焰模型不確定性在Sandia D火焰LES中的傳遞[30],進一步,采用隨機搭配法研究了Delft III射流火焰上游溫度不確定性對下游碳煙生成預測的影響[31],以及湍流燃燒模型格式不確定性對混合分數、溫度分布以及一氧化碳生成的影響[15]。
然而僅考慮單一模型的不確定性無法量化多物理耦合下不確定性傳遞規律、難以表征不同物理過程中的主控因素。同時將化學動力學模型、湍流模型、燃燒模型以及初始/邊界條件納入不確定性研究中,可以從全局敏感性的角度分析輸入參數對湍流燃燒目標量影響的內在物理機制,是當前一個重要研究方向。開展考慮多模型和初始/邊界條件的湍流燃燒不確定性研究的關鍵是有效的海量輸入參數降維方法。
近幾年,Constantine等[32-33]提出了活性子空間(Active Subspace, AS)降維方法,該方法基于梯度的偏協方差矩陣特征分解,得到活躍特征方向,構建輸入參數低維子空間,利用輸入參數在該子空間的投影得到活躍變量,降低輸入參數維度。該方法和其他常用敏感性降維方法的區別在于,敏感性分析保留的是影響較大的輸入參數,而子空間分析保留的是影響較大的輸入參數空間中的方向,這些方向是參數自身的線性組合,從而實現最大程度降維的同時保證精度。同時,活躍方向向量的分量值提供了目標量相對于輸入參數的全局敏感性信息[34]。AS方法和其他常用降維方法如主成分分析(Principle Component Analysis, PCA)法均是對空間進行基的變換,識別重要方向,以達到降維的目的。但是兩者仍有本質區別:前者得到的重要方向上映射的梯度最大,而后者分析中,沿重要方向數據的方差最大。也就是說AS分析對象為高維映射,而PCA分析對象為數據集;前者可得到低維響應面或預測模型,后者的目的則是實現對物理系統的低維描述。在燃燒領域的研究中,PCA被廣泛用來識別化學反應系統的低維流形[35]、重構組分空間[36]以降低反應系統維度,并在后續燃燒問題求解中只對少數個主成分(Principle Components, PCs)求解輸運方程[37-40],可極大地減少LES等湍流燃燒模擬中組分方程的個數[41-43]。
目前活性子空間方法在動力裝置的機理分析和優化方面已有了成功應用。Constantine等[44]采用活性子空間方法將七維運轉參數降為一維,研究了它們對HyShot II沖壓發動機性能的影響。最近,Constantine等進一步將活性子空間方法應用在了設計方法發展[45]、翼型設計[46]、渦輪葉片設計[47]、以及高超聲速模擬不確定性分析[48]中。Magri等[49]采用該方法分析了雙環形燃燒器的熱聲穩定的不確定性,Guan等利用活性子空間構造了碳氫燃料辛烷值[50]和標準生成焓[51]的預測模型,并且將該方法應用在了可變正時汽油機的換氣策略標定中[52]。
在湍流燃燒控制機理和模擬不確定性量化方面,Ji等首次將該方法應用在了化學反應動力學模型不確定性在自著火、層流火焰[53]和湍流火焰[54]模擬中的傳遞研究中,他們在零維燃燒模擬和湍流燃燒模擬中均得到了反應速率常數的低維子空間。Vohra等[55]將速率常數、活化能以及初始狀態均考慮到輸入參數空間中,對H2/O2反應得到了一維子空間。這些研究都實現了對海量化學動力學模型參數的降維。Wang等則率先發展了反應動力學、物理模型和邊界條件參數連續降維方法,將動力學模型參數降維得到一維活性子空間后,聯立湍流燃燒模型參數和邊界條件參數再一次降維[56],得到了物理化學模型參數和邊界條件不確定性的傳遞規律,揭示了超聲速湍流射流火焰的主控物理機制[57]。活性子空間方法在湍流燃燒模擬的不確定性量化和主控機制分析方面有巨大的應用潛力,并且有助于后續的湍流燃燒調控分析。
本文將綜述活性子空間方法在湍流燃燒模擬中已有的應用。首先簡述活性子空間方法理論及針對湍流燃燒模擬發展的連續降維方法。然后介紹動力學參數、物理模型參數以及邊界條件不確定性在燃燒模擬中傳遞的典型應用,以及研究得到的湍流燃燒機理。并進一步討論展望基于活性子空間分析方法的湍流燃燒調控。
1 活性子空間方法
活性子空間方法可以在m維輸入參數空間x∈m中識別出對應于目標量(Quantity of Interest, QoI)即輸出量f(x)的低維結構,沿該低維方向f對x的梯度最大。通過對f(x)梯度的協方差矩陣做特征分解,可以得到輸入空間的活性子空間:
(1)
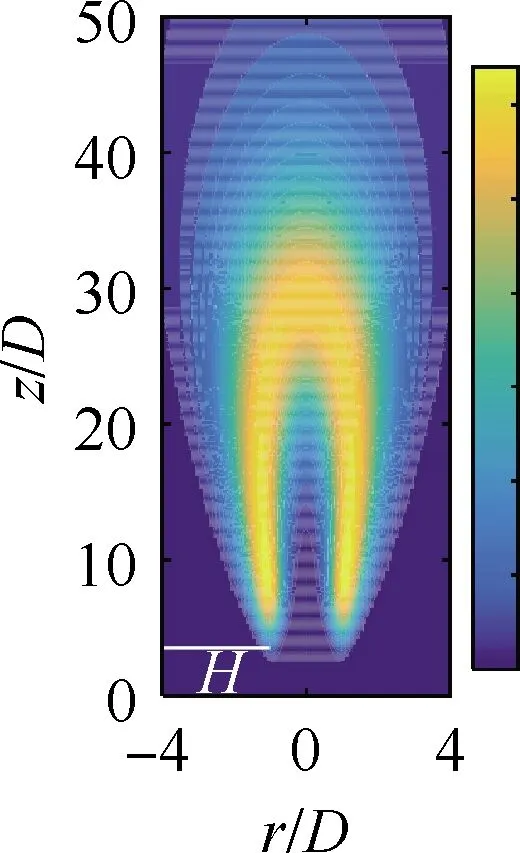
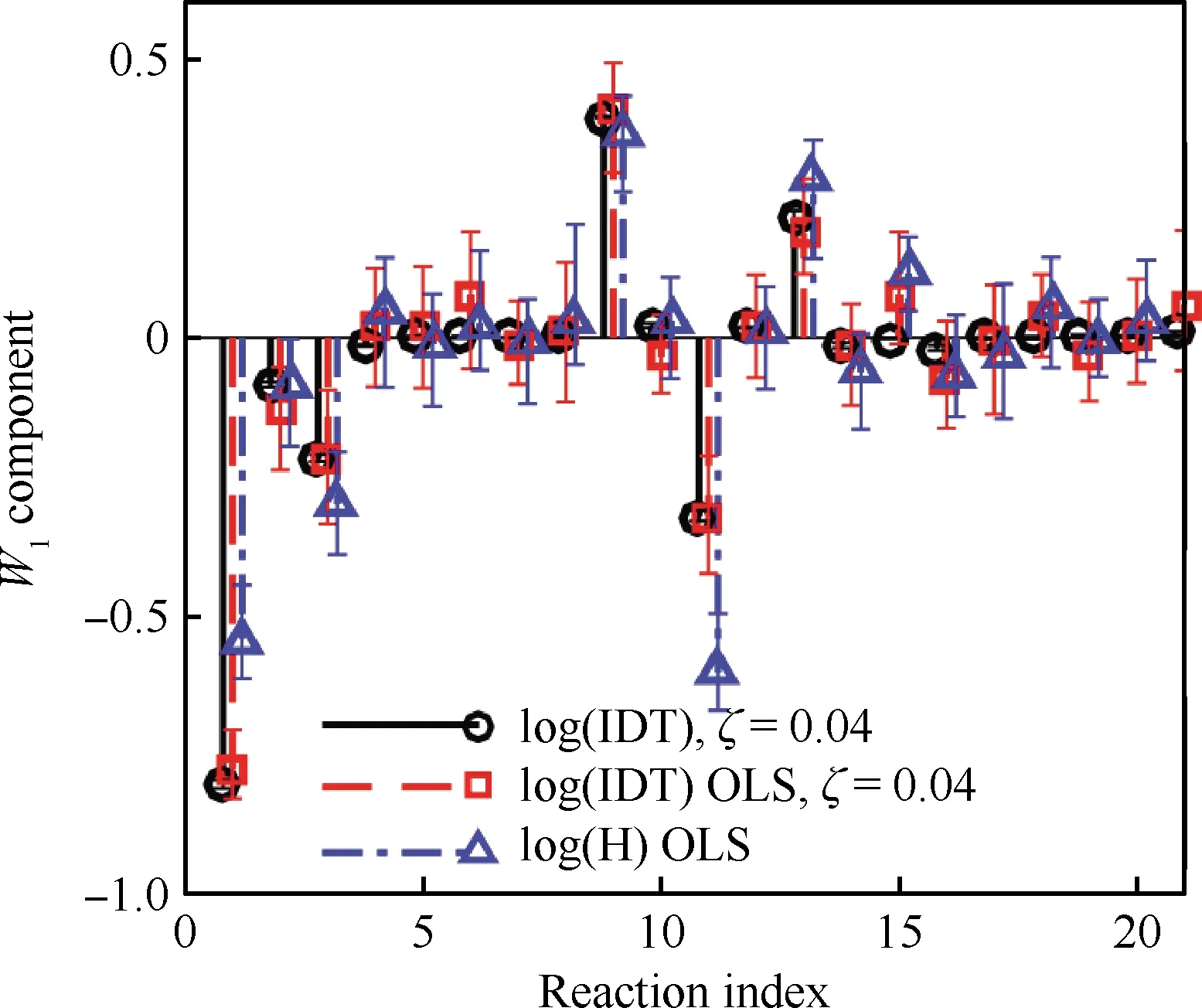
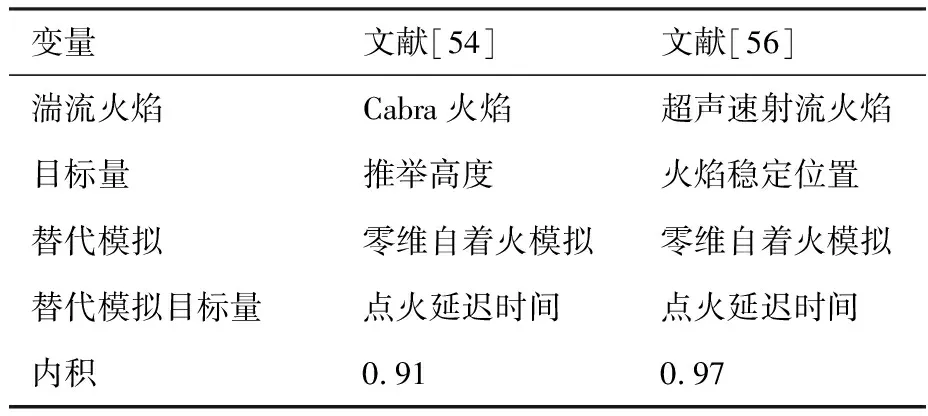
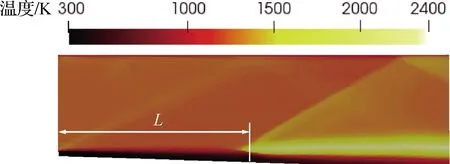
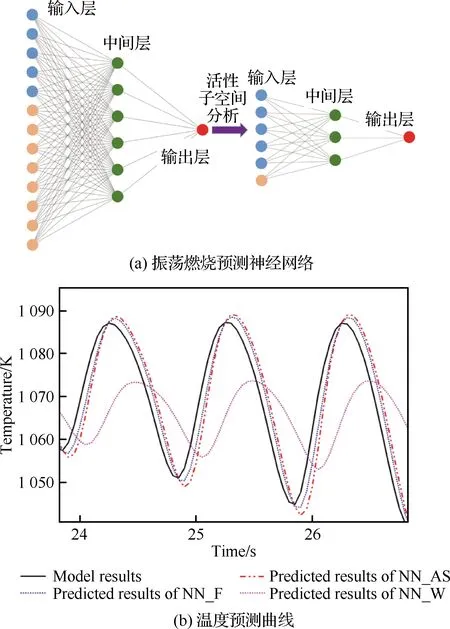
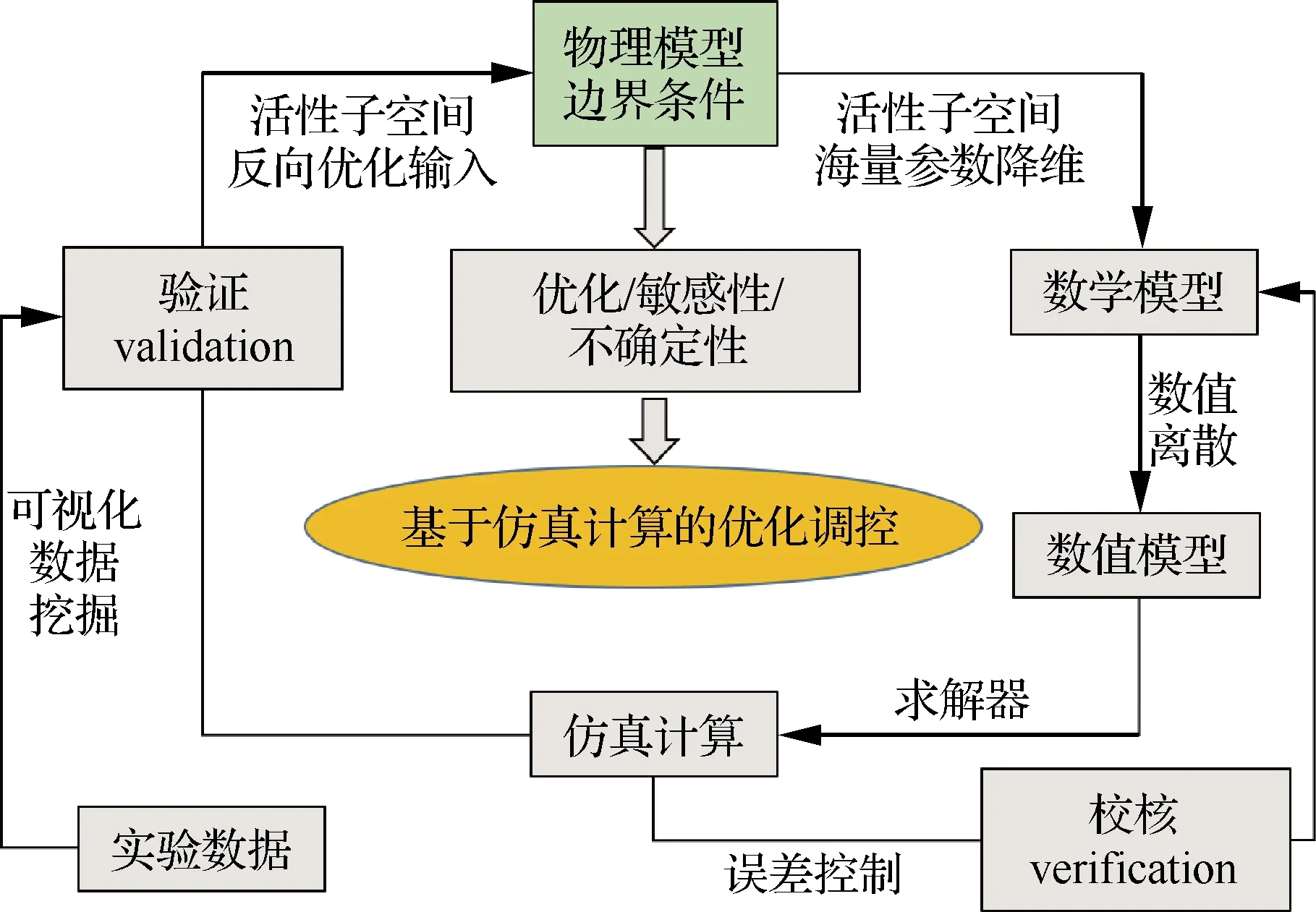
式中:π為輸入參數的聯合概率密度函數(Probability Density Function, PDF);C為對稱半正定矩陣;W=[w1,w2,…,wm]為特征向量矩陣;Λ=diag(λ1,λ2,…,λm)為對應特征值組成的對角矩陣;其中λ1,λ2,…,λm從大到小降次排列,如果特征值λn遠大于λn+1,即λn?λn+1,n 圖1 活性子空間分析中基變換以及響應面構建示意圖 如果在仿真計算中可以直接得到映射f的梯度,那么,活性子空間可通過如下步驟在輸入空間中的隨機采樣計算得到: 1)根據輸入參數x∈m的概率密度分布π(x),在輸入空間采M個樣本{x(1),x(2),…,x(M)}。 3)估算矩陣C: 5)根據特征值的大小將特征值矩陣和特征向量矩陣分塊: (2) (3) 接著對C進行特征分解,進行后續活性子空間分析。目前有限差分、全局線性擬合以及全局二次擬合均在實際中有了成功應用,表1總結了3種方法需要的樣本數以及應用的文獻[59-60],其中,α為取樣系數,β為期望獲得的子空間最大維度。 表1 梯度近似方法 以上討論的為針對單一目標量的活性子空間,對于多目標量,Ji等[53]發展了共享活性子空間方法。假設對于d個目標量,映射fi可以完全降維到其一維活躍向量ui所展成的一維活性子空間中(i=1,2,…,d),即 (4) (5) 若對于i=1,2,…,d式(5)均成立,則v即為d個目標量的共享子空間。經過對v的求解發現,共享子空間是單一目標量子空間的線性組合。對于實際燃燒問題,由于物理過程的復雜性,在構建多目標量的共享子空間時,可增加每個單一目標量的活性子空間維度,以囊括更多的物理過程,提高共享子空間中對原空間映射近似的準確性。詳細推導以及高維活性子空間的共享子空間方法可參見Ji等[53]文獻。獲得共享子空間后,在對多目標量的不確定性PDF量化和多目標量優化調控時,可以極大增加計算效率。對于多目標量優化,由于AS識別的是梯度變化最大的方向,并以該方向為基構建子空間,因此即使目標間存在矛盾性關系也不影響共享子空間的建立,但會體現在不同目標量在該子空間中響應面不同上。在進行后續的多目標優化調控時,則需根據實際問題需求,進一步建立代價函數,通過極小化代價函數,對輸入參數進行折中調控,達到多目標量優化的目的。 對于帶有詳細化學反應的湍流燃燒模擬,不確定性來自于模擬反應動力學的反應機理以及燃燒模型、湍流模型等物理模型和初始/邊界條件。通常碳氫燃料的反應機理包含數十到數千個基元反應,考慮每個基元反應建模參數的不確定性,輸入參數空間將達到數十到數千維。此時,即使采用活性子空間方法,所需的樣本數即湍流燃燒模擬次數仍然巨大,在當前的計算資源下難以實現。因此,Wang等提出連續降維方法[56],如圖2所示,利用零維或一維化學動力學模型作為替代模型,首先將動力學模型參數進行降維,降維后的活性動力學參數與物理模型參數組成新的輸入空間再次降維,實現采用較小計算量完成湍流燃燒仿真不確定性分析和主控物理機制分析。以下對該方法進行簡單闡述。 圖2 連續降維方法示意圖 第1步為反應動力學參數空間降維。首先,根據實際工況的湍流燃燒模擬提取出用于零維或一維替代模型模擬的初始條件,選取適當QoI替代湍流燃燒模擬中的真實QoI。此處,適當QoI對子空間分析的合理性將在3.1節中通過文獻結論綜述進一步說明。再次,利用子空間分析得到替代模型映射的活躍方向。最后,將原輸入參數向量投影到活躍方向上,得到對應活躍變量,對于碳氫燃料來說,活躍變量的個數通常為1~5個[53],從而實現由數千維到個數維的動力學參數降維。 第2步為動力學和其他物理模型參數空間降維。首先,將第1步中得到的活躍變量與物理參數組成新的輸入空間,此時該空間維度由于第1步的降維已較原輸入空間有了極大程度的降低。再次,在降維空間中采少量樣本進行湍流燃燒模擬,進行活性子空間分析,得到該降維空間的活性子空間。最后,在該子空間中構建低維響應面,進行不確定性量化計算,同時根據子空間分析目標量的主控物理機制。 對于復雜的燃燒問題,如燃氣輪機燃燒室中的燃燒過程,在明確目標量的基礎上,選擇和目標量所涉及的主要物理過程一致的零維或一維模擬,作為替代模擬。在復雜燃燒過程的熱力學狀態時空演化中選取若干狀態點作為替代模型的初始狀態,分別求解不同狀態下的活性子空間。最后結合共享子空間方法,得到上述子空間的共享子空間,以及對應的動力學活躍變量,用于后續動力學-物理模型參數降維。 本節首先綜述了化學動力學參數不確定性的活性子空間分析;接著,綜述了輸入參數拓展到物理模型常數和邊界條件的情況,并且簡明闡述了文獻中分析得到的湍流燃燒機理。另外,綜述了活性子空間方法在模型燃燒系統的性能預測中的應用。最后,討論了基于活性子空間分析方法的湍流燃燒調控。 Ji等[54]針對湍流射流Cabra火焰[61]開展了活性子空間分析,研究了動力學參數的不確定性在湍流燃燒模擬中的傳遞。射流火焰的模擬結果如圖3所示,目標量為火焰推舉高度H。在他們的工作中,采用了氫氣/空氣反應機理Li-2004[62]機理以模擬氫氣氧化的反應動力學過程。將基元反應的速率常數作為不確定性輸入參數,進一步依據Sheen等[63]的研究將速率常數定量為相互獨立的對數正態分布: 圖3 Cabra湍流射流火焰OH質量分數云圖仿真結果[54] (6) 式中:kr為第r個基元反應的速率常數;kr0為其對應的名義值;Fr為其對應的不確定性因子[64],各個反應所對應的Fr見表2。 表2 基元反應所對應的不確定性因子 通過分析84個湍流燃燒模擬樣本數據,得到了21維動力學參數空間的活性子空間,對應活躍方向的分量如圖4中三角符號所示。由該分量得到的全局敏感性信息可以看出,鏈分支反應R1和R11對火焰推舉高度的影響最為顯著,其次,反應R9的影響也較為顯著,但是其分量符號與R1和R11相反,原因是該反應降低了混合氣的活性從而抑制了自著火的發生。之后,他們在該一維子空間中利用多項式擬合構建了一維響應面,最后通過50 000個樣本點得到了火焰推舉高度的不確定性概率密度分布。 此外,Ji等在他們的工作中探究了采用零維自著火模擬計算子空間,該模擬的工況為Cabra射流火焰模擬的參考工況,目標量為點火延遲時間(Ignition Delay Time, IDT)。得到的動力學參數的活性子空間如圖4中的圓圈符號和正方形符號所示,兩者分別為采用有限差分和全局線性擬合得到的結果。通過對比采用湍流燃燒模擬和零維自著火模擬得到的活躍向量方向,Ji等認為,實際湍流燃燒中擴散作用使得火焰穩定區域前緣的HO2濃度較高,而零維自著火模擬中不能體現擴散作用,所以R11和R13在零維模擬的影響小于其在湍流燃燒模擬中的影響。但總體來說,兩者最敏感的基元反應均是R1、R9和R11,并且,兩者的活躍方向向量的內積為0.91,說明方向幾乎一致。 圖4 Cabra火焰推舉高度的活躍方向分量[54] 因此,Ji等認為,如果低成本替代模擬和湍流燃燒模擬的主控物理過程一致,那么,可以采用替代模型初步探究子空間的維度以及活躍方向向量的主控分量,從而確定敏感度較大的輸入參數。進一步,可以在湍流燃燒模擬中將不敏感的輸入參數剔除,從而減少樣本個數,減少活性子空間分析的計算成本[54]。Wang等[56]同樣開展了替代模型和對應湍流燃燒模擬的活性子空間分析,通過兩者得到的活躍方向向量的內積為0.97,表3總結了文獻中采用替代模型和湍流燃燒模擬得到的子空間的相近程度。該結果進一步說明對于湍流燃燒模擬中動力學參數部分,可以采用具有相同主控物理過程的低成本替代模擬進行確定,從而降低湍流燃燒模擬的樣本數和計算成本,同時也說明了第2節中所闡述的連續降維方法的合理性。 表3 替代模擬和湍流燃燒模擬活躍方向內積 Wang等[56-57]采用連續降維方法分析了Burrows-Kurkov(B-K)超聲速壁面射流火焰[65-66]的主控物理機制。火焰的溫度云圖如圖5所示,其中L為火焰推舉長度。圖6展示了火焰推舉長度對輸入參數的敏感性,作者發現,動力學參數中反應R1、R3以及R9對火焰的點火起始位置影響最為顯著,如圓圈符號所示,其中反應標號和表2中給出的一致。反應R1主導了火焰點火位置,這與Wu等[67]對B-K火焰的化學爆炸反應模態分析的結論一致,即他們研究發現,火焰穩定位置上游處的OH和H主導了化學爆炸混合層。 圖5 B-K火焰溫度云圖仿真結果[56] 圖6 B-K火焰推舉長度的活躍方向向量分量[56] 當進一步將湍流模型和燃燒模型參數考慮在內時,此時的活躍方向分量展示了推舉長度對動力學和物理模型參數的敏感性,以及物理模型參數的攝動動對關鍵反應的影響,如圖6中三角符號所示。可以看出反應R1和湍流普朗特數(Prt)對推舉長度的影響最顯著,根據該子空間中響應面的單調遞增[56]特性,可以進一步得出,R1的反應速率越快或湍流普朗特數越大則推舉長度越小,這是因為R1反應速率的增加可以減短自著火時間,湍流普朗特數的增加則會減小當地的湍流熱擴散,兩者都將有利于氫氣自著火的發生,從而使得推舉長度減短。另外作者從輸入空間參數攝動相互影響的角度得出,當物理模型的參數為不確定性輸入參數時,動力學模型參數中H2/O2鏈分支反應的敏感性被略微抑制,而HO2生成和消耗反應的敏感性被一定程度增強,從而揭示了B-K火焰點火起始位置的主控過程以及他們之間的相互作用機制。 圖7 活性子空間隨壁面射流火焰流向的空間演化[57] Ji等[53]發展了基于活性子空間的共享子空間方法,用來解決多目標量的活性子空間問題。他們用該方法探究了內燃機甲烷和二甲醚(DME)均質壓縮點火(Homogeneous Charge Compression Ignition, HCCI)的點火曲軸轉角和點火失敗概率。在該研究中,采用零維HCCI模型模擬的燃燒系統來近似三維湍流燃燒模擬。HCCI的子空間由點火過程中6個熱力學狀態下的定容自著火模擬訓練得到,其中對于DME,該6個熱力學狀態包含了由低溫化學帶來的兩級著火和負溫度系數(Negative Temperature Coefficient, NTC)的狀態點。以下簡要闡述DME點火過程主控物理機制的活性子空間分析。 圖8(a)展示了低溫(650 K)、中等溫度(850 K)以及高溫(950 K)HCCI點火過程中參考狀態下的點火延遲時間的第1個活躍方向向量分量。其中低溫工況包含了兩級著火,高溫工況為一級著火過程。可以看出,不同溫度下IDT的活躍方向具有顯著區別。650 K工況下IDT對高標號反應相對敏感,例如氫原子提取反應以及之后的低溫反應路徑所涉及的反應。而850和950 K工況下IDT對低標號反應也相對敏感,對應于小分子反應,該現象和NTC現象一致,即隨溫度的升高,與HO2相關的基元反應的重要性顯著增加。進一步由參考工況下的子空間訓練得到了共享子空間用于HCCI的點火成功概率分析,如圖8(a)中菱形符號所示,得出的點火成功概率隨曲軸轉角的關系如圖8(b)所示,點火失敗概率為37.9%。 圖8 點火延遲時間的活性子空間和共享子空間以及HCCI成功點火概率[53] Zhang等[68]對振蕩燃燒神經網絡模型系統開展了活性子空間分析。通過非穩態良好攪拌器(Perfect Stirred Reactor, PSR)模型模擬振蕩燃燒過程,得到了從混合氣摩爾分數、當量比、熱值、流率波動等8個輸入參數到目標量最高溫度的映射。他們得到了目標量的一維輸入子空間,通過分析對應活躍方向向量分量發現,增加混合氣中燃料質量分數尤其是CO質量分數將使最高溫度顯著增加從而提升燃燒系統的穩定性。同時當量比的影響也較大,在化學計量當量比附近減少當量比同樣會帶來最大溫度的提升。進一步,他們將子空間所對應的活躍變量替代原有的8個輸入變量,顯著簡化了神經網絡預測模型的結構形式,如圖9(a)所示。簡化后的神經網絡模型的預測結果如圖9(b)中雙點劃線所示,與原模型的預測值(藍色點劃線所示)幾乎一致。但是,神經網絡的訓練時間縮短了73%,單步預測時間加快了3倍。 圖9 振蕩燃燒神經網絡和溫度預測曲線[68] Briones等[69]采用活性子空間方法探究了小型化凹腔燃燒室幾何參數對燃燒的影響,共包含空氣入口參數、凹腔長度以及噴油位置15個幾何參數。在他們的分析中,沒有得到目標量(最大和平均溫度)所對應的低維活性子空間,但是,通過和Spearman敏感性分析得到的結果對比,發現活性子空間分析中最大特征值所對應的特征向量分量得到的參數的敏感性和Spearman秩相關系數得到的敏感性一致,說明在該情況下即使目標量不存在低維的輸入參數子空間,活性子空間分析中最大特征值對應的特征向量仍能夠用來做全局敏感性分析。 從以上綜述的研究進展可以看出,當前湍流燃燒模擬的活性子空間分析多集中在主控物理過程分析和正向不確定性的量化上,這些分析可以揭示特定目標量的的主控機制,從而探究湍流燃燒機理。但是,更進一步需要實現對湍流燃燒的調控,這就需要建模-計算-驗證形成閉環,如圖10所示。循環的右半側從物理模型到仿真計算結果,其中由模型和邊界條件帶來的不確定性即可通過活性子空間對海量參數的降維實現,同時如上文綜述的研究來探究物理問題的主控機制。循環的左半側則為,從仿真計算結果結合實驗數據或設計目標,反向調整輸入參數,實現對目標量的調控。 圖10 基于仿真計算的優化調控循環 在目標量調控的活性子空間研究方面,Constantine等[44]在對HyShot II超燃沖壓發動機仿真研究中,利用構建的一維單調響應面,確定了滿足安全運行所對應的目標量約束的操作參數范圍。如果實驗數據或設計目標是關于目標量的概率分布,此時參數調控問題為反向概率問題,即貝葉斯問題,在采用馬爾科夫鏈蒙特卡羅(Markov Chain Monte Carlo, MCMC)采樣時可以引入活性子空間方法,使采樣空間減縮到后驗概率密度空間的子空間中[33],從而提高反向參數調整的效率。湍流燃燒模擬反向問題可以得到滿足目標要求的輸入參數分布從而實現對湍流燃燒的調控。 活性子空間分析在湍流燃燒模擬中的應用,實現了對包括動力學模型參數、湍流燃燒模型以及邊界條件參數等海量輸入參數的降維,得到了復雜物理化學過程中的主控機制,有助于揭示湍流燃燒的機理,進一步實現對湍流燃燒的調控。主要工作和結論包括: 1)闡述了活性子空間方法和針對包含化學反應機理的湍流燃燒模擬的連續降維方法。該方法在對化學動力學參數降維中采用了替代模型,極大降低了所需湍流燃燒模擬次數。 2)總結了活性子空間方法和連續降維方法在Cabra火焰和B-K壁面射流火焰中的應用。揭示了湍流射流火焰中的關鍵化學反應以及主控物理過程的空間演化。 3)總結了模型燃燒系統的活性子空間分析,包括零維HCCI點火系統化學動力學主控機制分析、非穩態PSR振蕩燃燒的神經網絡系統的輸入參數降維,以及凹腔燃燒室幾何對湍流燃燒的影響。 4)對于湍流燃燒調控的活性子空間分析,可根據子空間中的低維響應面對輸入參數進行調整,從而調控湍流燃燒過程。另外,可以通過在活性子空間中采用MCMC采樣,開展反向概率研究,實現湍流燃燒調控。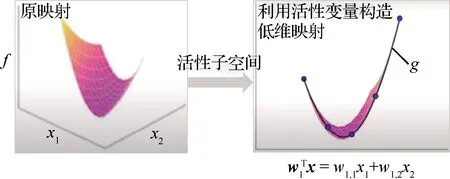

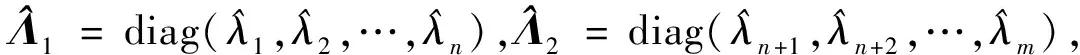

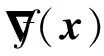
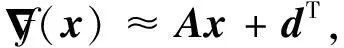

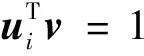
2 湍流燃燒仿真不確定性和主控機制分析

3 結果綜述和展望討論
3.1 化學動力學參數不確定性

3.2 化學動力學-物理模型參數不確定性

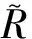

3.3 模型燃燒系統燃燒性能預測
3.4 討 論
4 結 論

