具有模糊失效狀態的渦輪盤疲勞可靠性及靈敏度分析

黃曉宇, 王攀, 李海和, 張政

1.西北工業大學 力學與土木建筑學院, 陜西 西安710072;2.西北工業大學 飛行器可靠性研究所, 陜西 西安710072

渦輪盤是航空發動機的重要組成部分，其主要功能是連接渦輪葉片以及傳輸運送所需功率。航空發動機渦輪盤長期處于高溫、高壓等惡劣工作環境下，并且隨著飛行狀態的不同承受著交叉載荷的作用，其危險點處會發生局部塑性應變，導致其極易發生疲勞失效。因此，對渦輪盤進行疲勞可靠性分析是保障發動機安全的重要手段。傳統的可靠性分析模型認為只有達到累積損傷極限時渦輪盤才會發生失效，從安全狀態過度到失效狀態是一個突變的過程，但是由于多種不確定性因素的存在，渦輪盤在疲勞損傷累積過程中也可能失效，其失效邊界呈現出模糊性。

近些年來，已有許多學者針對模糊可靠性分析進行了大量的研究，Cai等[1]提出利用模糊狀態假設來代替傳統的二元狀態假設，然后結合概率可靠性的分析方法，形成模糊可靠性理論。Mirakbari等[2]根據實際的數據，確定模糊隸屬度函數，提出一種基于馬爾可夫過程的方法來表示模糊失效概率。黃洪鐘[3]系統地分析影響結構可靠性的模糊性因素，提出結構模糊可靠性計算的統一模型，并定義幾種不同類型的隸屬函數。針對具有模糊失效狀態的可靠性分析算法方面，董玉革等[4]利用水平截集將模糊可靠性問題轉化為常規可靠性問題，并且使用數值的方法來求解模糊失效概率，但是其計算成本過大。李貴杰和宋軍等[5-6]將隨機變量積分區域離散化，使得每個積分區域內功能函數對模糊失效區域隸屬函數的取值近似相等，從而將模糊失效概率轉換成常規的失效概率，然后提出基于矩方法和靶點逼近的模糊可靠性算法。Feng等[7]將模糊失效概率等價轉換成一系列常規失效概率，并使用子集模擬法來重復計算一組總樣本對應的一系列常規失效概率，進而求解模糊失效概率。Yun等[8]利用Kriging模型對樣本空間進行分層，對模糊狀態區域內的點進行精確運算，從而有效地計算模糊失效概率。Zhang等[9]提出一種單循環Monte Carlo的方法來有效地估計模糊失效狀態下局部和全局可靠性靈敏度。

本文對渦輪盤進行疲勞可靠性分析，在此基礎上考慮渦輪盤失效邊界的模糊性，建立具有模糊失效邊界的渦輪盤疲勞可靠性分析模型。再利用積分轉換和高斯求積公式，將模糊失效概率轉化成一系列失效概率的加權和，并基于此建立模糊失效概率的全局靈敏度。最后利用改進的主動學習Kriging和Monte Carlo模擬相結合的方法(AK-MC法)同時近似多個失效面，提升計算效率。

1 渦輪盤低循環疲勞壽命可靠性分析

1.1 渦輪盤載荷簡化分析

以某航空發動機渦輪盤簡化模型為研究對象，依據實際結構的尺寸，根據渦輪盤循環對稱特性，選取渦輪盤的1/36部分作為研究對象。本文主要考慮渦輪盤運行期間的離心力和溫度載荷。其中離心力主要包括渦輪盤本身的離心力和渦輪葉片對渦輪盤的離心力。 在有限元分析過程中,渦輪葉片對渦輪盤的離心力負載在渦輪盤外側連接面上。

F=mrω2

(1)

式中:m是渦輪葉片的質量；ω表示不同飛行任務下渦輪盤的轉速,在最大、巡航、空轉下分別為1 200,1 100,600 rad/s。

實際飛行中,不同任務會導致發動機的工作狀態不同。本文選定的飛機發動機載荷譜周期為1 000 h,其環境混頻后的轉速循環壓縮譜如表1所示。

表1 轉速循環壓縮譜

此外,渦輪盤通常在高溫環境下工作,盤體上的溫度梯度會產生極大的溫度載荷。在本文分析模型中,只有渦輪盤心和盤緣處的溫度數據,盤體的溫度分布不明確,一般使用經驗公式對渦輪盤體的溫度進行插值。常見的經驗公式有線性插值和非線性插值,本文簡化了溫度載荷,使用線性插值來擬合渦輪盤體的溫度分布。

T=T0+KΔT

(2)

式中:T0為盤心溫度400℃;ΔT為盤心盤緣溫度差150℃;K為線性系數。渦輪盤在最大、巡航、空轉下的應力應變分布如圖1所示,最危險位置位于盤心處。

圖1 3種工作狀態對應的應力應變響應

1.2 渦輪盤低循環疲勞壽命模型

渦輪盤的失效模式復雜,其中低循環疲勞失效尤為顯著。本文考慮帶Morrow彈性應力線性修正的Manson-Coffin方程來計算疲勞壽命

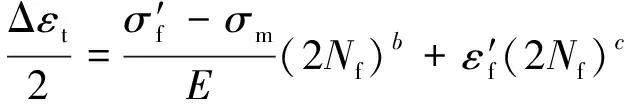
(3)

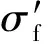
渦輪盤在工作時會受到多級循環載荷的作用,一般使用Miner線性累積損傷法則來計算累積損傷,渦輪盤的累積損傷可以通過(4)式來計算

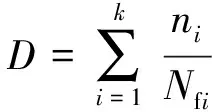
(4)

式中：k是循環載荷級數；ni是第i級載荷實際循環數；Nfi是第i級載荷下對應的疲勞壽命；D是多級載荷下的總損傷。

通常當累積損傷量達到損傷極限時,疲勞破壞發生。以此建立線性累積損傷模型的極限狀態方程,如(5)式所示

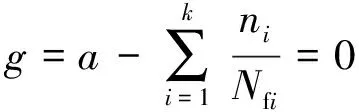
(5)

式中，a為疲勞破壞參數,一般情況下取值為1。

1.3 渦輪盤低循環疲勞可靠性

對于在惡劣工況下服役的航空發動機而言,其材料性能和載荷的分散性會導致疲勞壽命存在分散性。在對渦輪盤進行疲勞壽命分析的基礎上,綜合考慮渦輪盤材料性能和載荷的不確定性,進而可以定量地描述渦輪盤的疲勞可靠性。本文主要考慮材料性能和載荷的不確定性[10],其分布信息如表2所示。

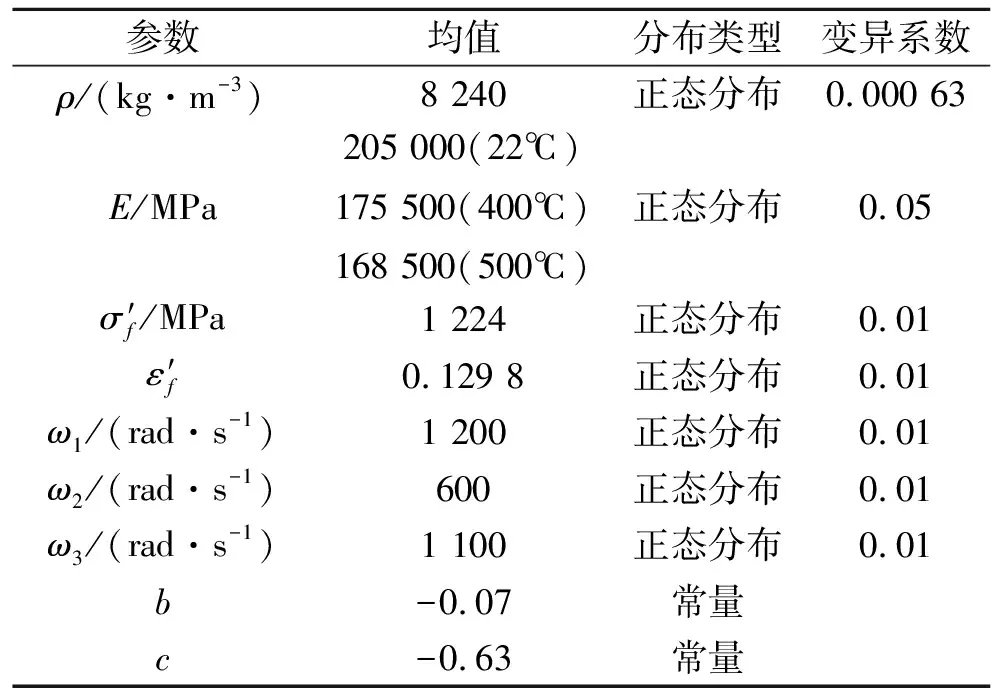
表2 隨機變量

根據(5)式的極限狀態函數,渦輪盤的失效概率可以表示為

(6)

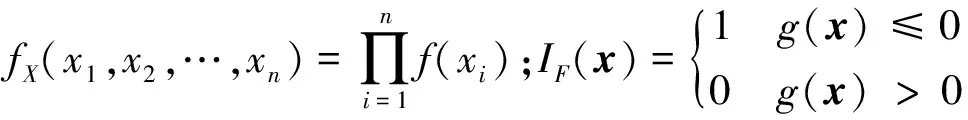
對于渦輪盤的可靠性分析問題,采用傳統抽樣方法計算效率低下。本文主要采用自適應代理模型法(active learning Kriging)來進行計算,該方法已經過許多文獻驗證[11-13],可以通過較小的計算代價得到精度較高的可靠性計算結果。因此,當設計壽命Tt=15 000 h時,利用AK-MC的方法只需要調用166次有限元分析結果就可以計算出渦輪盤的失效概率,失效概率計算結果Pf=0.008 56。

2 具有模糊失效狀態的渦輪盤疲勞可靠性及靈敏度

2.1 具有模糊失效狀態的渦輪盤疲勞可靠性

在結構疲勞壽命分析中,當疲勞累積損傷大于疲勞破壞參數時,疲勞失效發生。但實際過程中由于載荷加載順序以及小載荷強化損傷等因素的影響[14],疲勞破壞參數取值可能存在擾動,這將引起渦輪盤的安全域與失效域之間存在一個模糊的過渡邊界,導致載荷循環未達到預定疲勞壽命時也可能發生失效。為此本文考慮疲勞破壞參數具有模糊性,則(6)式中失效域指示函數可以表示為模糊指示函數(即,失效隸屬度)

(7)

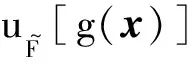
(8)

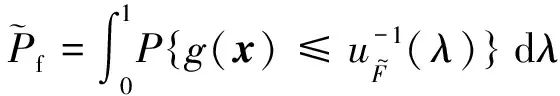
(9)

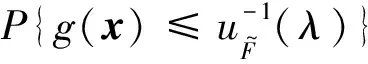
(10)

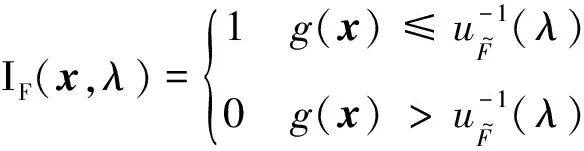
對于(9)式中的一維積分問題,可以利用高斯求積公式,將模糊失效概率轉化成一系列失效概率的加權平均

(11)

式中，ωj和λj分別是高斯積分權重和高斯積分點。

可以看到,對于渦輪盤模糊失效概率的計算需要大量調用渦輪盤的有限元分析結果,因此傳統的基于抽樣的可靠性分析方法難以有效計算,需要建立高效高精度的模糊可靠性分析方法。

2.2 基于模糊失效概率的渦輪盤全局靈敏度

基于失效概率的全局靈敏度可以衡量輸入變量在其整個分布域內變化時對結構失效概率的平均影響,能夠識別影響失效概率的關鍵因素。根據文獻[15]中的全局靈敏度指標定義,本文建立(8)式中的模糊失效概率全局靈敏度指標為

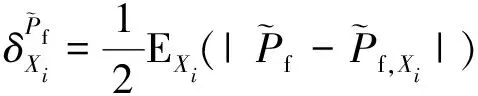
(12)

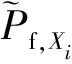
(13)

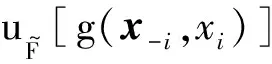
根據(9)式,條件模糊失效概率也可以轉換為一系列條件失效概率對于隸屬度的積分

(14)

進而,條件失效概率可以表示為高斯積分的形式

(15)

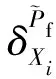
3 基于AK-MC的模糊失效概率及靈敏度分析方法

3.1 基于AK-MC的模糊失效概率分析方法

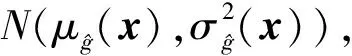
(16)

式中,S表示抽取的樣本池。對于所建立的Kriging模型,可以通過選取樣本池中U學習函數最小的樣本點對模型進行更新。根據文獻[20]中的收斂準則,通常取Kriging模型更新的收斂條件為:minU(x)≥2。

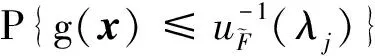
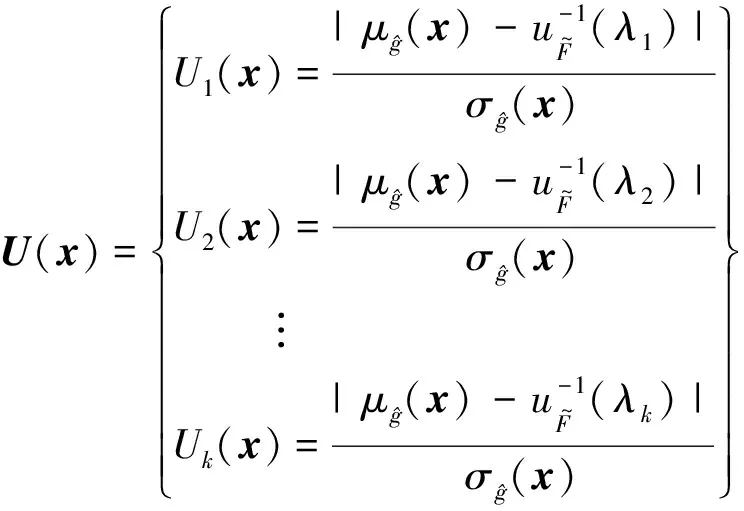
(17)

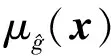
(18)

Kriging模型更新完成后,可以利用該模型對渦輪盤的響應進行估計,進而求解渦輪盤的模糊失效概率為

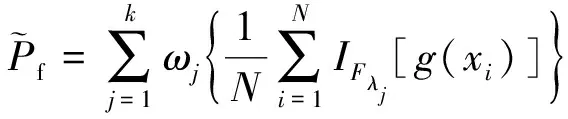
(19)

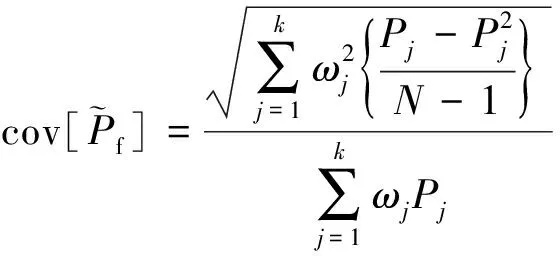
(20)

利用AK-MC對模糊失效概率進行分析,只需要調用渦輪盤的真實有限元分析結果來建立和更新Kriging模型,因此可以高效地得到計算結果。

3.2 基于AK-MC的模糊失效概率靈敏度分析方法

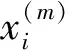
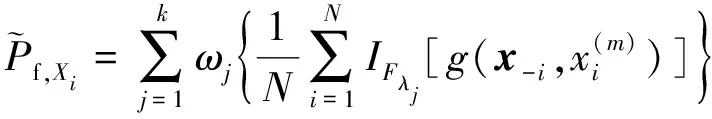
(21)

根據(12)式,模糊失效概率的全局靈敏度指標可以估計為

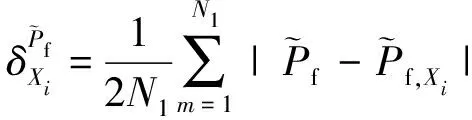
(22)

式中，N1為Xi的樣本個數,即(m=1,2,…N1)。

對于模糊失效概率的靈敏度計算,由于只是利用Kriging模型來估計條件模糊失效概率,沒有任何附加的有限元分析過程,因此其計算量和估計模糊失效概率的計算量相同。

4 分析及討論

4.1 渦輪盤模糊可靠性分析

針對渦輪盤的模糊失效概率,當設計壽命Tt為15 000 h時,采用上述改進的AK-MC可以對其進行分析計算。考慮到渦輪盤的模糊失效概率會隨著疲勞破壞參數擾動Δ的變化而變化,因此本文計算得到不同擾動下的模糊失效概率結果如表3所示。

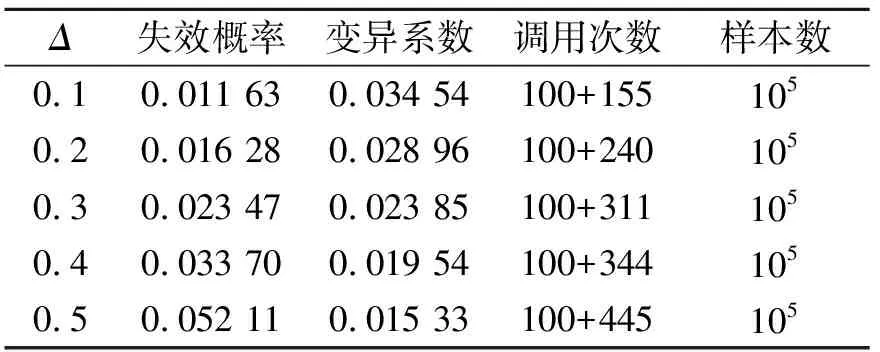
表3 模糊失效概率結果對比

表3中的結果表明:與傳統的失效概率(Pf=0.008 56)相比,渦輪盤的模糊失效概率相對較大,并且隨著疲勞破壞參數擾動Δ的增大而增大。這表明未考慮渦輪盤失效邊界模糊性的可靠性分析結果是偏危險的,并且隨著模糊邊界的擴大而增加。因此在開展渦輪盤可靠性分析時,應該考慮失效邊界的擾動情況,這樣得到的可靠性分析結果更為保守。

此外,由表3的結果可以看出,AK-MC方法只需要調用數百次的有限元分析結果便可建立Kriging模型,進而估算出渦輪盤的模糊失效概率,并且當樣本池取105時,模糊失效概率的變異系數都小于5%,這說明數值計算的結果已經收斂。同時,當擾動參數增加時,Kriging模型所需的更新樣本點也隨之增加,這也說明Kriging模型需要在更廣的失效邊界上獲得較好的預測精度。

4.2 渦輪盤靈敏度分析

針對(22)式中給出的模糊失效概率全局靈敏度,可以利用改進的AK-MC對其進行分析,并且無需額外的有限元分析過程。表4中給出了疲勞破壞參數擾動Δ從0.1變化到0.5時渦輪盤基于模糊失效的全局靈敏度指標計算結果。為了直觀表達,全局靈敏度指標分析結果對比如圖2所示。

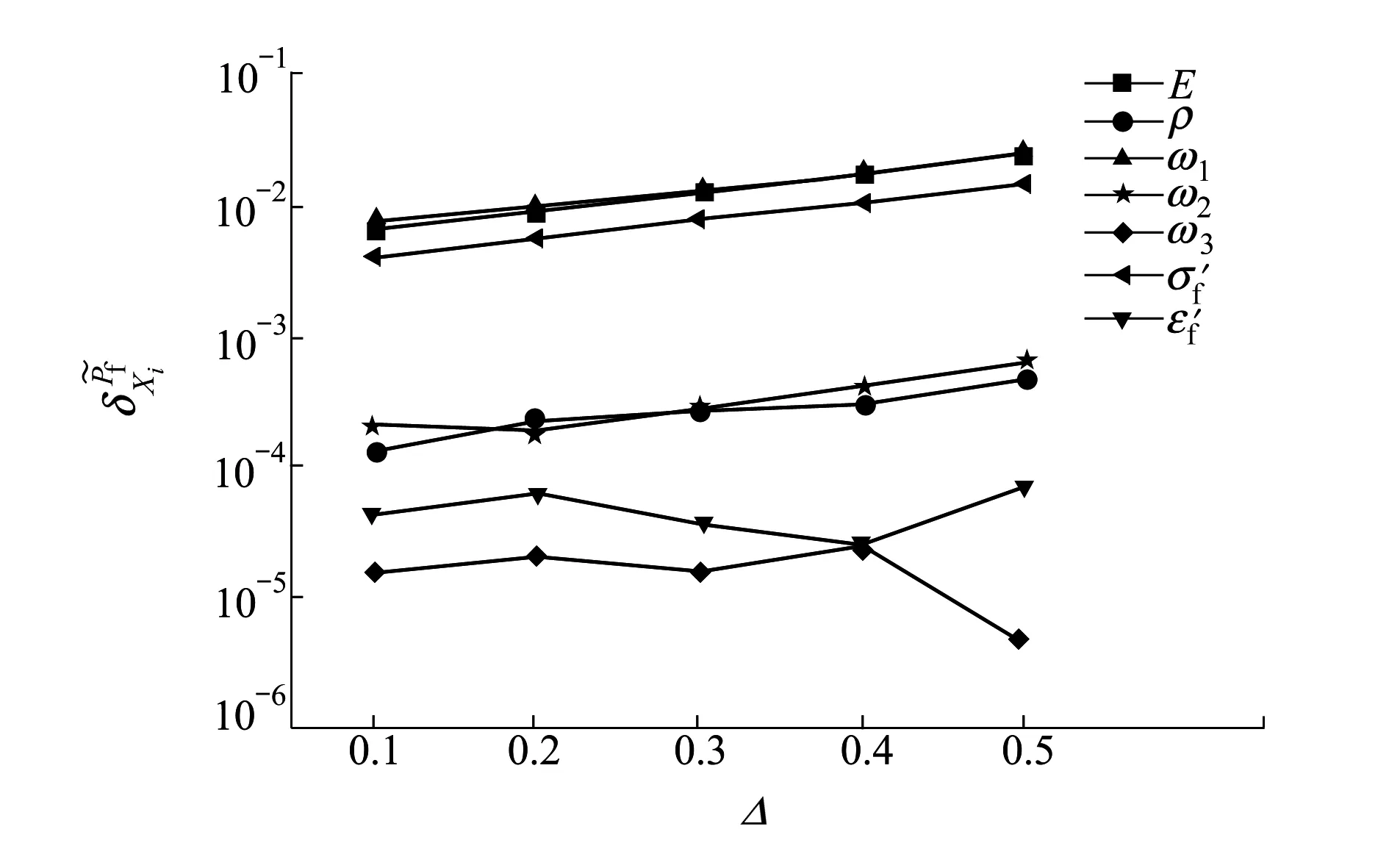
圖2 全局靈敏度指標對比圖

表4 全局靈敏度指標計算結果

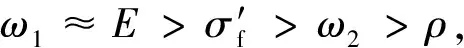
5 結 論

本文針對某GH4169粉末合金渦輪盤有限元模型，開展其疲勞可靠性分析研究。考慮渦輪盤失效邊界的模糊性，建立具有模糊失效邊界的渦輪盤疲勞可靠性模型，再利用積分轉換和高斯求積公式，將模糊失效概率轉化成一系列失效概率的加權和，并基于此建立模糊失效概率的全局靈敏度。

為了高效計算模糊失效概率及其靈敏度，本文利用改進的AK-MC法同時近似多個失效面，進而提升計算效率。與傳統失效概率計算結果進行對比，模糊失效概率相對較大，這說明傳統可靠性分析結果偏危險，并且隨著疲勞破壞參數的擾動 的增大而逐漸增大。此外，全局靈敏度的計算結果識別出影響渦輪盤結構安全性的3個關鍵參數。

盡管本文中考慮的失效邊界的模糊性，但對具體的擾動情況只是粗略給出其范圍并研究其影響規律，對于具體的疲勞失效機理還需進行更為深入的研究。