自動垂直泊車控制算法研究

石 晶，張春洲

（遼寧工業大學研究生學院，遼寧 錦州 121001）

1 引言

在當今高級輔助駕駛系統的多元化發展趨勢下，對高級輔助駕駛的研究已經不僅限于各大汽車制造企業及汽車設計公司，各高校已經逐漸開始對高級輔助駕駛進行更為深入的研究并進行相關模擬或實車實驗。自動泊車系統（APS）作為高級輔助系統下的一個重要分支，起著至關重要的作用。在駕駛員日常泊車時，由于泊車過程中駕駛員較大概率會產生緊張感，增大泊車難度，容易造成車輛碰撞，因此自動泊車系統可以給駕駛員提供很大便利。

自動泊車是通過探測車輛周圍環境信息來找到合適的泊車位，從而控制車輛的轉向和速度，使得車輛能夠自主駛入泊車位[1]。車輛在垂直泊車過程中，初始位置車身方向角在正負15°之間，且隨著離泊車位越近，車身方向角越大，在泊車完成時，車身方向角約為90°；泊車時方向盤打向泊車位方向，方向盤轉角先增大后減小，直至完成泊車。通過模糊邏輯控制器控制汽車運動模型中輸出的方向盤轉角，進而通過方向盤轉角改變車身方向角，實現車輛從初始位置到泊入車位的全過程，最后的仿真結果顯示上述論點可以得到驗證。

2 汽車運動模型搭建

根據大部分車輛長寬比例規定汽車長2500mm，寬1500mm，車速為5km/h。在汽車泊車過程中，汽車速度通常為（3～5）km/h左右，車輛產生很小的離心力，從而可以忽略輪胎側向力，故只考慮縱向作用力，不考慮橫向作用力，因此車輛滿足阿克曼轉向原理（Ackermann steering geometry）。阿克曼轉向原理指的是：汽車直線行駛時，4個車輪的軸線都互相平行，而且垂直于汽車縱向中心面；汽車設計時，為了避免汽車轉向時產生的路面對汽車行駛的附加阻力和輪胎的過快磨損，車輛在轉向時，要使所有車輪均為純滾動而無滑動[2]。研究車輛行駛過程中的運動軌跡，建立車輛泊車過程的動力學模型[3-4]，垂直泊車運動模型，如圖1 所示。圖1 中汽車自動垂直泊車運動模型參數：式中后軸中心點（Xa，Ya）；車身方向角θ，即車身縱向對稱平面與x軸間的夾角[5]；前輪轉角α；前后軸距離L，車輛寬度w。

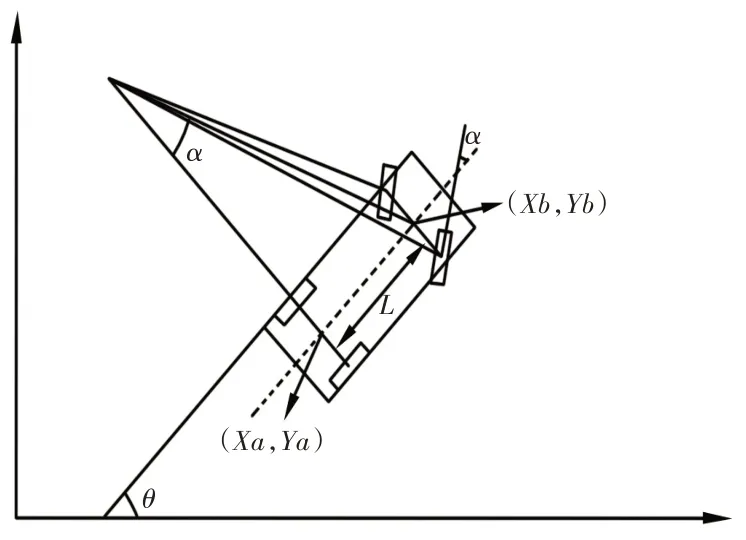
圖1 垂直泊車運動模型Fig.1 Vertical Parking Motion Model

汽車在低速泊車過程中，車輛沿后軸軸線速度為0[6]，可得：

為了實現汽車運動軌跡仿真，需知道汽車四個輪的坐標，經計算車輛車身四個頂點的坐標為[7]：

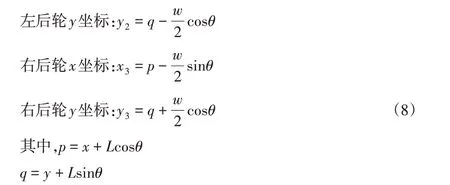
由上述算法可知汽車在泊車過程中的橫向速度、縱向速度和車身方向角的一階導數，通過對三個變量積分，可以得到汽車泊車過程中的橫向位移、縱向位移、車身方向角、前輪轉角四者的相互關系。在Simulink 中對此算法進行模型搭建，泊車運動模型，如圖2所示。

圖2 泊車運動模型Fig.2 Parking Motion Model

3 路徑規劃

根據駕駛員經驗可知垂直泊車流程如下：

（1）駕駛員將汽車泊到與泊車位前方的垂直位置，與邊線距離（0.5～1）m，若車身與泊車位不平行，則首先將車身擺正。

（2）駕駛員將方向盤向右打死，繼續泊車直至汽車與泊車位相平行；

（3）持續泊車直至汽車完全泊入泊車位。

按照以上流程可以確定的垂直泊車的運動軌跡和汽車在泊車過程中的路徑算法，如圖3 所示。確定泊車過程中車輪四個輪胎中心坐標及車身方向角位置變化關系，t為采樣間隔時間：

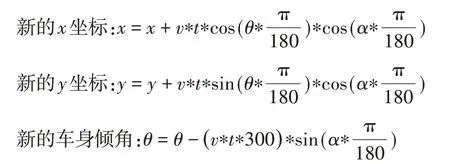
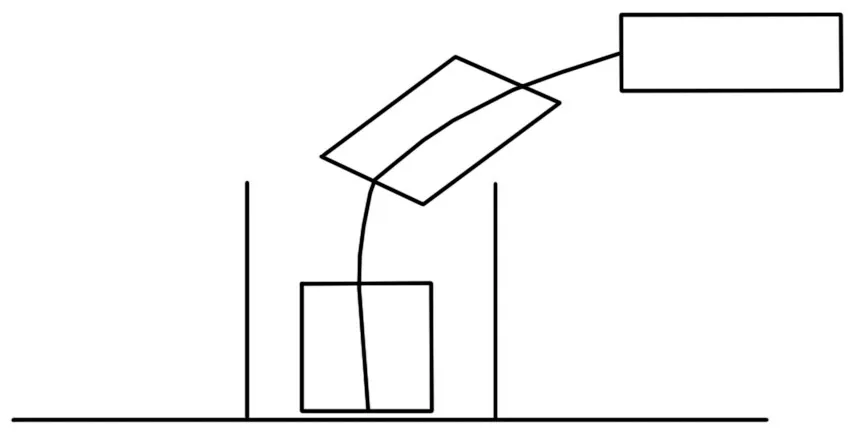
圖3 垂直泊車運動軌跡Fig.3 Vertical Parking Trajectory

4 模糊控制

利用MALAB 中的fuzzy 工具箱，通過修改輸入、輸出參數，完成自動泊車。綜合控制精度和響應速度兩方面考慮，在保證控制精度的前提下[8-9]，選取橫向位移x、車身方向角θ為模糊控制器的輸入，前輪轉角α為模糊控制器的輸出量。通過模糊控制實時控制泊車過程路徑規劃算法中的四個輪胎中心坐標及車身方向角，其中橫向位移、縱向位移、車身方向角、前輪轉角的相互關系已在汽車運動模型搭建中推導出，保證了汽車泊車過程中的平穩性、順滑性。

4.1 輸入量橫向位移參數

根據3中所建立的泊車位笛卡爾坐標系可知，水平范圍為（-20，120），即確定輸入x軸方向論域為（-20，120），模糊子集劃分為1個，{N}。N表示車輛位置橫坐標，隸屬度函數為梯形：[-56.9-36.6 39.21 40.7]。隸屬度函數，如圖4所示。

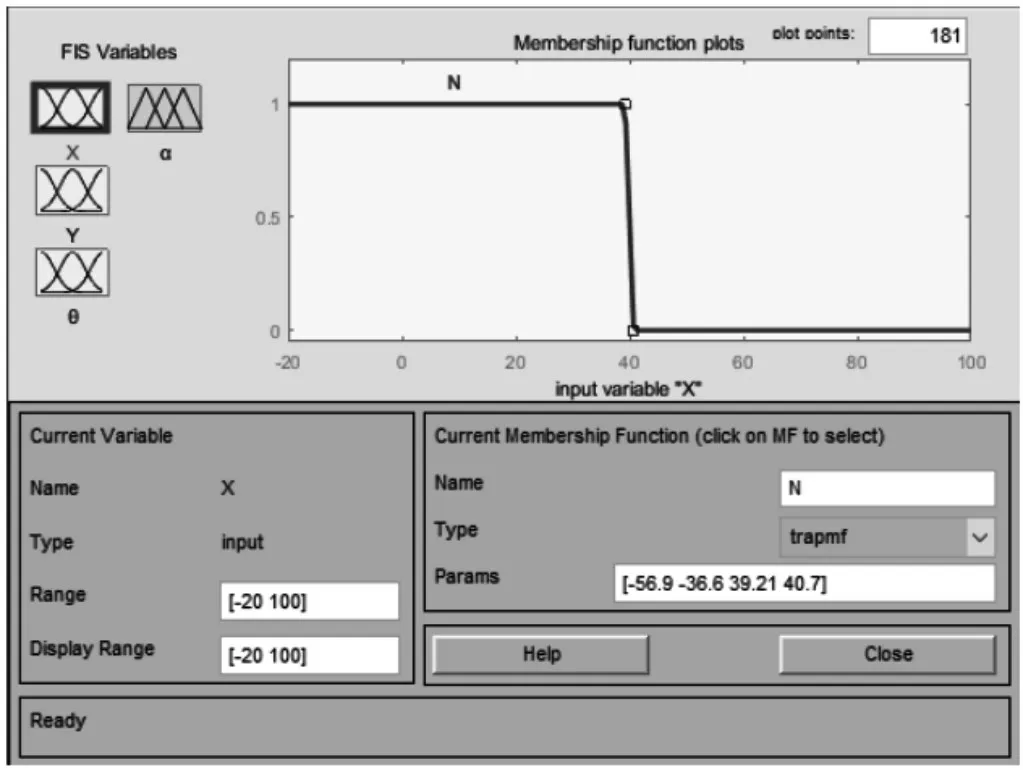
圖4 橫向位移隸屬度函數Fig.4 Lateral Displacement Membership Function

4.2 輸入量車身方向角參數

駕駛員在操縱車輛時會使車輛在道路中心線左右行駛，車身方向角與中心線偏移在正負15°以內，因此定義車身方向角論域為（-90，92），模糊子集劃分為4個，{N，PS，PM，PB}。N表示車身方向角小，隸屬度函數為梯形：[-105-97.46-8.83-1]；PS表示車身方向角適中，隸屬度函數為梯形：[-1.2-1 1 1.2]；PM表示車身方向角較大，隸屬度函數為梯形：[1 6.53 79.7 93.4]。PB表示車身方向角大，隸屬度函數為梯形：[88 89 90 91]隸屬度函數，如圖5所示。

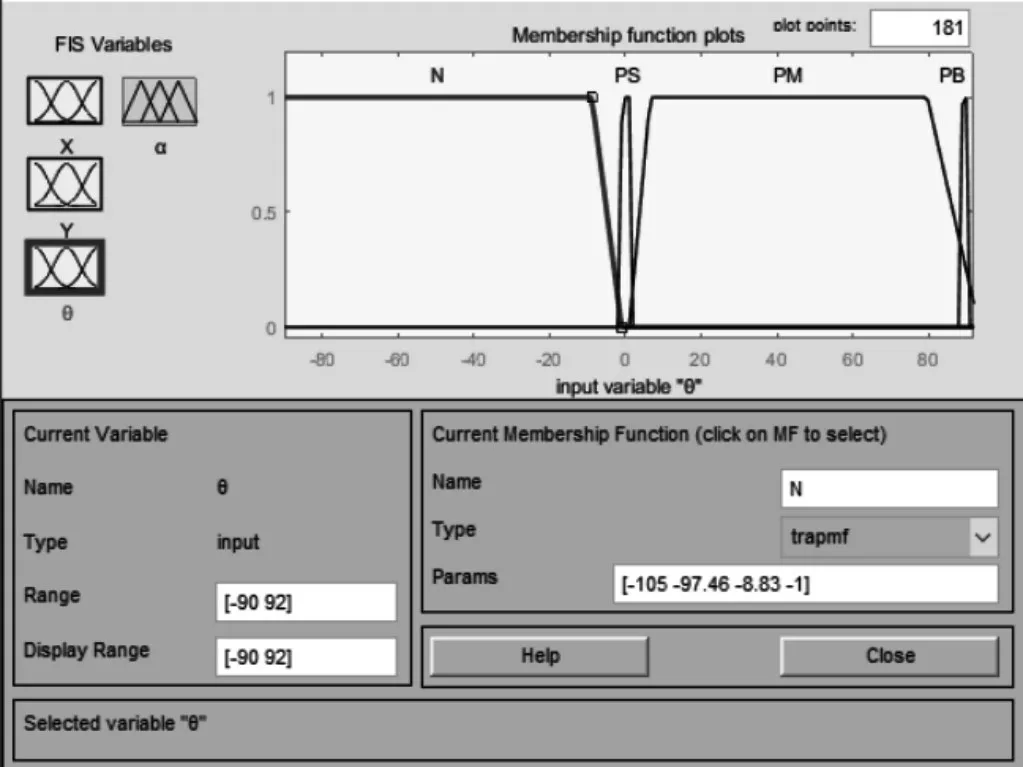
圖5 車身方向角隸屬度函數Fig.5 Body Orientation Angle Membership Function

4.3 輸出量方向盤轉角參數

定義方向盤轉角論域為（-45，45），模糊子集劃分為4 個，{NB，NS，Z，PB}。NB 表示負大，隸屬度函數為三角形：[-84.54-43.94-37.04]；NS表示負小，隸屬度函數為三角形：[-22.5-19.7-16.55]；Z表示零，隸屬度函數為三角形：[-0.833 0.2289 2.024]；PB表示正大，隸屬度函數為三角形：[39.5 44.17 45.4]。隸屬度函數，如圖6所示。

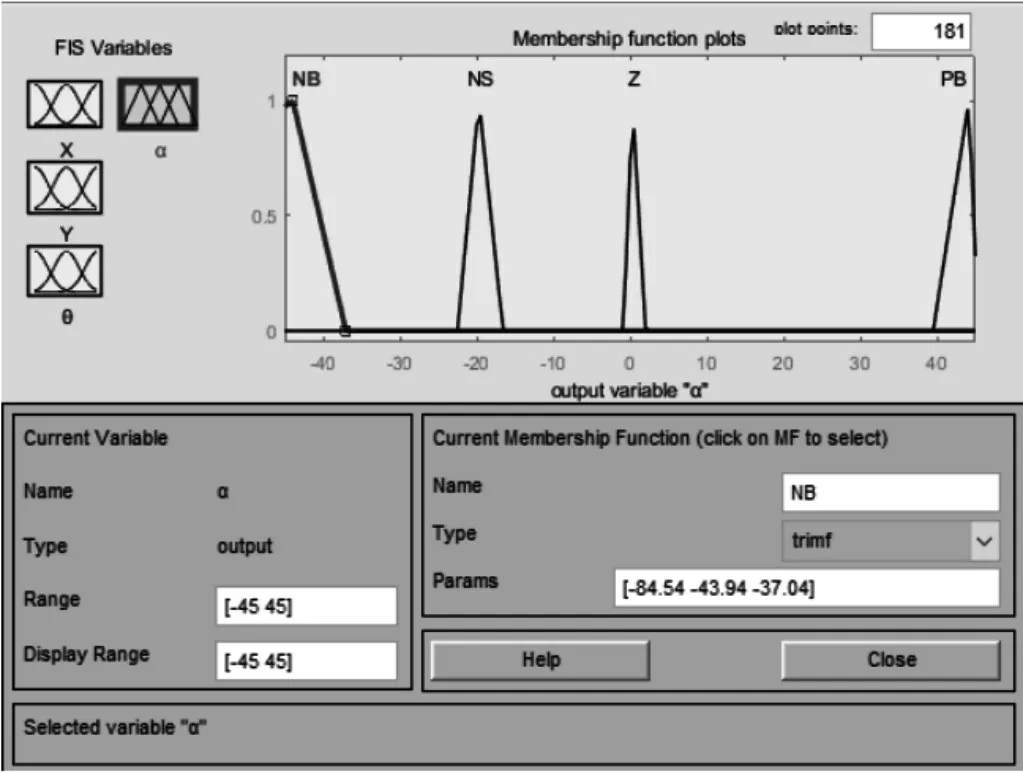
圖6 方向盤轉角隸屬度函數Fig.6 Steering Wheel Angle Membership Function

4.4 模糊規則

模糊規則是表示輸入量與輸出量之間的模糊關系，在設計模糊控制器時，對于駕駛經驗的模糊規則很多，使模糊控制算法實現很困難[10]，而且模糊規則數目的增加也加大了規則出錯的可能性[11]，對此提出建立精簡的模糊規則，制定的模糊規則，如圖7所示。

圖7 模糊規則Fig.7 Fuzzy Rules

因為在多數情況下，駕駛員在操縱車輛時會使車輛在道路中心線左右行駛，車身與中心線夾角在正負15°以內，因此車輛開始泊車時的縱坐標與泊車位縱坐標間距＞3000mm，泊車則順利完成。在仿真時將車輛初始位置固定，可以忽略縱坐標位置過近造成的不良影響，從而簡化模糊邏輯控制器。

5 仿真結果

車型選擇小轎車，車位長度為7m，車位寬度為2.5m，車輛寬度為1.8m，車輛長度為4.5m，對車輛的垂直泊車過程進行仿真。車輛初始位置縱坐標固定，初始車身方向角可在±15°內任意設置，以0°和5°為例，泊車速度為5km/h。根據搭建的汽車運動學模型及路徑規劃算法，在Matlab中搭建汽車、停車位等仿真環境，同時引入模糊邏輯控制器，模擬汽車的垂直泊車過程。

從圖8和圖10所示的車輛泊車軌跡可以看到汽車初始車身方向角在一定范圍內時，從初始位置到完成泊車過程平穩，通過軌跡可以看出車輛在垂直泊車過程中軌跡均勻，沒有特別明顯的波動跡象。通過對車身方向角初值的改變，經過對圖9 和圖11的分析可以發現，當車身方向角初值為0°時，汽車直接進行泊車，當車身方向角初值為5°時，汽車在泊車初始階段先調整車身方向角與泊車位呈垂直關系，進而繼續泊車，以保證汽車能夠完全泊入車位。

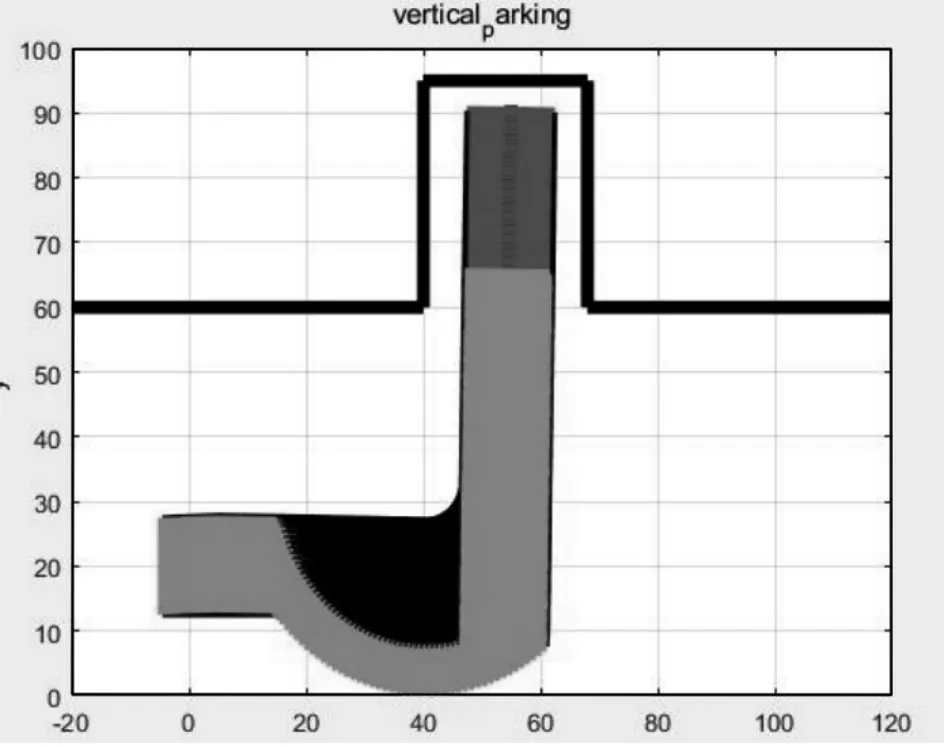
圖8 θ=0°仿真圖像Fig.8 θ=0° Simulation Image

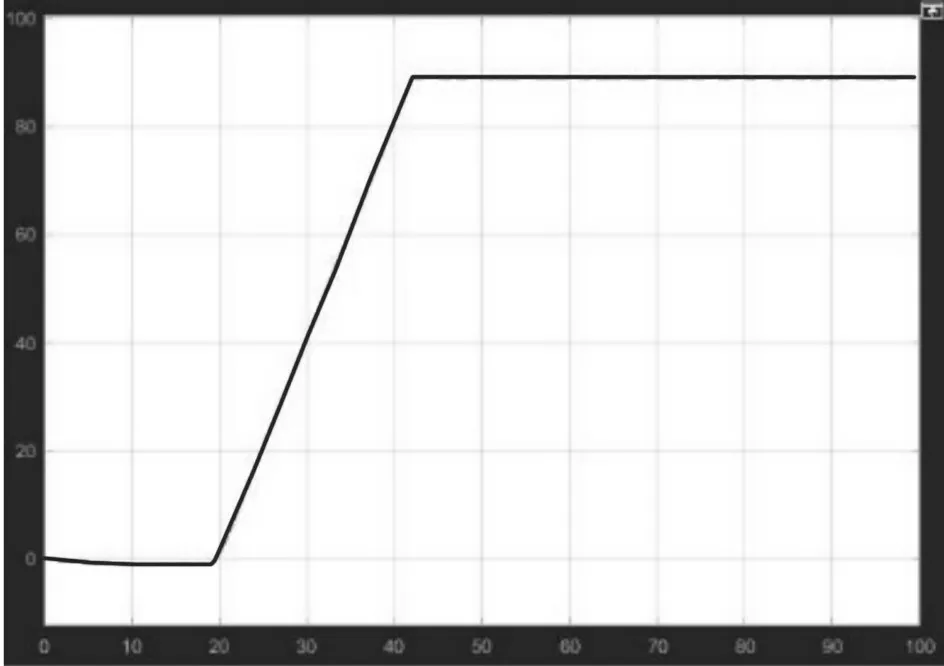
圖9 θ=0°車身方向角變化Fig.9 θ=0° Change of Body Direction Angle

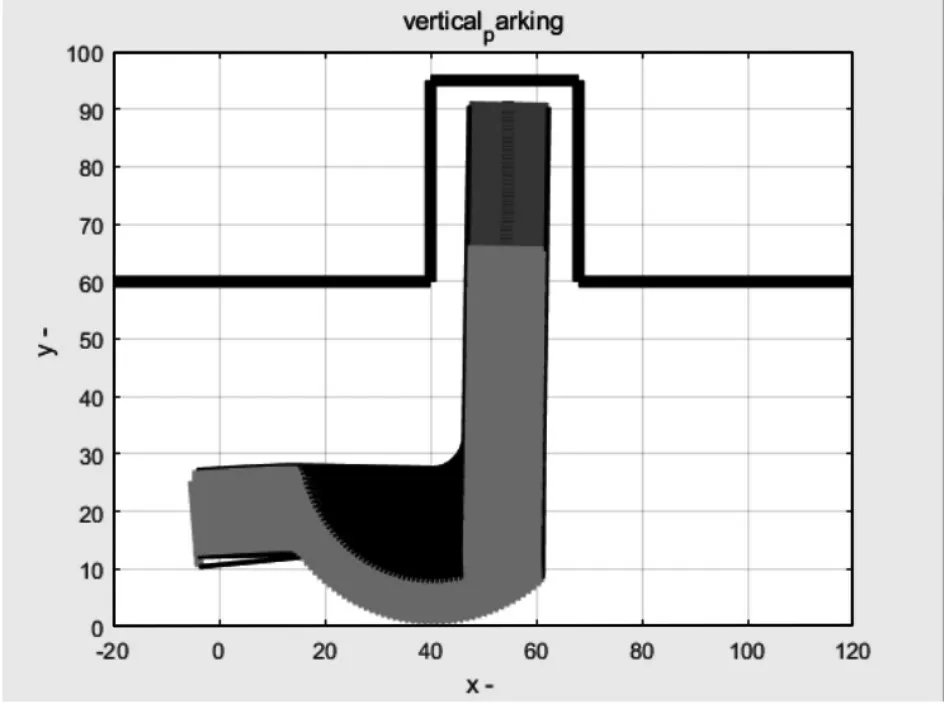
圖10 θ=5°仿真圖像Fig.10 θ=5° Simulation Image

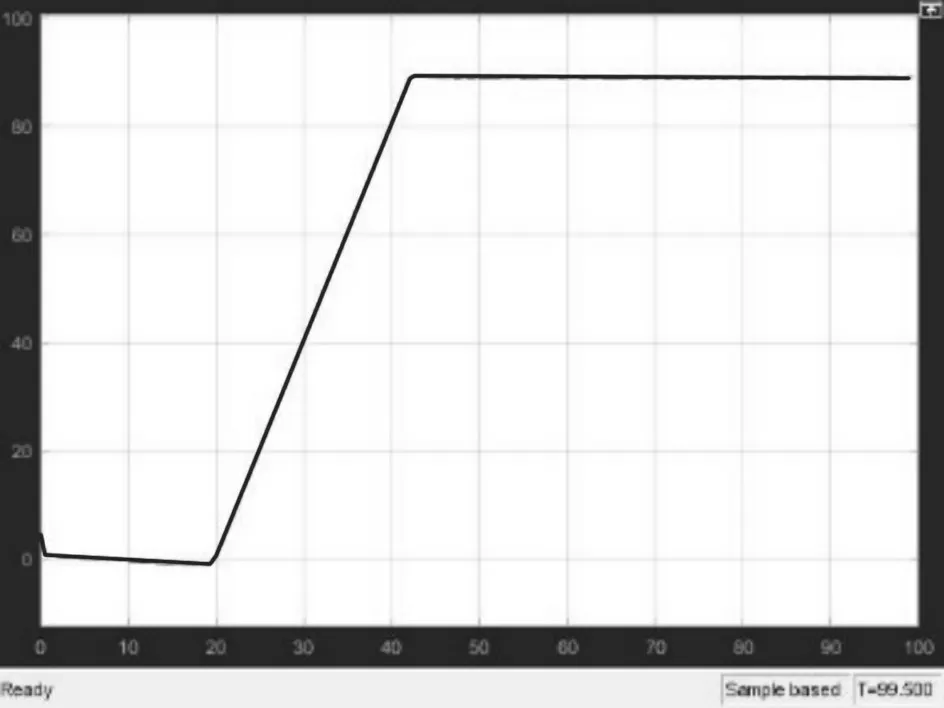
圖11 θ=5°車身方向角變化Fig.11 θ=5° Change of Body Direction Angle

6 結論

通過提出的一種基于模糊控制的垂直泊車三段式路徑規劃方法，從理論上驗證了方案的可行性，在Matlab中搭建仿真模型，設計較符合實際的模糊邏輯控制器，得到預期的仿真結果。仿真結果表明：汽車初始車身方向角在一定范圍內，初始縱坐標與泊車位距離＞3m，均可實現平穩、順滑的良好泊車，可以應用到不同泊車位、不同車型的垂直泊車中，為接下來在ADAS實驗平臺的仿真提供了可靠的基礎算法，為設計“自動垂直泊車”控制器提供參考依據。