網絡任務調度條件下機械加工誤差精準提取

宋小芹

（鄭州西亞斯學院，河南 鄭州 451150）

1 引言

在機械加工過程中，由于加工系統自身的老化和磨損，使得機械加工過程中會產生許多不可避免的誤差。如何對這些誤差進行精準提取和有效應對具有非常重要的意義。

在對加工誤差研究的過程中，多名專家學者提出了多種解決方法：利用回歸模型和時間序列AR模型、BP神經網絡[1]和RBF神經網絡[2]。

文獻[1]運用BP神經網絡對數控機床的誤差進行研究，確定了誤差參數和測量誤差的模型，在一定程度上避免了測量系統的不確定性，但是適用范圍較小；

文獻[2]利用RBF神經網絡提出了減小誤差、提高機械加工精度的方法，此方法具有較快的學習收斂速度[3]，適用范圍較廣，但是該方法計算過程較復雜，外插能力較弱、泛化能力較低。

為此，在現有的研究基礎上，結合網絡通信中的調度策略，對機械加工過程中的誤差進行具體的分析。

網絡通信調度可在檢測條件受限的情況下，合理分配網絡資源，控制傳輸速度，使優先級較高的信息在最短的時間內完成，從而提高網絡的利用率和誤差計算的精準性，減少誤差帶給機械設備的損害，保證設備的穩定運行。

2 網絡通信調度策略建立

2.1 靜態調度策略

靜態調度策略將網絡中所有的通信任務按照完成周期和緊急程度進行優先級[4]的劃分，優先完成周期短、加急的任務。

這里利用單調速調度算法（Rate Monotonic，RM），假設任務i的傳輸周期為hi，網絡傳輸模型為Li()ai，di，ci，bi，具體，如圖1所示。

圖1 控制任務的通信模型Fig.1 Communication Model for the Control Task

圖中：ai—任務的周期執行時間；di—相對時限；ci—任務傳輸時間；bi—阻塞時間；τi—傳輸總延遲。

那么網絡利用率可用式（1）定義為：

由于網絡系統中通信任務具有非強占性[5]，必須在一定時間內完成任務傳輸，這段時間內網絡僅為傳輸任務專用。

在網絡利用率已知的情況下，對一組獨立的具有周期性的非強占性任務，在滿足式（2）的條件下，就可用RM算法進行網絡調度。

周期較短的任務緊急程度越高，優先級也就越高（i=1表示最高優先級，i=N則表示最低優先級）。

先級較低的任務遇到的最大阻塞時間。

網絡通信系統中通常還會有一些不具有周期性的突發性任務，針對此類任務，系統將其定義為周期等于最小間隔時間的周期性任務。

對此類任務的傳輸過程，會預先設置好一個虛擬的周期任務[6]，在虛擬任務完成過程中，具有最高的優先級和假定的執行時間。通信系統一般會預留處理突發性通信任務。

2.2 動態調度策略

靜態調度策略中的通信任務優先級不受時間影響，而動態精度策略則受時間的影響。

最早時間優先算法（Earliest Deadline First，EDF）是比較常用的動態調度策略，在此算法下，任務的優先級會根據絕對時間限[7]的接近程度而發生變化，并不是一成不變的。

換句話說，系統會挑選絕對時間限最早的任務來優先完成。

針對非強占性任務，如果有n個周期性通信任務，每個通信任務的絕對時間限就是其周期，那么要利用EDF算法來劃分這些任務的優先級，需滿足的必要條件為：

2.3 變采樣和補償

在對機械加工誤差精準提取的網絡通信調度中，受系統帶寬的影響，可能在某個時期內會出現不可調度的情況，具體可通過延時和丟包通信[8]來確定不可調度的具體原因，通常可利用以下兩種方法來保證系統的穩定性：

（1）利用變采樣控制傳感器的采樣周期。如果采樣周期過長，系統的控制能力將會降低；如果采樣周期過短，則會導致網絡資源出現競爭、延時和數據丟失的情況，一定程度上也增加了網絡通信的負載能力。

（2）利用補償的方法構建虛擬采樣值，可控制系統采樣耗費的資源，減少系統負載。

3 機械加工誤差精準提取

在機械加工過程中，對于零部件的設計都須按照功能和結構要求來確定尺寸，進而加工設計[9]。在零件制造過程中，按照零件的結構特定和精度要求，選擇相應的加工工藝路線、工序定位基準和余量等進行加工，但是不可避免會產生誤差。

這里利用網絡通信調度對誤差產生的主要原因進行分析，并對誤差進行了精準提取，將其控制在合理范圍內，提高機械的加工精度。

計算機械加工過程中的誤差，應滿足式（4）要求：

式中：αU—原始尺寸AU的公差；λ—定位基準與技術資料基準補充的誤差，數值為二者之間的位置誤差s在AU方向上的映射；δP—計算定位誤差，數值為定位誤差δY在AU方向上的映射；δJ—夾具在安裝過程中產生的誤差；τ—加工誤差，通常包含機床誤差δe、刀具調整誤差（對刀誤差）δH、刀具誤差δD和變形誤差δB。

式（4）是計算加工誤差的基本理論，在實際的計算過程中，要特別注意各項誤差的方向問題，式中所表示的某一誤差在AU方向上的最大誤差值[10]。

當加工機械具有不止一個AU時，要對每一個誤差項都進行計算分析，且需一一對應滿足。

為了簡便計算，可將式（4）展開為：

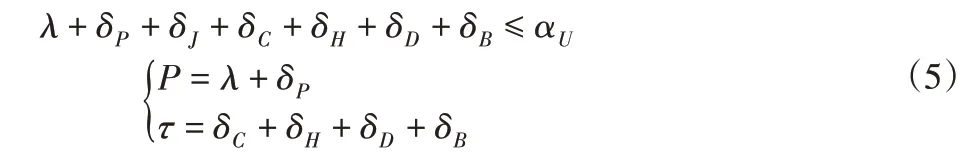
式中：P—工件安裝誤差。

δC、δD、δH、δB均屬于加工誤差，可利用這四項誤差來求合成誤差τ，在實際加工時，可選擇具體的加工方法來確定，一般采用的方法主要有以下2點：

（1）當構成加工誤差的實際誤差數目為兩項時，可直接利用求和方法來計算其加工誤差。

在鉆床加工、鏜床加工（用多刃刀具）、拉床加工及電火花加工中，可忽略δC和δB的影響，那么加工誤差表示為：

在車床加工、鏜床加工（用單刃刀具）、磨床加工及銑床加工中，忽略δD及δB的值，加工誤差可表示為：

由式（10）計算得出δ的值，再利用常用的經驗數據確定公差，根據實際情況利用式（4）加以驗算，最終確定加工系統中各項主要尺寸和技術條件的公差。

通過以上所述，如何計算使得式（4）控制在合理范圍內有了一定的了解，但在實際運用中，還是要具體問題具體分析，只有切合實際的解決方法才能保證式（4）的合理性。為了對式（4）中的各項誤差做進一步研究，利用直角坐標系線段相加的方法給出了圖解表示方法具體，如圖2所示。

圖2 加工誤差分析尺寸鏈Fig.2 Dimensional Chain of Machining Error Analysis

在圖2中，假設OX軸和OY軸為所要分析的機械原始尺寸方向，AU與各項誤差總和相減可得到精度儲備，用ε可表示為：

∑δ≈αU，即∑δ與αU的值相差不大，但是仍然不滿足式（4）的要求，這時可通過將其中個別誤差按車間實際可能達到的水平加以縮小來控制。

但是如果出現公差太小不能滿足加工要求時，則不建議通過該辦法來控制。可以將其中個別誤差單獨拿出來用均方根來計算合成誤差，再將其代入式（4）中，直到滿足∑δ ＜αU為止。

∑δ ＜αU，即滿足式（4）的條件，也說明了此時滿足機械加工精度要求。

4 仿真實例

為驗證這里方法計算加工誤差的精準度，將文獻[1]方法、文獻[2]方法與這里方法計算結果對比進行仿真實驗。實驗對象為軸承外圈將均方誤差(MSE)作為檢驗指標計算公式為：

式中：Q—結果輸出；

Qi—訓練樣本集輸出；

t—訓練樣本個數。

實驗結果，如圖3、表1所示。

表1 三種方法計算結果對比Tab.1 Comparison of Calculation Results of the Three Methods

圖3 原始尺寸與三種方法計算結果對比圖Fig.3 Comparison of the Original Size and the Calculated Results of the Three Methods

從圖中和表中可以看出，在樣本數僅為18個的情況下，本文方法相對于其他兩種方法有著更強的適應能力，計算結果與實際偏差值最接近，并且在對后3個序列進行誤差計算時，計算結果相對于其他兩種方法更接近實際值，計算精度更高。

計算結果表明，這里方法均方誤差為0.0352，優于文獻[1]和文獻[2]兩種方法的計算結果，提高了計算精度，在以上3種方法中效果最佳，且計算的值也更接近于實際值。為更直觀輸出不同方法的誤差提取精度，利用仿真軟件平臺輸出不同方法下同一軸承外圈的加工結果，利用文獻[1]方法、文獻[2]方法以及所提方法對軸承外圈加工誤差進行提取結果，如圖4所示。

根據圖4的實驗結果可知，以同一軸承外圈為實驗對象，文獻[1]方法和文獻[2]方法的加工誤差提取結果陰影面積較大，外圈的毛刺較為明顯，具有較大的提取偏差。

圖4 不同方法下誤差提取結果對比Fig.4 Comparison of Error Extraction Results Under Different Methods

相比之下，所提方法的誤差提取結果更為精準，提取的軸承外圈更圓滑，幾乎沒有出現較大偏差。實驗結果驗證了所提方法具有更理想的應用效果。

5 結論

利用網絡通信調度，提出了機械加工誤差精準提取方案。通過與其他兩種方法對比，取得了較為理想的實驗結果，對提高產品質量具有重要的作用。

（1）通過對網絡通信調度的分析，發現問題所在并給出解決策略，實驗結果得出均方誤差為0.0352，該方法將誤差值控制在合理范圍內，大大提高了計算精度和加工效率，降低了產品報廢率。

（2）此次仿真實驗對象將軸承外圈作為檢驗指標，檢測對象單一，不能廣泛應用到其他零件中。

（3）在今后的研究中，在進行機械加工誤差精準提取的過程中，需要深入研究提取前的工件和提取后的工件，準確測量工件的各項主要尺寸。