有向通信拓撲下海上無人集群分布式編隊控制

侯岳奇，梁曉龍*，張諾，陶浩，龔俊斌

1 空軍工程大學 空管領航學院 航空集群技術與作戰運用實驗室，陜西 西安 710051

2 中國人民解放軍31005部隊，北京 100094

3 中國艦船研究設計中心，湖北 武漢 430064

0 引 言

隨著無人航行平臺的迅速發展和任務需求的不斷拓展，多平臺的編隊控制技術受到廣泛關注。國內外相關學者在編隊控制方面展開了積極的研究，并在不同應用場景下取得了大量研究成果，包括無人機集群[1]、無人艇集群[2]和無人車集群[3]。根據實現思想的不同，經典的編隊控制方法主要可以總結為以下3種：基于領航?跟隨者[4]的方法、基于行為[5]的方法和虛擬結構法[6]。這些經典編隊控制方法雖然各有優缺點，但都難以滿足編隊控制分布式、自主化和集群化的需求。

近年來，基于一致性的方法通過圖論理論描述集群平臺之間的通信拓撲，并逐漸融合了其他經典方法，目前已發展成為編隊控制的主要方法。當前一致性編隊控制問題研究主要集中在一致性控制協議設計及其穩定性分析上。Dong等[7]采用內/外環結構建立了編隊控制框架，并基于一致性理論討論了時延、拓撲切換[8]、外部擾動[9]等條件下無人機集群時變編隊控制的穩定性和充要條件。Antonelli等[10]針對一階系統的時變編隊控制問題進行研究，討論了不同通信拓撲、包含飽和輸入約束等多種情況下的編隊全局收斂性，并用輪式機器人進行了驗證。Zhao等[11]對由無人機和無人車組成的異構集群時變編隊控制問題進行了研究，結果顯示編隊跟蹤誤差在有限時間內收斂了。上述研究均是針對連續時間系統展開，而針對離散時間系統方面的研究則相對較少。Zhang等[12]通過多步預測控制策略，實現了高階線性離散時間多智能體系統能夠快速收斂至固定編隊。Xu等[13]對具有一致通信時延和固定拓撲結構的二階離散系統的編隊控制問題予以了研究。但文獻[12-13]所研究的都是固定編隊控制問題，所得結論并不能應用于時變編隊情況。

由當前研究進展可以看出，一致性方法在連續時間系統編隊控制問題中已得到廣泛研究，但在實際應用中，因海上無人集群系統通常無法給出連續的控制指令，故將連續系統的結論應用到離散系統中會存在因控制參數不合理而使得系統不收斂的情況。針對離散時間系統編隊控制問題，現有文獻的研究主要集中在固定編隊控制方面，難以滿足海上無人集群的應用需求。為此，本文擬基于虛擬領航者思想，采用內/外環分層編隊控制結構，將一致性編隊控制方法應用到海上無人集群時變編隊控制之中。首先，基于離散時間系統進行系統建模，采用基于位置和速度誤差反饋的分布式控制協議；然后，在有向通信拓撲條件下，證明控制協議的穩定性，并給出期望構型可行性條件和控制協議參數及控制器更新周期約束條件；最后，仿真驗證理論結果的有效性。

1 預備知識及問題描述

1.1 預備知識

本文符號說明：1N(0N)表示所有元素均為1(0)的列向量，在不引起歧義的情況下，用1(0)表示元素全為1(0)的相應維數的矩陣或向量；IN表示N階單位矩陣；i 為虛數單位，即 i2=1。

考慮由N個平臺組成海上無人集群，包含無人艇和無人機，記為U1,U2,···,UN，記ZN={1,2,···,N}為平臺編號集合。集群的通信網絡拓撲可以用加權圖G=(W,E,A)來描述，其中W={ω1,ω2,···,ωN}為圖G的節點集，E={(ωi,ωj):ωi,ωj∈W}為邊集，A=[aij]N×N，為鄰接矩陣。若Ui能 夠接收到Uj的信息，則稱Uj為Ui的 鄰居，則在圖G中存在一條由節點ωj指 向節點ωi的 有向邊 (ωj,ωi)∈E。ai j為平臺Uj的 信息對平臺Ui的 權重因子，若 (ωj,ωi)∈E，則aij＞0 ，否則，aij=0 。若對 ?i,j∈ZN，有aij=aji，則稱G為無向圖，否則，G為有向圖。若存在一個有序的有向邊序列( ωi,ωi1),(ωi1,ωi2),···,(ωim,ωj)∈E，則稱圖G中存在由節點ωi到 ωj的有向路徑。若圖G中存在一個節點，且與其他任意節點之間都存在有向路徑，則稱圖G包含一個有向生成樹。圖G的拉普拉斯矩陣L=[lij]N×N定義為：

下文將給出分析海上無人集群編隊控制問題需要用到的基本引理1。

引理1[14]：對于包含N個節點的有向圖G，其拉普拉斯矩陣L具有如下性質：

1) 拉普拉斯矩陣L至少有一個零特征值，1N為特征值0對應的特征向量，即L1N=0N；

2) 僅當圖G包含有向生成樹時，0是L的代數重數為1的特征值，其他非零特征值均具有正實部；

3) 若圖G為無向圖且是連通的，則0是L的代數重數為1的特征值，其他非零特征值均為正實數。

1.2 系統模型

海上無人集群主要由無人艇集群和無人機集群組成，其運動空間涵蓋海面和空中。本文所指的無人機為旋翼無人機，其運動速度與無人艇基本匹配。由于平臺特性和運動環境的差異，因此無人機與無人艇的動力學模型不同。對于海上無人集群中的各平臺，考慮到位置控制的時間常數遠大于姿態控制，在僅考慮位置和速度的編隊控制中，可以把控制器解耦成內環和外環的分層結構分別進行設計[1]，如圖1所示。

圖1 內/外環分層編隊控制結構框圖Fig.1 Inner/outer loop layered control structure of formation

在內/外環結構中，外環為編隊構型控制層，可以根據期望構型、鄰居狀態、參考航跡等信息計算本機的控制輸入，從而使運動平臺以期望的速度到達期望的位置；內環控制則根據編隊控制層的輸出，結合動力學特性，對姿態/舵面、油門/推力進行控制。這種分層控制結構的相關理論和應用已經較為成熟，使得相關研究的重點可以集中到任務決策方法和外環控制律的設計及其穩定性分析上，從而提高了算法對于異構集群的兼容性。本文主要針對外環控制進行研究和分析，因此，在編隊控制層面上，將無人艇和無人機視為是一個質點系統，每個平臺的運動模型可以近似地采用二階積分器來描述，如式（2）所示。

在依靠跨域通信網絡的編隊控制中，狀態信息需要通過網絡進行周期性的交互和更新。考慮到通信網絡傳輸的數字采樣和時間離散特性，采用差分近似法對式（2）進行離散化處理，得到二階離散時間系統形式如下：

式中：xi(t)∈Rn，vi(t)∈Rn， 分別為t時 刻平臺Ui的位置和速度矢量，其中n為集群平臺運動空間維數；ui(t)∈Rn，為加速度控制輸入；t=t0+kδ，為控制器更新時刻，其中t0≥0和 δ＞0分別為初始時刻和控制器更新周期，k=0,1,2···。因上述離散系統在各維度上是解耦的，故所有結論均可從一維擴展到高維情況。本文選取n=1的情況進行研究。

1.3 問題描述

海上無人集群在執行作戰任務時，通常需要保持一定的隊形并按照期望航跡編隊航行，以實現無人集群協調運動和通信穩定連接。例如，在協同搜索、巡邏任務過程中，海上無人集群通常保持固定的編隊以增大探測范圍；在查證、定位任務過程中，需要多域多平臺持續環繞敵方平臺，此時，便需要保持時變編隊。期望航跡通常由多條直線段銜接組成，假設存在一個虛擬領航者U0按照期望航跡勻速運動，其期望航跡可以描述為以下離散系統：

式中：x0(t)∈Rn，v0(t)∈Rn，分別為t時刻期望航跡的位置和速度矢量； δ＞0，為航跡信息更新周期，與控制器更新周期相等。虛擬領航者并非實體平臺，其航跡信息不受其他個體航行信息的影響。在有向通信拓撲中，集群內部分個體能夠直接獲取虛擬領航者的期望航跡信息。

在不同的任務中，可能需要集群保持固定或時變編隊。考慮到理論研究工作的適用性，本文針對集群時變編隊控制問題展開了研究，得到的編隊控制器可同時適用于固定編隊和時變編隊控制。時變期望構型參數可用如下有界函數表示：

式中：fx(t)，fv(t)和fa(t)分別為編隊參考向量的位置、速度和加速度分量；fxi(t)，fvi(t)和fai(t)分別為集群個體Ui相 對于虛擬領航者U0的期望位置、速度和加速度矢量差。按照上述定義，虛擬領航者U0的 編隊參考向量為fx0(t)=fv0(t)=fa0(t)=0。對于時變編隊控制問題，上述參數是隨時間變化的，而對于固定編隊控制問題，其固定期望構型參數fx(t)為 常向量，fv(t)=fa(t)=0N+1。有關海上無人集群編隊控制的定義如下所示。

定義1：若集群實現了期望時變編隊構型f(t)，并保持了對期望航跡的跟蹤，則稱集群實現了期望構型和航跡跟蹤。集群實現編隊跟蹤控制穩定的充要條件為：對任意平臺Ui(i∈ZN)，有下式成立：

2 編隊控制協議設計

為便于描述，本節選取n=1的情況進行了研究，所得結論能夠通過Kronecker積推廣至高維情況。令集群位置向量為x(t)=[x0(t),x1(t),···,xN(t)]T，速度向量為v(t)=[v0(t),v1(t),···,vN(t)]T，控制輸入為u(t)=[u0(t),u1(t),···,uN(t)]T，代入式（3），整理得到離散時間系統狀態空間方程為

針對海上無人集群在有向通信拓撲下的分布式編隊跟蹤控制問題，對于任意平臺Ui(i∈ZN)，采用如下基于鄰居位置、速度信息的分布式控制協議：

式中， α,β＞0，分別為位置和速度反饋系數。為便于推導，將上述控制協議推廣到i=0的情況，容易得到u0(t)=0。 將控制協議式（8）代入u(t)中，整理得到

將式（9）代入式（7），系統狀態空間方程轉化為如下形式：

首先，令 ψxi(t)=xi(t)?fxi(t)?x0(t)，ψvi(t)=vi(t)?fvi(t)?v0(t)， 當i=0時，ψx0(t)=ψv0(t)=0。令ψx(t)=[ψx0(t),ψx1(t),···,ψxN(t)]T，ψv(t)=[ψv0(t),ψv1(t),···,ψvN(t)]T，ψ(t)=[(t),(t)]T，則海上無人集群實現期望構型和航跡跟蹤的充要條件式（6）可以轉化為

3 穩定性分析

定理1：具有有向通信拓撲的海上無人集群在控制協議式（8）的作用下能夠實現期望構型和航跡跟蹤的充要條件是：當且僅當對于任意i∈ZN，期望構型滿足如下可行性條件：

且以下線性離散時間系統漸近穩定。

證明：根據 ψ(t)的定義，可得

則有

將式（14）代入式（10），可得

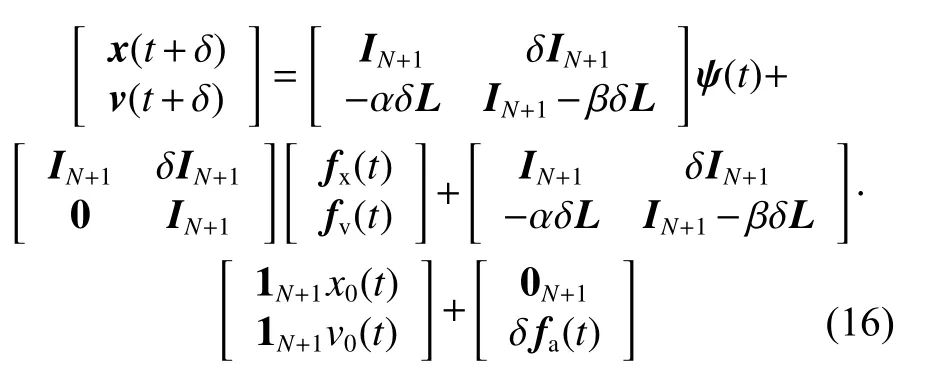
由式（3），可得

根據拉普拉斯矩陣的性質，有L1N+1=0N+1，則有

將式（16）～式（18）代入式（15），可得

海上無人集群能夠實現期望構型和航跡跟蹤的充要條件式（11）可以等價于

漸近穩定，且滿足可行性條件

可以很容易地驗證式（21）等價于式（12），結論得以驗證。

注釋1：由定理1可知，在控制協議式（8）的作用下，并非任意的期望構型都可以實現。式（12）稱為期望構型的可行性條件，表示期望構型的位置、速度和加速度分量必須滿足運動學特性。不僅如此，該可行性條件還給出了設計時變編隊構型的數學準則，在設計期望時變編隊構型時，需嚴格遵守該準則。

在滿足可行性條件式（12）情況下，只要線性離散時間系統式（13）漸近穩定，海上無人集群系統便可實現編隊控制和航跡跟蹤。為便于后文推導，令線性離散時間系統式（13）中的系統矩陣為

顯然，線性離散時間系統（13）的穩定性與矩陣Γ的性質有關。有關線性離散時間系統式（13）漸近穩定的充要條件在下文給出，在該過程中，需要用到以下結論。

引理2：0是拉普拉斯矩陣L的代數重數m的特征值，則1是矩陣Γ的代數重數2m的特征值。

證明：記拉普拉斯矩陣L的特征值為τi(i=1,···,N)， 設矩陣Γ 的 特征值為μ，則由特征值的定義，可知

則可求得矩陣Γ的特征值為

令 μi1,2=1，則有

因 α＞0 ，且僅當 τi=0時，上式成立，即僅當τi=0 時， μi1,2=1，故結論得以驗證。

定理2：當期望構型滿足可行性條件式（12）時，在控制協議式（8）作用下，具有有向通信拓撲的海上無人集群能夠實現期望構型和航跡跟蹤的充要條件是：矩陣Γ特征值1的代數重數為2，其他特征值均在單位圓內。

證明：對于充分性而言，虛擬領航者不接收其他集群個體的信息，故系統的拉普拉斯矩陣L可以表示為

式中，Llf和Lff為矩陣L的 子塊。令 ξ =[1,0]T，則有

式中，ξT為 矩陣L屬于特征值0的左特征向量。

根據線性方程組 (I2(N+1)?Γ)x=02(N+1)，可以很容易地驗證其解空間的維數為1，即矩陣Γ特征值1的幾何重數為1。并且，矩陣Γ特征值1的代數重數為2，故存在可逆矩陣P， 使P?1ΓP=J，其中J為 Γ的Jordan標準型，可表示為如下形式：

將式（32）代入線性離散時間系統式（13）中，記初始時刻為t0，可得

因為 ψx0(t)=ψv0(t)=0，則有

將式（34）代入式（33），可得

線性離散時間系統式（13）漸近穩定，由定理1可知，海上無人集群能夠實現期望構型和航跡跟蹤，定理的充分性得以驗證。

對于必要性，采用反證法進行證明。假設矩陣Γ特征值1的代數重數大于2，則至少有1個特征值的幅值大于1，即，故可進一步推導得到。線性離散時間系統式（13）非漸近穩定，顯然與海上無人集群能夠實現期望構型和航跡跟蹤相矛盾，定理的必要性得以驗證。

注釋2：由定理2可知，當矩陣Γ特征值1的代數重數為2，其他特征值均在單位圓內時，線性離散時間系統式（13）漸近穩定。而矩陣Γ的特征值取值與拉普拉斯矩陣L、 參數 α,β和控制器更新周期δ 相關。下文將進一步推導兩者之間的關系。

定理3：當期望構型滿足可行性條件式（12）時，在控制協議式（8）的作用下，具有有向通信拓撲的海上無人集群能夠實現期望構型和航跡跟蹤的充要條件是：通信拓撲具有以虛擬領導者為根節點的有向生成樹，且參數 α,β和控制器更新周期 δ滿足下式：

式中，λi為 拉普拉斯矩陣L除0以外的所有特征值，Re(λi)和 Im(λi)分別為其實部和虛部。

證明：對于必要性，由定理2可知，海上無人集群能夠實現期望構型和航跡跟蹤的充要條件是：矩陣L特征值1的代數重數為2，其他特征值均在單位圓內。結合引理2可知，拉普拉斯矩陣L僅有一個零特征值，記為 λ1=0 。 令 μ?1=s，由式（23），可得

矩陣Γ除特征值1外，其他特征值均在單位圓內，則有 Re(s)＜0。 設si1,si2為式（37）的一對根，則si1+si2=?βδλi，故有

根據引理1第2)條可知，通信拓撲包含有向生成樹。由于虛擬領導者不接收其他集群個體的信息，只要通信拓撲包含有向生成樹，虛擬領導者必為生成樹的根節點，因此，通信拓撲具有以虛擬領導者為根節點的有向生成樹。

將 σ=iω代入式（39），可得

由Hermite-Biehler定理可知，二次復系數多項式 γ(σ)是Hurwitz穩定的，且僅當下列條件成立時：

1）m(ω)=0 有2個不同的根，設為m1＜m2；

2)n(ω)=0 的單根n1滿 足m1＜n1＜m2；

3）m(0)n′(0)?m′(0)n(0)＞0。

將上述條件代入式（41），可得

求解不等式組（42），可得

定理的必要性得以驗證。

對于充分性，因為通信拓撲具有有向生成樹，由引理1的第2)條可知，拉普拉斯矩陣L僅有一個零特征值。根據引理2，可得矩陣Γ特征值1的代數重數為2。通過必要性的證明過程可知，當α,β,δ 的取值滿足式（36）時，g(μ)的 解滿足 |μ|＜1，即矩陣Γ除特征值1外，其他特征值均在單位圓內。由定理2可知，海上無人集群能夠實現期望構型和航跡跟蹤，定理的充分性得以驗證。

注釋3：系統的穩定性與控制協議參數 α,β、控制器更新周期δ和拉普拉斯矩陣L的特征值λi直接相關。在固定通信拓撲下，可以直接求得拉普拉斯矩陣L的特征值λi，進一步確定符合不等式組（36）的 α,β,δ取值，可使系統穩定[15]。文獻[16]指出，在拒止環境中，通信組網鏈路的可靠性將大幅下降，通信鏈路頻繁斷開，因此需要研究切換拓撲情況下的編隊控制。針對通信拓撲變化的情況，可能會導致不等式組(36)不成立，此時，需要重新確定參數取值，確保編隊控制的穩定性。

本文提出的編隊控制方法同樣適用于無向通信拓撲情況，下面，將不加證明地給出如下結論。

推論：當期望構型滿足可行性條件式（12）時，在控制協議式（8）的作用下，具有無向通信拓撲的海上無人集群能夠實現期望構型和航跡跟蹤的充要條件是：無向通信拓撲連通且參數 α,β和控制器更新周期 δ滿足

4 仿真分析

本節將通過數值仿真對所提出的編隊控制方法進行驗證。設定海上無人集群由1個虛擬領航者、2架無人機和7艘無人艇組成，并假設平臺在編隊航行過程中高度不變，只考慮水平面的運動。仿真中涉及到的位置、速度、加速度的單位分別為m，m/s和m/s2。集群平臺之間的有向通信拓撲圖G如圖2所示。

圖2 海上無人集群通信拓撲示意圖Fig.2 The communication topology of UMV swarms

顯然，有向通信拓撲包含以虛擬領航者為根節點的有向生成樹。編隊隊形信息矩陣為

設計海上無人集群的期望構型如圖3所示，其中7艘無人艇組成楔形編隊，2架無人機在無人艇編隊上空并排航行。

圖3 海上無人集群期望構型示意圖Fig.3 The expected formation of UMV swarms

航行過程中，當虛擬領航者運動轉向時，期望構型參數是實時變化的。根據虛擬領航者的位置、速度信息和隊形信息矩陣Fd，可以計算得到實時的期望構型位置參數。結合定理1給出的編隊可行性條件式（12），可令

通過式（46），可實時迭代求出期望構型的位置、速度和加速度信息。根據文獻[15]給出的參數選擇方法，首先計算拉普拉斯矩陣的特征值，設置 α=0.2,β=0.4。代入不等式方程組（36）中，可計算得到控制器更新周期的約束條件為δ＜0.5657。為兼顧系統穩定時間和通信代價，這里取 δ=0.5。

圖4給出了仿真中海上無人集群編隊軌跡的俯視圖和側視圖，其中紅色細實線為虛擬領航者，正方形和圓圈分別為無人機和無人艇。由圖4(a)可以看到，集群在初始位置時并沒有形成期望編隊，存在一定的位置偏差，但在編隊控制器的作用下，逐漸生成期望編隊。生成期望編隊后，在虛擬領航者直線運動或轉彎運動的情況下，海上無人集群均能始終保持期望編隊。由圖4(b)可以看到，無人機在500 m高度飛行，能夠與水面無人艇保持期望編隊，驗證了所提編隊控制器的有效性。為了更加清晰地展現編隊控制過程，圖5給出了不同時間段的集群編隊運動軌跡。

圖4 海上無人集群編隊軌跡圖Fig.4 The formation path of UMV swarms

圖5 海上無人集群編隊過程圖Fig.5 The formation process of UMV swarms

由圖5可見，在初始時刻，集群編隊軌跡存在一定的波動，這是因為集群在初始位置時并未形成期望的編隊，存在一定的位置偏差。當集群編隊航行1 000 m后，編隊生成并基本保持穩定。若編隊在直線段航行時，編隊誤差幾乎接近于0；而在轉彎段時，1號艇的軌跡與虛擬領航者并沒有完全重合，存在一定的穩態誤差。為了直觀分析編隊誤差隨時間變化的情況，圖6給出了編隊位置誤差和編隊速度誤差隨時間變化的曲線。

由圖6可見，集群初始狀態與期望編隊存在一定的偏差，故在初始時刻位置和速度誤差較大，至150 s左右時位置和速度誤差基本能夠收斂至0。當虛擬領航者開始執行轉彎動作時，編隊位置誤差會出現一個10 m的波動，然后在轉彎過程中保持5 m的穩態誤差。而在虛擬領航者開始或結束轉彎時，編隊速度誤差會出現一個10 m/s的波動，約在5 s內收斂至0。圖7給出了仿真中海上無人集群各個平臺速度隨時間變化的曲線，圖中Vx，Vy分別為X，Y方向的速度。

圖6 編隊位置和速度誤差隨時間變化曲線Fig.6 Time histories of formation position and velocity error

由圖7可見，在初始時刻，因編隊誤差導致控制量較大，從而使得初始時刻的速度變化較為劇烈，且存在一定的超調。隨著編隊誤差的逐漸降低，海上無人集群平臺的速度與虛擬領航者逐漸趨于一致。當虛擬領航者轉彎時，其他平臺的速度會發生較為劇烈的變化，并迅速趨于穩定。在轉彎過程中，各平臺的速度并沒有與虛擬領航者保持一致。因為在轉彎過程中需要保持編隊，而這會導致轉彎半徑不同，從而使得轉彎過程中的速度存在一定的差異。在直線段航行時，所有平臺的航行速度與虛擬領航者的速度保持一致，實現了穩定的編隊保持。

圖7 海上無人集群速度隨時間變化曲線Fig.7 Time histories of velocity of UMV swarms

5 結 語

本文研究了海上無人集群一致性分布式編隊控制問題，采用基于位置和速度反饋誤差的控制協議，分別給出了無向及有向通信拓撲條件下控制協議參數和控制器更新周期的約束條件，所得結論適用于固定和時變編隊控制。結果表明，集群實現編隊控制穩定的條件較為嚴格。當有向通信拓撲存在以虛擬領航者為根節點的有向生成樹，且控制協議參數、拉普拉斯矩陣的特征值和控制器更新周期需耦合滿足一定的約束條件時，才能實現編隊控制的穩定。本文研究沒有考慮通信時延的影響，這將在后續的工作中進一步深入探討。