基于Ciscrea AUV耦合模型的H ∞魯棒控制器設計

劉艷，馮旭琛，楊睿，黎明，馮一飛

中國海洋大學 工程學院，山東 青島 266100

0 引 言

自主式水下航行器（AUV）因其靈活性和自主性被廣泛應用于海底資源勘探、水下打撈以及海洋測繪等領域[1]。如何快速實現對AUV的精確控制一直是亟待解決的技術難題[2]。通常，AUV控制方法可分為基于模型控制和無模型控制。基于模型控制方法是通過精確揭示AUV所遵循的物理規律和運行機理，在先進的運動控制方法基礎上，可以解決風、浪、流擾動下無模型控制方法難以實現的AUV精準控制問題[3-4]。AUV運動學與水動力學模型具有非線性、參數不確定性以及各自由度間的耦合性特點，因此，AUV運動控制系統的設計具有挑戰性。

Yang等[5]采用H∞魯棒控制方法解決了Ciscrea AUV單自由度艏搖模型的非線性和不確定性問題。Rosendo等[6]基于準滑模調節的約束補償算法和比例微分控制算法，實現了Ciscrea AUV艏搖和垂蕩雙自由度控制。Guerrero等[7]在AUV六自由度數學模型上設計了去耦合控制器，但前期工作均未考慮耦合參數對控制結果的影響，多自由度耦合控制問題未得到解決。

H∞不確定集合控制方法具有魯棒性特點，對AUV模型中的不確定性參數不敏感，其控制性能不受擾動和參數變化的影響，可有效解決多自由度耦合控制問題。根據H∞魯棒控制原理，滿足魯棒穩定性及魯棒性能要求是設計AUV魯棒控制系統的兩個關鍵因素。首先，AUV模型中的不確定性參數可表述為不確定集合。根據小增益定理，具有不確定集合作用的閉環系統其魯棒穩定性等價于標稱閉環系統的內部穩定性，且阻尼、附加質量等參數的不確定性分量均可視為不確定集合并予以處理。其次，若AUV模型魯棒控制器結果滿足H∞魯棒性能要求，則控制器可以保證AUV具有良好的運動控制性能（例如跟蹤、干擾抑制和能量最小等），而H∞控制器綜合是設計求解H∞魯棒控制器的關鍵。

為此，Zames[8]以單輸入單輸出（single-input single-output，SISO）為對象，提出了基于頻域的H∞綜合方法，Doyle和Ball等[9-10]面向多輸入多輸出（multi-input multi-output，MIMO）對象，提出了基于狀態空間的DGKF（Doyle-Glover-Khargonekar-Francis）方法。這兩種方法都可通過求解代數Riccati方程（ARE)得到H∞綜合控制器，但Ciscrea AUV模型存在虛軸附近的極點，采用ARE方法實現H∞控制器綜合時，其廣義被控對象不滿足對應的正則約束條件，而采用基于內點法的線性矩陣不等式(linear matrix inequality, LMI)方法則可完成[11]。不同于ARE方法，LMI方法的正則約束條件較少，可直接求解ARE奇異問題[12]。

基于以上考慮，本文將針對Ciscrea AUV四自由度非線性數學模型的魯棒控制問題，從耦合控制角度，提出H∞綜合控制器設計方法，以實現在外部干擾下的AUV三維軌跡跟蹤與艏搖控制。首先，通過攝動法將Ciscrea AUV二次非線性阻尼作用和慣性矩陣的參數不確定性轉化為不確定集合，并得到廣義系統。然后，針對耦合的廣義系統，利用H∞綜合方法在穩定的魯棒控制器上優化閉環系統性能，通過MATLAB軟件提供的LMI工具箱[13-14]求解魯棒控制器。最后，模擬外部干擾下的三維軌跡跟蹤和艏搖控制場景。

1 Ciscrea AUV數學模型

本文利用MATLAB完成了Ciscrea AUV數學模型沿螺旋線下沉的仿真。由于僅涉及橫蕩、縱蕩、垂蕩和艏搖這4個方向的運動，故只針對Ciscrea AUV四自由度數學模型進行控制仿真。表1所示為Ciscrea AUV數學模型的運動參數。

表1 Ciscrea AUV四自由度數學模型的運動參數Table1 Four-DOF kinematic parameters of Ciscrea AUV

Ciscrea AUV模型的速度向量和位置向量分別表示為V=[u v w r]T和η=[x y zψ]T，已知其水動力模型為

式中：MRB和MA分別為Ciscrea AUV模型的慣性矩陣和附加質量矩陣；D(|V|)為阻尼系數矩陣；g(η)為 回復力；τpro為 推進器輸出的推力；τenv為外部干擾力（風、浪、流）。

在不考慮橫搖和縱搖自由度的情況下，控制系統可實現AUV運動控制。假設AUV的姿態始終與重力垂直，無需考慮重力與浮力的相互作用，則g(η)可忽略不計。但是，AUV受到的外力包括了推進器輸出的推力τpro和 外部干擾力 τenv，其水動力模型又可寫為

基于上述AUV模型，考慮質量變化對模型參數的影響。其中，MA僅與AUV的外形有關[15-16]，在實際工程中，AUV搭載的配件（例如相機、機械臂等）對其外形的改變可忽略不計，故MA不受影響。對于形狀規則的物體，MA可由經驗公式直接計算。然而，Ciscrea AUV是典型的具有復雜外形和開放架構的AUV，經驗公式并不適用。因此，文獻[17]通過流體計算軟件WAMIT計算得到了如下MA，詳細計算過程可參見此文獻。

Ciscrea AUV模型的慣性矩陣寫為：

式中：m為 AUV的自身質量；Izz為AUV繞z軸的轉動慣量。

由Solidworks軟件可計算得到MRB如下：

鑒于AUV質量變化會影響MRB[18]，故假設MRB具有30%的不確定性，可得到如下含不確定性的慣性矩陣：

H∞綜合方法通常適用于線性系統，需要對AUV模型進行線性化。因此，本文采用攝動法[19]將阻尼系數矩陣中的二次非線性作用轉換為不確定集合?d，其中不確定性的變化主要源于AUV作業速度的變化。已知：

式中：Dl為 線性阻尼系數矩陣；Dn(|V|)為非線性阻尼系數矩陣，Dn(|V|)=Dndiag(|V|T)。通過模型辨識實驗、STAR-CCM+和ANSYS-CFX這3種方法均可辨識得到四自由度水動力模型的阻尼參數，并取平均值作為最終的參數結果，具體如下[17]：

AUV在整個作業過程中，其速度變化介于初始速度V0與 最大速度Vm之間，其中V0=[0000]T，Vm=[0.50.50.55]T。假設AUV穩定的作業速度為Vm，在該作業速度附近考慮 2 0%的不確定性，則非線性阻尼系數矩陣Dn(|V|)可轉化為含不確定性的線性矩陣Dnl，即

式中：Pd=diag(0.2,0.2,0.2,0.2);?d=diag(δ5,δ6,δ7,δ8)。其中，Pd為 非線性阻尼矩陣的不確定性邊界，?d為非線性阻尼矩陣的不確定集合。

經線性化后，可得到如下具有不確定性的水動力學模型：

式中：M為水動力學模型的慣性矩陣與附加質量矩陣之和；D為水動力學模型的阻尼矩陣。因M和D均為不確定的量，故可使用標稱值和不確定集合表述如下：

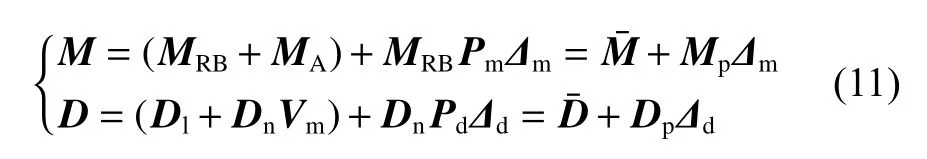
圖1所示為不確定性模型的系統結構。其中，系統輸入為u，對應AUV所受到的外力，即τpro與τenv之 和；系統輸出為y， 對應AUV的位置向量η。如圖1所示，不確定性矩陣包含了M?1和D模塊。本文采用線性分式變換（LFT）方法[20]將不確定性系統變換為廣義系統和不確定集合兩個部分。

圖1 不確定性模型系統結構圖Fig.1 Block diagram of the uncertainty model

其中，模塊M?1和D可以表示為上LFT，即

式中：FU為 上LFT的傳遞函數；Mm為M?1的廣義矩陣；Md為D的廣義矩陣。

對于廣義矩陣P和不確定集合?組成的上LFT，有FU(P,?)=P22+P21?(I?P11?)?1P12，故可得：

上述各公式可用圖2表示，其中um與ym為M?1模塊的攝動輸入和攝動輸出，ud與yd為D的攝動輸入和攝動輸出，wm與zm為M?1模塊的外界輸入與輸出，wd與zd為D模塊的外界輸入與輸出。

圖2 M?1和D的上LFT表示Fig.2 Upper LFT formulation of M?1 andD

綜上所述，對于含不確定集合的系統，可以表示為如圖3所示的結構，其中，u為 4×1的輸入向量，y為 4×1的輸出向量。

圖3 不確定性系統結構圖Fig.3 Block diagram of the uncertainty system

由圖3所示不確定性系統結構圖，選取狀態變量x=[x1x2]T，其中，x1=[xy zψ]T,x2=[uv wr]T，據此，可得到如式（15）所示不確定性系統的狀態空間方程。

消去zd，可得：

由Gcis表示CiscreaAUV四自由度廣義系統，則Gcis有輸入向量[umudu]T和輸出向量[ymydy]T，其狀態空間可表示為：

其中：

從式(17)和式（18）可以看出，廣義系統Gcis不包括不確定性的量，并且Gcis與 不確定集合?共同組成了Ciscrea AUV不確定性模型。如圖4所示，將Ciscrea AUV不確定性模型由上LFT表示為G=FU(Gcis,?)， 其中 ?=diag(?m,?d) 。Gcis的傳遞函數矩陣的奇異值曲線如圖5所示，圖中繪出了Gcis的 4個 奇 異 值 γ1,γ2,γ3,γ4在 頻 域 上 分 布 的 曲線。由圖可見，開環系統最大奇異值是大于1的，不滿足性能約束條件。

圖4 開環模型線性分式變換Fig.4 Linear fraction transformation of the open-loop model

圖5 廣義系統G cis奇異值曲線Fig.5 Singular value curves of the general system Gcis

2 魯棒控制器綜合

圖6所示為考慮不確定性系統一般化跟蹤問題的原理圖。為了方便闡述原理，圖中被控對象為單輸入單輸出系統。其中，r,d,n,e,y,u,yp分別為參考輸入、低頻干擾、測量噪聲、系統誤差、控制輸入、控制輸出和系統測量信號，K為控制器，G為被控對象不確定性模型，它由廣義系統P和不確定集合?組成。將圖6表示為圖7所示的互連系統。圖7中：w為r,d,n組成的外部輸入向量，即w=[r d n]T；z′為設計者定義的性能輸出向量，包括了e,u,yp； 為了表征期望性能，通常會在z′后串聯權重函數矩陣W來評價控制性能，得到評價輸出向量z。

圖6 一般化的跟蹤問題原理圖Fig.6 Block diagram of the general tracking problem

圖7 H ∞魯棒綜合問題的互連系統表示Fig.7 Interconnection system formulation for robust H∞ synthesis problem

考慮閉環系統魯棒穩定性，由小增益定理可知：當?穩 定且 //?//∞＜1時，不確定的閉環系統魯棒穩定性等價于標稱閉環系統WTw→z′(P,K)的內部穩 定 性，且 //WTw→z′(P,K)//∞＜1成 立。由 下LFT的定義可確定傳遞函數Tw→z′(P,K)：

此時，無需考慮不確定性擾動對閉環系統魯棒穩定性的影響，只需考慮標稱閉環系統的性能指標。對于控制系統的跟蹤問題，通常關注e,u,yp等信號，根據這些信號來衡量閉環系統跟蹤能力是否良好、閉環系統響應過程中控制器輸出能量是否合理，以及閉環系統是否抑制干擾等。式（21）表示的則是閉環系統的性能輸出向量z′=[e u yp]T與外部輸入向量w=[rdn]T之間的關系。

通常，采用外部輸入信號到特定性能輸出信號之間的傳遞函數的H∞范數來表征性能指標要求，進而通過優化該范數來優化相應的性能指標。表2所示為具體性能指標。

表2 不同性能指標對應的目標函數Table2 Object functions corresponding to different performance indexes

本文針對Ciscrea AUV的MIMO系統干擾抑制問題對閉環系統性能進行了優化，如圖8所示。參考輸入r和低頻干擾輸入d組成系統的外部輸入向量w， 控制器K、廣義系統Gcis和不確定集合?通過串聯反饋形成閉環系統。權重函數矩陣為W=diag(We,Wu,Wp)（其中，下標p表示yp以示簡潔），通過將其串聯在系統性能輸出向量[eu y]T后得到評價性能輸出ze,zu,zy組成的向量z=[zezuzy]T，其中權重函數We，Wu和Wp分別用來約束閉環系統對特定信號的跟蹤能力、u對外部干擾的抑制能力和y對外部干擾的抑制能力。本文的主要設計目標是抑制外部干擾，系統的性能可以由d到z的H∞范數表示，如式（20）所示。

圖8 閉環系統H∞控制框圖Fig.8 Block diagram of H ∞ control for the closed-loop system

閉環系統的設計目標是在保證閉環系統的魯棒穩定性前提下對性能進行優化，因此，對應的H∞魯棒綜合問題可表示為優化問題，如式（21）所示。

根據上文所述不確定系統跟蹤問題的魯棒穩定性條件，可知：當不確定集合 ?(s)（s表示拉普拉斯變量）穩定且 //?(s)//∞＜1時，閉環系統的魯棒穩定性等價于廣義系統Gcis與 控制器K互連得到的標稱閉環系統的內部穩定性，且 //Td→z(Gcis,K)//∞＜1，亦即

本文在滿足閉環系統魯棒穩定性的前提下，利用經典的ARE方法或LMI方法優化標稱閉環系統性能，即求解 min//Td→z(Gcis,K)//∞。為了降低魯棒控制器的保守性，通常希望優化的目標函數值越小越好。因權重函數是影響優化結果的重要因素，故選取合適的權重函數需要一定的經驗[21]。鑒于r,d均為低頻信號，閉環系統應在低頻的外部輸入信號下具有較小的跟蹤誤差和較強的抗擾性。

因權重函數的逆表征了期望性能，故We,Wp的逆矩陣元素均為高通濾波器。同時，為了最小化控制器的輸出能量并統一量綱，本文選取了合適的權重函數，即Wu=diag(0.01,0.01,0.01,0.01)，并且參考Ciscrea AUV艏搖控制器設計方案，經調試得到了如下權重函數：

圖9 權重函數逆函數幅頻特性曲線Fig.9 Frequency response of the inverse of weighting function

本文利用MATLAB軟件中的LMI工具箱求解最優性能函數值，得到一個20維的MIMO魯棒控制器。圖10所示為閉環系統的奇異值曲線，圖中繪出了標稱閉環系統傳遞函數//Td→z(Gcis,K)//∞的4個奇異值 γ1,γ2,γ3,γ4在頻域上分布的曲線。由圖可見，閉環系統的最大奇異值小于1，則//Td→z(Gcis,K)//∞＜1成立，閉環系統的魯棒穩定性和標稱性能滿足要求。

圖10 閉環系統奇異值曲線Fig.10 Singular value curves of the closed-loop system

3 Ciscrea AUV軌跡跟蹤仿真與分析

為了驗證所提控制系統的有效性，本文對干擾下的定點跟蹤和三維軌跡跟蹤進行了仿真，分別給出了參考輸入r4×1和 干擾輸入d4×1下的標稱閉環系統暫態響應，分別如圖11和圖12所示。

圖11 有參考輸入下的標稱閉環系統暫態響應Fig.11 Transient response of the nominal closed-loop system under reference signal input

圖12 有干擾輸入下標稱閉環系統的暫態響應Fig.12 Transient response of the nominal closed-loop system under disturbance signal input

假設各運動方向的參考輸入r(i)和干擾輸入d(i)均 為分段的階躍信號序列，周期為10 s，r(i)=[2.5311.50]，d(i)=[1.5311.50]，i∈{1,2,3,4}。其中，d(i)可簡單理解為各運動方向位移（角度）的輕微擾動。圖11所示為AUV在橫蕩、縱蕩、垂蕩方向的位置x,y,z和 艏搖方向的歐拉角ψ隨時間變化的曲線。除了計量單位分別是m和 rad以外，各運動方向的參考輸入大小都是一樣的。由圖可見，輸入信號僅含有參考輸入r，并隨時間變化而變化。系統可以快速（調節時間小于5 s）跟蹤參考輸入且無超調，從而驗證了無外部干擾下閉環系統在x,y,z,ψ方向的跟蹤能力。

令參考輸入為0，得到圖12所示的標稱閉環系統在干擾輸入下輸出信號隨時間變化的曲線。由圖可見，干擾輸入下的系統輸出在5s內衰減至0，系統抗擾性得到了驗證。

利用MATLAB軟件模擬Ciscrea AUV在外部干擾下螺旋下沉的場景。真實的風、浪、流通常以力或力矩形式直接作用在AUV上，并對其產生擾動。本文考慮恒定流速與流向的水流對AUV產生的阻尼力。

假設水流流速vd與水平面的夾角為α，在水平面的投影與AUV縱蕩坐標夾角為α1，則水流流速在AUV的x,y,z方向的分量依次為：

水流在固定方向對AUV產生的阻尼力F與流速v的關系表示為

式中：k1,k2分別為二次非線性阻尼系數和線性阻尼系數，各運動方向上的k1,k2值可由阻尼系數矩陣D(|V|)及 水流分量的大小得到。當α=π/6,β=π/3時，通過查表計算，可得流速為 0.3m/s的恒定水流在x,y,z方向產生的水流干擾d=[3.94624.0079 1.8083]TN。

分別在有/無干擾的條件下，令AUV跟蹤空間螺旋曲線s1，同時實現1 rad的艏搖角控制：

式中：參考輸入s1為 空間螺旋曲線，在 50s時加入水流干擾輸入d，在 0～100s時間段內標稱系統的軌跡曲線如圖13～圖15所示。

圖13 有/無干擾下AUV標稱系統軌跡跟蹤曲線對比Fig.13 Comparison of trajectory tracking curves of the AUV nominal system with and without interference

設AUV初始位置為 (x,y,z)=(0,0,0)，初始艏搖角為 0rad，由圖13可見，AUV可以有效跟蹤參考軌跡。由圖14可見，外界干擾并沒有使得系統軌跡嚴重偏離參考軌跡，系統在干擾下仍然保證了其跟蹤精度，這證明了控制系統具有一定的抗擾性。當干擾在ψ方向的分量為0時，由圖15可見，x,y,z方向的干擾作用在AUV耦合數學模型上造成了ψ方向的細微擾動，閉環系統在5s內消除了擾動，其有效性得到了驗證。

圖14 有/無干擾下AUV標稱系統軌跡跟蹤在不同坐標平面投影曲線Fig.14 Trajectory tracking projection curves of the AUV nominal system on different coordinate planes with and without interference

圖15 有/無干擾下AUV艏搖控制暫態響應Fig.15 Transient response of the AUV yawing control with and without interference

為了驗證本文所提控制系統的魯棒性，對不確定性模型G的10個攝動模型進行了閉環系統仿真，結果如圖16所示。慣性矩陣MRB以 [0.3;0.2;0.15;0.1;0.05;?0.05;?0.1;?0.15;?0.2;?0.3]的幅度在標稱模型上變化，得到了被控對象的10個攝動模型。可以看出，圖中的曲線沒有明顯差別，MRB在有界攝動內變化時不會影響系統控制性能。

圖16 有干擾下攝動系統三維軌跡跟蹤曲線Fig.16 Three-dimensional trajectory tracking curves of the AUV perturbation system with interference

本文利用小增益定理保證了閉環系統的魯棒穩定性，在此基礎上求解了 min//Tw→z(Gcis,K)//∞，因此求解的控制器K只能滿足標稱閉環系統的性能條件。本文利用結構奇異值 μ分析方法綜合考慮了魯棒穩定性和魯棒性能。在范數有界的復數不確定性結構擾動下，分別針對閉環系統魯棒穩定性和魯棒性能計算了結構奇異值的邊界。

通過下LFT，將標稱閉環系統表示為M=FL(Gcis,K)， 其中FL為下LFT，則在該系統上施加范數有界的復數不確定性結構集合?得到結構奇異值 μ分析框圖，如圖17所示。圖中，w1與w2均為外部輸入信號，e1與e2為M模塊的輸入和輸出，M對應于不確定性結構?的奇異值定義為

圖17 閉環系統魯棒穩定性分析框圖Fig.17 Robust stability analysis of the feedback system

圖18（a）給出了 μ?(M11jω ）的上、下界及滿足系統魯棒穩定性的 //?//∞的上界，經計算可得γ1=0.24373， 當// ?//∞＜1/0.24373時，不確定的閉環系統均能保持穩定性。圖18（b）給出了μ?(M(jω))的上、下邊界及滿足系統標稱性能的結構奇異值μ，其最大值為0.988 02，而魯棒性能要求下的1 /γ2最高可達1.114 4，即γ2＜1。 對于本文的?=diag(?m,?d)結構，僅當 //?//∞＜1/1.1144時，才能滿足閉環系統的魯棒性能。綜合以上結果，發現在任意復數不確定性結構滿足 //?//∞＜1/1.1144時，閉環控制系統可保證魯棒穩定性并滿足魯棒性能要求。

圖18 閉環系統結構奇異值方法分析Fig.18 Structure singular value analysis of the closed-loop system

4 結 語

本文針對Ciscrea AUV四自由度的非線性不確定性模型設計H∞魯棒控制器，并分析了海流干擾場景中AUV三維軌跡跟蹤性能。結果表明，標稱控制系統可以維持一定的跟蹤精度和響應速度，可有效消除干擾力對AUV產生的輸出擾動，抗擾性能良好。在攝動系統閉環仿真中，AUV未失穩，控制器的魯棒穩定性得以驗證。本文通過結構奇異值分析得到了系統結構奇異值的上、下界，該上、下界保證了控制器的魯棒性能。

AUV的H∞魯棒控制器具有一定的抗擾性，本文求解的是一個四自由度的高階控制器，但因其結構復雜，給實際工程實現帶來了一定的困難。如何求解結構簡潔的MIMO魯棒控制器是未來需要解決的問題。