基于多約束二維排樣的艦載機最大密度布列算法

林信海，楊大鵬，鞏常蘭，李文學(xué)

1 中國艦船研究設(shè)計中心，湖北 武漢 430064

2 華中科技大學(xué) 機械科學(xué)與工程學(xué)院，湖北 武漢430074

0 引 言

艦載機是航空母艦（簡稱“航母”）的主要作戰(zhàn)力量，搭載更多數(shù)量的艦載機對提升母艦作戰(zhàn)效能具有重要意義[1]。考慮到航母甲板空間有限，需在滿足作戰(zhàn)性能要求的前提下，對艦載機開展小型化設(shè)計，并優(yōu)化其外形輪廓，來提高搭載艦載機的數(shù)量和上艦適配性[2]。為量化評估某型艦載機在航母飛行甲板和機庫占地面積的指標(biāo)，美海軍基于近百年的航母艦載機使用經(jīng)驗，提出了“最大密度布列因子”這一指標(biāo)[3-4]。

“最大密度布列因子”簡稱“布列因子”，是可有效表征停放某型艦載機所需占用飛行甲板和機庫空間的一個經(jīng)驗指數(shù)，布列因子越大，表明艦載機占用的航母甲板面積越大。艦載機布列因子的計算流程具體如下[5]：

1） 設(shè)定F/A-18C飛機為基準(zhǔn)艦載機，并規(guī)定其布列因子為1。

2） 按指定規(guī)則和約束，用基準(zhǔn)艦載機填滿“尼米茲”號航母的飛行甲板（不含著艦區(qū)）和機庫，記錄飛行甲板、機庫布列飛機數(shù)量之和，設(shè)其為a。

3） 按同樣規(guī)則布列某型艦載機，記錄布列艦載機的總架數(shù)，假設(shè)為b。

4） 基準(zhǔn)艦載機布列總架數(shù)和某型艦載機布列總架數(shù)的比值，即a/b，就是某型艦載機的布列因子。

艦載機最大密度布列是布列因子計算的核心，目前國內(nèi)外艦載機最大密度布列通常由具有經(jīng)驗的人員借助CAD軟件手工完成，設(shè)計周期冗長且要耗費大量人力，導(dǎo)致艦載機布列因子計算效率低下，因此，急需一種可快速自動生成艦載機最大密度布列方案的算法。

艦載機最大密度布列問題可歸屬于多約束條件下的二維不規(guī)則物體排樣問題[6]。由于二維不規(guī)則物體排樣問題的解空間較大，早期研究人員主要通過拼接和組合方式，將其轉(zhuǎn)化為較易處理的規(guī)則多邊形排樣問題[7-8]，但利用該方法對極不規(guī)則物體進行排樣時，易造成較大浪費。為此，Adamowicz等[9]基于多邊形表示法，提出臨界多邊形（NFP，no fit polygon）算法，通過計算不規(guī)則多邊形的NFP來判定多邊形之間是否干涉。張思[10]采用基于重心NFP算法開展了艦載機自動布列軟件的設(shè)計，但并沒有考慮艦載機最大密度布列時的多個約束條件。

基于上述情況，本文將以二維排樣算法為基礎(chǔ)，重點研究艦載機最大密度布列多個約束條件的數(shù)學(xué)表達、處理策略及基本計算，并分別提出飛行甲板和機庫最大密度布列算法。

1 艦載機最大密度布列約束條件概述

通常來講，與常規(guī)的二維排樣算法相比，艦載機在飛行甲板和機庫最大密度布列要滿足以下約束條件：

1） 距離約束。為滿足布列安全要求，艦載機之間、艦載機與母艦邊界/船體結(jié)構(gòu)之間要保證一定的安全間距。其中，艦載機與母艦邊界/船體結(jié)構(gòu)的距離又包括機與艦外邊界（如甲板邊界、安全停機線）的距離、機與船體結(jié)構(gòu)（如島式上層建筑、機庫壁、機庫防火分隔門等）的距離，根據(jù)艦載機布列轉(zhuǎn)運要求，艦載機之間、艦載機和島式上層建筑等的間距不一樣。

2） 超邊界約束。艦載機身與船體結(jié)構(gòu)、飛行甲板安全停機線應(yīng)保持一定安全間距，不可發(fā)生干涉。但是，在靠近飛行甲板舷邊布列時，在保證艦載機輪與甲板邊緣有一定安全間距的前提下，艦載機機身可超出甲板邊緣，即在布列時需動態(tài)考慮艦載機的外形邊界。

2 艦載機最大密度布列的數(shù)學(xué)表達

2.1 艦載機、飛行甲板和機庫的幾何表達方法

艦載機、飛行甲板和機庫外形輪廓均屬不規(guī)則圖形，其幾何表達涉及到圖形的存儲、判交、平移、旋轉(zhuǎn)等相關(guān)操作，直接影響到布列算法的耗時和精度。目前，主要采用以下方法來表達二維不規(guī)則形狀：原始曲線表達法、多邊形表示法和包絡(luò)法等。本文選用多邊形表示法進行艦載機、飛行甲板和機庫的幾何表達。

多邊形表示法是指采用連通多邊形的形式表達參與布列的甲板和艦載機圖形，若艦載機、甲板輪廓存在曲線邊，則根據(jù)一定的精度將曲線邊近似成直線段來替代，如圖1所示。

圖1 多邊形表示法Fig.1 The polygon-based representation

連通多邊形的定義如下。

定義1：平面連通N邊形P是指N個矢量端點的有序集合。以上矢量端點頭尾相連并按逆時針（順時針）方向排列，且各矢量之間不發(fā)生內(nèi)點相交。

其數(shù)學(xué)表達式為P={P1(X1,Y1),P2(X2,Y2),···,Pi(Xi,Yi),···Pn(XN,YN),i=1···N}。

多邊形表示法降低了圖形之間的操作運算量，提高了排樣速度。雖然在一定程度上會導(dǎo)致不規(guī)則圖形精度的降低，但只要離散精度足夠高，就能夠滿足布列精度需求。

2.2 距離約束數(shù)學(xué)模型及處理策略

如圖2所示，將距離約束劃分如下：l1為艦載機的間距，l2為艦載機和母艦外邊界的間距，l3為艦載機和島式上層建筑等母艦內(nèi)邊界的間距。

圖2 二維排樣中的距離約束Fig.2 The distance constraints of two-dimensional shapes nesting

本文采用等距縮放的策略來處理該距離約束，即對艦載機、甲板的邊界按照一定間距進行放大或者縮小，再開展最大密度布列。設(shè)艦載機的實際間距為l′1，母艦內(nèi)、外邊界的實際間距分別為l′3和l′2，具體見式（1）。之后艦載機以間距l(xiāng)′1將邊界進行放大；甲板以間距l(xiāng)′2將外廓進行等距收縮，以間距l(xiāng)3′將內(nèi)廓進行放大。

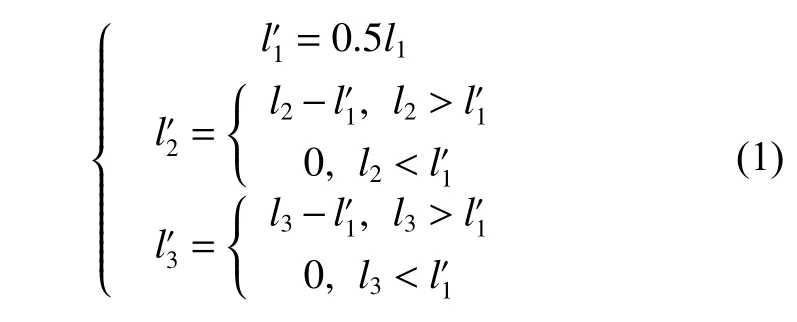
之后，利用分段偏移法對艦載機和母艦進行等距處理，具體流程如下：

步驟1：將艦載機、母艦邊界的每條線段均按等距方向進行等距操作。如圖3所示，線段的起始端分別為Ps(xs,ys)和Pe(xe,ye)， 法向量為n，間距為d。進行等距處理后線段起始點為和，為點Ps到Pe的有向線段，則

圖3 直線的等距計算Fig.3 The offset calculation for lines

步驟2：對等距操作后得到的邊緣進行封閉處理。等距操作后多邊形相鄰兩邊Ci與Ci+1如相交，需對其進行剪裁；如相離，需將其連接至一起，如圖4所示。

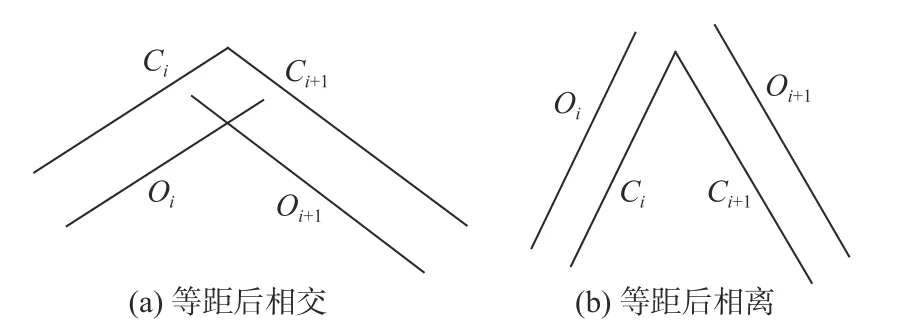
圖4 線段等距后幾何關(guān)系Fig.4 Geometric relation of lines after offsetting operation

本文采用直線延長的方式對相離兩線段進行連接（圖5）。

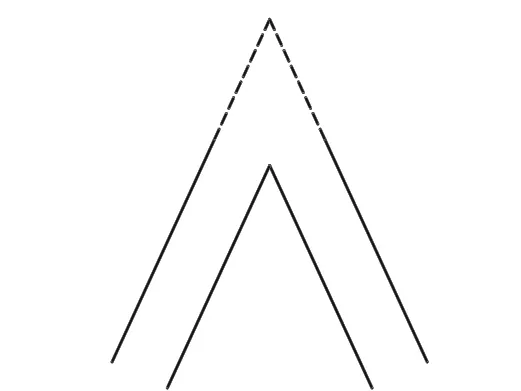
圖5 線段的直線連接方式Fig.5 Connecting operation between lines

步驟3：對生成的原始等距邊界進行檢查，刪除無效的邊界，獲得最終有效邊界。

2.3 超邊界約束數(shù)學(xué)模型及處理策略

飛行甲板上排樣存在超邊界的約束條件，二維超邊界排樣問題可表述為：一組二維不規(guī)則外形的零件P1,P2,···,Pn， 每個零件包含特征點{D1,D2,···,Dm}。需基于以下約束條件，在樣板P中以最大密度排放以上零件P1,P2,···,Pn，需滿足：

1） 任一零件Pi，Pj互不干涉。

2） 零件Pi的特征點{D1,D2,···,Dm}與樣板P的外邊界保持一定間距。

圖6是艦載機超邊界擺放的情況，即艦載機的機身邊界可以超出飛行甲板停放，只要艦載機的機輪（通常為1個前輪和2個主輪）等特征點未超出飛行甲板邊界即可。

圖6 艦載機超邊界布列方案Fig.6 Aircraft spotting plan under the constraint of overlapping the boundary

傳統(tǒng)的排樣算法無法滿足超邊界排樣計算需求。考慮到可將樣板分為飛行甲板邊緣處的超邊界排樣區(qū)域和甲板內(nèi)的常規(guī)排樣問題，可采用不同的算法對其按先后次序進行計算。如先排布甲板邊緣、再排布甲板內(nèi)部，則為外圍收縮次序；如先排布甲板內(nèi)部，再排布外板，則為中心膨脹次序（圖7）。

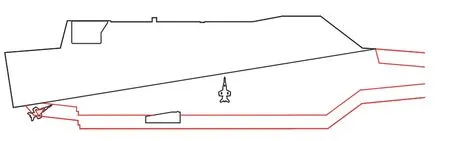
圖7 甲板不同區(qū)域情況Fig.7 The different regions of flight deck

本文采用的外圍收縮排樣順序可概括為：在飛機機輪不超出甲板邊界的前提下，將飛機盡可能多地向甲板邊緣和最小重心點移動，依次將飛行甲板外邊界布滿飛機，再開始對甲板內(nèi)部區(qū)域進行飛機排布。

綜上所述，超邊界布列的定位步驟為：

1） 利用某圖形格式導(dǎo)入飛機和飛行甲板的外形邊界信息，在飛機圖形中以不同圖層標(biāo)識飛機的特征點。

2） 獲取飛機的特征點，根據(jù)特征點是否超出甲板區(qū)域，判定飛機是否越過邊界。

3） 基于外圍收縮順序進行排樣，即先進行飛行甲板邊緣的飛機布列，再進行甲板內(nèi)部區(qū)域的飛機布列。

3 機庫艦載機排樣算法

艦載機在機庫內(nèi)的最大密度布列可視為非等距約束下的不規(guī)則物體二維排樣算法，其優(yōu)化目標(biāo)就是使機庫內(nèi)艦載機數(shù)量最大化。本文擬基于最低重心NFP算法[11]對其進行處理，機庫最大密度布列算法流程圖如圖8所示。

圖8 機庫最大密度布列流程圖Fig.8 The workflow of maximum density spotting plan on the hangar deck

機庫最大密度布列算法的步驟為：

1） 利用.dxf格式導(dǎo)入飛機和機庫外形邊界信息，并利用多邊形表示法將其轉(zhuǎn)化為離散點。

2） 根據(jù)最大密度布列準(zhǔn)則要求，分別輸入飛機之間，飛機與機庫防護分隔門、機庫壁的間距。

3） 基于式（1）和式（2），利用擴展等效策略處理艦載機和機庫邊界。

4） 利用最低重心NFP算法布列艦載機。最低重心NFP算法的排樣規(guī)則將飛機放在重心最低的位置。其出發(fā)點是在不產(chǎn)生干涉的前提下，使布列艦載機的重心最低，為后面布列的艦載機留出更多的布列空間。其步驟為根據(jù)飛機外形邊界得出其重心；然后以指定的角度間隔（本文為1°）旋轉(zhuǎn)飛機，求解各旋轉(zhuǎn)角度下的重心NFP，記錄最低重心位置及對應(yīng)的旋轉(zhuǎn)角度，對飛機進行定位。采用最低重心NFP方法，獲得最低重心的示意圖（圖9）。

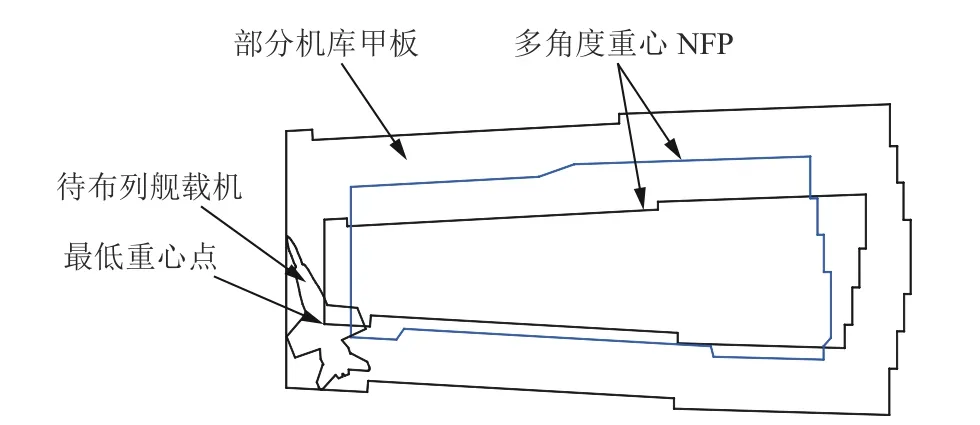
圖9 最低重心NFP算法Fig.9 Lowest-gravity-center NFP algorithm

5） 從機庫甲板上除去已布列飛機的面積，獲得新的機庫輪廓（圖10），再進行下一步布列。

圖10 新機庫邊界的合成Fig.10 Regeneration of the hanger deck contour

6） 重復(fù)以上步驟，直至剩余的機庫空間不足以容納1架飛機為止。

4 飛行甲板艦載機排樣算法

針對飛行甲板艦載機最大密度布列，本文基于外圍收縮順序[12]，分別對飛行甲板邊緣和內(nèi)部依次按最大密度排布的方式進行計算。首先利用啟發(fā)式靠邊定位算法對甲板邊緣處的飛機進行布列，直到飛行甲板邊緣無法超邊界布列飛機；然后采用機庫最大密度布列飛機的NFP算法，對飛行甲板內(nèi)部的飛機進行排樣，直到甲板內(nèi)布滿飛機。飛行甲板艦載機排樣的算法流程如圖11所示。

圖11 超邊界約束下的艦載機布列算法流程圖Fig.11 The algorithm workflow for aircraft spotting under the constraint of overlapping the boundary

啟發(fā)式靠邊定位算法的主要思想為：對于邊L1（圖12），將甲板的最左最下位置作為“零件局部最優(yōu)”位置，沿L1的反方向采用該定位策略逐一布列艦載機，直至沿該方向無法布列艦載機為止；之后先后沿L2～L4的反方向采用類似的方式放置剩下的艦載機，只不過它們的“零件局部最優(yōu)位置”則分別更新為最右最下位置、最右最上位置、最左最上位置，最終完成甲板邊緣所有艦載機的布列。

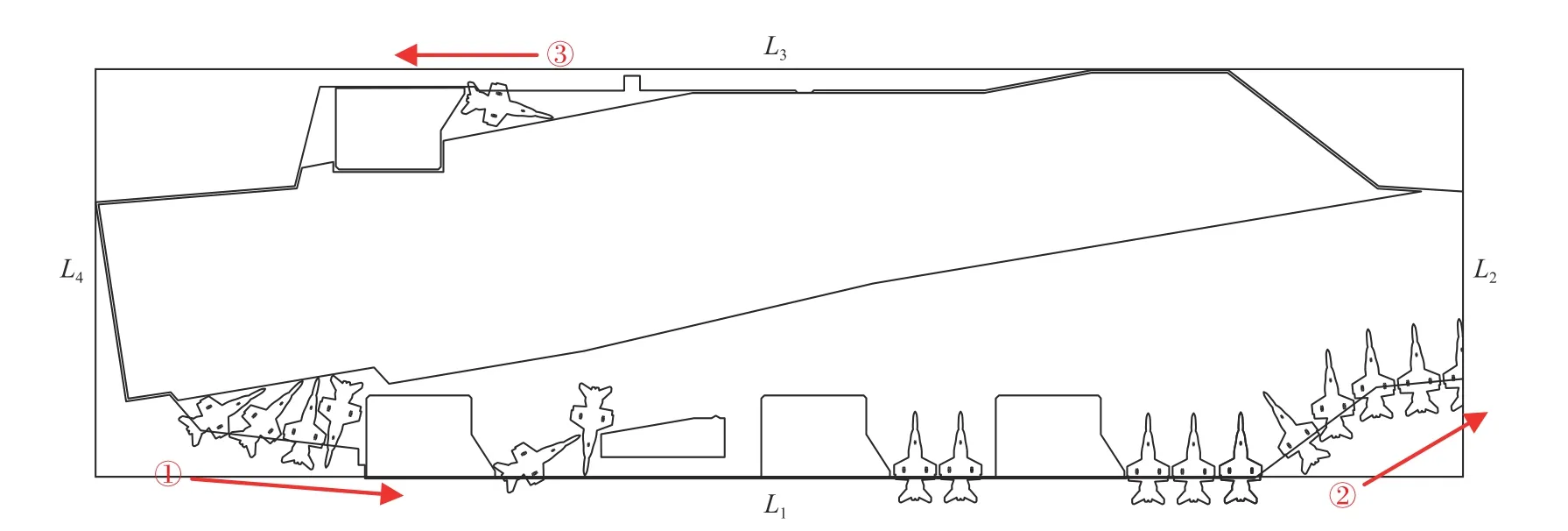
圖12 啟發(fā)式靠邊定位算法流程圖Fig.12 The workflow of heuristic algorithm for keep-to-the-boundary spotting

基于該算法的飛行甲板邊緣艦載機最大密度布列的具體步驟如下（圖12）：

1） 以飛行甲板的艉部最右側(cè)為起點，沿著右側(cè)甲板邊緣，按自艉向艏的方向，基于最艉最右位置為“零件局部最優(yōu)”位置為原則開始布放飛機，直到該方向無法布列飛機。

2） 沿著艏部、左舷等甲板邊緣，分別基于最艏最右、最艏最左位置為“零件局部最優(yōu)”位置，完成飛行甲板邊緣艦載機的布列。

5 算法實驗結(jié)果

利用上述算法對F/A-18C飛機進行最大密度布列（圖13），其中飛行甲板和機庫的外形尺寸及邊界根據(jù)文獻[13]確定，飛行甲板和機庫分別布列了76架和53架，總計129架飛機，與美軍公布的飛行甲板和機庫可最大密度布列130架F/A-18C飛機[14]基本吻合。

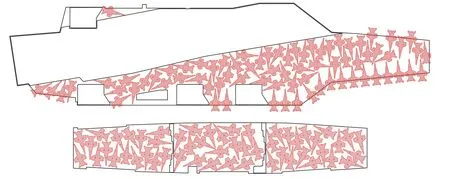
圖13 F/A-18C飛機在飛行甲板和機庫的最大布列圖Fig.13 Maximum spotting pattern of the F/A-18C aircraft on the flight and hangar deck

以F/A-18C飛機為基準(zhǔn)艦載機，對F-35C飛機進行最大密度布列（圖14），飛行甲板和機庫分別布列了69架和46架機，即可最大布列115架F-35C飛機，根據(jù)定義，其布列因子為1.12，與美軍公布的F-35C飛機布列因子[4]為1.11基本相當(dāng)。

圖14 F-35C飛機在飛行甲板和機庫的最大布列圖Fig.14 Maximum spotting pattern of the F-35C aircraft on the flight and hangar deck

6 結(jié) 語

本文以最低重心NFP算法為基礎(chǔ)，針對艦載機最大密度布列的距離和超邊界約束進行分析，提出了距離約束的數(shù)學(xué)模型及處理策略，以及利用啟發(fā)式靠邊定位算法來處理超邊界約束，并基于飛行甲板和機庫艦載機布列具體約束，分別提出了飛行甲板和機庫最大密度布列的算法。利用該算法得到“尼米茲”航母可最大密度布列129架F/A-18C或115架F-35C飛機，以及F-35C飛機布列因子為1.12等有意義的結(jié)論，與美軍相關(guān)文獻公布的艦載機布列數(shù)據(jù)基本吻合，證明了算法的實用性。