不同外形聲吶的水動力及流噪聲數值模擬分析

2022-01-14 01:39:58鄧云傅何琪廣超越陳威林永水

中國艦船研究 2021年6期

鄧云，傅何琪，廣超越，陳威*，林永水

1 武漢理工大學理學院，湖北武漢 430063

2 中國船舶及海洋工程設計研究院，上海 200011

0 引言

拖曳式線列陣聲吶的主要作用是利用聲波在海洋中傳播能量衰減的能力弱且能遠距離傳送等特點，對目標進行定位、警戒等。拖曳式聲吶由水聽器和護套2個部分組成，當聲吶工作時，聲吶與海水間的相對運動會產生湍流邊界層，引起壓力起伏，產生流噪聲。近年來，拖曳式列陣聲吶的流噪聲問題受到了研究者們的廣泛關注[1-2]。

研究發現，聲吶外形很大程度上會影響水動力及流噪聲性能，故學者們從2個方面展開了一些研究。在水動力數值研究方面，張曉峰等[3]以三維剛性圓柱為研究對象，探討了不同雷諾數、間距比和排列方式下單、雙圓柱的水動力特性，研究結果為圓形聲吶流場特性的精確預報提供了一定的指導。王建春等[4]分析方柱繞流的復雜渦系結構，為研究方形聲吶外輻射奠定了理論基礎。彭華康等[5]運用統計能量法建立了水下橢球殼外形的聲吶腔模型，考慮在橢球聲吶湍流脈動壓力空間分布不均勻的條件下計算得到不同航速時聲吶罩表面湍流邊界層的分離點，可為水下橢圓形聲吶自噪聲預報和控制提供參考。

在流噪聲數值研究方面，Sung等[6-8]分析了聲吶內部不同外形的水聽器對降噪的影響，發現矩形和圓形的降噪效果優于菱形和三角形。湯渭霖等[9]研究了流噪聲產生的機理，指出流噪聲的強度大小與水聽器結構設計存在著很大的關系。王曉林等[10]從擴大水聽器和護套表面距離以及結構減振優化的角度提出了拖曳聲吶流噪聲的抑制方法。劉明星等[11]對不同聲吶基陣類型的水動力噪聲進行仿真分析，得到了球陣水動力噪聲要小于圓柱陣水動力噪聲的結果。由于目前的研究一般是通過設計聲吶內部的水聽器外形來降低流噪聲在聲吶內部的耦合效應，因此在降低聲吶護套外部的湍流邊界層壓力起伏引起的流噪聲研究方面則顯得不足。因此，有必要從抑制流噪聲的角度對聲吶護套外形進行合理的聲學設計。

然而，開展聲吶流噪聲的相關研究需從不同聲吶外形的角度對其流場和聲場進行分析，以得到不同外形聲吶的聲場和流場分布規律，這不僅在聲吶結構設計方面具有重要的研究價值，在提高聲吶工作性能方面也具有重要的實用價值。

鑒此，為降低傳統圓形聲吶外表面流噪聲，本文設計了3種不同外形（圓形、方形、橢圓形）的聲吶，擬通過對比聲吶外表面的流場和聲場分布規律，降低傳統的圓形聲吶外表面流噪聲，合理優化聲吶的設計。

1 數學模型以及網格系統

1.1 流場理論

研究過程中，描述流場的無量綱數主要包括雷諾數Re、阻力系數CD、升力系數CL、斯特勞哈爾數St。斯特勞哈爾數等于當地慣性力與遷移慣性力之比，而雷諾數等于慣性力與黏性力之比。具體定義式如下：

式中：fv為渦脫落頻率；D為圓柱直徑；U為來流速度；υ為流體動力黏度。

升力系數CL和阻力系數CD定義式如下：

式中：FD為圓柱所受到的阻力；FL為圓柱受到的升力；ρ為流體密度；A為圓柱的迎流面積，在二維情況下為圓柱的直徑。

1.2 聲場理論

在進行近場流場計算后，取聲吶周圍為聲源，得到近場強度大小和分布規律，并將聲場相關的量傳至遠場。在整個傳遞過程中忽略流動和波動對聲場的影響，龍雙麗等[12]使用基于FW-H方程[13-14]的積分外推方法計算出了外流場的聲學信息，如式(5)所示。FW-H方程的右邊3項代表聲輻射源，其中，第1項代表流體本身的湍流應力，具有四極子特性；第2項代表施加在某些界面上非穩定力的散度，具有偶極子特性；第3項代表進入到流體中的非穩定質量流，具有單極子特性[15]。由于聲場計算過程中時間具有滯后性，會造成聲場結果的不可靠性，因此，為得到準確聲場信息，應在穩定的流場中進行聲場計算。

式中：nj為控制面上的單位外法向矢量；ui為xi方向的速度分量；un為流體在f=0面上的法向速度；vn為物面速度方向的法向分量；ρ0為流體密度參考值； ω(f)為 Dirichlet 函數；H(f)為Heaviside廣義函數；?2為拉普拉斯算子；p′為遠場聲壓；a0為遠場的聲速；Tij為Lighthill應力張量；Pij為可壓縮流體應力張量。

1.3 計算模型和流域參數

本文主要研究二維情況下不同外形的聲吶表面水動力及流噪聲的分布規律。建模過程從幾何建模、設置物理參數、邊界條件以及求解方式等幾個方面來進行。圓形聲吶建模過程是以坐標原點為圓心，圓心距離上、下邊界分別為1 0D，距離左、右邊界分別為1 0D和 25D，建模過程取圓柱直徑D=10 mm，方形聲吶建模將其中的圓形變為方形即可。橢圓的流場特性與橢圓的長、短軸的比值有關，為了研究方便，取長、短軸比值為2:1，即a=2D，b=D，圖1所示為計算域。

圖1 不同外形的聲吶計算域圖Fig.1 Computational domain of sonar with different shapes

模擬中，流體介質為水，其密度為998.2 k g/m3，運動黏度為 1 .004×10?6m2/s2，本文雷諾數取為3 900，該雷諾數下流動狀態為湍流[16]，湍流模型選擇標準k?ε模型。相較于其他湍流模型，湍流k?ε模型具有穩定性、經濟性和比較高的計算精度等優點[17]。左側邊界為速度入口，右側邊界為出口邊界，上、下邊界為對稱邊界，內部圓柱為無滑移靜止壁面。為加快求解的收斂，本文選擇了SIMPLEC壓力速度耦合方式，相比SIMPLE方法，SIMPLEC方法在四邊形網格上收斂性更好。

1.4 網格和時間步驗證

為驗證計算結果的合理性，以圓形聲吶流場模型為例，對不同網格密度和時間步長的組合進行驗證[16,18]，計算參數和結果如表1所示。表中，?x為圓柱周圍最小的網格尺寸，?t為時間步長，為平均阻力系數。

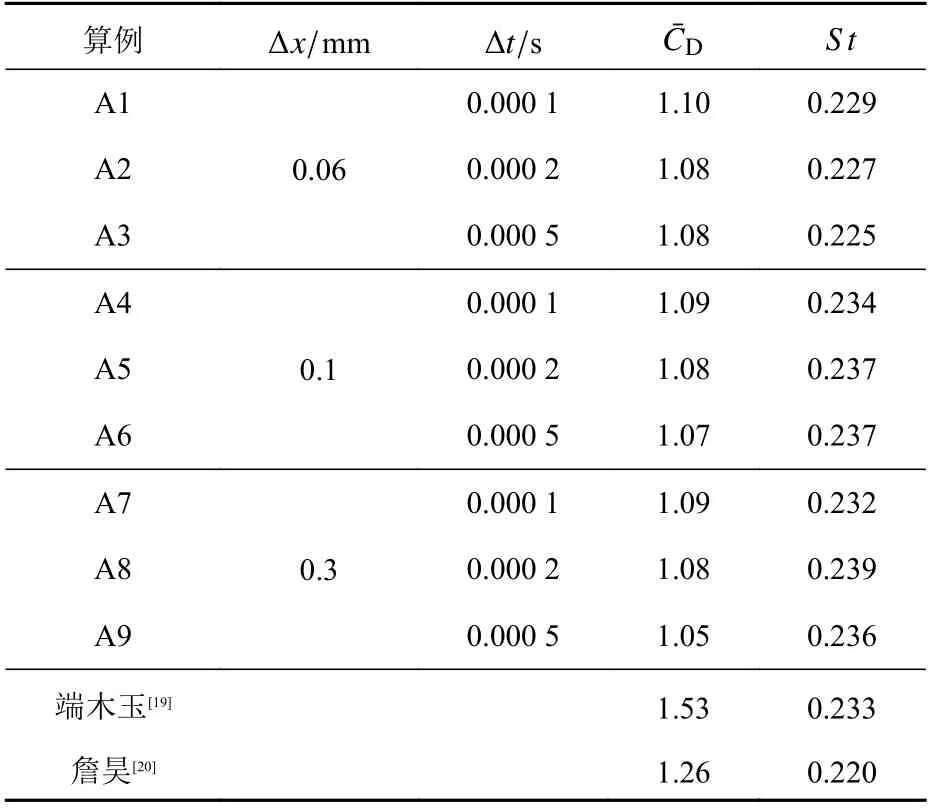
表1 R e=3900的圓柱繞流計算結果和參數Table1 Calculation results and parameters of flow around cylinder at Re=3900

由表1可見，3種網格計算出的CˉD均能夠較好地滿足數值計算結果的要求。從計算效率的角度而言，網格尺寸過小會造成計算效率偏低，故計算時采用了相對較大的0.3 mm網格尺寸。在確定網格尺寸之后，根據Courant數選擇合適的時間步長。Courant數定義如下：

Courant數為在一個時間步長內一個流體質點可以穿過的網格數。若選擇的時間步長合理，則Conrant需小于1，才能確保計算的精度。若選擇中等長度的時間步長0.000 2 s，則Courant數為0.26。此時，結果與文獻[19-20]比較吻合，表明結果及建立的模型是有效的。因此，所有模型均選擇A8算例進行水動力及流噪聲的分析。

2 結果分析

2.1 流場及水動力結果分析

分析3種不同外形的聲吶阻力、升力系數，結果如圖2所示。隨著時間的推移，圓形聲吶CL振幅逐漸增加，CD均值先增后減，然后緩慢增加到穩定狀態，最后呈現出CL幅值在0.85、CD均值在1.08的周期性單一頻率振動。而方形的水動力系數較大，CL幅值為1.31，CD均值為1.80。與圓形和方形外形的聲吶相比，橢圓形的聲吶水動力系數都較小，CL幅值為0.05，CD均值為0.43。

圖2 不同外形聲吶升阻力系數Fig.2 Lift and drag coefficients of sonar with different shapes

圖3所示為3種外形聲吶的升力頻譜特性曲線。其中：圓形的升力頻率（渦脫落頻率）為9.26 Hz，其斯特勞哈爾數為0.236；方形的升力頻率（渦脫落頻率）為5.82 Hz，其斯特勞哈爾數為0.148；橢圓形的升力頻率（渦脫落頻率）為10.80 Hz，其斯特勞哈爾數為0.275。通過比較，發現方形聲吶的斯特勞哈爾數最小，橢圓形聲吶的斯特勞哈爾數最大。這說明方形渦旋脫落周期較長，橢圓的渦旋脫落周期較短。

圖3 不同外形聲吶頻譜Fig.3 Spectrum diagram of sonar with different shapes

圖4所示為3種外形聲吶的渦量圖。聲吶周圍表面的渦旋脫落會引起表面壓強的周期性變化，使升力和阻力周期性變化，且因正、負渦交替脫落的渦強度相等，造成升力系數均值為0。水平端前、后兩側受到的壓力方向一致，造成阻力系數均值不為0[21]，由圖4可見，在相同計算域內，圓形與橢圓外形的聲吶存在4對脫落渦旋，方形存在2對脫落渦旋，說明在圓形與橢圓外形下渦脫落頻率相差不大，但與方形渦脫落頻率相比，相差較大，約為方形渦脫落頻率的2倍。可見，渦脫的差異造成了升力頻率不一。另外，方形邊界層分離位置在方形的前端上、下兩個角點位置，而圓形邊界層分離的位置則在中間且稍偏后的位置，橢圓形的分離位置相比圓形，位置更靠后一些，且邊界層拉長造成的尾渦長度大于圓形。可見，分離點的差異造成了壓差阻力的不同。因此，相比較而言，方形聲吶的阻力系數最大，橢圓形的最小。

圖4 不同外形聲吶的渦量圖Fig.4 Vorticity picture of sonar with different shapes

2.2 聲場及流噪聲分析

在圓形外形的聲吶周圍定義6個測點，位置分別為1（0，0），2（D，0），3（?D，0），4（0，D），5（0，?D），6（10D, 0）。其中，2和3號測點的位置是關于垂直軸對稱，4和5號測點是關于水平軸對稱。測點的具體位置如圖5所示。方形和橢圓外形的聲吶周圍測點的位置與圓形的相同。

圖5 圓形聲吶監測點的定義圖Fig.5 Definition diagram of monitoring points for circular sonar

圖6所示為3種不同外形聲吶的聲壓頻譜曲線。各測點聲壓最大值所對應的頻率為渦脫落頻率，且各聲壓峰值處的頻率均為渦脫落頻率的整數倍。測點6距離聲吶距離最遠，其聲壓值最小。如表2所示，3種聲吶的總聲壓級中，橢圓形聲吶的內、外部總聲壓級最小；距離聲吶中心最遠測點處總聲壓級最小，距中心相同的平行來流方向測點（測點2和3）、垂直來流方向測點（測點4和5）處總聲壓級差別不大。對比3種不同外形聲吶，圓形的總聲壓級在內部的測點最大。

圖6 不同外形聲吶的聲壓頻譜曲線Fig.6 Sound pressure picture of sonar with different shapes

表2 各測點對應的總聲壓Table2 The total sound pressure corresponding to each measuring point

圖7所示為3種外形的聲吶外輻射指向特性圖。由圖可見，各外形聲吶外輻射指向都呈現出一個“8”字形，說明流噪聲的主要來源為表面交替渦脫落產生的非定常脈動力形成的偶極子聲源。其中，圓形和方形聲吶的外輻射特性規律類似，都呈現出“正8字”形的偶極子聲源特性，與李玲等[22]給出的結果相似，即聲輻射橫向最大、水平來流方向最小。這是因為橫向聲輻射主要源于渦脫落產生的非定常脈動力，而水平來流方向主要源于渦脫落中湍流應力，從圖3中也可以看出，圓形和方形聲吶的橫向的升力幅值較大。此外，從表2也可以發現，等距的橫向測點4和5的總聲壓級要大于水平測點2和3的總聲壓級。與圓形和方形聲吶不同，橢圓形聲吶外輻射特性呈現出“倒8字”形，聲場外輻射的最大值發生在水平來流方向，而與來流方向成70°，外輻射值最小，對應的升力幅值也較小（見圖2），且等距的水平測點2和3的總聲壓級要大于橫向測點4和5的總聲壓級(見表2)。