高壓高產氣井完井管柱振動特性及安全分析*
康志磊 郭 蒲 文小勇 姚 霖 張鵬翔 王海軍
(1.中石化西南石油工程有限公司測井分公司 2.中國石油集團長慶油田分公司第一采油廠3.中國石油集團川慶鉆探工程有限公司川西鉆探公司 4.中國石油集團西南油氣田分公司勘探事業部5.中國石油集團西部鉆探工程有限公司吐哈鉆井公司)
0 引 言
完井管柱是連接地層與地面的重要通道,在油氣井生產過程中由于高速流體流經管柱,誘發管柱振動,而管柱振動又會影響流體流態變化,進而形成流固耦合振動。振動會造成管柱在低應力狀態下的疲勞破壞,降低接箍螺紋的密封性能,甚至造成完井管柱斷裂失效事故。因此,研究完井管柱振動對確保管柱安全具有重要意義。
近年來,許多學者對管柱流固耦合振動規律進行了研究。W.BURMANN[1]擴展了經典的水錘模型,建立了直管流固耦合的軸向振動四方程模型,研究了管柱系統不同流段的“水擊”現象。C.SEMLER等[2]考慮管柱兩端固定支承條件下縱向張力和橫向撓度引起的大曲率的影響,建立了充液管的非線性運動微分方程。楊超[3]研究了非定常流直管與彎管耦合振動特性及響應計算方法,分析了阻尼和軸承邊界條件對系統振動的影響。B.SREEJITH等[4]考慮流體與管柱系統相互作用影響,建立了耦合動力方程有限元模型,其研究結果表明,考慮流固耦合響應的充液管道,在閥門關閉等流體瞬態激勵下的結構速度明顯降低。A.S.TIJSSELING[5]建立了充液管道軸向振動中流體與管柱相互作用的一維方程,提出了流固耦合波速度的計算方法,得出薄壁假設對較厚管柱的長波有效,而液體摩擦效應和結構阻尼效應較小的結論。李子豐等[6]研究了流體黏度對鉆柱縱向振動的影響,得到了鉆井流體的黏度越小,鉆柱的振動幅度越大的結論。樊洪海等[7]研究了氣井管柱的流固耦合振動四方程模型,研究結果表明,天然氣的瞬變流動通過泊松耦合效應誘發完井管柱軸向往復運動,加劇了完井管柱結構的疲勞破壞與磨損破壞。高寶奎等[8]研究了高溫高壓井中測試管柱變形的增量,屈曲后的油管進一步變形時,油管軸向力與變形的關系較復雜,提出用塑性力學增量理論的方法進行計算。練章華等[9]建立了完井管柱臨界屈曲載荷數學模型,分析了井口油壓、產量和管柱屈曲對管柱振動的影響。曹銀萍等[10]運用ANSYS軟件建立了油氣井管柱有限元模型,得出考慮流固耦合作用時管柱的固有頻率小于無流固耦合時的固有頻率的結論。丁建東等[11]開展了儲氣庫注采管柱振動模擬試驗,得到了氣體流速、管柱直徑及管柱軸向力等條件下管柱的振動規律。
盡管學者們對管柱流固耦合開展了較多的研究,但針對完井管柱氣體誘發管柱振動的流固耦合問題分析還是較少。為此,本文建立了完井管柱流固耦合模型,編制了Fortran程序,并結合華北油田某井現場數據模擬完井管柱的流固耦合振動過程,針對完井管柱的振動特性進行分析,以期為完井管柱能夠安全生產提供借鑒。
1 完井管柱流固耦合振動模型
高壓高產氣井完井管柱是油氣等底層流體產出和地面工作液注入產層的通道,管柱系統主要由油管、安全閥、伸縮節、滑套、封隔器及射孔槍等部件組成,其簡化結構如圖1所示。
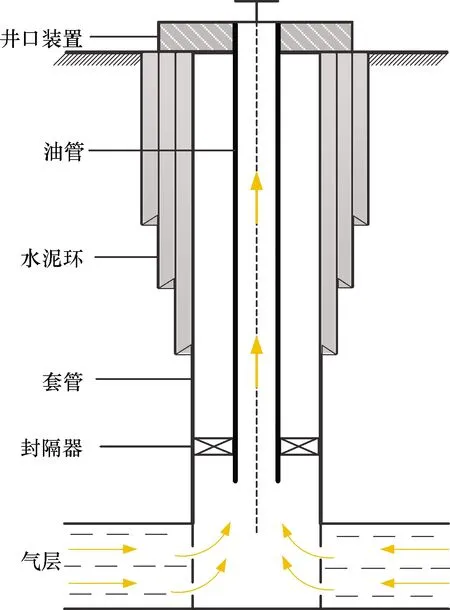
圖1 高產高壓氣井完井管柱系統簡化圖
氣體在管柱內向上流動的過程中,由于氣體具有一定的流速和壓力,使得管柱振動進而產生變形,而管柱振動產生的變形又會影響氣體的速度和壓力分布,氣體與管柱之間相互影響,相互作用,進而形成了氣體與完井管柱之間的流固耦合作用問題。
1.1 假設條件
對完井管柱進行流固耦合分析時,做如下基本假設:
(1)管柱是一個等截面、純彈性、小形變、薄壁且各向同性的圓管柱;
(2)氣體為均質氣體,氣體在管柱內做簡單恒定流運動;
(3)忽略管柱結構阻尼與流體內部阻尼。
1.2 模型建立
針對氣體誘發完井管柱系統流固耦合振動的研究,采用的流固耦合模型是一組雙曲線偏微分方程。該模型的控制方程包括氣體狀態方程、連續方程、氣體與管柱的軸向和徑向運動方程、管柱的幾何與物理方程以及氣體與管柱接觸面處的動力、運動耦合邊界條件。模型由4個方程構成,分別由兩個氣體方程與兩個管柱方程相互耦合。該模型體現了氣體與管柱之間的泊松耦合與摩擦耦合[12]。
流體運動方程:
(1)
流體連續性方程:
(2)
管柱運動方程:
(3)
管柱應力與位移關系方程:
(4)
式中:p是氣體壓力,Pa;v是氣體流速,m/s;ρf是氣體密度,kg/m3;ρp是管柱密度,kg/m3;E是管柱彈性模量,Pa;e是管柱壁厚,m;R是管柱半徑,m;uz是管柱的速度,m/s;σz是管柱的應力,Pa;γ是管柱泊松比;K是氣體體積模量,Pa;λf是氣體摩阻系數;λw是管柱與套管的環形空間中充填完井液的摩阻系數。
1.3 模型邊界條件
完井管柱系統流固耦合時域分析是在定解條件下求解管柱流固耦合方程組的數值解,因此,在對管柱進行動力響應計算時,應建立管柱初始狀態和定解條件。打開井口閥門時的上端邊界條件為上端點的位移z=0,于是有閥門孔口方程:
(5)
式中:(v-uz)o、Δpo分別是穩定流動時氣體的相對速度及壓降,τ(t)是時間函數。
對于井底壓力維持常壓,下端點的位移z=L,于是有:
σz|z=L=(p|z=L-p|z=0)
(6)
1.4 模型求解
式(1)~式(4)為擬線性雙曲線偏微分方程,本文采用特征線法來求解雙曲線偏微分方程。特征線法的主要思路是將偏微分方程轉化為常微分方程,即特征方程,從而轉化為有限差分方程求得近似解。在求解過程中,首先將管柱系統劃分為若干計算單元。由于特征線與空間坐標軸無法相交于網格點,需要對管柱的空間步長Δz和時間步長Δt做一定的規定。根據管柱系統的結構特點,管柱計算單元的長度可能不相同,另外流體沿著特征線傳播的波速λ也不相等,因此,為了保證計算格式的穩定,需要滿足式(7)。
(7)
式中:Δzmin是管柱所有計算單元最小的長度,λmax是流體傳播最大的波速。
該模型的求解流程如圖2所示。
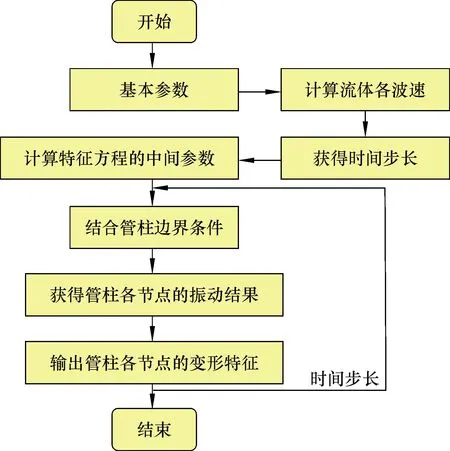
圖2 模型求解流程
2 現場應用及算例分析
2.1 基本數據
選取華北油田某井[9,13]為對象,研究完井管柱的振動特性。利用本文建立的完井管柱流固耦合模型,可以對完井管柱產氣過程中管柱的振動特性進行模擬,研究產氣量、井口壓力和氣體密度等參數對完井管柱振動的影響。計算時完井管柱的基本參數如下:井深4 258 m,套管直徑177.8 mm,管柱外徑88.9 mm,管柱內徑76.0 mm,封隔器位于井下4 185 m處,管柱密度7 850 kg/m3,管柱彈性模量210 GPa,管柱泊松比0.3,地層壓力48 MPa,井底流壓42 MPa,井口壓力25 MPa,產氣量60×104m3/d,氣體密度取220 kg/m3,氣體體積模量取10 MPa。
圖3為管柱橫向位移隨時間的動態變化圖。從圖3可以看出,當氣體流經完井管柱時,管柱會發生劇烈的振動,之后會逐漸減弱。
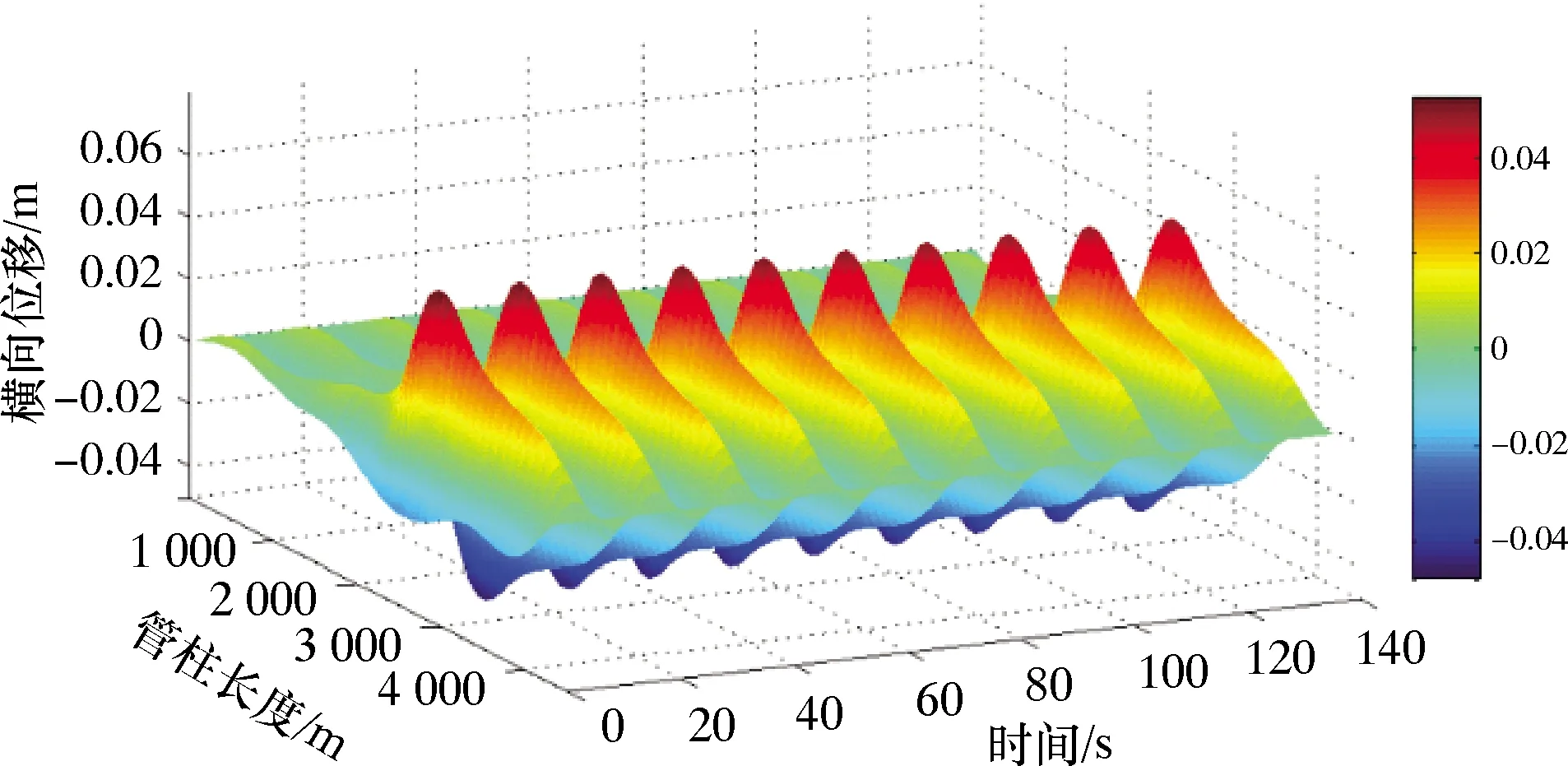
圖3 管柱橫向位移隨時間的動態變化圖
圖4為管柱在t=5、10、15和20 s時的橫向變形圖。管柱從頂部到底部的橫向變形逐漸增大,此后逐漸減小。管柱在2 980和3 832 m處存在較大的變形。從圖3和圖4可以看出,管柱在開井瞬間產生的振幅較大,而后振動呈現逐漸衰減的趨勢。在振動衰減的過程中,管柱的最大橫向變形出現在管柱的中下部位置。這是因為在閥門開啟瞬間,高壓氣體通過完井管柱,使得管柱內的壓力突然升高,壓力升高會引起氣體對管柱內壁作用力的增大,使得管柱產生較大的振動。隨著氣體壓力的逐漸穩定,氣體對管柱內壁作用力減小。另外,管柱的剛度使其具有抵抗橫向變形的能力,整個管柱振動逐漸減弱[3]。在完井管柱的上、下端固定約束時,完井管柱的中下部剛度相對較小,易發生橫向振動,管柱易發生破壞。
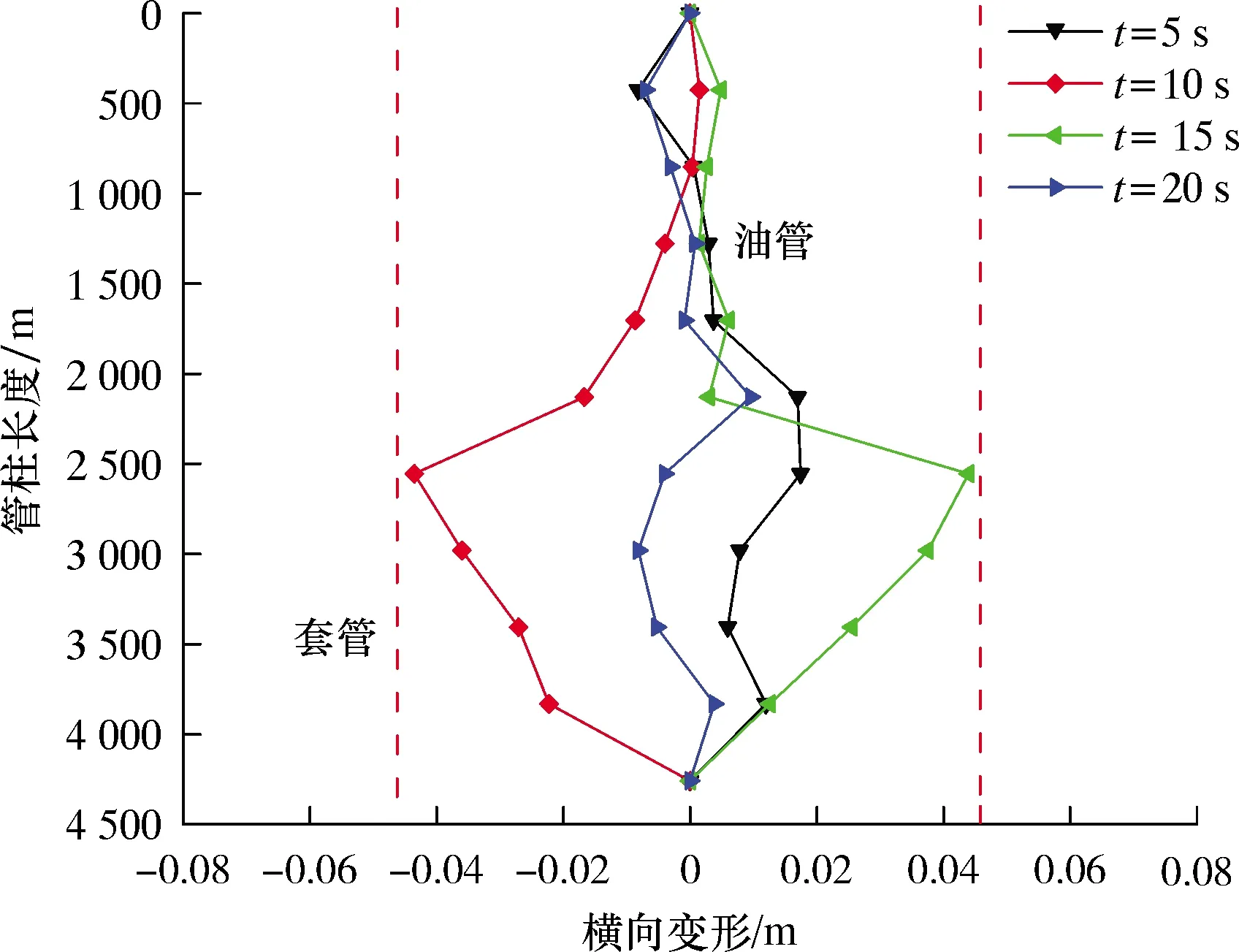
圖4 不同時刻管柱橫向變形圖
2.2 產氣量對完井管柱振動特性的影響
圖5為不同產氣量Q下管柱在5、10、15和20 s時的橫向變形圖。從圖5可以看出,完井管柱的橫向變形隨著產氣量的增加而增大。這是因為管柱內氣體產量增大時,氣體流速升高,氣體對管柱的沖擊力增大,使得管柱的變形增大;另外,隨著氣體產量的增加,氣體的壓能增加,氣體與管柱之間的耦合作用加劇,氣體的壓能轉化成管壁的振動能量,管柱的變形增大[3]。
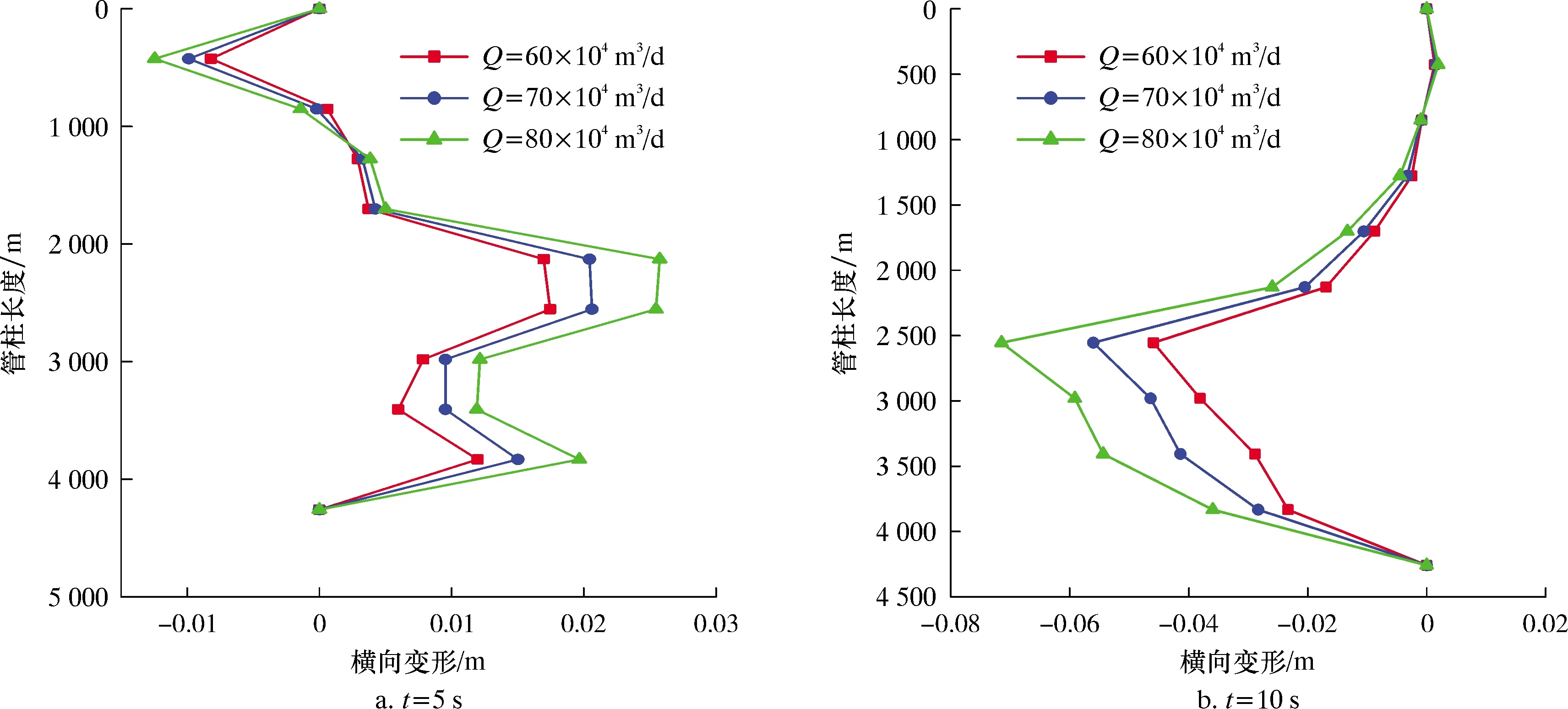
圖5 不同產氣量下管柱的橫向變形圖
因此,當產氣量增加時,會增大完井管柱的橫向變形,加劇了管柱與套管之間碰撞和摩擦,嚴重時會使完井管柱破壞。所以在滿足生產需求的情況下,應適當地降低產氣量,這有利于減小管柱的橫向變形,減輕管柱與套管碰撞,降低管柱與套管之間碰撞摩擦產生的損傷。
2.3 井口壓力對完井管柱振動特性的影響
圖6為不同井口壓力p1下管柱在5、10、15和20 s時的橫向變形圖。
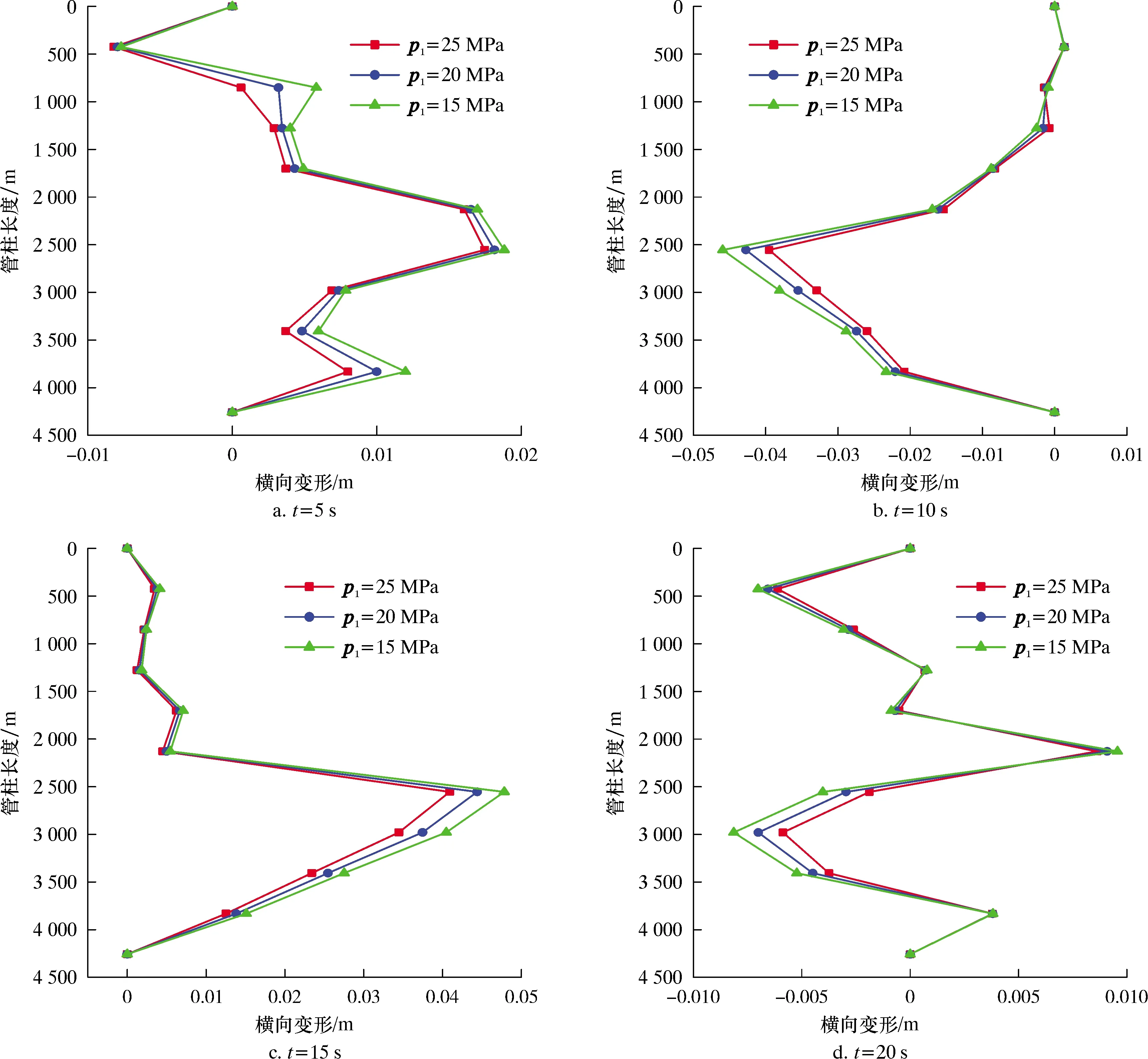
圖6 不同井口壓力下管柱的橫向變形圖
從圖6可以看出,管柱的橫向變形隨著井口壓力的減小而增大。這是因為井口壓力降低時,井筒上下的壓差增大,從而使管柱內的氣體產出壓差增大,氣體的鼓脹效應增強,氣體對管柱的作用力增大,管柱的變形增大[14-15]。適當增加井口壓力,可以減小完井管柱的橫向變形,減少管柱與套管的碰撞,從而降低管柱碰撞造成的損傷。
2.4 氣體密度對完井管柱振動特性的影響
圖7為不同氣體密度下管柱在5、10、15和20 s處的橫向變形圖。從圖7可以看出,管柱的橫向變形隨著氣體密度的增加而增大。這是因為氣體密度增加時,氣體和完井管柱之間的摩擦耦合效應增加,氣體的壓能更多地轉化成管壁的振動能量,所以管柱振動產生的變形增大[16]。
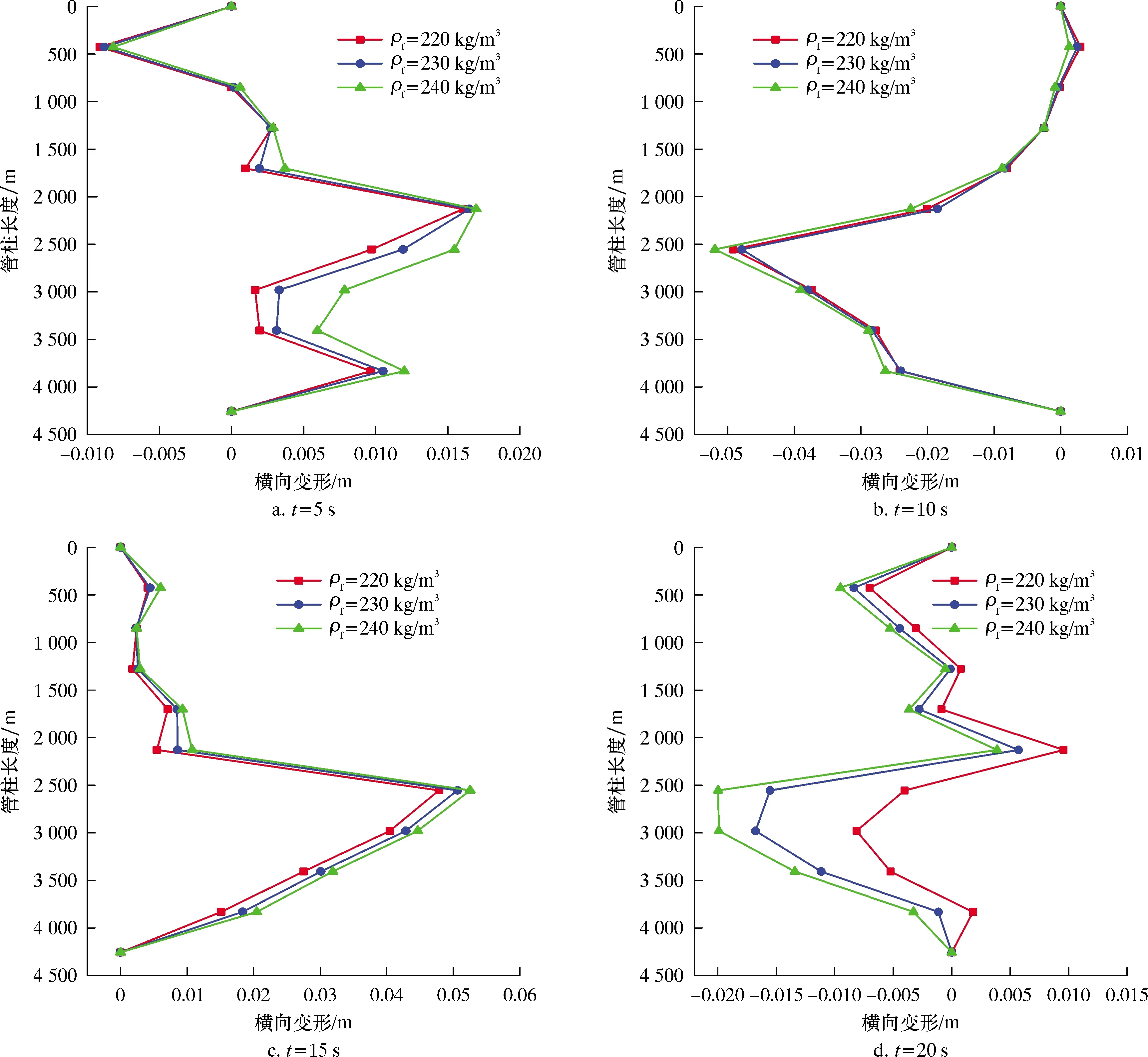
圖7 不同氣體密度下管柱的橫向變形圖
3 結論及認識
(1)針對完井管柱考慮了管柱橫向和縱向耦合振動,建立了氣井完井管柱流固耦合模型。
(2)在閥門開啟瞬間,高壓氣體通過完井管柱,管柱發生劇烈的振動,而后管柱的振動呈現衰減趨勢。在管柱振動衰減的過程中,管柱的最大橫向變形出現在管柱的中下段,管柱與套管易發生碰撞而產生安全問題。
(3)增加產氣量或降低井口壓力,管柱內的氣體對管柱的作用力都增大,使得管柱的橫向變形都將增大。氣體密度增大時,氣體與完井管柱之間的摩擦耦合作用加劇,管柱振動增強。
(4)在實際生產過程中,可以通過調節井口裝置降低產氣量或提高井口壓力,以此減輕管柱的振動,從而減少管柱與套管碰撞造成的損傷。

