軟懸掛撤離工況深水隔水管動力學特性分析*

柳 軍 王普檉 郭曉強

(西南石油大學機電工程學院)

0 引 言

隔水管系統是海洋平臺進行海底油氣開采與輸送中必不可少的關鍵設備。由于海洋環境的復雜性和多樣性，隔水管的安全性和穩定性遭到了挑戰，如深水鉆井平臺作業過程中遭遇強臺風時，為避免裝備發生破壞，保障作業安全，需要平臺懸掛隔水管撤離避開臺風。在平臺撤離時，隔水管受到劇烈的風、浪、流聯合作用，相比正常鉆井作業，懸掛撤離隔水管系統的外部更加惡劣，大大加劇了隔水管系統損壞的風險。

深水鉆井隔水管懸掛撤離方式有硬懸掛和軟懸掛兩種(硬懸掛方式：隔水管頂部與平臺進行剛性連接，平臺運動直接傳遞到隔水管頂部；軟懸掛方式：隔水管通過張緊器與平臺進行連接，伸縮節被鎖死，隔水管的重力由張緊器和大鉤承擔)。為了確保懸掛撤離隔水管系統的可操作性，國內外學者針對硬懸掛撤離做了一系列研究，建立了硬懸掛撤離工況下隔水管一維振動模型[1-5]和縱橫耦合二維振動模型[6]。部分學者[7-9]在軟懸掛與硬懸掛對比研究中發現，硬懸掛的隔水管系統比軟懸掛的隔水管系統對海況和干濕重力比更敏感，且相比硬懸掛，軟懸掛不易導致隔水管出現動態壓縮或頂部極端張力，同時上部撓性接頭可以避免隔水管出現較大的橫向集中載荷。孫友義等[10-11]研究了硬、軟懸掛結構下超深水立管的軸向動態特性，并討論了立管的防臺風管理策略。隨著數值技術的不斷發展，大長徑比結構的縱橫向耦合效應[12-15]和大變形[16-18]越來越被學者重視，為此，一些學者用CFD仿真法和半經驗法對海洋立管渦激振動展開研究[19-23]。以上研究闡述了軟懸掛的可行性和優勢，但現有研究主要集中于軟懸掛隔水管的縱向振動或者橫向振動，對軟懸掛隔水管的三維振動研究不足，而且未考慮大變形和流固耦合等非線性因素的影響。

基于此，本文考慮了縱向、橫流向和順流向三向耦合，以及渦激振動和大變形等非線性因素，建立了軟懸掛隔水管三維非線性振動模型，采用Newmark-β法和4階Runge-Kutta法實現了非線性振動模型的數值求解，借助文獻試驗參數及數據驗證了模型的正確性，探究了浮力塊布置和臺風重現期對軟懸掛撤離鉆井隔水管動態特性的影響規律，揭示了撤離工況下軟懸掛隔水管振動響應特性。

1 隔水管三維非線性振動模型

1.1 模型建立

1.1.1 隔水管振動控制方程

以隔水管未發生變形時垂直軸為z軸，向下為正，取隔水管上部為坐標原點，以水流平行方向為x軸，垂直于水流方向為y軸，建立坐標系，如圖1所示。υx、υy、u分別表示隔水管上任意一點在x、y、z方向上的位移。

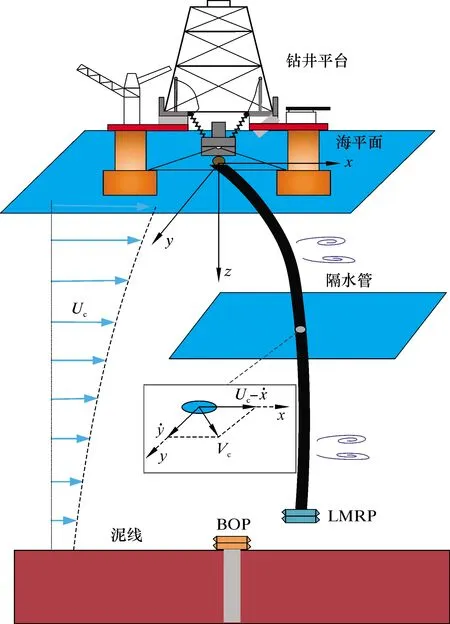
圖1 隔水管坐標系及其示意圖

假設隔水管為小變形，根據基爾霍夫假設：

(1)

式中：u1、u2、u3為與坐標系x、y、z對應的位移場函數。

基于給出的假設，則格林應變為：

(2)

將式(1)代入式(2)可得：

(3)

根據應變能的定義，隔水管應變能表示如下：

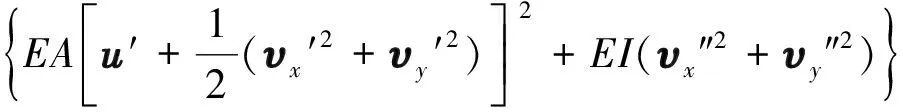
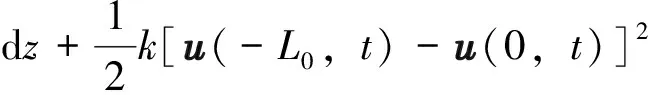
(4)

式中：E為彈性模量，Pa；I為慣性矩，m4；A為隔水管截面面積，m2。

在海洋鉆井和生產過程中，隔水管與半潛船或者鉆井船之間通過張緊器進行連接。張緊器等效彈簧剛度為[24]：

k=Wa/ac

(5)

式中：Wa為隔水管水下重力，N；ac為與隔水管張緊系統效率有關的常數[24]，本文取ac=10 m。

隔水管的動能可表示為：

(6)

式中：mυ為單位長度隔水管質量，kg；ρυ為隔水管密度，kg/m3；MTR為張緊環質量，kg；MLMRP為隔水管底部總成質量，kg。

結構阻尼、所受外部水動力及其阻尼所做功為：

(7)

式中：Fcx、Fcy、Fcz為結構阻尼力，N；FD、FL分別為外部流體順流方向的拖曳力與橫向方向的升力，N；wg為隔水管縱向力，N。

(8)

式中：ζ為結構阻尼比；ma為單位隔水管附加流體質量，kg；ωs為簡支隔水管固有角頻率；Do為隔水管外徑，m；ρw為海水密度，kg/m3。

根據哈密頓(Hamilton)原理和變分原理，聯立式(7)和式(8)可得隔水管3個方向振動方程：

(9)

1.1.2 海洋流體力

設流體與隔水管之間的相對速度為vr，隔水管外流速度為uc。基于定常流動，作用在管子上的穩態拖曳力和升力如圖2所示。

圖2 作用在隔水管上的外部流體力示意圖

根據Morison方程，則作用在隔水管上穩態拖曳力及升力為：

(10)

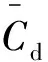
由圖2可知：

(11)

作用在隔水管x方向和y方向上的穩態流體力分量為：

(12)

作用在隔水管上除了穩態的流體分量外，還包括諧和形式的脈動拖曳力和脈動升力。

(13)

式中：FD′、CD、FL′、CL分別為脈動拖曳力、脈動拖曳力系數、脈動升力及脈動升力系數。

聯立式(11)～式(14)可得到作用在隔水管上的外部流體力：

(14)

采用Van der Pol非線性振動方程描述流體漩渦的脫落特性[25]，其尾流振子控制方程為：

(16)

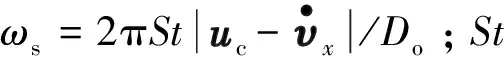
脈動拖曳力系數CD和脈動升力系數CL分別通過順流向和橫流向無量綱尾流振子變量qx和qy表示，即：

(17)

將公式(17)代入公式(15)，可得作用在隔水管上的外部流體力最終形式：

(18)

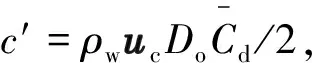
(19)

根據實際的軟懸掛撤離工況，隔水管上端與張緊器連接，下端自由，模型的邊界條件可以寫成：

(20)

式中：uboat(t)為平臺升沉運動的函數,m/s；Ku為上部撓性接頭的旋轉剛度，N·m/(°)。

1.2 模型求解

(21)

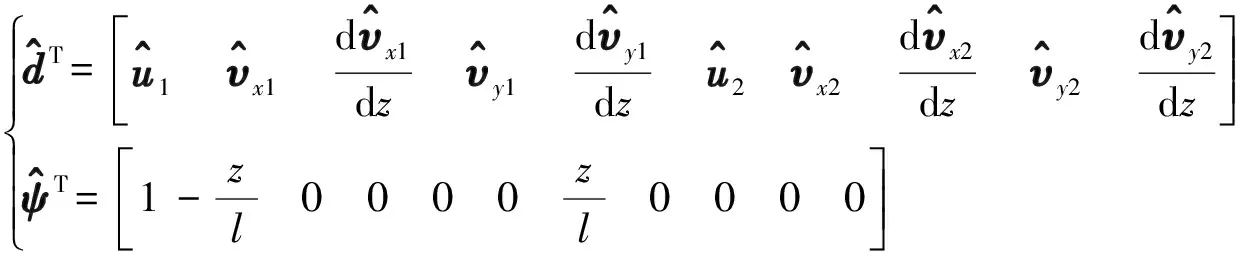
(22)

(23)

將單元隔水管控制方程進行矩陣組裝，可得隔水管振動控制矩陣方程為：

(24)

式中：M為系統的質量矩陣，C為系統的阻尼矩陣，K為系統的剛度矩陣，D為系統的位移，F為系統的外力矩陣。

由于隔水管考慮了縱橫向耦合因素，且隔水管模型的剛度矩陣會隨著位移實時發生非線性變化，為了更好地適應隔水管非線性的影響，采用Newmark-β法[6]積分實現隔水管振動模型的數值求解，尾流振子模型采用4階龍格庫塔進行求解，求解流程圖如圖3所示。

圖3 鉆井隔水管非線性動力學模型的求解流程

采用Fortran語言編寫了隔水管非線性振動響應計算代碼。

1.3 模型的驗證

此案例采用SONG L.J.等[27]的試驗數據進行驗證，其物理試驗在上海船舶運輸科學研究所拖曳水池中進行，試驗中上、下兩端鉸接。算例參數如下：隔水管長度7.9 m，水深7.9 m，外徑0.030 m，內徑0.027 m，頂張力2.943 kN，彈性模量108 GPa，海水密度1 000 kg/m3，單位長度隔水管質量1.768 kg/m，外流速度0.4和2.8 m/s，結構阻尼系數0.003。

邊界條件使用公式(25)。

(25)

圖4和圖5為不同均勻外流流速下，隔水管位移均方根分布驗證圖。由圖4和圖5可知，隔水管各振動模態都與試驗結果非常接近，表明本文所建模型有效。

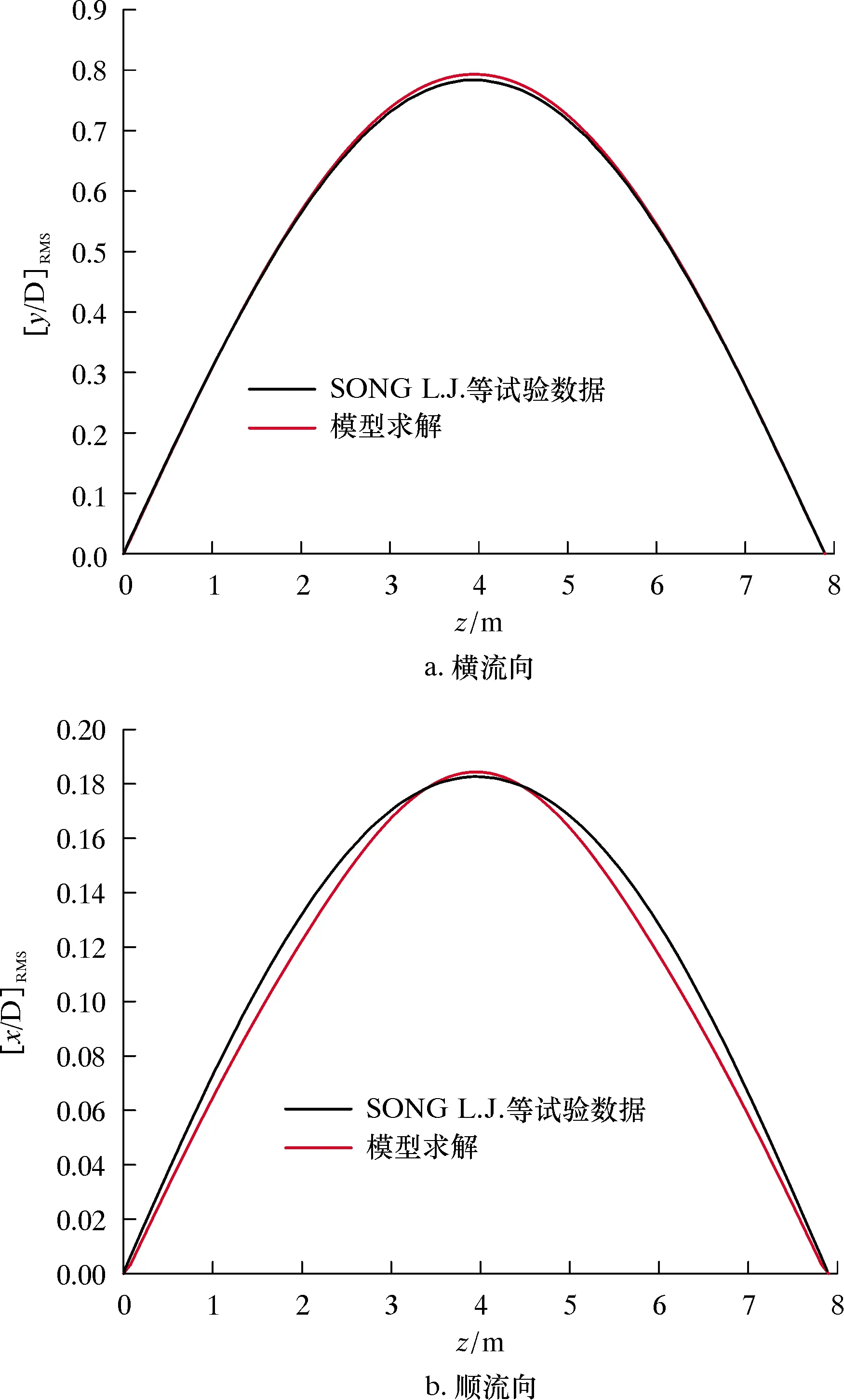
圖4 外流速度U=0.4 m/s下隔水管位移均方根分布驗證圖

由圖4還可以看出，隔水管在外流速度為0.4 m/s時，本文模型數值結果與試驗在隔水管橫流向與順流向均表現為1階振動模態，本模型所得的隔水管位移均方根數值結果與試驗所得位移均方根數值結果在隔水管橫流方向與順流方向均非常接近。

由圖5可知：隔水管外流速度為2.8 m/s時，隔水管在橫流方向，本模型數值結果與試驗所得的振動模態均表現為5階；在順流方向，本模型與試驗所得的振動模態均表現為7階。同時在隔水管位移均方根幅值方面，由圖5a可知，隔水管橫流方向上本文模型數值結果與試驗結果在隔水管兩端處有一定差別，但越靠近中間，兩者越接近。由圖5b可知，隔水管順流方向兩者結果越靠近中部越接近。這可以證明本文所采用的隔水管非線性振動控制模型及尾流振子模型對于隔水管非線性振動的模擬有效。

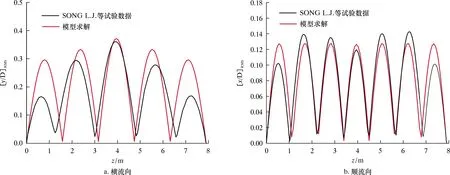
圖5 外流速度U=2.8 m/s下隔水管位移均方根分布驗證圖

2 隔水管振動響應特性分析

基于非線性動力學模型研究軟懸掛撤離中隔水管的動態行為[28-29]。計算模型的基本參數如表1所示，南海海流和海浪環境參數如表2所示。

2.1 不同浮力塊布置

本節研究了不同浮力塊覆蓋率fp(0%、25%、50%、75%和100%)下軟懸掛隔水管動力學響應，結果如圖6～圖8所示。相關計算參數見表1。

表1 計算模型

由圖6可以看出：順流向位移隨浮力塊覆蓋率的增加而增加，主要是因為浮力塊增加了隔水管的外徑以及順流方向上的阻力；底部處于低流速區，同時受隔水管底部總成質量的影響，中部順流向位移時程響應的振動幅值高于底部的振動幅值。過大的順流向位移會增加隔水管上端與月池的碰撞風險，因此，浮力塊的配置比例應控制在一定范圍內，不宜過大。

圖6 順流向的位移響應

由圖7a和圖7b可以看出：浮力塊覆蓋對隔水管橫向位移均方根和應力的影響較大；隔水管最大均方根位移對應的浮力塊覆蓋率為75%，最大應力均方根對應的浮力塊覆蓋率為75%，這一結果同齊娟娟等[3]的研究結果趨勢相近。值得注意的是，在覆蓋率為25%的情況下，隔水管會產生較低階的振動，同時均方根應力也較小，而在100%的覆蓋率下，隔水管會產生相對高階的振動，同時均方根應力也較大。由圖7c和圖7d可以看出：在50%和75%的覆蓋率下橫流向振動幅度更大，而且頻帶分布更廣；在0%的覆蓋率下橫流向振動幅值較小，頻率更高。

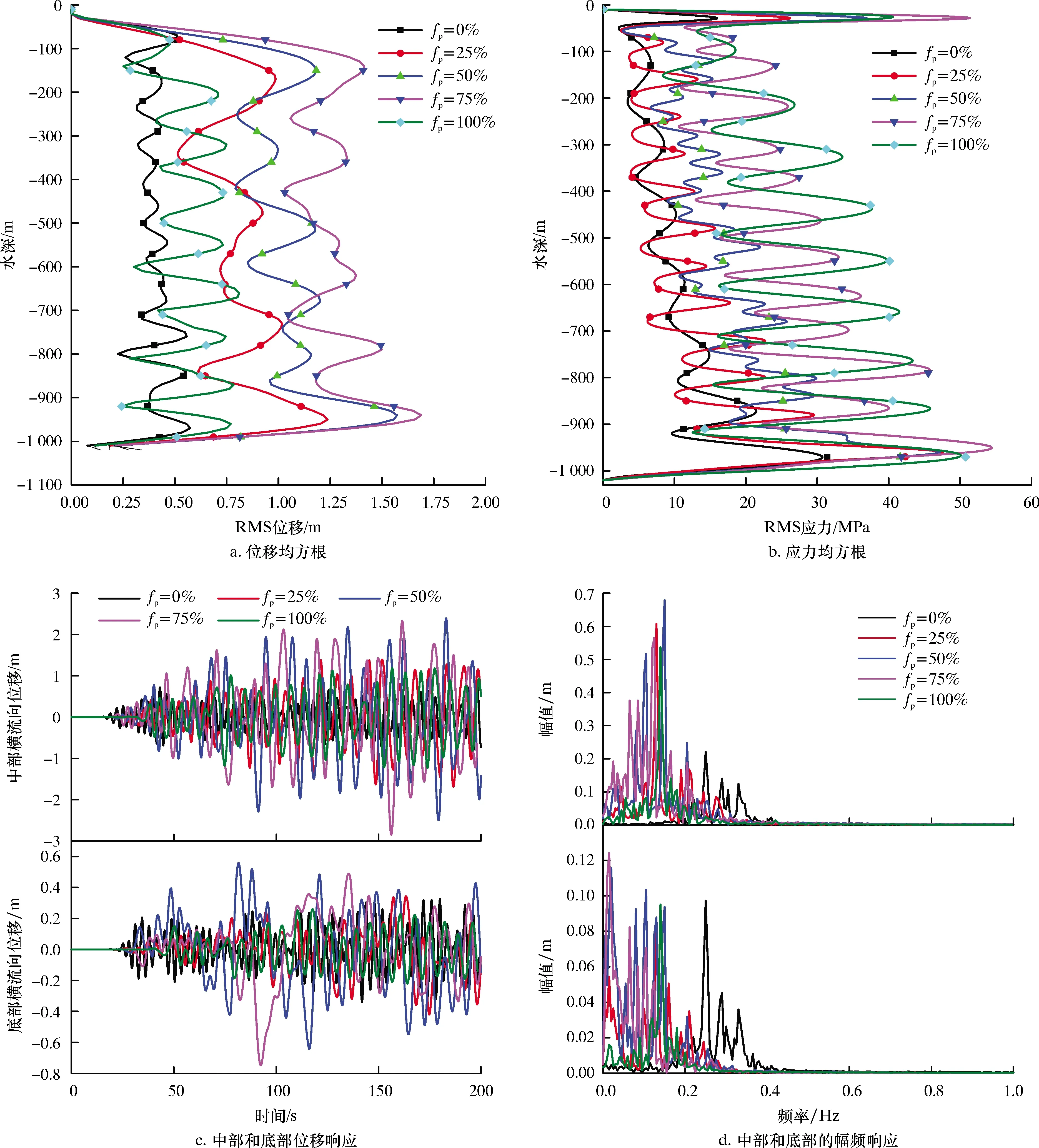
圖7 橫流向的位移響應

由圖8a可知，浮力塊覆蓋度的變化對縱向振動的頻率沒有顯著影響，但對振動的振幅有影響。由圖8b可知，浮力塊能有效地減小隔水管的濕重，覆蓋率越高，縱向振動的位移幅值和最大動態軸力越小。

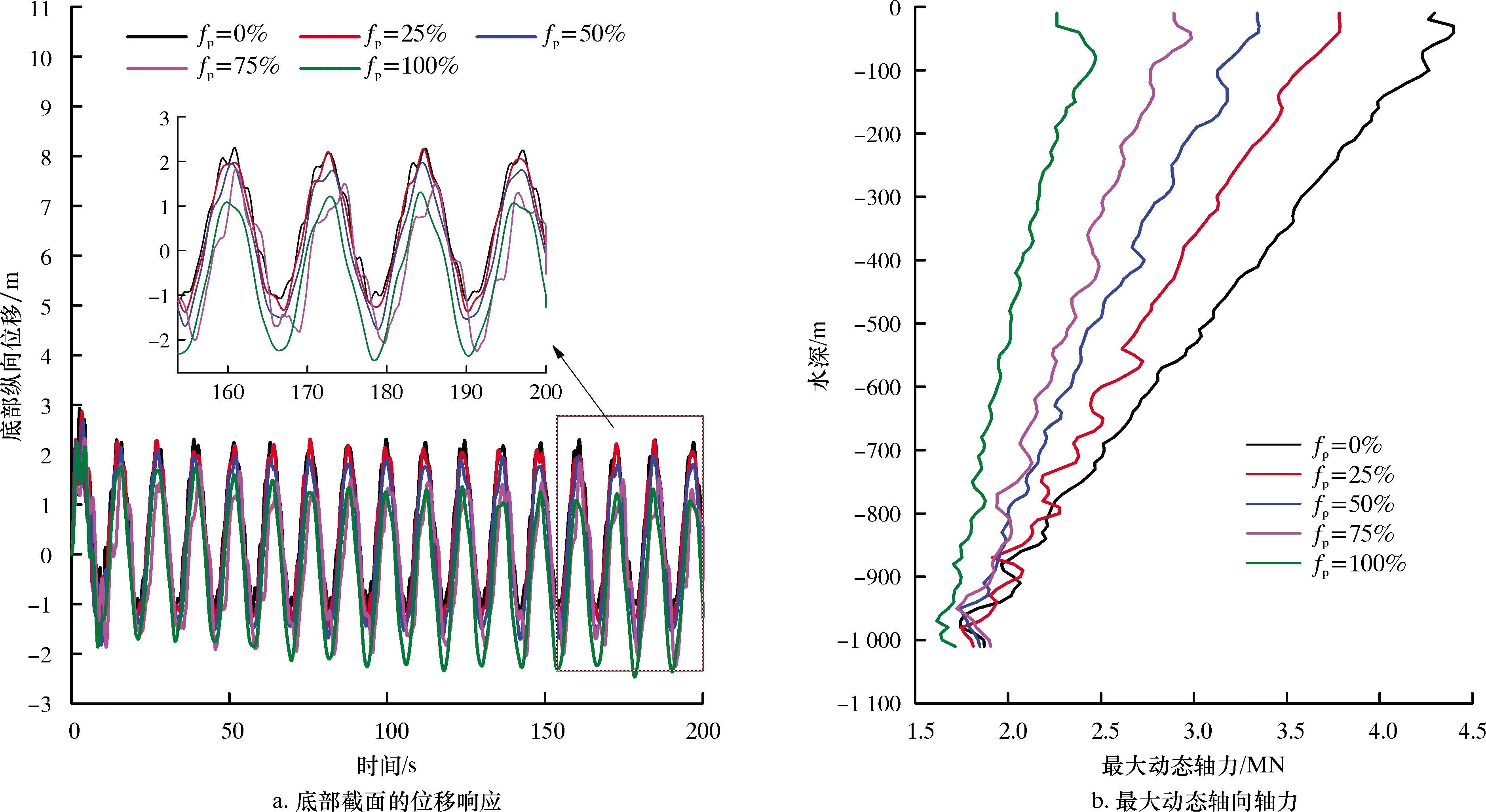
圖8 縱向動力學響應

2.2 臺風重現期T的影響

以 HYSY981 鉆井平臺在1 005 m水深下的實際隔水管系統配置為例：額定深度1 524 m的隔水管16根，額定深度為2 286 m的隔水管2根，額定深度為3 048 m的隔水管27根，壁厚25.4 mm的裸管8根(自上而下排列)。分析不同臺風重現期下隔水管系統避臺風撤離動力學特性響應。相關參數選取如表2和表3所示。

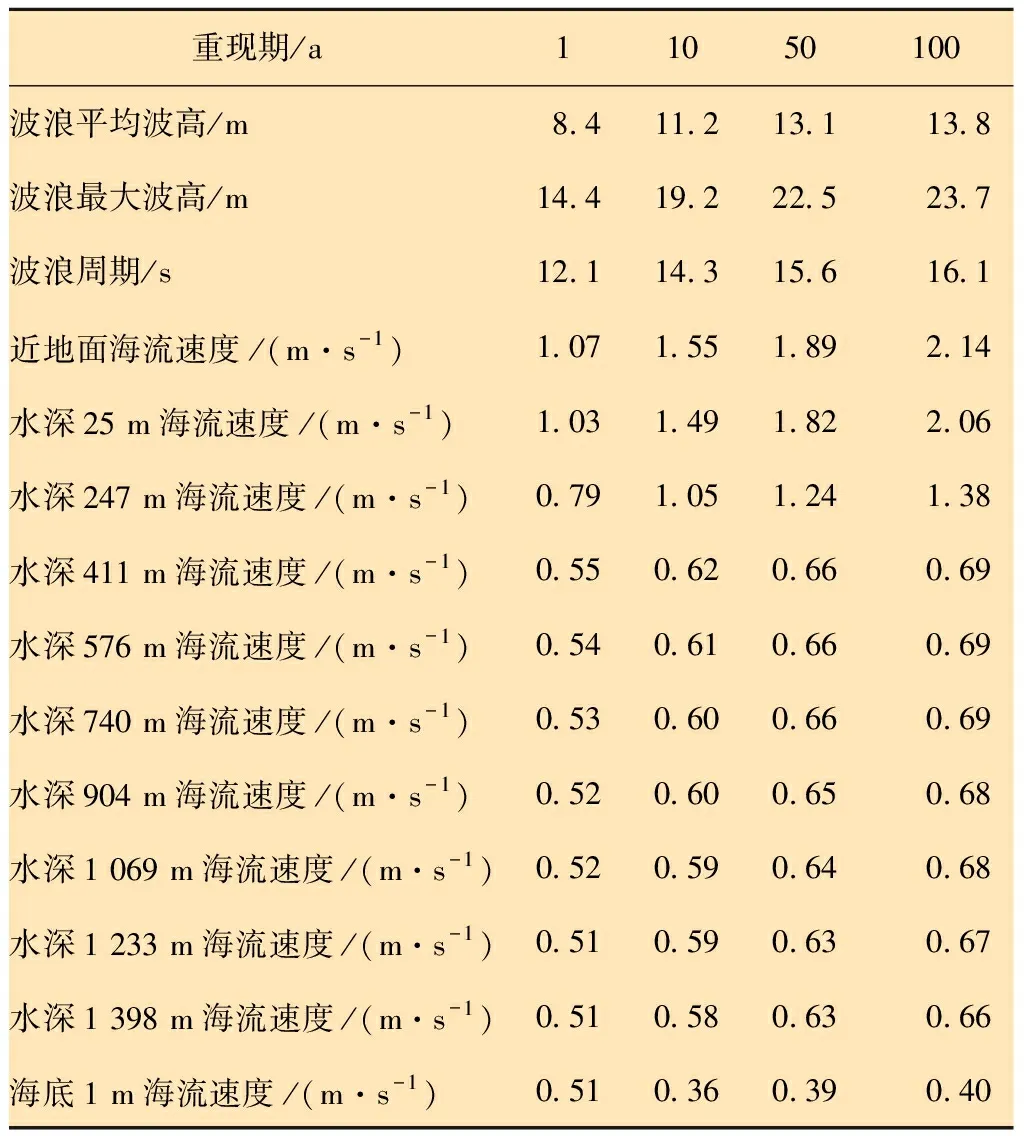
表2 南海海流和海浪環境參數[3]

表3 HYSY981鉆井平臺隔水管系統基本參數[3]

分析不同臺風重現期下，海流速度和平臺深沉周期的變化會對軟懸掛撤離隔水管動力學響應產生的影響，結果如圖9所示。由圖9可知，臺風重現期越長，波浪和海流越大，50和100 a一遇的臺風重現期下，隔水管的橫流向RMS位移、橫流向RMS應力和縱向位移最大，順流向RMS位移隨重現期的延長而依次增大。

由圖9a和圖9b可知：不同臺風重現期在0～411 m水深間都處于高流速區，在靠近低端區域，4種重現期工況下的RMS位移和振動模態階數相差不明顯，而在高流速區的橫流向RMS位移和振動模態階數隨著流速的增加而增加，同時變得更復雜，橫流向RMS應力也隨之增大；在水深800 m以下，RMS應力出現減小的趨勢，這是因為在這個區域中隔水管無浮力塊的影響。由圖9c可知：隔水管靠近上部的彎曲程度較大，這是高流速區和浮力塊導致的結果；由于高年限臺風重現期的波浪幅值更大，導致縱向振動幅值更大。

圖9 隔水管動力響應

3 結 論

(1)針對緊急撤離工況下深水隔水管振動失效問題，采用有限元法并結合哈密頓變分和虛功原理，建立了軟懸掛鉆井隔水管三維非線性動力學模型，考慮了縱橫向耦合效應、海洋渦激效應以及隔水管的大變形等非線性因素。采用Newmark-β法和4階Runge-Kutta法實現了非線性振動模型的數值求解，借助文獻試驗參數和測試數據驗證了理論模型的正確性，為揭示撤離工況下軟懸掛隔水管響應特性奠定了模型基礎。

(2)采用所建立的軟懸掛隔水管非線性振動模型和南海現場參數，探究了浮力塊布置模式對軟懸掛隔水管振動響應的影響規律。研究結果表明，合理布置浮力塊可以減小振動位移、應力和動態軸力，當浮力塊覆蓋率為25%的情況下，隔水管產生低階的振動模態，同時均方根應力也較小，能夠有效提高隔水管的安全性。

(3)探究了不同臺風重現期工況下軟懸掛隔水管的振動響應。研究結果表明，懸掛撤離工程中，流速和浮力塊對隔水管的影響不可忽略，在高流速區中，隔水管的浮力塊布置應該減少，在靠近頂部或者底部區域會出現應力和位移的最大值，現場需重點關注此位置處隔水管的安全性。