溫差作用下回接套管柱井口抬升影響分析*

于 浩 趙朝陽 練章華 曹金超 陳宇杭 李 帥

(西南石油大學油氣藏地質及開發工程國家重點實驗室)

0 引 言

在稠油油藏注蒸汽或高產氣井的開采過程中，由于井底高溫氣體作用，套管、水泥環及地層全部被加熱，使得套管及地層溫度升高而發生熱膨脹，進而產生熱應力。套管屬于熱理性金屬材料，會在溫差作用下產生膨脹，當套管端部受井口約束或受水泥石膠結作用而不能自由伸長時，套管上的應力會重新分布，產生軸向作用力。當溫差足夠大，產生的軸向作用力大于套管重力、水泥石膠合作用力和井口重力等外載荷時，套管將舉升井口，出現井口抬升現象。井口抬升會導致油氣井井筒完整性破壞，影響油井的后續生產安全，嚴重時可直接導致油井報廢。

關于井口抬升，國內外許多學者進行了大量研究。1996年，李子豐[1]通過結合固井和熱采過程，推導出注蒸汽過程中套管和注蒸汽管柱內各種應力的計算公式。1997年，J.C.R.PLACIDO等[2]發現，在同一熱循環載荷下殘余應力隨套管鋼級增加而增大。2004年，余中紅等[3]發現，當套管周圍掏空時其熱應變達到了2.0%，遠超過材料彈性極限應變(0.3%)。2012年，LING Q.J.[4]認為，當油壓和套壓都為0時，管柱內的熱應力總和就是作用在導管上的應力總和，且套管上熱應力和井口抬升量是未膠結段套管長度和溫度的函數。錢大偉等[5]為減小熱采井井口抬升對套管損壞的影響，設計了套管熱應力補償器。王建軍[6]通過建立套管-水泥環-地層的全井筒有限元模型，發現稠油熱采井在長期高溫注蒸汽作業中預拉力會因管體應力松弛現象而失效。王宴濱等[7]通過建立井口力學模型，發現井口總熱膨脹力及井口抬升量隨著各層套管溫度的升高呈線性增大。林元華等[8]通過建立多管柱井口抬升模型并結合多目標優化算法，形成了預測井口抬升量(高度)的新方法。張智等[9]提出自由套管段的溫度變化和各層套管水泥返深是影響井口熱應力及套管抬升的主要因素。2018年，徐剛等[10]發現，井口抬升是高溫產生熱載荷破壞固井界面膠結使自由套管產生上頂力而導致的。2019年，石小磊等[11]在溫度效應和鼓脹效應的基礎上，提出了螺旋屈曲效應，建立了精確的井口抬升高度預測模型。謝仁軍等[12]通過試驗研究了溫度及環空條件對井口抬升量的影響，并制定了井口抬升控制措施。2020年，謝仁軍等[13]又通過建立不同溫升條件下單層自由套管及多層套管耦合井口抬升量預測模型，得到溫室效應、環空上端部約束狀態和環空壓力等因素對井口抬升量的影響。余意等[14]分析了產量、生產時間、各環空壓力及固井情況等因素對井口抬升量的影響，得出了主要影響因素的強弱順序。

雖然以上學者對管柱熱應力、井口抬升機理以及預測等方面開展了大量研究，但關于回接套管柱在固井-生產作業過程中井口應力分布及抬升現象的研究卻少之又少。為進一步驗證井口應力及抬升高度預測模型在回接套管固井生產工況下的正確性，本文采用有限元法，根據順北區塊某井現場工況，利用ABAQUS軟件建立了不同工況下多層套管-水泥環-地層多體系統熱-固耦合分析模型，分析了回接套管從固井階段開始到生產時的應力和位移變化，得到井口應力及抬升高度變化過程及其相關參數的影響規律。所得結果可為現場回接套管柱井口抬升現象分析提供一定的參考。

1 井筒傳熱理論及井口抬升機理

1.1 多級井筒傳熱

實際井筒中存在多級套管，進而通過井口連接形成多級管柱系統。多層圓筒穩態導熱示意圖如圖1所示。

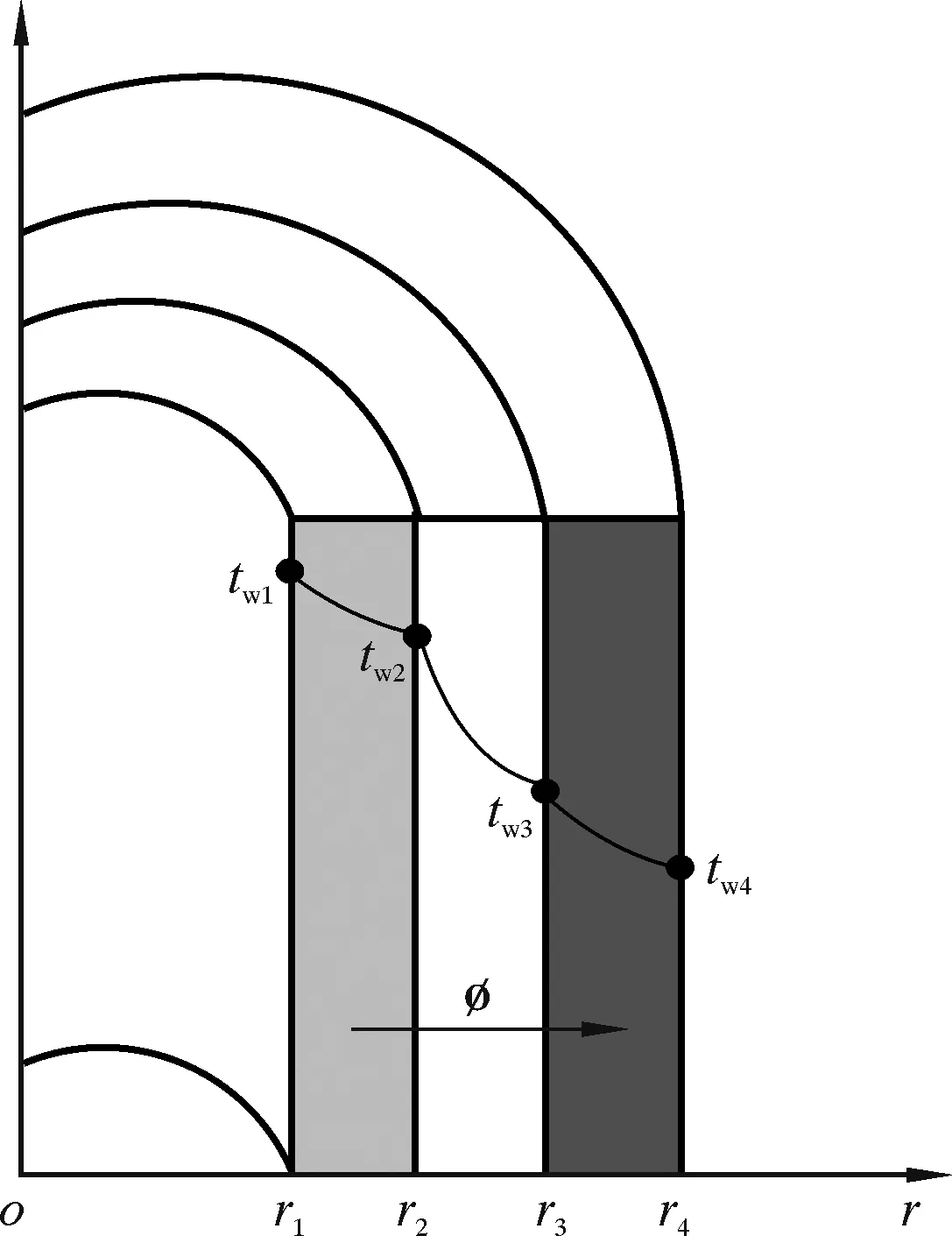
圖1 多層圓筒穩態導熱示意圖

將多層圓筒壁視為無內熱源，各層的導熱率為常數，內、外壁面維持均勻恒定的溫度tw1、tw2、tw3及tw4。由于通過各層圓筒壁的熱流量相等，且總導熱熱阻等于各層導熱熱阻之和，所以單位長度圓筒的導熱流量計算式為：

(1)

式中：λ1～λ4分別為各層圓筒的導熱率，d1～d4分別為各層圓筒的直徑。

以此類推，對于n層不同材料組成的多層圓筒壁的穩態導熱，單位長度的熱流量為：

(2)

1.2 井筒抬升量計算模型

實際生產中，井筒管柱的材料性能會隨著溫度的變化而變化，當溫度較低時，材料的熱膨脹系數較小，當溫度超過100 ℃以后，材料熱膨脹系數明顯大于常規值，說明高溫下材料的熱膨脹效應更加強烈。在溫度一定時，套管的熱膨脹系數為定值，于是套管線膨脹量計算公式為：

ΔL=εL=αΔTL

(3)

式中：ΔL為套管軸向線膨脹量，m；ε為溫度應變；L為管柱長度，m；α為套管熱膨脹系數，℃-1；ΔT為溫度變化量，℃。

井口套管熱膨脹效應對井口產生的作用力計算式為：

(4)

將式(3)代入式(4)，得：

Fti=αiΔTiEiAi

(5)

式中：Fti為第i層套管熱膨脹對井口產生的作用力，N；σi為第i層套管井口熱膨脹應力，Pa；ΔLi為第i層套管產生的線膨脹量，m；Li為第i層套管長度，m；Ei為第i層套管材料的彈性模量，Pa；Ai為第i層套管材料井口的橫截面積，m2。

2 自由拉伸及固井工況下數值模擬

2.1 有限元模型建立

順北地區的高溫氣井之所以會出現井口抬升或井口應力集中現象，可以從溫度和壓力兩個因素來分析。首先這些油氣井套管升溫較大，使油套管出現井口未固井或固井質量差、井段套管軸向伸長；其次，由于油套管壓力大，使其發生鼓脹或反鼓脹效應，在溫度和壓力的綜合作用下導致井口出現抬升現象筆者根據現場數據建立了多層套管-水泥環-地層多體系統熱-固耦合分析有限元模型，如圖2所示。該模型是耦合熱-固軸對稱模型，模型軸向長為1 000 m，橫向只有10 m。為了顯示更為清楚，將其橫向放大1 000倍。

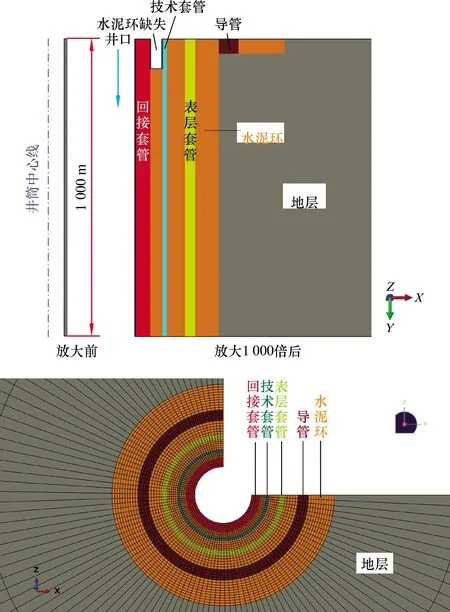
圖2 多層套管-水泥環-地層多體系統熱-固耦合分析有限元模型

為準確反映在井筒溫度場作用下實際回接套管的受力及變形情況，本文從套管下放到井筒中底部自由伸長狀態開始模擬計算，并利用單元生死技術對伸長后的套管進行約束以模擬固井作用；然后模擬井底流體在流向井口過程中的熱傳遞和溫度場分布，以及不同套管和水泥環地層的應力變化；最后釋放井口以獲取井口抬升高度，分析步驟如圖3所示。

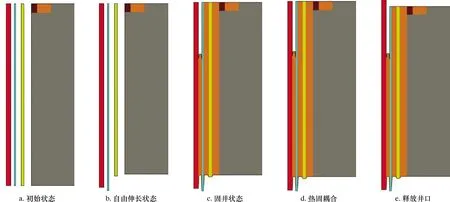
圖3 有限元分析步驟示意圖

2.2 套管下放自由拉伸狀況

在井口固定的情況下，套管柱受到自身浮重及下部管柱拉伸作用會向下自由伸長，并產生一定的拉伸應力。圖4反映了套管在浮重及下部管柱拉伸作用下的應力及位移分布情況。由圖4可以看出：套管的最大Mises應力出現在井口位置，值為306.3 MPa，最大位移出現在技術套管1 000 m處，值為1.207 m，井口位置的拉伸位移為0；對于回接套管而言，最大Mises應力同樣出現在井口位置，值為231.0 MPa，最大拉伸位移出現在回接套管底部，值為0.953 m。由此可知，地層中所有套管上的應力都遠小于其材料的屈服強度，表明此時地層中的套管處于安全的受力范圍。

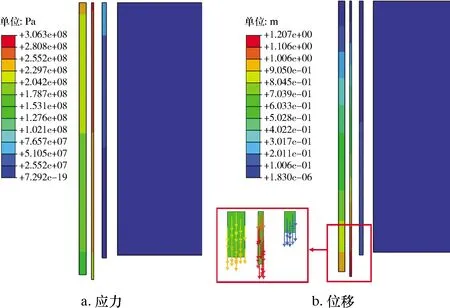
圖4 套管在浮重及下部管柱拉伸作用下的應力及位移分布云圖

2.3 固井作業工況

固井作業過程中由于水泥漿的凝固膠結作用，使不同套管及地層形成一個新的整體，套管上由于浮重及下部套管拉伸作用所產生的位移和變形被封固在地層中，進而形成一個新的系統。根據現場工況，研究井筒中套管柱在不同溫差及水泥漿返高情況下的溫度場、應力場及位移分布情況。圖5為固井作業后套管的應力及位移分布云圖。由圖5可知，套管的應力和位移與自由拉伸狀況時很相近，變化不大。

圖5 固井作業后套管應力及位移分布云圖

3 井筒套管井口應力及抬升分析

在一定溫差下，不同材料都會產生膨脹趨勢，在井筒中由于不同材料間熱膨脹系數的差異以及井口上的固定約束，使不同材料的應力相對于固井后的應力會產生一定變化。圖6反映了井筒溫差為150 ℃下水泥漿分別返高至地面、100 m、200 m及300 m時地層溫度場分布情況。由圖6可知：最高溫度都出現在回接套管下部，最高溫度為155 ℃，回接套管在井口處的溫度為142 ℃，證明井底流體在向井口流動的過程中存在一定能量損失；在徑向上，溫度從回接套管內壁上的最高溫度逐漸降低至原場地層溫度，衰減模式與套管水泥環和地層的熱力學參數相關。

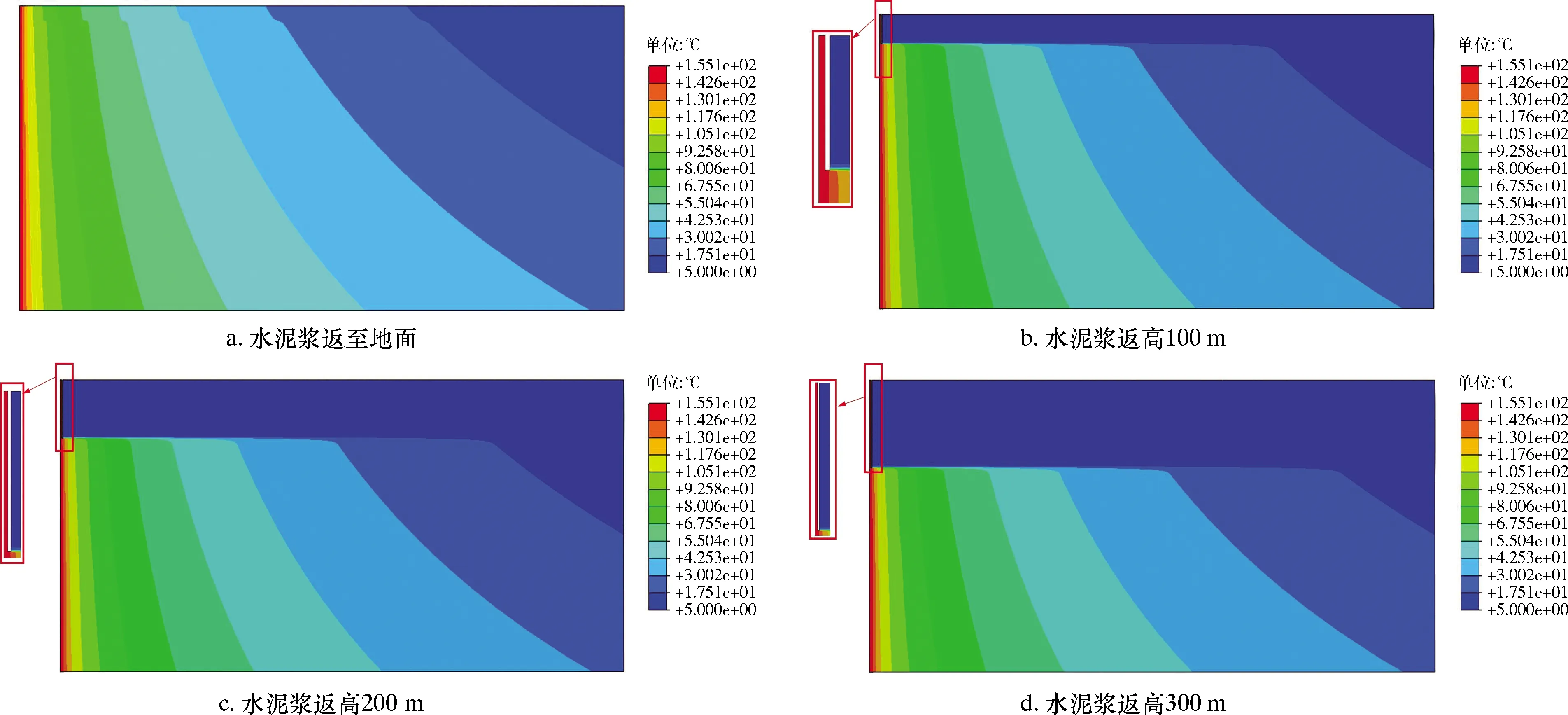
圖6 井筒溫差為150 ℃時，不同水泥漿返高下井筒溫度場分布云圖

經過150 ℃的溫差作用，使不同材料都發生了一定的膨脹。但是由于不同材料間熱膨脹系數的差異以及井口的固定約束，會使不同材料的應力相對于固井后的應力出現一定變化。圖7反映了在井筒溫差為150 ℃，當水泥漿返高分別至地面、100 m、200 m及300 m地層時回接套管應力分布情況。由圖7可知：當水泥漿返高至地面時，回接套管井口處應力僅為38.3 MPa，相對于固井后的231.0 MPa減小了192.7 MPa，這是因為水泥環良好的膠結和封固作用，有力地限制了回接套管的熱膨脹，套管的熱膨脹作用不僅沒有使回接套管應力增大，反而抵消了一部分浮重作用下的自由伸長，緩解了回接套管井口處的應力；當水泥漿分別返高至100、200及300 m時，回接套管柱最大應力分別為278、286和274 MPa，相對于固井后的231 MPa分別增大了47、55及43 MPa。這表明水泥環的缺失使相應缺失段的套管在溫差作用下產生了較大的熱應力。

圖7 井筒溫差為150 ℃時，不同水泥漿返高下井筒Mises應力分布云圖

圖8反映了在井筒溫差為150 ℃，當水泥漿返高分別至地面、100 m、200 m及300 m地層時，井口約束釋放后的套管應力場、位移場及拉升量變化情況。

圖8 不同水泥漿返高下井口約束釋放后的套管應力場、位移場及井口抬升量云圖

由圖8可知：在卸載掉井口位置的約束后，水泥漿返高至地面時，回接套管頂部Mises應力減小到37 MPa，與卸載約束前的應力值相比并未發生太大變化，與此同時，回接套管也并未出現任何抬升，證明水泥環的封固作用可以有效約束套管的熱膨脹；但是當水泥漿返高至100、200及300 m時，回接套管頂部Mises應力都下降至0，相比于卸載約束前應力發生了明顯變化；卸去井口約束后，回接套管都出現了一定的抬升現象，井口抬升位移分別為0.171、0.356及0.499 m。

圖9為井筒溫差為150 ℃時，水泥漿返高對回接套管應力及抬升量的影響曲線。由圖9可以看出：最大Mises應力出現在水泥漿返高120 m時，最大應力值為317.3 MPa；隨著水泥漿返高的增加，井口抬升高度單調增加。這表明隨著水泥環缺失的嚴重性增加，套管自由段數越長，在溫差作用下可伸長抬升的高度也就越大。隨著水泥漿返高的增加，井口固定時的回接套管的Mises應力先增加、后降低(見圖7)，并不呈現單調遞增或遞減的趨勢。這表明雖然回接套管伸長總量隨水泥漿返高的增加而增加，但是單位長度的熱膨脹伸長量也會受到固井前套管浮重及下部管柱拉伸作用下的反向伸長影響，使得單位長度回接套管的伸長量隨水泥漿返高的增加而不再呈現單調變化趨勢。

圖9 不同水泥漿返高時井口約束釋放后井口抬升量及回接套管井口處Mises應力曲線

4 結 論

(1)通過有限元軟件建立了多層套管-水泥環-地層多體系統熱-固耦合分析模型，分析了回接套管從下入井筒時的拉伸狀態到固井后套管上的熱應力分布狀態。

(2)隨著水泥漿返高的增加，井口抬升高度單調增加，這表明隨著水泥環缺失的嚴重性增加，套管自由段數越長，在溫差作用下可伸長抬升的高度也就越大。

(3)隨著水泥漿返高的增加，井口固定時回接套管的Mises應力先增大、后減小，并不呈現單調遞增或遞減趨勢。這表明雖然回接套管伸長總量隨水泥漿返高的增加而增加，但是單位長度的熱膨脹伸長量也會受到固井前套管浮重及下部管柱拉伸作用下的反向伸長影響，使得單位長度回接套管的伸長量隨水泥漿返高的增加而不再呈現單調變化趨勢。