基于脈沖式力源的發動機試車臺矢量推力校準裝置設計及仿真

黃相華 楊海生 江 峰 楊水旺 宋志強

(1.北京振興計量測試研究所，北京 100074；2.火箭軍裝備部駐北京地區第六軍事代表室，北京 100070)

1 引 言

在發動機研制生產環節中，推力測試是評估發動機性能極為重要的參數之一。矢量推力測量數據的準確性直接關系到矢量發動機的性能，從而很大程度上影響著后續矢量發動機的研制、驗證試驗、飛行試驗等[1]。

隨著發動機矢量推力測量日益受到重視，發動機矢量推力校準也逐漸成為困擾發動機設計部門與試驗部門的一個難題。目前，已經建設完成的試車臺，推力校準基本還是采用實驗室送檢的方式進行。即把發動機試車臺上的力傳感器拆下后，送到有資質的實驗室進行校準，再裝回到發動機試車臺上進行試驗測試。

傳統推力校準方法存在以下幾個問題。

1)測力傳感器的校準是在理想靜態環境下進行的，得到靈敏度系數，但是在實際測試環境中測量的是動態力值信號，測量數據誤差較大；

2)矢量推力測量系統的各個測量儀器只能單獨進行校準，不能做到系統校準，對于整個測量系統的測量不確定度無法有效評估；

3)目前在用的發動機試車臺，僅局限于對推力進行單分量校準，通過計算公式將各個方向的推力合成，得到矢量推力的校準結果，與發動機實際工作狀況存在較大差異。

通過分析可知，傳統的校準方式已經不適應飛速發展的矢量推力試驗技術[2-7]。本文提出一種基于脈沖式力源的發動機試車臺校準裝置，對試車臺進行矢量推力校準。設計完成后對校準方案進行了動力學建模及仿真，對測量結果進行了測量不確定度評估。

2 矢量推力現場動態校準方案

2.1 矢量推力校準技術方案的確定

發動機試車臺上矢量推力測量系統在試驗時，可以分別測得主推力Fx和側向力Fy，Fz，矢量推力的幅值大小即可由空間正交力的形式表示。當矢量推力測量系統測得空間正交力Fx，Fy，Fz的幅值大小后，可通過式(1)計算，從而得到矢量推力F為

(1)

而發動機試車臺矢量推力的另外一個參數，偏斜角α可以通過式(2)計算得出

(2)

由此可以看出，把主推力和側向力各個方向的傳感器都進行動態校準后，就可保證通過公式計算矢量推力大小和偏斜角大小的準確度。本項目的研究重點是動態校準裝置設計，設計原理總體框圖如圖1所示，并通過數采系統分別得到矢量推力校準裝置和試車臺矢量力測量系統的力值曲線，通過比較法實現力傳感器動態校準，進而保證矢量推力測量系統測量結果的準確性。

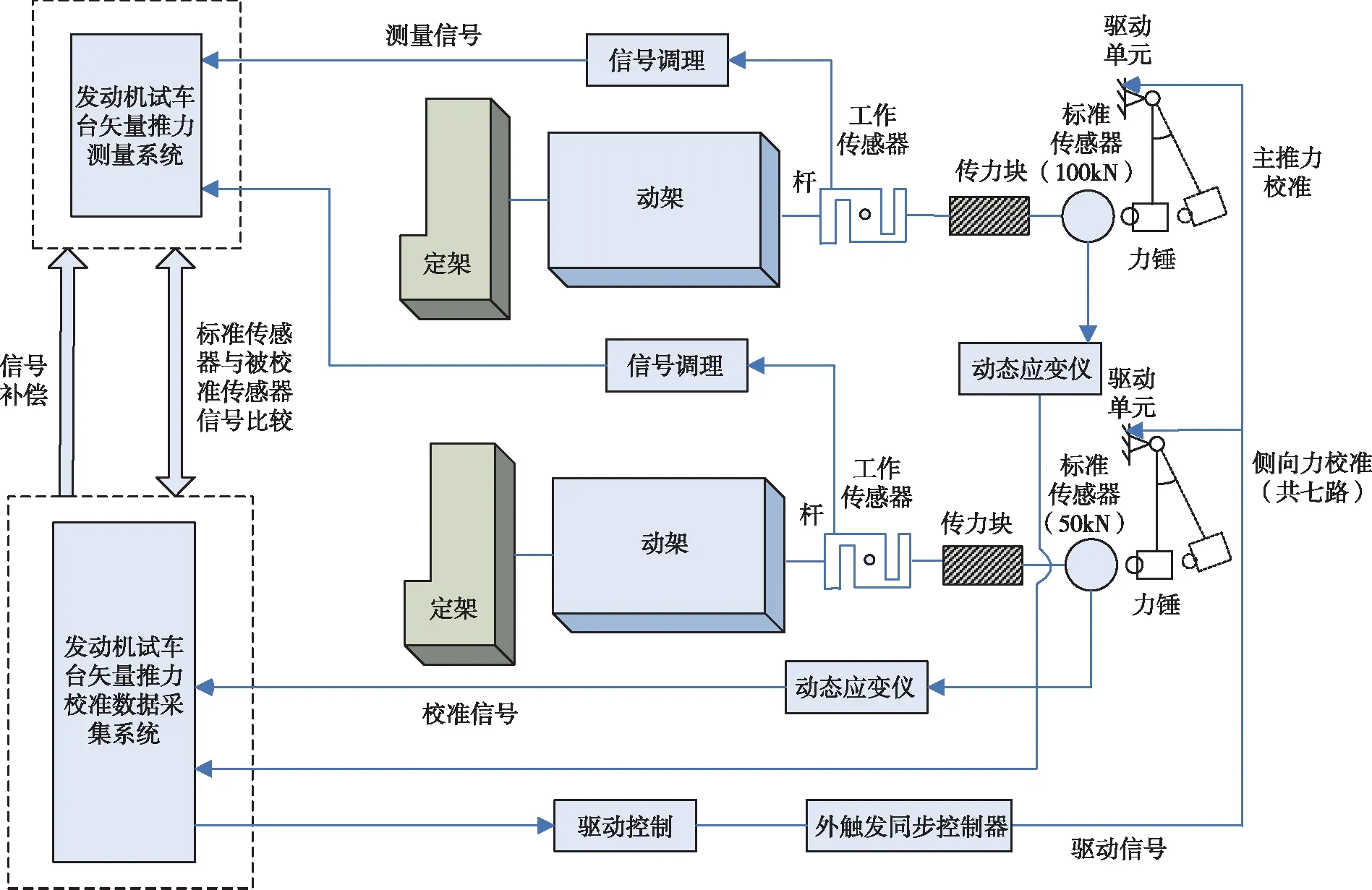
圖1 發動機試車臺矢量推力校準總體框圖

通過調研，對現階段已經得到應用的矢量力發生裝置的優點及缺點進行比較[8-12]，確定了采用擺錘式動態力發生裝置作為現場矢量推力校準的動態激勵源，以完成發動機試車臺矢量推力的校準工作。

整套校準裝置根據施加作用力的方向與力值的大小，可以分為主推力校準模塊與側向力校準模塊。在進行校準時，根據需要提供的激勵波形，調整校準擺錘激勵系統的工作參數，如擺錘的提升高度、擺動角度、擺錘的錘頭質量等，可以獲得不同幅值與脈寬組合的半正弦沖擊力信號。

隨后將校準裝置所采集到的標準動態力信號，與矢量推力測量系統采集到的測試數據進行比較。通過數據融合、矢量推力動態特性的獲取、測量系統幅頻相頻特性的補償等數據處理方法，實現發動機試車臺矢量推力的現場校準。

2.2 擺錘式脈沖激勵裝置的設計

發動機試車臺矢量推力現場動態校準是通過矢量推力校準裝置和試車臺矢量力測量系統之間比對來實現，而擺錘式動態力發生裝置用于提供一個便于測量和分析的半正弦力值信號。擺錘式的矢量推力激勵裝置機械結構如圖2所示。

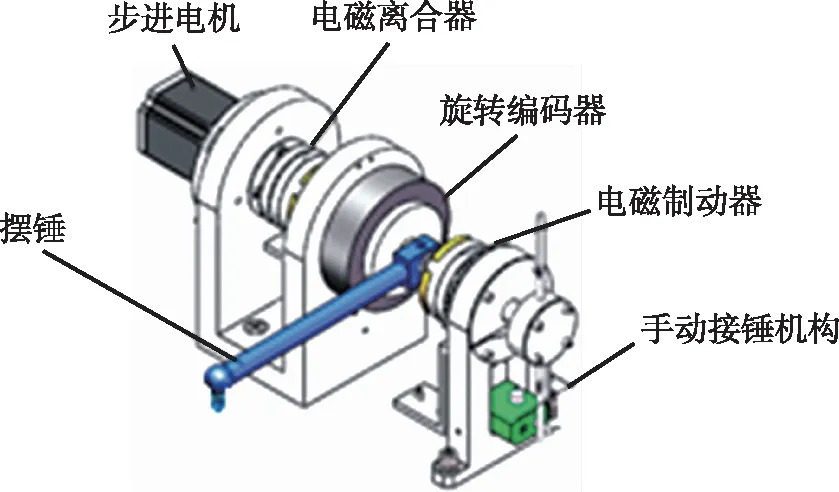
圖2 激勵裝置機械結構圖

為了能夠快速便捷產生一定幅值和脈寬半正弦力值信號，需要對擺錘工作狀態參數(錘頭質量、擺臂長度、擺動角度、材料剛度等)與其所產生動態力之間數學關系進行進一步理論分析和仿真研究。為確保擺錘動態力幅值準確度和穩定度，需對擺錘擺動角度精確定位。通過相應機電元件測出擺錘擺動角度，并反饋至控制單元，通過驅動電機精確控制擺錘擺動高度。

2.3 傳力塊的設計

為產生便于分析與測量的半正弦激勵信號，擺錘式矢量力發生裝置通過撞擊傳力塊，得到不同脈寬、不同幅值的沖擊力值信號。

傳力塊與擺錘錘頭以及工作級傳感器連接方式如圖3所示，圖中傳力塊采用40Cr或炮鋼材料，其上放置可換材料，產生校準所需脈寬。

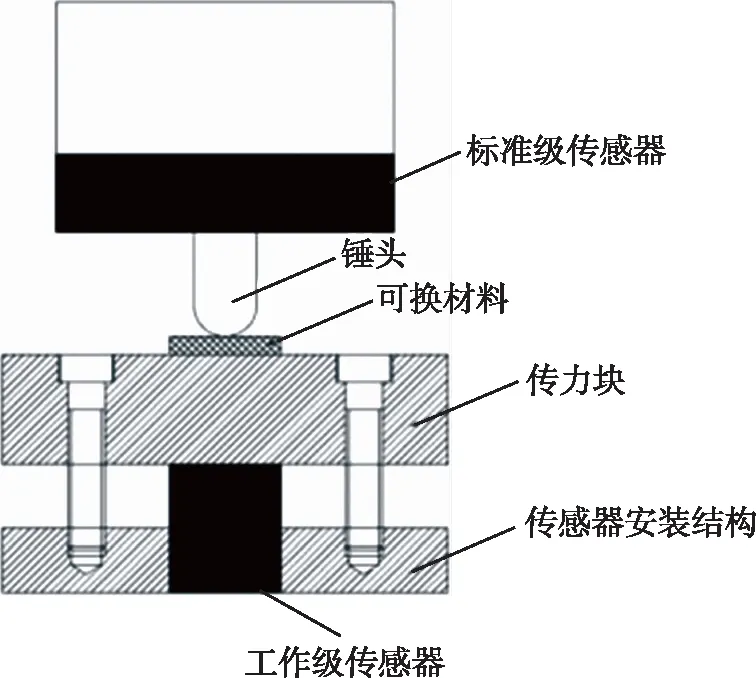
圖3 傳力塊結構圖

假定可換材料為規則形狀，受力面積為A，厚度為T的條件下，線性恢復力系數k有關系式為

(3)

式中：E0——可換材料的初始彈性模量。

根據式(10)，可換材料可設計成圓柱體或長方體型等規則形狀，若保證可換材料受力面積和厚度之比A/T為0.1，則系數k近似等于E0/10，根據仿真結果，可換材料初始彈性模量E0應控制在(0.5～10)GPa范圍內，因此可選擇聚乙烯(0.49～2.50)GPa、尼龍(1.07～2.83)GPa、酚醛塑料(3.92～8.83)GPa和鉛17GPa等不同初始彈性模量材料作為可換材料使用。

為了使得撞擊力能夠盡可能沿著垂直于工作級傳感器敏感面方向進行傳遞，當擺錘式動態力發生裝置錘頭與可換材料接觸時，錘頭與傳感器敏感面近似保持垂直狀態。此外還需調節好擺錘錘頭與傳力塊對中精度，從而進一步保證傳力方向與工作級傳感器垂直度在誤差允許范圍之內。

3 脈沖式力源的力學仿真分析

3.1 模型的建立

根據前文的分析可知，通過合理調整系統參數，如擺錘質量、提升角度、可換材料等即可獲得不同脈寬及幅值力值信號[13]。擺錘式動態力發生裝置的力學模型如圖4所示。

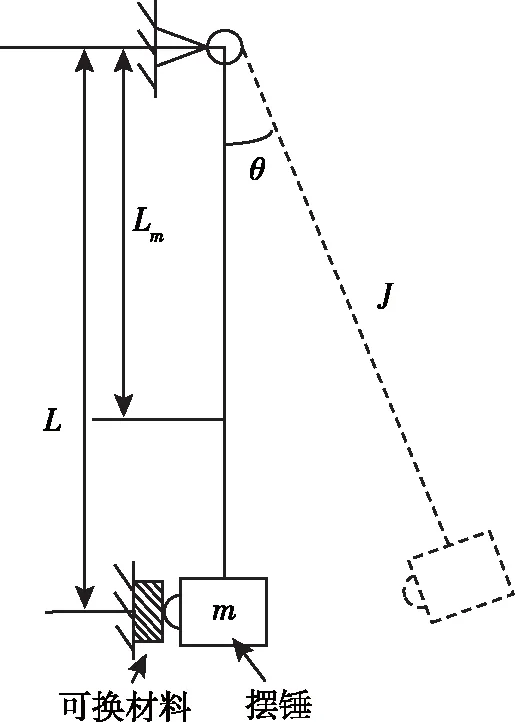
圖4 擺錘式激勵裝置力學模型圖

將擺錘激勵系統進行簡化，擺錘視為理想剛體，其幾何尺寸不隨沖擊力值的變化而變化。取擺錘為研究對象，擺錘撞擊可換材料的初始角速度ω由擺錘的提升角度θ來決定。

當擺錘激勵系統中的擺錘從初始位置到達擊打位置時，擺錘所能達到的勢能為

Ep=mgLm(1-cosθ)

(4)

式中：Lm——擺錘擺桿系統質心到轉動中心的長度；m——擺錘質量；θ——擺錘提升角度。

當擺錘激勵系統的擺錘到達擊打位置時，其動能可以用式(5)表示

(5)

式中：J——擺錘相對于轉動中心點的轉動慣量。

將擺錘系統視為理想狀態時，根據能量守恒定律，可以認為擺錘激勵系統Ep=Ek。

由此可以得到擺錘在撞擊傳力塊前的沖擊速度為

(6)

式中：L——轉動中心與擺錘擊打點之間的距離。

考慮到在設計時擺錘激勵裝置中擺錘質量遠大于擺桿，擺錘自身尺寸相對較小，和擺桿相比可忽略，因此擺錘質心到轉動中心距離Lm和轉動中心到擺錘沖擊點距離L近似相等，擺錘對擺動中心轉動慣量J≈mL2，則有

(7)

以擺錘旋轉至與可換材料碰撞瞬間為時間零點，可換材料與擺錘的接觸點為坐標原點，根據牛頓第一定律，可以得到擺錘激勵系統的力學方程為

(8)

一般在工程應用中，可更換材料一般可以分為雙曲正切型非線性材料、正切型非線性材料、三次型非線性材料等幾個種類。在本項目中，采用的是三次型非線性材料，故而，擺錘的彈性恢復力可以用式(9)表示

F(x)=kx+δx3

(9)

式中：k——線性恢復系數；δ——非線性恢復系數。

將式(9)代入式(8)，變換后，可以得到擺錘激勵系統的擺錘力學方程為

(10)

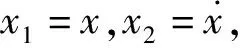
(11)

采用數值計算法，利用Matlab對上述二元一階常微分方程組進行求解，可以得到所需的計算結果。

為詳細分析擺錘沖擊過程中的變量對沖擊力幅值和沖擊力脈寬等數值的影響，在設計之初可以分別以可換材料的k，δ,θ，m,L等為變量，對設計方案進行仿真，并分析各種變量對最終產生的半正弦沖擊力所產生的影響。

3.2 沖擊過程的半正弦力值時域與頻域仿真

為了便于分析，設擺錘裝置打擊傳力塊產生的力脈沖信號為理想半正弦，則力脈沖信號可表示為

(12)

式中：Fm——脈沖力峰值；τ——脈沖力脈寬。

選取半正弦力脈沖信號幅度譜密度由1下降至0.1的頻率段作為信號的有效頻帶，分別對脈寬為0.1ms，0.5ms和1ms的歸一化理想半正弦力脈沖信號進行分析，得到的頻譜仿真圖如圖5和圖6所示。

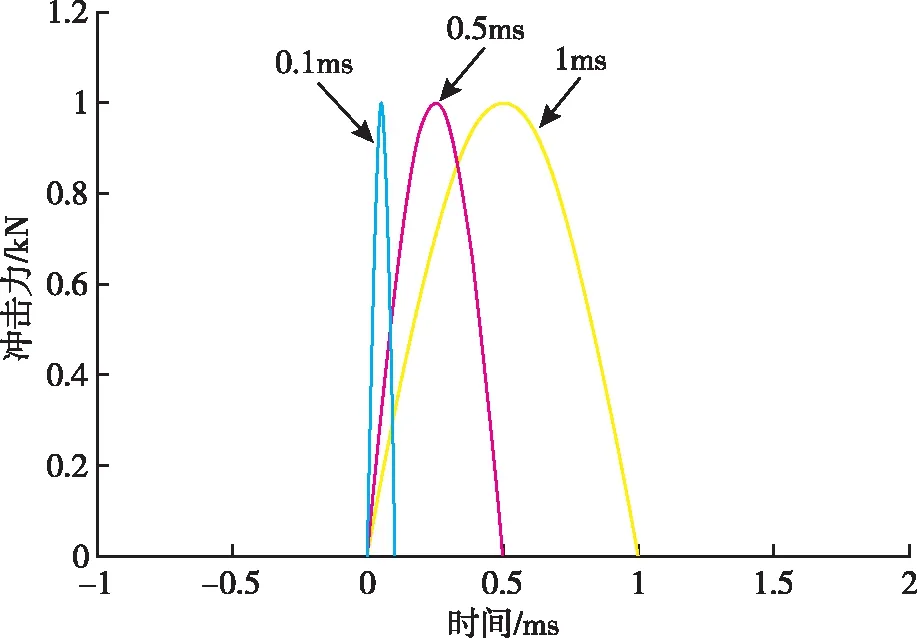
圖5 沖擊過程的半正弦力值時域仿真圖

從圖5和圖6可知，脈寬為0.1ms，0.5ms和1ms的歸一化理想半正弦力脈沖信號的有效頻帶范圍分別為13 120Hz，2 607Hz和1 303Hz，為了達到技術指標，力脈沖信號的脈寬應控制在1.3ms以內。

3.3 激勵系統的沖擊力仿真結果

下面針對各種參量作為設計變量，分別加以仿真，以驗證所設計擺錘激勵系統的結果[14]。

3.3.1不同k值條件下沖擊力仿真

根據設計輸入條件，確定初始條件：擺錘激勵系統的初始擺角θ=90°，材料的非線性恢復系數δ=1×1010，擺錘的質量m=5kg，轉動中心到擺錘沖擊點的距離L=1m，在線性恢復力系數k=[5×107，l×l08，2×108，5×108]的不同條件下，利用Matlab進行數值仿真，得到在不同k值下的擺錘激勵系統沖擊力值曲線，如圖7所示。

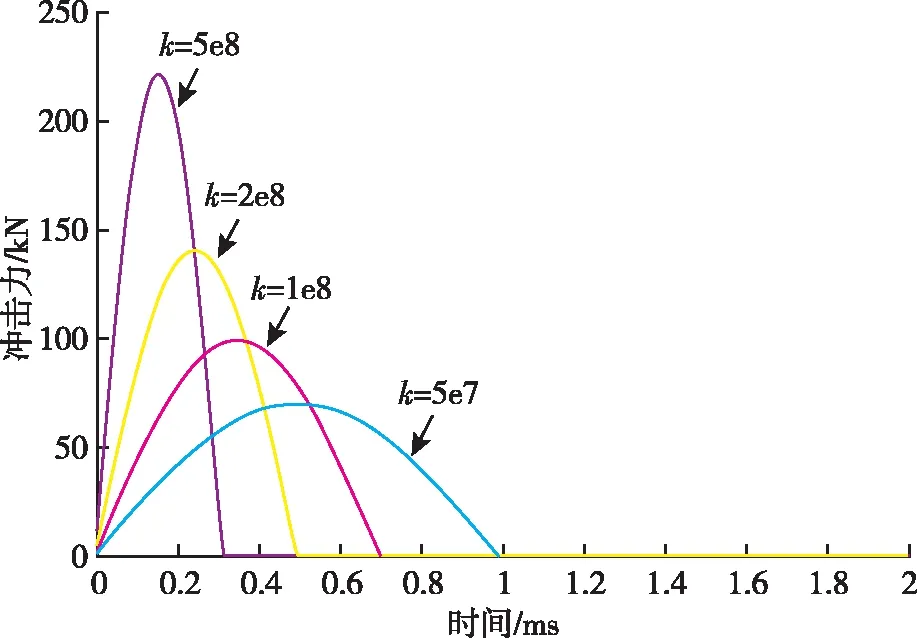
圖7 不同k值條件下沖擊力仿真圖

從圖7中的仿真結果可以看出，激勵源在沖擊過程中產生的為半正弦式脈沖力波形，其脈沖力幅值與可更換材料的k值大小成正比，而脈沖力的脈寬與可更換材料的k值大小成反比。材料的線性恢復力系數k對脈沖力的幅值和脈寬的影響均較大。

3.3.2不同δ值條件下沖擊力仿真

選取仿真初始條件：[k,θ,m,L]=[5×106，90°，10，1]，分別取δ=[0，l×1010，5×1010，1×1011]，仿真得到的不同δ值下的擺錘激勵系統沖擊力值曲線，如圖8所示。

圖8 當k=5×106時不同δ值下沖擊力仿真圖

選取仿真初始條件：[k,θ,m,L]=[1×107，90°，5，1]，分別取δ=[0，1×109，1×1010，1×1011]，仿真得到的不同δ值下的擺錘激勵系統沖擊力值曲線，如圖9所示。

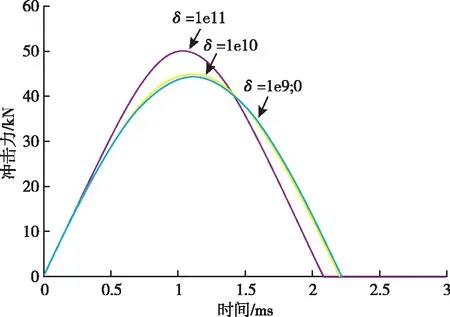
圖9 當k=1×107時不同δ值下沖擊力仿真圖

選取仿真初始條件：[k，θ，m，L]=[1×108，90°，5，1]，分別取δ=[0，1×109，1×1010，1×1011]，仿真得到的不同δ值下的擺錘激勵系統沖擊力值曲線，如圖10所示。

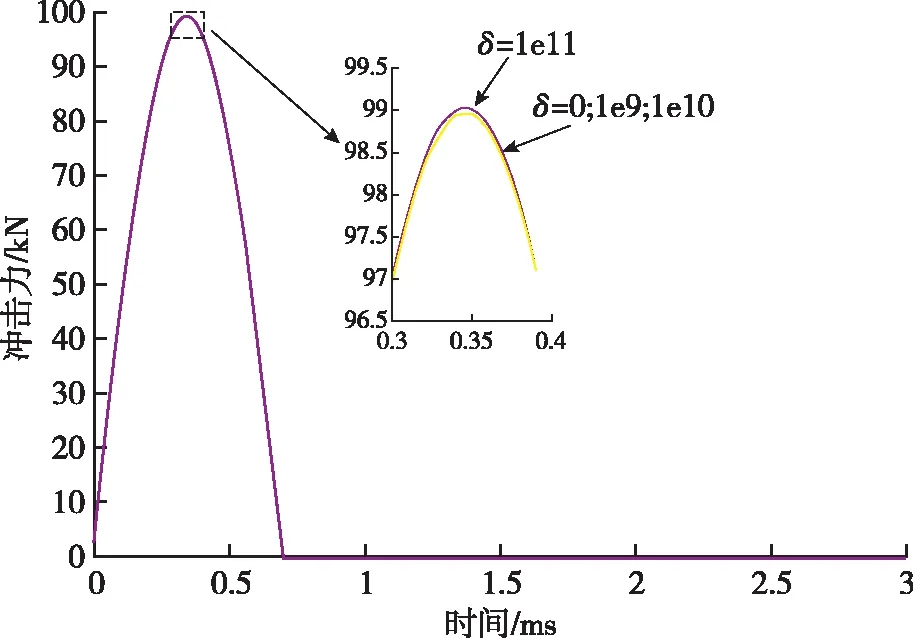
圖10 當k=1×108時不同δ值下沖擊力仿真圖

從仿真結果可以看出，擺錘沖擊過程中隨著δ的增加，沖擊力峰值增大，而脈寬則隨之減小。

這說明在設定了相同的試驗參數時，當可換材料的非線性恢復系數越大時，擺錘激勵系統所產生的動態力幅值就越大，沖擊力脈寬越窄；反之，當可換材料的非線性恢復系數越小時，擺錘激勵系統所產生的動態力幅值就越小，沖擊力脈寬也越寬。

3.3.3不同θ值條件下沖擊力仿真

選取仿真初始條件：[k，δ，m，L]=[1×108，1×1010，5，1]，分別取θ=[30°，60°，90°，120°]，得到在不同擺角條件下擺錘激勵系統沖擊力值曲線，如圖11所示。

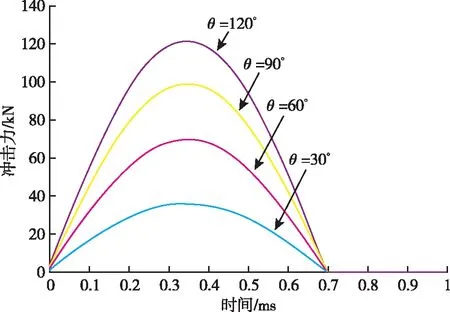
圖11 不同θ值條件下沖擊力仿真圖

從仿真得到的結果可以看到，激勵系統的θ值越大，脈沖力的幅值越大，而脈沖力的脈寬在改變θ值的過程中變化不大。

3.3.4不同m值條件下沖擊力仿真

選取仿真初始條件：[k,θ,δ,L]=[1×108，90°，1×1010，1]，分別取m=[1，5，10，15]，得到在擺錘質量不同的條件下擺錘激勵系統沖擊力值曲線，如圖12所示。

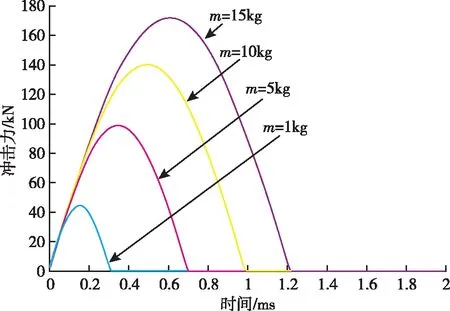
圖12 不同m值條件下沖擊力仿真圖

由圖中的仿真結果可以看到，隨著錘頭質量m的增大，激勵系統的脈沖力幅值與脈寬均會增大，且脈沖力幅值增大的幅度更明顯。

3.3.5不同L值條件下沖擊力仿真

選取仿真初始條件：[k,θ，δ，m]=[1×108，90°，1×1010，5]，分別取L=[0.5，1，1.5，2]，得到在L值不同的條件下擺錘激勵系統沖擊力值曲線，如圖13所示。

圖13 不同L值條件下沖擊力仿真圖

擺錘沖擊過程中的力峰值隨著L的增加而增大，而力脈寬則隨著L的增加而減小。轉動中心到擺錘沖擊點的距離L對力信號峰值影響較大，對脈寬影響較小。

從分析可知通過合理的調整系統參數即可獲得不同脈寬及幅值的力值信號。根據上文中的仿真結果，本項目主要通過改變擺錘質量m、擺桿長度L、擺動角度θ和可換材料線性恢復力系數k這四個參數來控制力脈沖信號的峰值和脈寬。其中，擺錘質量可通過設計多組不同質量(0.1kg，0.2kg，0.5kg，1kg，2kg和5kg)的組合式配重片來進行調節；擺桿長度可通過設計多組不同長度(0.1m，0.5m和1m)的擺動桿來進行調節；擺動角度在0°～120°范圍內可調。

4 試車臺矢量推力測量不確定度分析

依據現場的校準過程，提煉出發動機試車臺矢量推力測量不確定度分量，進行分析，并加以匯總，進行測量不確定度的合成[15]。測量不確定度分量評估表見表1。

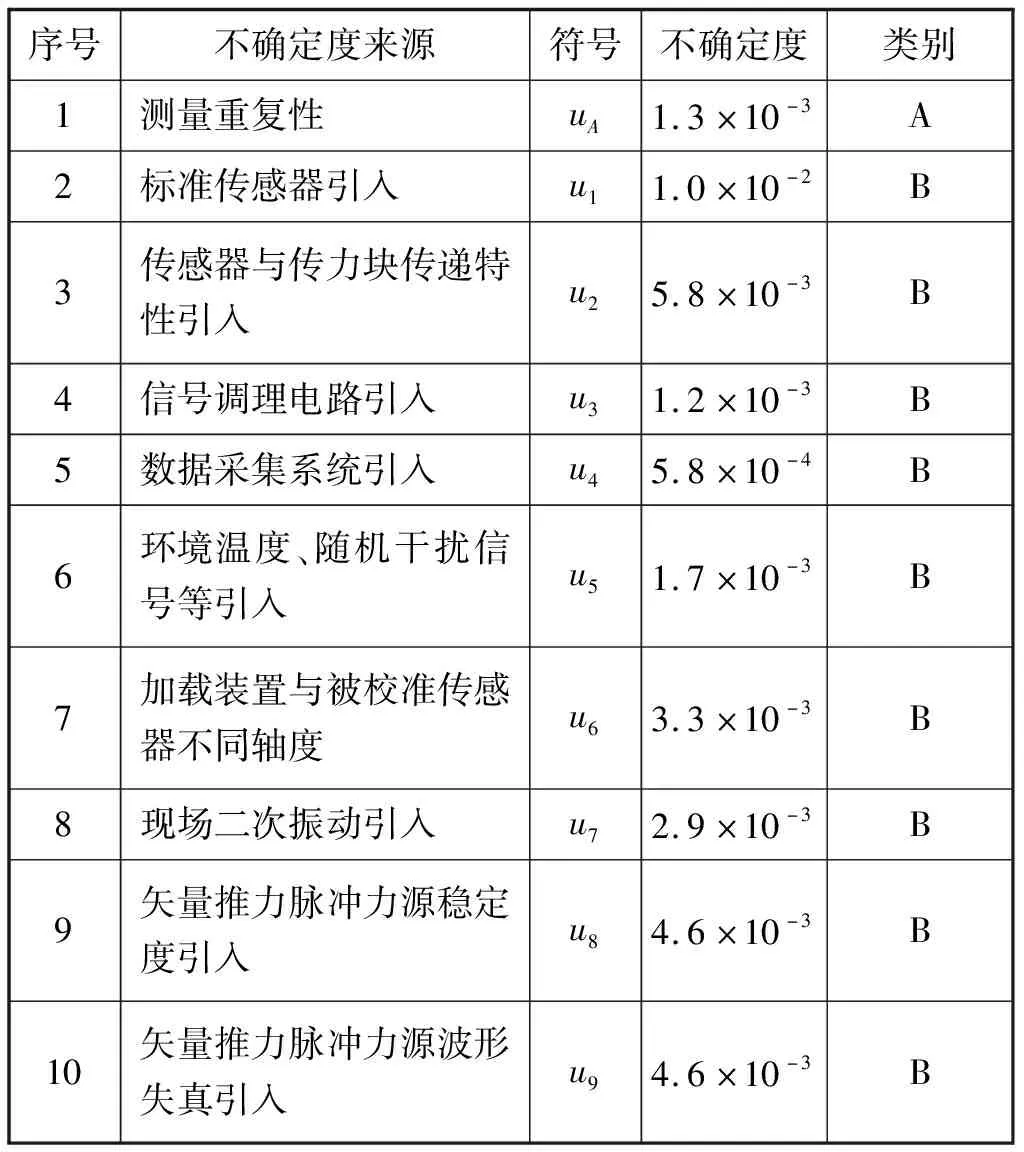
表1 試車臺矢量推力測量不確定度評估表

測量不確定度合成為

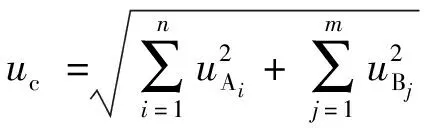
=1.5%

試車臺矢量推力校準擴展不確定度為

Urel=kuc=2×1.5%=3.0%(k=2)

5 結束語

針對發動機試車臺矢量推力現場校準需求，重點研究了基于脈沖式力源的試車臺矢量推力校準裝置總體方案、脈沖力源及傳力塊的設計、脈沖力源的力學仿真分析、試車臺矢量推力測量不確定度評定等工作，建立了發動機試車臺矢量推力校準裝置，解決了發動機試車臺現場校準的難題。該校準技術的研究成果能夠填補國防軍工行業在發動機試車臺矢量推力現場校準領域的空白，對于科研生產有著重要的理論和應用價值。另外通過簡單的結構改造后，該項校準技術也可應用于其他行業的發動機試車臺測試校準工作，應用前景廣闊。