動壓氣浮軸承鎖緊螺母裝配應力分析與改進

張翰明，郝永勤，譚映戈，朱志剛，孫亞朋

（北京航天控制儀器研究所，北京 100039）

0 引言

動壓氣浮軸承的常見支撐結構包括柱型、半球型、錐型和球型四種[1]，其結構示意圖如圖1所示。電機高速旋轉時，氣體由轉子體和支撐軸之間的間隙泵入，形成具有一定支撐剛度的氣膜，由于氣膜厚度僅微米級，因此存在加工精度高、裝配難度大、可靠性差等問題[2]。本文研究的目的是通過應力分析改進軸承結構，從而提高工作可靠性。

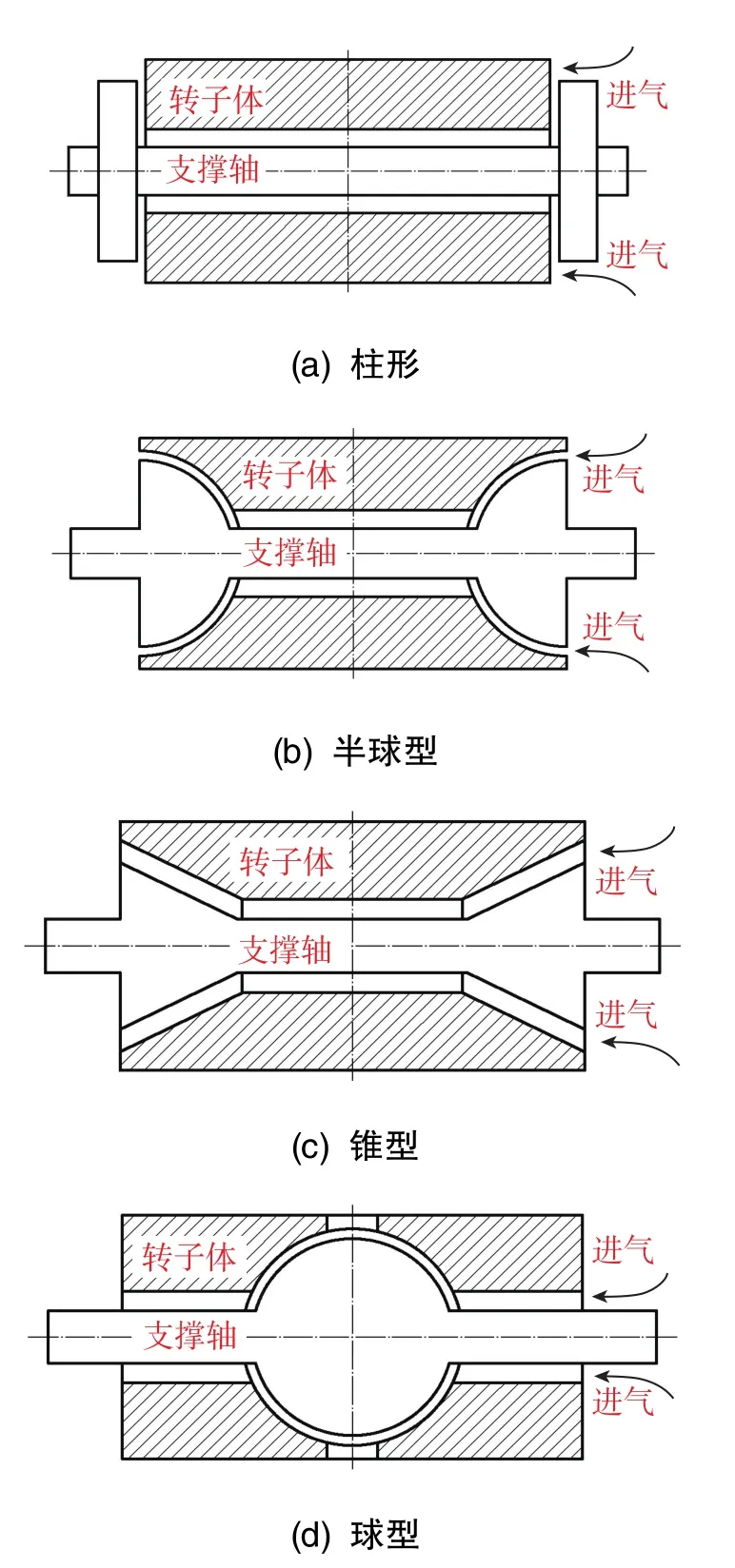
圖1 動壓氣浮軸承常見類型Fig.1 Common types of gas-dynamic bearing

提高動壓氣浮軸承工作可靠性的重點在于對鍍膜、刻槽、研磨、測試等關鍵工藝的突破。陳白帆等[3]分析了零件表面微觀工藝特征對軸承工作可靠性的影響，并提出了改善制造工藝設計的思路。王曉瑜等[4]分析了研具對零件成型精度的影響，提出了研具設計準則，并通過試驗驗證了設計方法的正確性。王京鋒等[5]提出了以反力矩測試曲線作為可靠性篩選的手段，并分析了反力矩測試曲線的原理和方法。任同群等[6]研制了軸承間隙自動測量設備，詳細介紹了設計方案和工作原理，實驗證明了綜合測量精度優于0.3μm。劉晶石[7]研究了幾種常見裝配誤差與干擾力矩的關系，提出了減小裝配誤差的合理化參數。

目前，在關鍵工藝研究中對裝配應力的研究還比較少。生產中發現，若軸承鎖緊螺母的預緊力不足，在振動、沖擊等過載測試中螺母容易出現松動，使軸承間隙發生變化、轉子震蕩增加，嚴重情況下可能導致電機失步；若螺母預緊力過大，則會導致球面變形，軸承間隙同樣會發生變化[8]。因此，要綜合考慮螺母預緊力對軸承性能的影響，既要控制半球變形，又要保證過載條件下不松動[9]。針對半球型氣浮軸承裝配應力導致球面變形的問題，本文首先通過建立螺紋連接簡化模型分析預緊力傳遞關系，然后利用有限元仿真軟件得到半球零件圓度變化，并通過實驗驗證仿真結果，最后提出有利于提高工作可靠性的結構改進方案。

1 螺紋連接的預緊力分析

如圖2所示，半球通過軸端螺母固定，將螺紋簡化為圍繞圓柱的斜面，將螺紋連接面展開為由斜面和滑塊組成的簡化模型[10]，分析螺紋連接的三個過程。

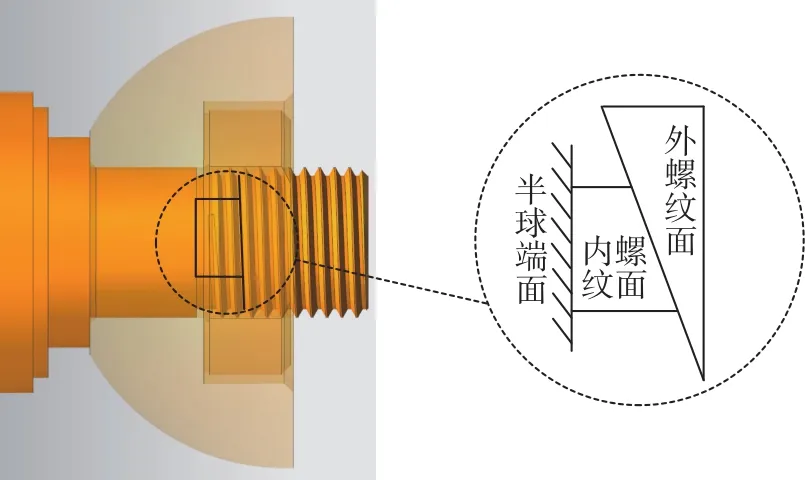
圖2 螺紋連接簡化模型Fig.2 Simplified model of threaded connection

（1）緊螺母過程

如圖3所示，螺母端面與半球端面接觸后產生擠壓，即預緊力FQ；內外螺紋間存在沿斜面上升趨勢V，外螺紋對內螺紋產生法向壓力FN和摩擦阻力μWFN，合成總反力FR；擰緊過程中扳手力矩需要同時克服螺紋接觸面間的摩擦阻力μWFN和半球端面對螺母端面的摩擦阻力Fd， 存在關系式

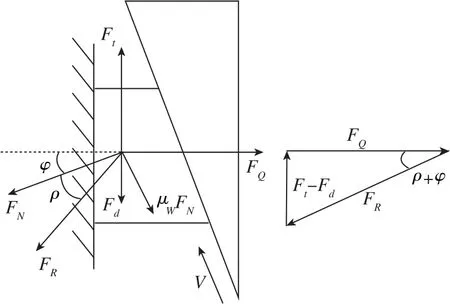
圖3 緊螺母受力關系示意圖Fig.3 Schematic diagram of locknut force relationship

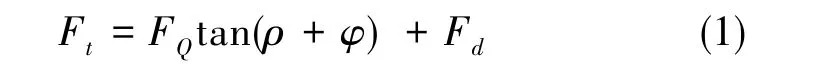
式（1）中，Ft為旋轉螺母的水平推力，ρ為FR與FN之間的夾角（當量摩擦角），φ為螺紋升角。

（2）自鎖過程

如圖4所示，釋去扳手力矩后螺母停留在原處，此時螺母存在沿斜面下滑趨勢V，螺紋接觸面間產生與運動趨勢反向的摩擦阻力μWFN，法向壓力FN與μWFN合成總反力FR，FR與預緊力FQ合成對螺母的推力Ft，維持螺母不松動。當ρ＞φ時，達到自鎖狀態。

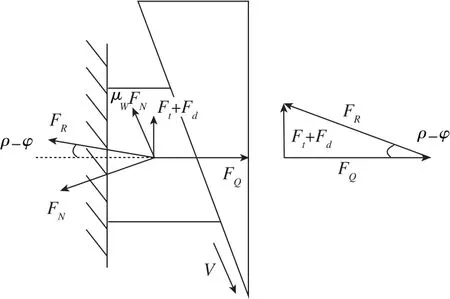
圖4 自鎖受力關系示意圖Fig.4 Schematic diagram of self-locking force relationship

（3）松螺母過程

如圖5所示，松螺母時扳手力矩要同時克服螺紋接觸面間的摩擦阻力μWFN和螺母端面對半球端面的摩擦阻力Fd， 松螺母瞬間靜摩擦轉變為動摩擦，松螺母瞬間按靜摩擦計算，存在關系式

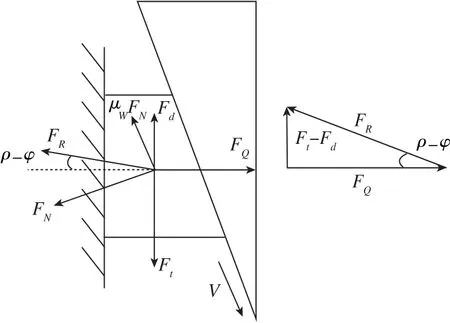
圖5 松螺母受力關系示意圖Fig.5 Schematic diagram of loosenut force relationship

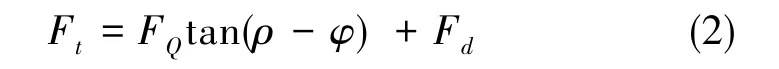
考慮到螺母端面的摩擦阻力Fd， 松螺母時扳手施加的合力矩為

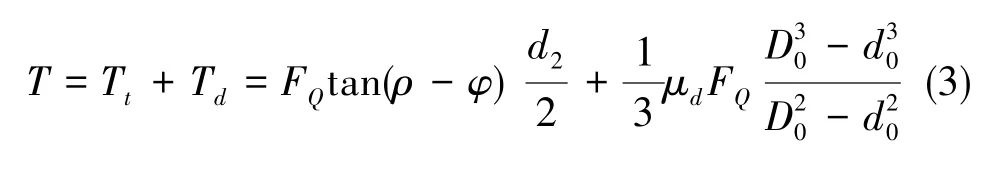
通過測量扳手力矩值可以推算螺紋預緊力，實測得松螺母力矩在60N·cm～70N·cm之間。計算中假定螺母端面與半球端面摩擦系數μd=0.1、當量摩擦角ρ=6°，由圖紙得到螺紋中徑、螺紋升角、螺母外徑等尺寸參數，計算緊螺母力矩20N·cm～70N·cm范圍內對應的預緊力值如表1所示。后續將預緊力值作為輸入載荷，研究不同預緊力作用下的半球結構變形。

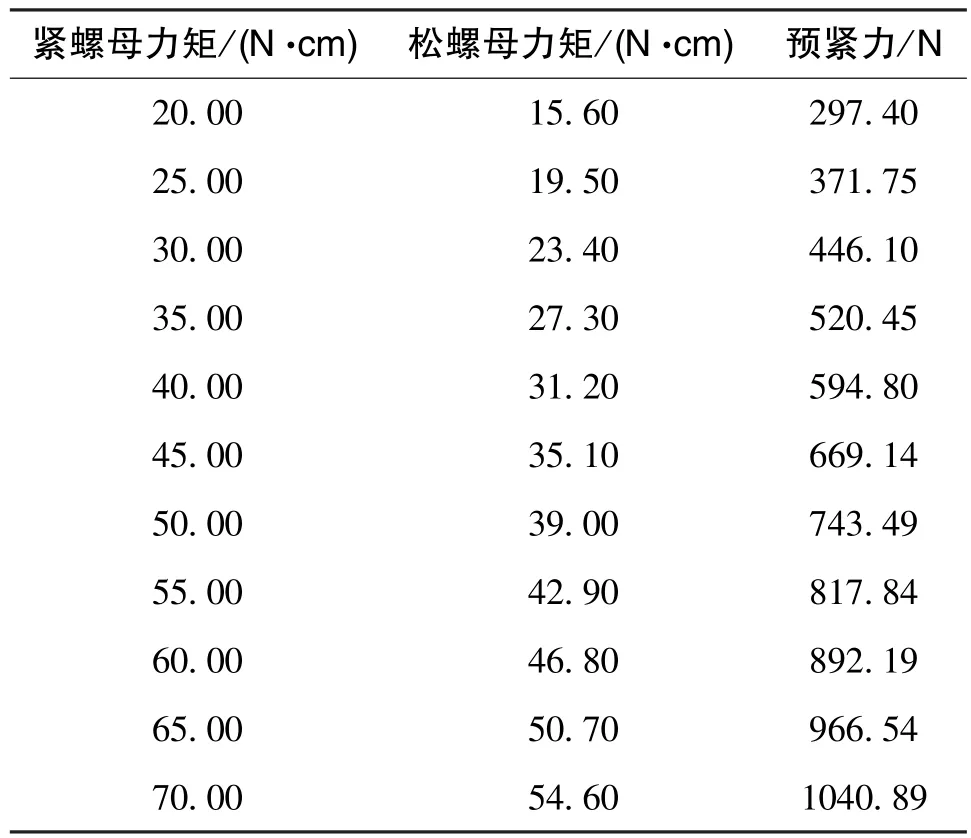
表1 螺母力矩與預緊力的關系Table 1 Relationship between torque and preload of nut

2 有限元模型建立

半球型動壓氣浮軸承為對稱結構，為簡化計算，建立由單個半球、螺母和半軸組成的三維模型，導入ANSYS Workbench進行結構靜力學分析。定義材料屬性如表2所示，模型約束與載荷條件如圖6所示，模型網格劃分質量如圖7所示。

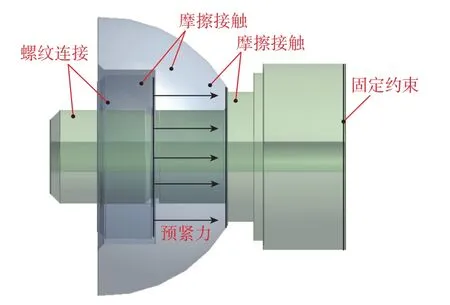
圖6 模型約束與載荷條件示意圖Fig.6 Diagram of boundary conditions and load of the model

圖7 網格劃分質量示意圖Fig.7 Diagram of meshing quality

表2 材料屬性Table 2 Material properties

3 預緊力作用下的軸承結構變形

3.1 支撐軸的變形

支撐軸的軸肩與半球小端面貼合，在螺母預緊力作用下產生擠壓變形，螺母預緊力743.49N作用下的軸肩應力分布如圖8所示。半球小端面與軸肩貼合面積為15.57mm2，理論計算應力為47.75MPa，圖8中軸肩接觸面應力值集中在36.07MPa～50.50MPa之間，與理論計算基本一致。

圖8 軸肩應力分布示意圖Fig.8 Diagram of stress distribution on shaft shoulder

在743.49N預緊力作用下支撐軸Z向（軸向）的位移變化如圖9所示，軸肩的軸向壓縮變形集中在0.317μm～0.476μm之間。半球小端面擠壓軸肩，軸肩外圓直徑小于半球小端面外圓直徑，軸肩受到不均勻擠壓，導致軸肩靠近外圓處變形更大。

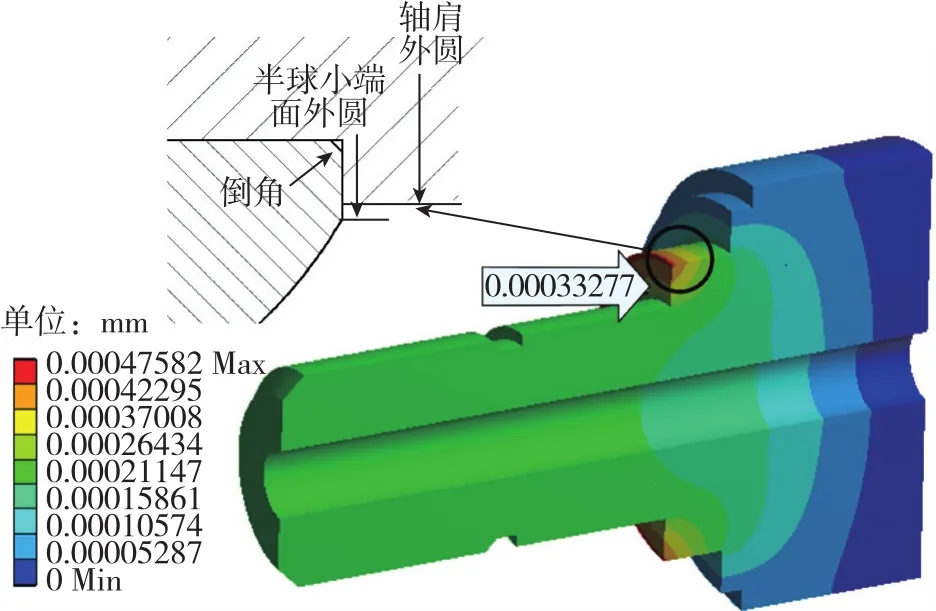
圖9 軸肩位移變化示意圖Fig.9 Diagram of displacement variation on shaft shoulder

3.2 半球的變形

半球在螺母預緊力作用下發生變形，其中的軸向變形為支撐軸變形和半球軸向變形之和。分別用兩個正交方向的輪廓母線和四個不同直徑的截面圓在受力前后的節點位移變化量表征半球整體變形情況，輪廓母線和截面圓的位置如圖10所示。X向輪廓母線指向螺母側邊的平面缺口，四個截面圓距半球大端的距離分別為0.4mm、2.4mm、4.0mm、6.6mm。

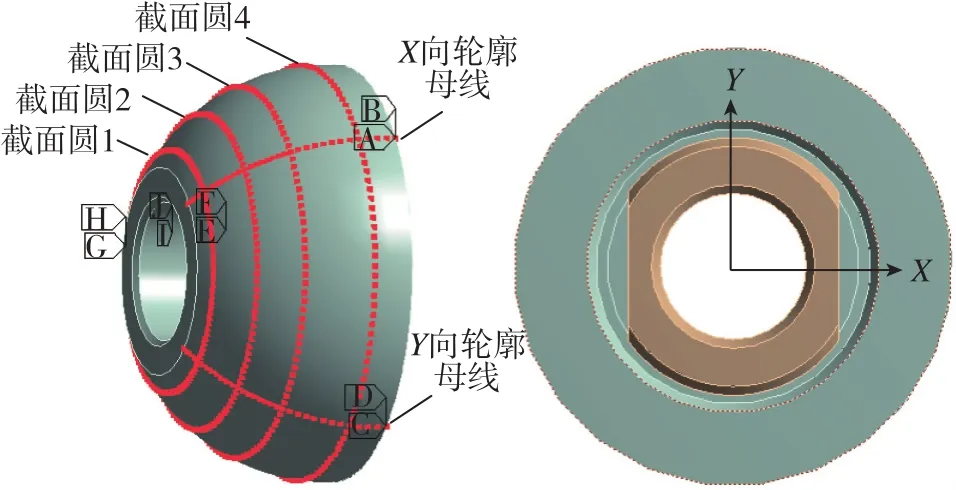
圖10 輪廓母線和截面圓位置示意圖Fig.10 Position diagram of generatrix and circular section

（1）兩條輪廓母線的節點位移

在743.49N預緊力作用下，圖10中兩條輪廓母線的軸向位移如圖11所示。兩條母線節點的軸向位移最大值均出現在中間區域，螺母側邊的兩個平面對半球軸向位移有一定的影響。對比可見，X向輪廓母線的軸向位移略小于Y向輪廓母線的軸向位移。

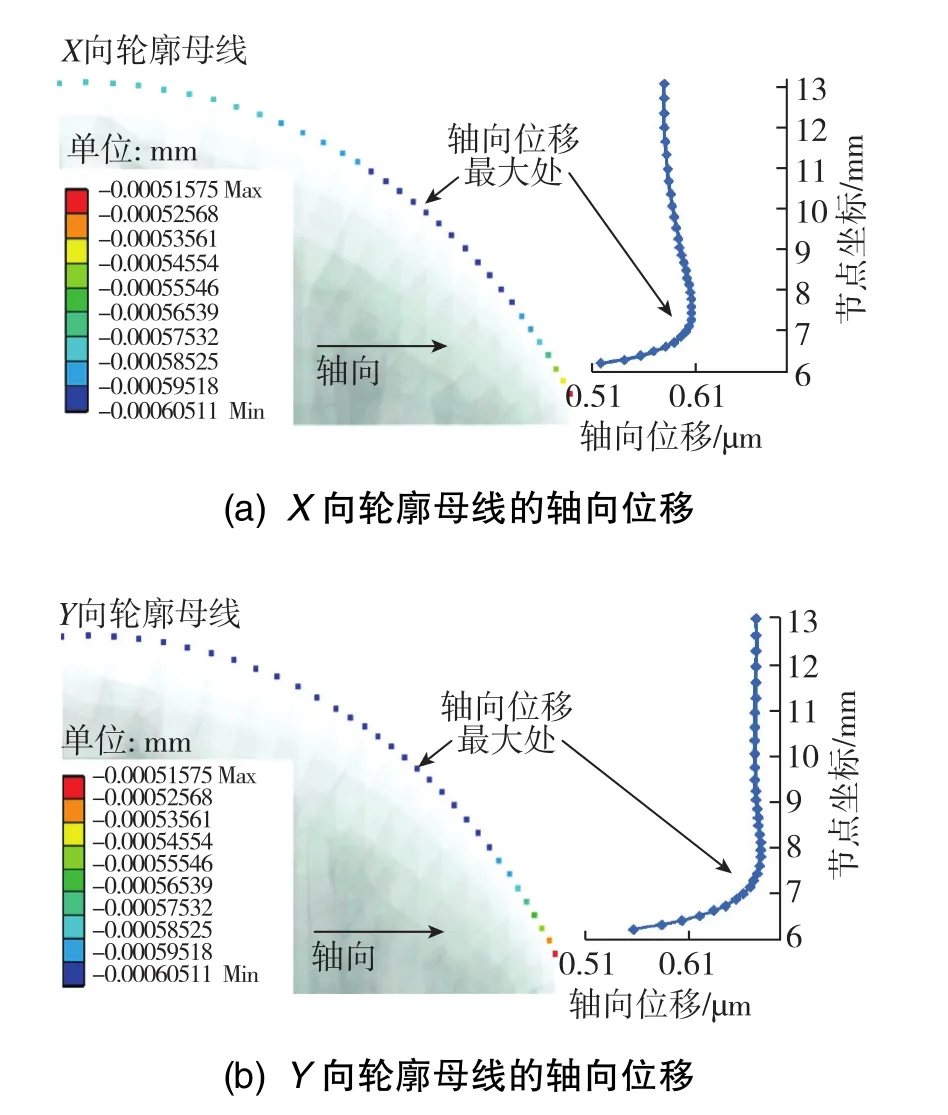
圖11 輪廓母線的軸向位移Fig.11 Axial displacement of generatrix

兩條輪廓母線的徑向位移如圖12所示。半球中間區域的徑向位移變化同樣比較明顯，位移變化量約0.02μm。X向輪廓母線在大端處徑向位移減小約0.05μm，Y向輪廓母線在大端處徑向位移增大約0.03μm，大端邊緣沿圓周方向趨于橢圓。

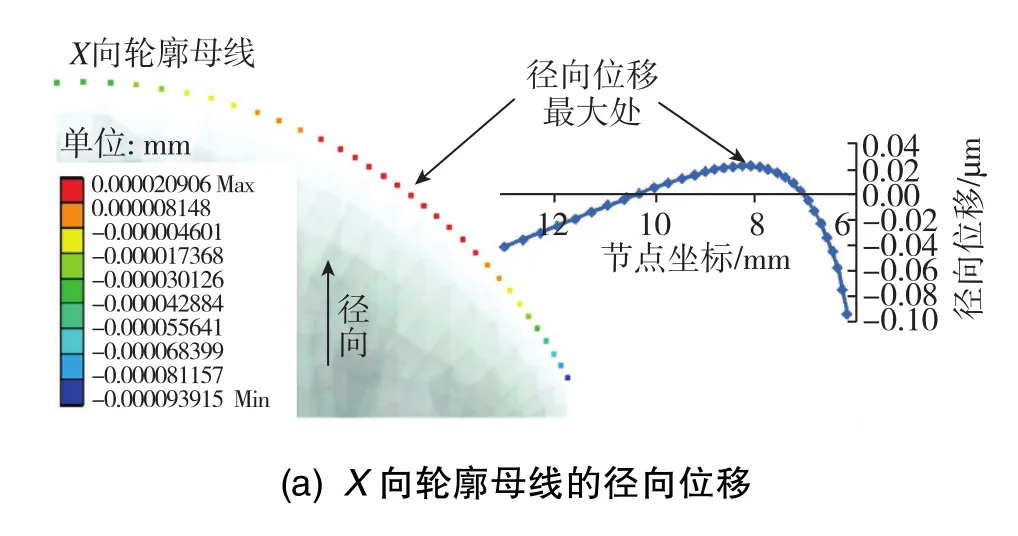
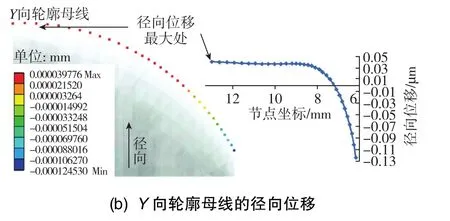
圖12 輪廓母線的徑向位移Fig.12 Radial displacement of generatrix

（2）四個截面圓的節點位移

最小二乘圓法是GB／T 7234-2004《產品幾何量技術規范（GPS）圓度測量——術語、定義及參數》中規定的4種圓度評定方法之一，該方法具有理論成熟、算法簡便的優點[11]。此處采用最小二乘圓法對比圖10中四個截面圓受743.49N預緊力前后的圓度變化，設截面圓上各節點極坐標為Pi（ri， θi）（i=1， 2， …， n）， 最小二乘圓的圓心直角坐標為G（a，b），最小二乘圓的半徑為R，計算公式為

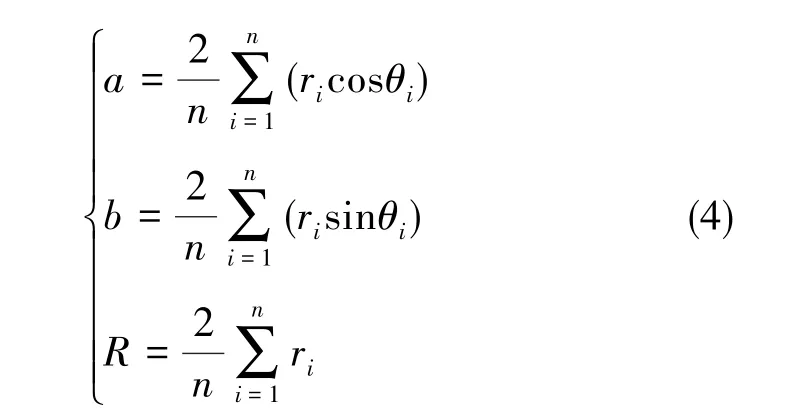
式（4）中，n為節點總數，i為節點序號。由式（4）求最小二乘圓的圓心坐標G（a， b）和半徑R，得到圓度的最小二乘評定結果為

式（5）中，Rmax、Rmin分別為截面圓上各節點到最小二乘圓心距離的最大值和最小值。根據式（4）和式（5）用Matlab編程計算圓度，結果如圖13所示，由小端至大端四個截面圓的圓度分別為0.021μm、0.021μm、 0.050μm、 0.030μm。 圖13（d）中 Y 向的徑向變形大于X向，這是由于螺母側邊的圓面對半球的擠壓大于平面，導致大端截面圓趨于橢圓。

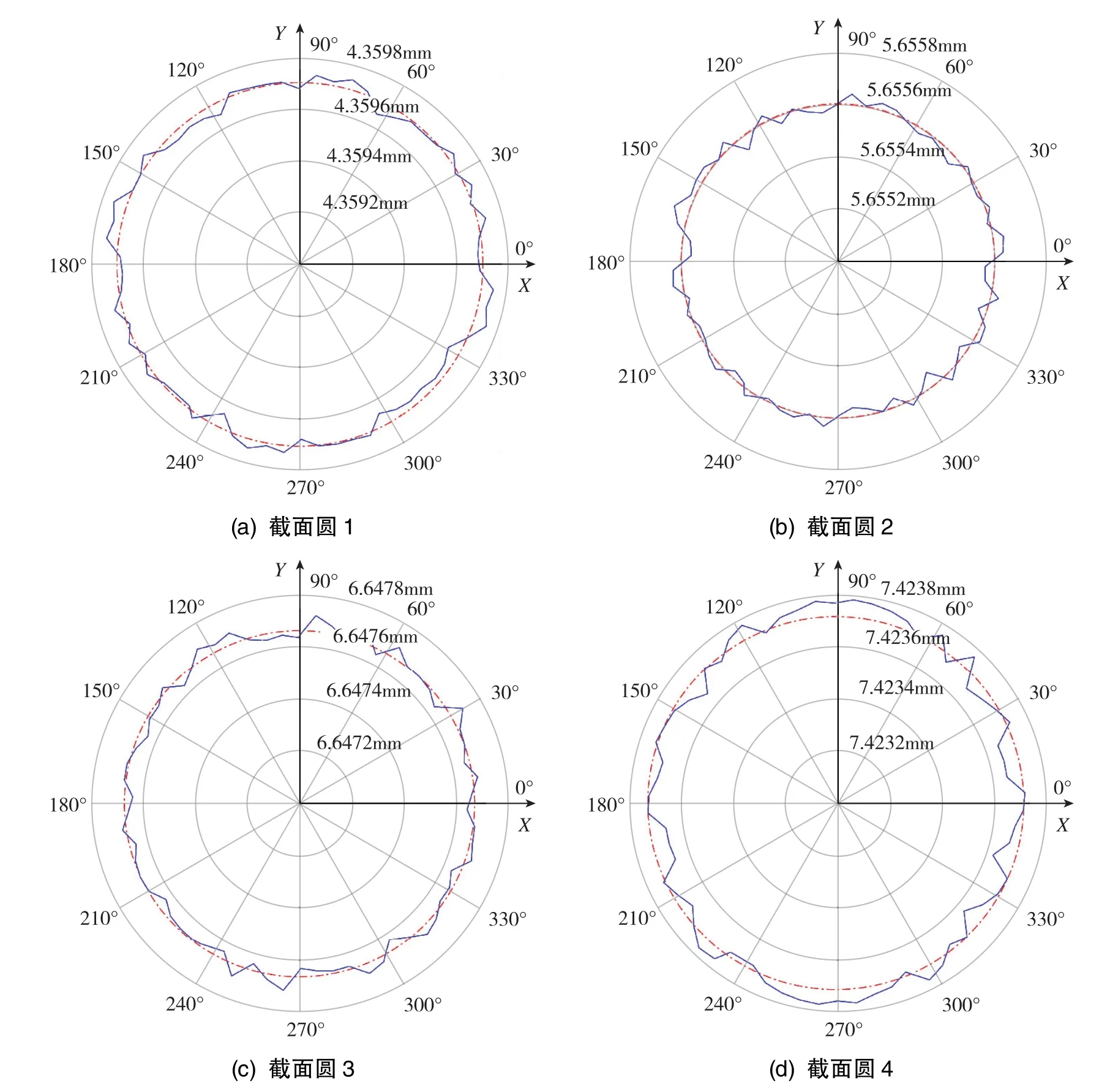
圖13 四個截面圓的圓度Fig.13 Roundness of four circular sections

為進一步說明受力后半球輪廓的變化，將節點受力后的徑向位移擴大10000倍對比受力前后截面圓的變化，具體如圖14所示。其中，藍線為受力前狀態，紅線為受力后狀態，小端的截面圓1受力后沿徑向收縮，中間的截面圓2和截面圓3受力后沿徑向擴大，大端的截面圓4受力后趨于橢圓，這表明半球大端更容易受預緊力影響導致圓度下降。

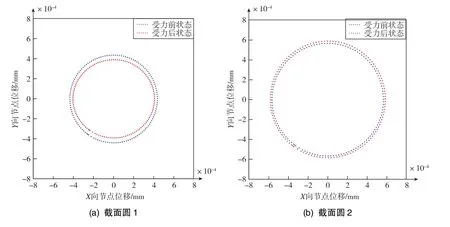
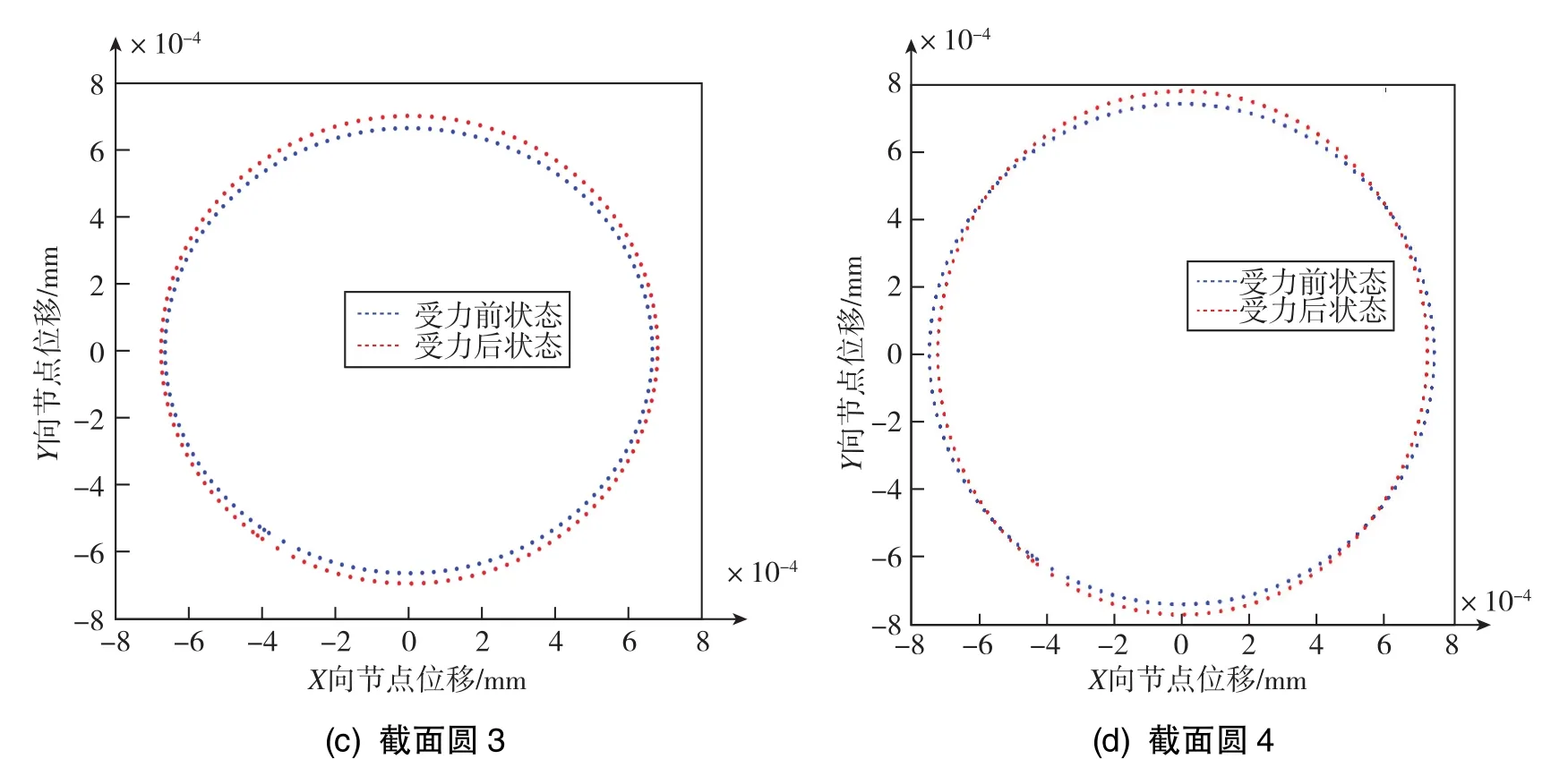
圖14 四截面圓受力前后徑向變形對比Fig.14 Comparison of radial deformation of four circular sections before and after stress

3.3 螺母力矩和圓度誤差的測量實驗

國內外通用的螺栓預緊力測量方法有扭矩扳手法、電阻應變片法、光彈法和磁敏電阻法[12]。扭矩扳手法操作簡便，在裝配生產線中得到廣泛應用，但是要保證螺紋具有較高的加工精度和較好的潤滑條件[13]。電阻應變片法能夠直接測量被連接件接觸面間的壓應力，是一種精度較高的測量方法。光彈法用透明材料制作零件模型，模擬實際受力狀態，是實驗室測量方法。磁敏電阻法抗干擾能力強，適合在惡劣環境中應用，但精度不高。

半球與軸肩的接觸面積僅為15.57mm2，很難通過電阻應變片直接測量。根據上述螺紋連接的預緊力分析可知，螺母預緊力可依據松螺母或緊螺母力矩計算得到，其中的螺紋中徑、升角、外徑、軸孔直徑是確定值，摩擦系數、當量摩擦角與材料屬性、加工精度、潤滑條件有關。在難以測定鈹材和中密度合金之間摩擦系數的情況下，參考同種鋼材料的靜摩擦系數對μd取值，并通過測量螺母力矩驗證取值合理性。

采用數顯扭力矩螺絲刀測量松螺母和緊螺母力矩，在20N·cm～70N·cm范圍內測量6組數據，測量結果與計算結果數據對比如圖15所示，兩組數據均線性增加，偏離度較小。實驗表明，摩擦系數和當量摩擦角選取合理，能夠反映螺母的實際受力情況。另一方面，使用形狀測量儀測量圖9所示四個截面圓的圓度，測量實驗如圖16所示，所得測量值與仿真值對比如表3所示，測量值略大于仿真值，相差約0.01μm。

圖15 螺母力矩計算與測量結果對比Fig.15 Comparison between calculating and measuring results of nut torque

圖16 圓度測量實驗Fig.16 Diagram of roundness measurement experiment

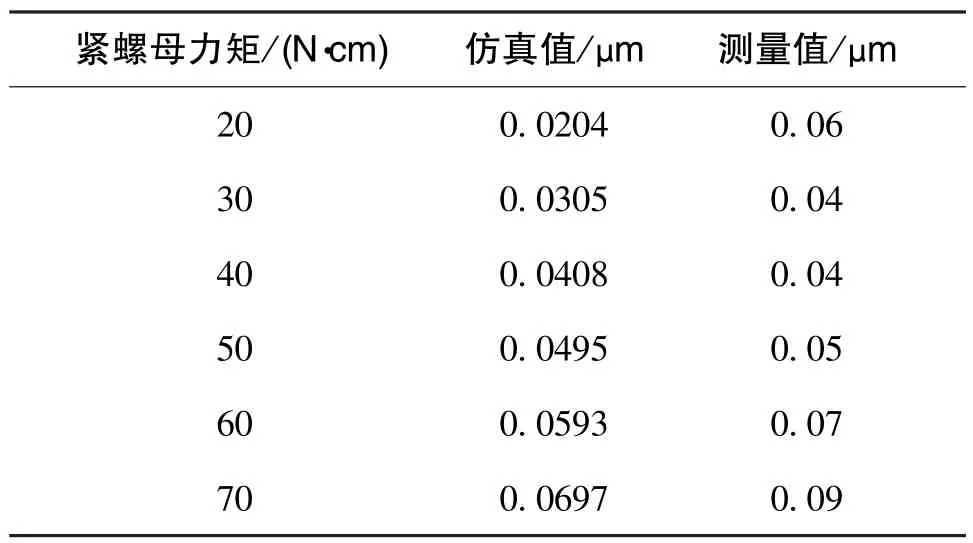
表3 圓度測量值與仿真值對比Table 3 Comparison between measuring and simulating results of roundness

4 鎖緊螺母的結構改進

以上分析表明，半球與螺母之間的接觸面為非圓面會導致半球受擠壓后趨于橢圓，為此提出鎖緊螺母結構改進方案，結構改進前后的對比如圖17所示。

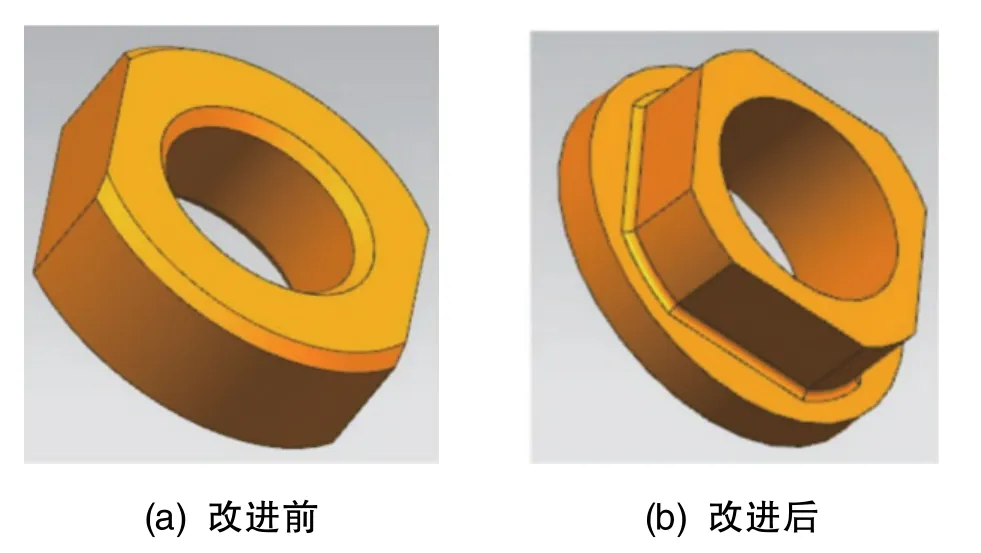
圖17 螺母結構改進前后對比Fig.17 Comparison of nut structure before and after optimization

改進后螺母與半球接觸面變為圓面，將圖6模型中的螺母替換為圖17（b）中的圓螺母，約束與載荷條件不變。兩種螺母結構在同時產生743.49N預緊力時的整體變形云圖如圖18所示，其中的支撐軸被隱藏。圖18（a）中的半球面圓周方向變形不均勻，球面輪廓處取兩節點，位移約1.1μm，裝配后表現為半球截面的圓度下降；圖18（b）中的半球面圓周方向變形均勻，球面輪廓處取兩節點，位移約0.99μm，主要變形是半球受到擠壓后產生的軸向壓縮和徑向膨脹。由此可見，改進后螺母預緊力對半球圓度影響減小。

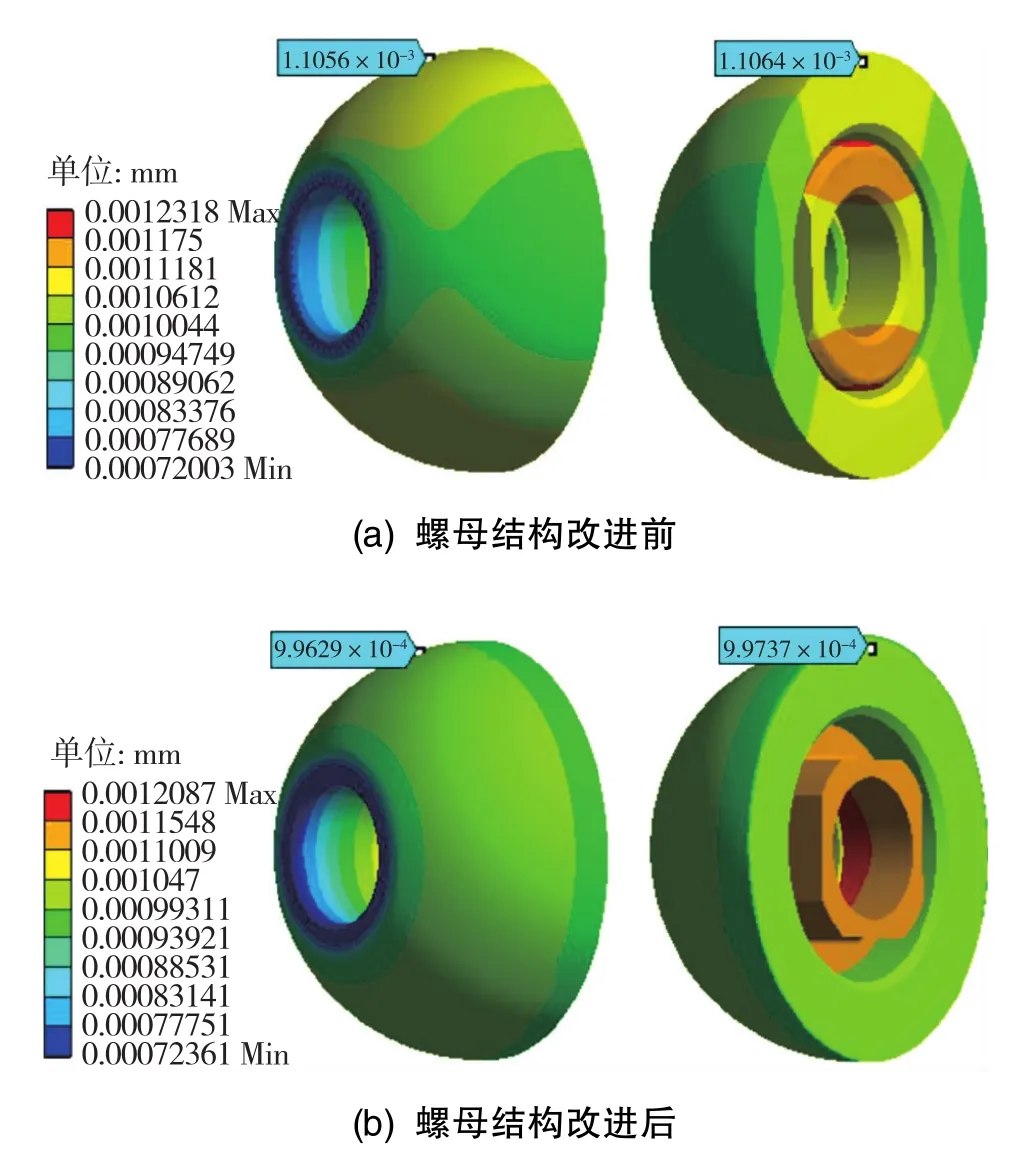
圖18 螺母結構改進前后的變形云圖Fig.18 Deformation nephogram of nut structure before and after optimization

5 結論

動壓氣浮軸承是支撐微小型電機高速旋轉的重要組件，在半球零件起停過程中容易受到磨損，是影響可靠性的薄弱環節。在保證加工精度的同時，從裝配應力角度研究螺紋緊固件在預緊后的變形分布，通過結構改進消除不利影響，對生產實際具有指導作用。研究得出以下結論：

1）通過建立螺紋連接結構簡化模型，將螺紋緊固過程細化為緊螺母、自鎖、松螺母三個階段，分析扭力矩與螺母預緊力之間的轉化關系，為有限元仿真中螺紋連接結構的載荷輸入提供依據。

2）通過建立氣浮軸承結構靜力學模型，得到球面母線節點和截面圓節點在不同受力狀態下的節點位移，體現了半球形貌變化。

3）在有限元分析基礎上改進氣浮軸承鎖緊螺母結構，改進后的半球沿圓周變形更加均勻，螺母預緊力對半球圓度影響減小，裝配應變分布更加合理。