海底地形匹配高效質點濾波導航方法

馬 騰，丁碩碩，范佳佳，李 曄

（1.哈爾濱工程大學 水下機器人技術國家級重點實驗室，黑龍江 哈爾濱 150001；2.哈爾濱理工大學 自動化學院，黑龍江 哈爾濱 150001）

0 引言

自主水下機器人（Autonomous Underwater Vehicle，AUV）是執行海底礦物勘探、水下管道檢測、海洋環境調查等任務的重要載體平臺[1]。AUV能否高效、精確地執行海底勘探等任務取決于其導航精度[2]。在傳統導航方法中，由于無線電訊號在水下衰減嚴重，全球定位系統（Global Positioning System，GPS）無法在AUV水下航行時為其提供精確定位信息。慣性導航系統（Inertial Navigation System，INS）不僅需要價格昂貴的多普勒計程儀（Doppler Velocity Log，DVL）和航姿參考系統（Attitude and Heading Reference System，AHRS）輔助，其導航誤差累積特性也導致其難以作為AUV長時間水下航行的精確導航手段[3]。長基線（Long Baseline，LBL）、超短基線（Ultrashort Baseline，USBL）等聲學導航手段可在AUV水下航行過程中提供具備有界誤差的精確導航結果。但LBL聲學導航需要提前于海底布設多個聲信標，使用USBL實現精確導航則需要AUV保持同支持母船的通訊，兩者均使AUV作業范圍受限嚴重[4]。海底地形匹配導航等地球物理導航手段，不依賴于衛星、聲學信標或支持母船等外部輔助，不存在累積誤差，可實現AUV長時間、全天候、遠距離精確導航，已經得到了世界各國研究人員的廣泛重視[5]。

目前，國內外研究人員已利用多波束測深探測儀（Multibeam Echosounder，MBES）針對海底地形匹配導航方法展開大量理論和試驗研究[6-7]。海底地形匹配導航最早是通過卡爾曼濾波（Kalman Filter，KF）[8]、擴展卡爾曼濾波（Extended Kalman Filter，EKF）[9]、無跡卡爾曼濾波（Unscented Kalman Filter，UKF）[10]等參數濾波方法展開的。與傳統KF方法中以觀測到的水深值為測量更新不同，Li Peijua[8]等提出將迭代最近輪廓點（Iterated Closest Contour Point，ICCP）匹配結果與INS定位結果差值作為KF測量值，然后通過濾波器反饋校正及時校正SINS的累積誤差。

隨著計算機技術和非線性優化技術的不斷進步，粒子濾波器（Particle Filter，PF）、質點濾波器（Point-Mass Filter，PMF）逐漸成為海底地形匹配導航問題的重要解決方案。Jind?ich Duník[11]等提出通過 RaoBlackwellized質點濾波器解決海底地形匹配導航問題，其通過回放式仿真試驗驗證質點濾波器在解決地形匹配導航問題時具備較高精度，對質點初始化結果有極強魯棒性，計算復雜度較小且可通過理論推導預測。Georgios Salavasidis[12]等提出以聲學高度計為地形獲取手段，通過PF方法實現為期77小時的AUV長航程精確水下導航。周天[13]等在用于海底地形匹配導航的PF 中引入了變柵格尺寸的KLD（Kullback–Leibler distance）方法，極大降低了算法運行所需的資源消耗。針對MBES測量過程中存在的地形畸變現象，Peng Dongdong[14]等提出利用Huber損失函數修改粒子權重計算方程，從而在重采樣過程中減少離群值對估計值的影響。

由于具備對非高斯噪聲和非線性運動模型的出色擬合能力，粒子濾波和質點濾波技術逐漸成為海底地形匹配導航方法研究的主流，而考慮 AUV機載計算機數據處理能力受限，質點濾波在海底地形匹配導航中具備更強的實用性。但如圖1所示，MBES測繪得到的海底地形測點空間分布不規則，而先驗地圖則往往是網格化柵格數據，導致在質點權重計算過程中，實測地形測點與先驗數據對應關系計算中存在大量插值過程，造成極大計算消耗。

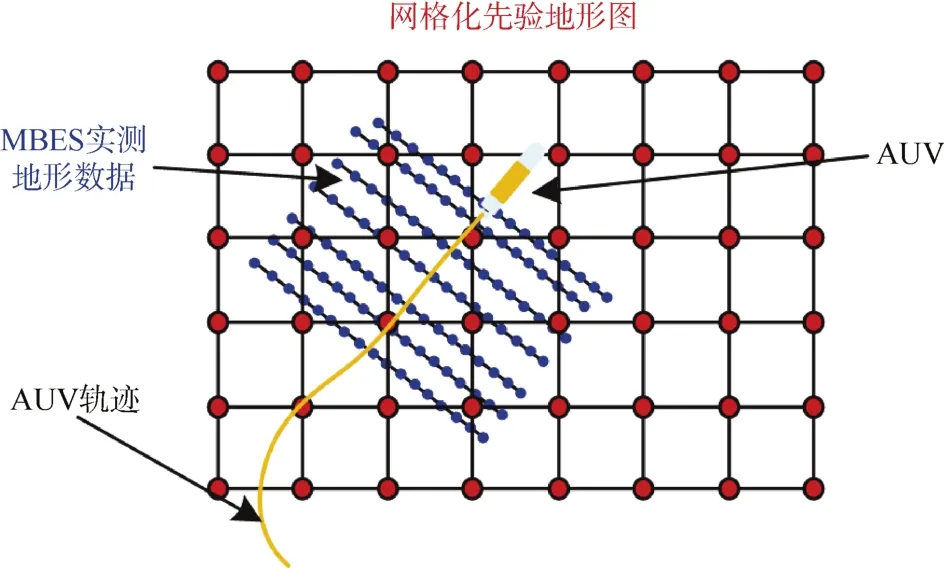
圖1 先驗地形圖與MBES實測地形數據Fig.1 A priori bathymetric map and bathymetric data measured using a MBES

為實現AUV的實時海底地形匹配精確導航，本文設計了一種海底地形匹配高效質點濾波導航方法。本文提出通過構建偽輸入高斯過程（Sparse Pseudo-input Gaussian Processes，SPGPs）模型實現對海底地形深度的高效、準確估計，從而將MBES實時測繪地形數據網格化形成概率地圖；提出適用于概率地圖的質點權重計算模型，并完成了基于概率地圖的海底地形匹配質點濾波算法框架設計。最后，通過船載MBES采集的海試數據，對所提出的基于 SPGPs的測深數據網格化方法和海底地形匹配質點濾波方法進行了回放式仿真數據驗證。

1 測深數據網格化概率地圖構建方法

實測海底地形數據的網格化是質點濾波器中最為耗時的過程。傳統網格化方法包括反距離加權（Inverse Distance Weighted，IDW）插值[15]、克里金（Kriging）插值法[16]等，其中，IDW 插值忽略了地形測點之間的相關性關系，導致插值結果誤差嚴重，而Kriging插值法雖然考慮了地形測點相關性，但其計算結構較IDW插值法更為復雜，計算效率較低。

本文提出通過 SPGPs回歸方法實現網格化插值。SPGPs回歸方法其實質是利用少量偽輸入點代替全部歷史數據實現高斯過程（Gaussian Process，GP）回歸中的 GP模型訓練[17]。因而本文首先對GP回歸在網格化插值中的應用進行介紹。

GP模型可以看作一個輸入為歷史地形測深數據、輸出為多元高斯分布均值和方差的函數。換而言之，在包含N個地形測點的海底地形測深數據集中，假設N個測點的平面坐標和深度分別為和，則可將其視為無限維度中從1個N變量高斯分布中取樣的單點，即N個測點的深度總是滿足1個聯合高斯分布N(μ,Σ)，其中μ和 Σ 分別為高斯分布的均值和方差。在GP模型中，由于地形測深數據輸入前會減去其地形深度均值，通常取μ=0，而Σ則由N個測點間相關性計算得到，且與測點水平位置的差值成正相關。

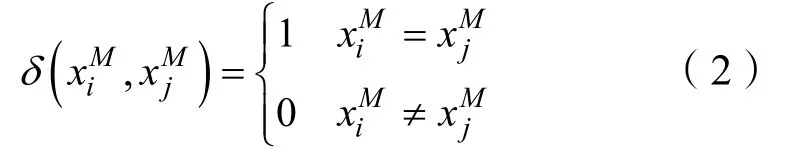
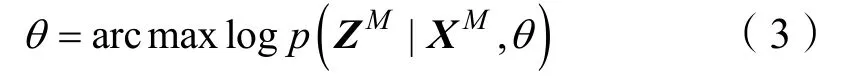
實現，該計算可以通過Gauss-Newton方法實現。

完成GP模型構建后，利用該模型實現網格點地形高程插值。假設網格點水平坐標為x*，其水深值z*滿足以下多元高斯分布：

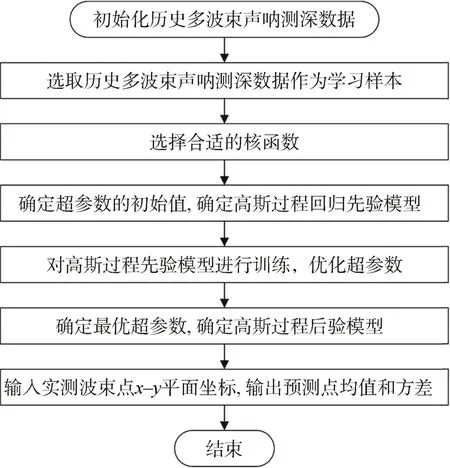
圖2 高斯過程回歸的地形水深估計流程圖Fig.2 Flowchart of terrain depth estimate using the GP regression method

考慮采用全部歷史MBES測深數據訓練GP模型會造成巨量計算消耗，在GP回歸算法的基礎上，本文提出在全部歷史 MBES測深數據中提取能夠保留大部分信息的少量偽輸入點，通過偽輸入點訓練 SPGPs模型，從而實現測深數據的高效網格化操作。

假設M個偽輸入點（M遠小于N）水平面坐標為，則通過最大化邊緣概率：

即可同時求取X′和超參數θ。式（9）中，j?[1,M]；IN為大小為N×N的單位矩陣；Λ=diag(λ)且λ={λ1,λ2,...,λN}，其中，。

在通過Gauss-Newton方法求解式（9）后，水平坐標為x*的網格插值點水深值z*滿足均值為*μ，均值為Σ*的高斯分布，且：

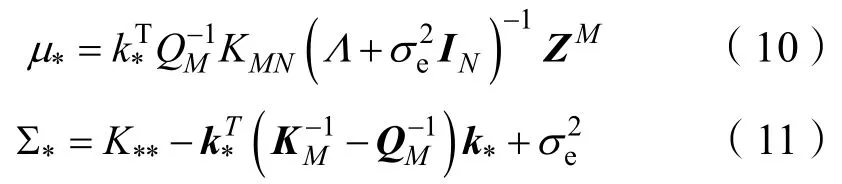
式（10）和式（11）中：

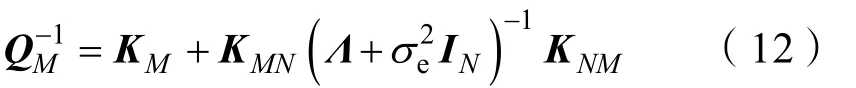
2 質點濾波算法

本文所設計的海底地形匹配質點濾波算法框架如圖3所示。

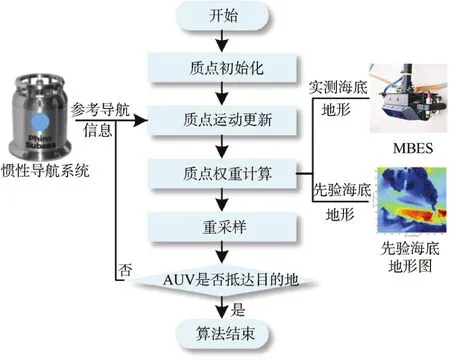
圖3 質點濾波算法框架Fig.3 Framework of point-mass filter algorithm

傳統質點濾波中通過計算MSD（Mean Square Displacement）算子實現質點權重計算。假設質點i在t時刻大小為N1×N2的網格化地圖實測水深表示為h′(i,j)(i=1,2,...,N1,j=1,2,...,N2)，對應位置的先驗地形圖水深值為h(i,j)，則其質點i權重wi為

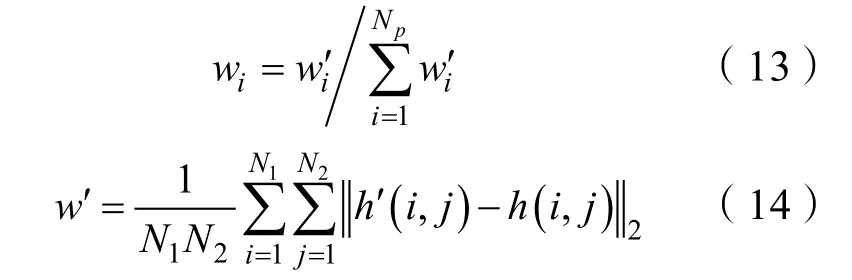
但是，以上方法忽略了實測地圖網格化過程中不同網格節點的置信度差別。如式（11）所示，SPGPs回歸方法的一大優勢在于其可以在網格化插值過程中構建概率地圖，即對各個插值節點的方差Σi,j進行估計。因而本文提出一種適用于概率地圖的質點權重計算方法，即將式（14）改寫為

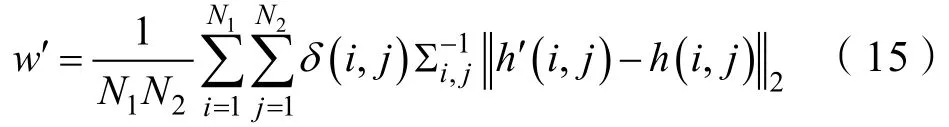
式中，克羅內克函數δ(i,j)為

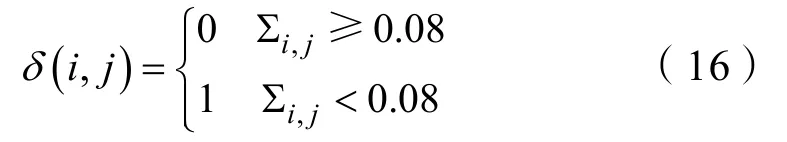
3 回放式仿真試驗

如圖4所示，于青島中沙礁海域開展了船載MBES的數據獲取海上試驗。試驗載體船與設備布置如圖5所示。

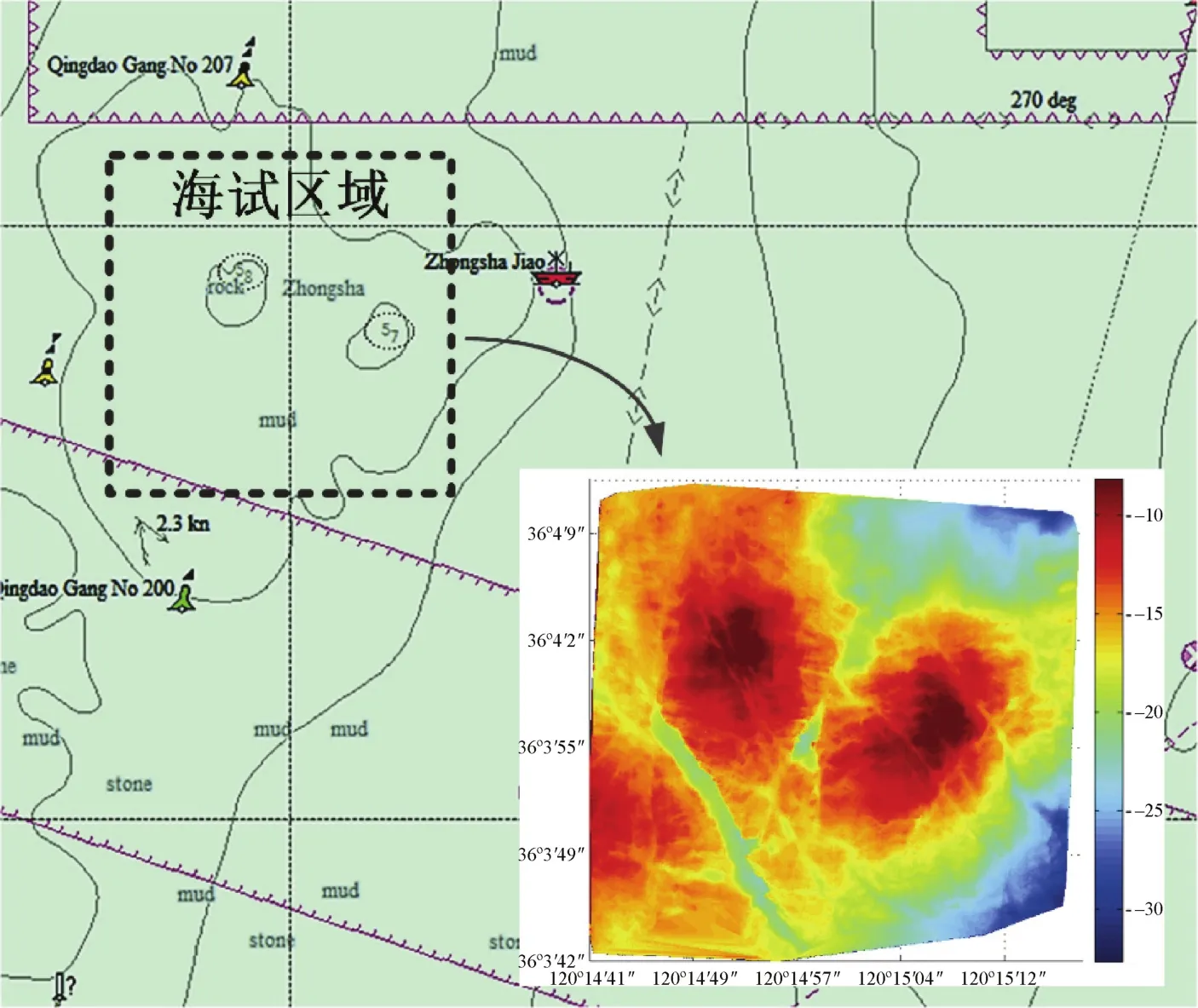
圖4 海試試驗區域Fig.4 Sea trial area

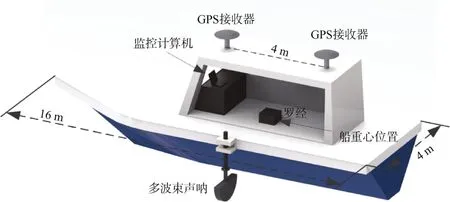
圖5 試驗船只與設備布置Fig.5 Experimental vessel and equipment layout

如圖6所示，試驗使用T–sea CMBS200在線MBES作為海底地形數據測繪設備。T–sea CMBS200每次發射192個聲學脈沖信號，測線寬度約為MBES距海底距離的10倍，水平波束寬度優于1°，垂直波束開角優于 2°，水平視場角≥140°，測距離≥300 m，距離分辨率優于2 cm，作業頻率為4 Hz。試驗過程中載體運動狀態信息由圖 7所示的StarNeto XW–GI5651導航系統給出，在GPS信號輔助下，該系統艏向角測量誤差優于0.1°，橫傾、縱傾角測量誤差優于 0.01°，水平面定位誤差小于1 m，作業頻率為10 Hz。

圖6 T–sea CMBS200在線多波束聲吶Fig.6 T-sea CMBS200 online MBES

圖7 StarNeto XW–GI5651導航系統Fig.7 StarNeto XW-GI5651 navigation system

采用海上試驗數據開展回放式仿真試驗。軌跡長度約為1 800 m，載體航速約為4 kn，數據更新頻率為4 Hz，以GPS軌跡作為真實軌跡，慣性導航軌跡通過式（17）進行模擬。

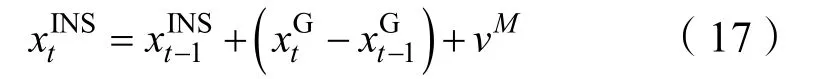
在軌跡上每隔25 s選取1個地形導航點，并進行1次質點權重計算和重采樣，輸出海底地形匹配質點濾波導航結果。軌跡中共存在47個地形導航點，粒子數設定為500個，慣導系統初始誤差約為9.5 m。

如圖8所示，在第5個地形導航點后濾波器中質點分布高度收斂于載體實際位置處，質點濾波器輸出結果保持穩定。如圖9和圖10所示，海底地形匹配質點濾波導航結果與 GPS結果高度吻合，在任務過程當中的47個地形導航點上，慣性導航系統和本文提出的地形匹配導航系統提供的 AUV定位誤差均值分別為25.39 m和1.46 m，中位數分別為26.38 m和1.26 m。算法在MATLAB平臺下執行耗時為69.63 s，且其中53.14 s用于概率地圖構建，總耗時占任務時間比例少于8%。

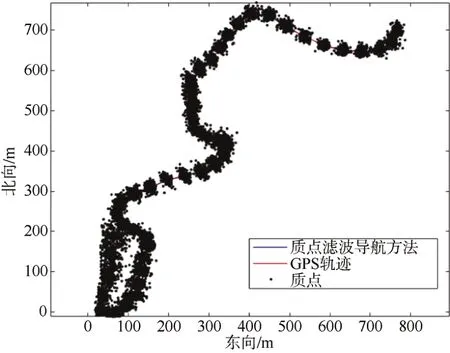
圖8 任務過程中質點分布變化Fig.8 Changes in mass point distribution during the mission

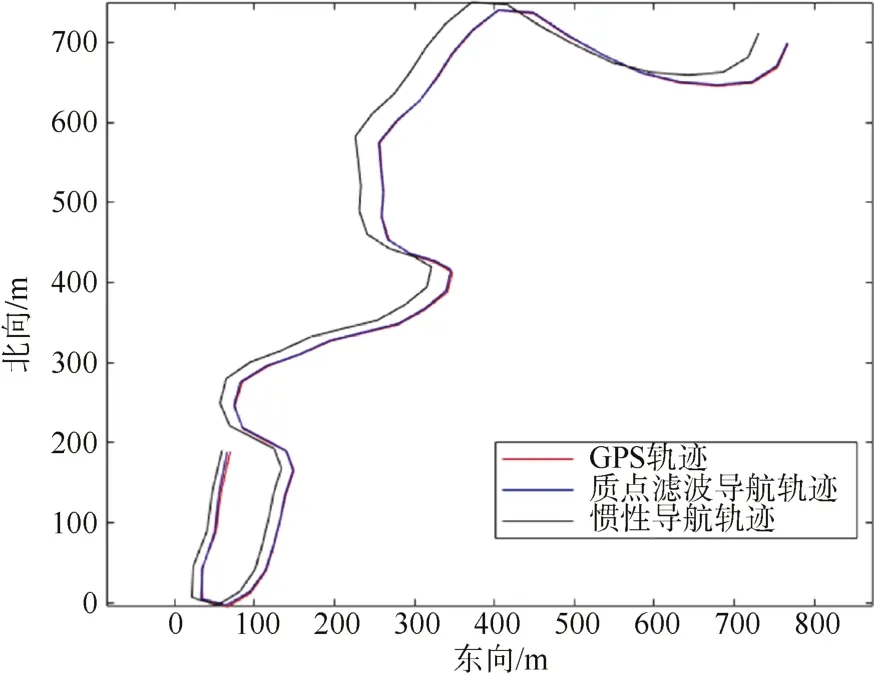
圖9 導航系統輸出軌跡結果Fig.9 Trajectories yielded by navigation systems

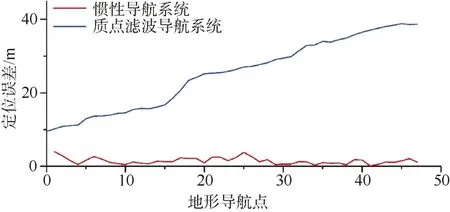
圖10 任務過程中載體定位結果Fig.10 Location errors of the vessel during the mission

試驗結果證明：所提出海底地形匹配高效質點濾波導航方法可以在低成本慣性導航系統輔助下為AUV提供在線的精確導航信息。

4 結論

本文提出了一種海底地形匹配高效質點濾波導航算法，并通過海測數據回放式仿真試驗驗證，得到以下結論：

1）相較于IDW插值和Kriging方法，SPGPs回歸用于網格化插值可同時達到插值精度和計算效率的最優；

2）所提出海底地形匹配質點濾波導航方法可獲得精確定位結果，其實時導航圓概率誤差小于2 m；

3）所提出海底地形匹配高效質點濾波導航方法耗時遠小于任務時常，可實現 AUV在線精確導航。