雙S型輻板車輪對鋼軌波磨的影響*
張銀仙 陳光雄 楊普淼 康 熙
(西南交通大學摩擦學研究所 四川成都 610031)
鋼軌波浪形磨耗,簡稱鋼軌波磨,是指在鋼軌上與車輪接觸的表面產生的波浪形不均勻磨耗。GRASSIE等[1]結合歷年學者的研究,提出波磨的2種形成機制,即固定波長機制和損傷機制,并據其將波磨分類,總結了所有波磨類型的特征、形成原因以及緩減措施,為后續研究提供了重要參考。SATO等[2]鑒于波磨在日本盛行的現象以及波磨發生機制和對應措施的不完善,詳盡地回顧和分析了國內外學者對于鋼軌波磨的研究。金學松等[3]通過大量的文獻研究,將波磨成因理論歸納為自激振動理論、反饋振動理論和其他理論。基于自激振動理論,陳光雄等[4-5]提出的蠕滑力飽和導致系統發生摩擦自激振動從而引發鋼軌波磨的機制,可以較為完善地解釋小半徑曲線上低軌普遍發生波磨而高軌鮮有波磨的現象。文獻[6-9]對該理論模型的應用,進一步驗證了輪軌摩擦自激振動導致波磨理論的正確性。
目前,鋼軌打磨是最有效的消除波磨的措施[10]。但是,打磨這項維修工程耗時耗力,是一種非常被動的解決措施,科研人員們更傾向于從波磨形成機制出發去研究抑制或消除波磨的措施。劉學毅和印洪[11]基于輪對黏滑振動形成波磨的理論,提出將曲線段發生波磨的鋼軌置換到直線段上、增加軌道彈性和阻尼等措施來減緩波磨。張勝等人[12]、張喻涵等[13]基于摩擦自激振動理論,分別研究了輪對結構優化和直輻板車輪對波磨抑制的積極作用。然而,目前對波磨的研究僅局限于單S型輻板和直輻板車輪,針對雙S型輻板車輪卻鮮有研究。因此本文作者就雙S型輻板車輪的鋼軌波磨性能展開了討論,首先基于輪軌摩擦自激振動導致鋼軌波磨的理論,分別建立了正反雙S型輻板輪對[14-15]有限元模型;然后采用復特征值分析方法,研究當地鐵通過小半徑曲線時,雙S型輻板車輪對鋼軌波磨的影響;同時,與單S型輻板車輪進行對比分析。
1 理論和模型
1.1 復特征值分析方法
復特征值分析法被廣泛應用于制動噪聲的研究,是一種通過模態分析預測系統穩定性的方法。而CHEN等[5]在使用復特征值法研究鋼軌波磨問題時,發現YUAN[16]提出的方法可以有效地模擬輪軌之間的摩擦耦合,輪軌系統的動力學方程如下:
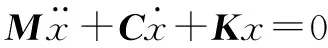
(1)
式中:M、C、K分別表示系統的質量矩陣、阻尼矩陣、剛度矩陣,為非對稱矩陣。
方程(1)的特征方程為
(Mλ2+Cλ+K)φ=0
(2)
式中:λ表示方程的特征值;φ表示特征向量。
求解得方程(2)的通解為
x(t)=∑φiexp[(αi+jβi)t]
(3)
式中:φi是第i階特征向量;αi+ jβi是其對應的第i階復數特征值。顯而易見,當特征值的實部αi>0時,位移將會隨著時間的增加而增加,即,系統的振動將會趨于不穩定。相應地,定義等效阻尼比ξ作為評判系統穩定性的參數,如下所示:
ξ=-2Re(λ)/|Im(λ)|
(4)
因此,當系統的等效阻尼比為負數時,系統可能發生不穩定振動,并且,等效阻尼比的絕對值越大,越容易發生不穩定振動。較為詳細的摩擦自激振動復特征值理論請參見文獻[5,17]。
1.2 雙S輻板車輪有限元模型
據王慶峰[18]統計,上海4號線使用的ZD840型車輪為雙S輻板車輪,這種類型的車輪輻板有較好的變形能力。文中針對雙S型輻板車輪,研究其對鋼軌波磨的影響。如圖1所示為3種不同輻板車輪的二維截面圖。其中,圖1(a)為傳統的雙S型輻板車輪,規定其S彎方向為正方向,由此可建立反雙S輻板車輪如圖1(b)所示。為驗證模型的正確性,以圖1(c)所示的傳統單S型輻板車輪進行對比分析。
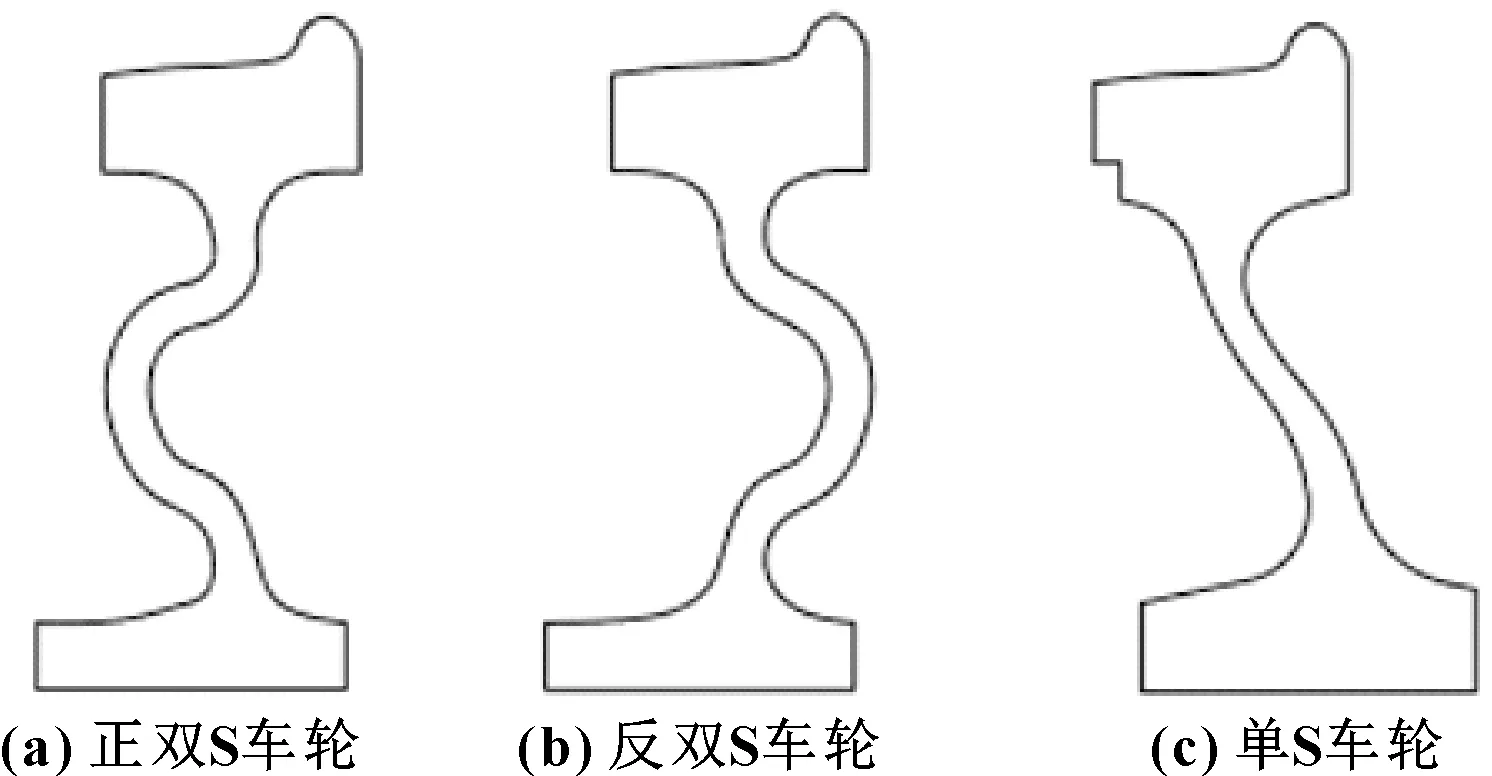
圖1 3種不同輻板車輪截面Fig 1 Section for three wheels with different web plates (a)positive double S plate wheel;(b)negative double S plate wheel;(c) single S plate wheel
根據圖1分別建立了正雙S型輻板車輪、反雙S車輪和單S型車輪的有限元模型,如圖2所示。單元類型均采用非協調單元C3D8I。
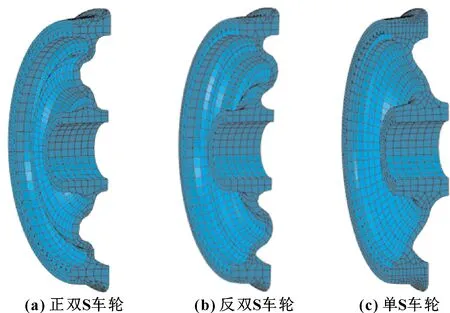
圖2 3種不同輻板車輪有限元模型Fig 2 FEM model for three wheels with different web plates (a)positive double S plate wheel;(b)negative double S plate wheel;(c) single S plate wheel
針對3種輻板車輪分別建立地鐵小半徑曲線輪軌系統有限元模型,包括一個輪對、兩條36 m長的鋼軌和系列短軌枕,如圖3所示。輪對和鋼軌的彈性模量為210 GPa,泊松比為0.3,密度為7 800 kg/m3。軌枕的彈性模量為190 GPa,泊松比為0.3,密度為2 800 kg/m3。
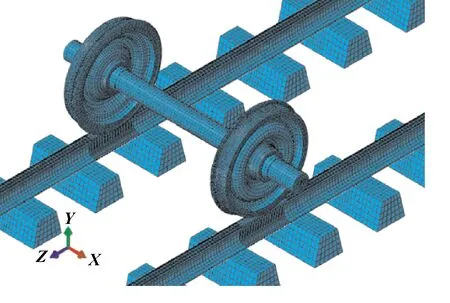
圖3 輪軌系統有限元模型Fig 3 FEM model of wheelset-track system
輪對和鋼軌之間采用面面接觸,鋼軌和軌枕之間、軌枕和地基之間均通過阻尼彈簧對連接,輪軌接觸模型如圖4所示[5]。文中研究工況是半徑R≤350 m的地鐵線路,通過在輪對兩端施加懸掛力(FSVL,FSLL,FSVR,FSLR)來實現,NL和NR,FL和FR分別是輪軌接觸點的法向力和蠕滑力。關于圖4中各參數介紹如表1所示。
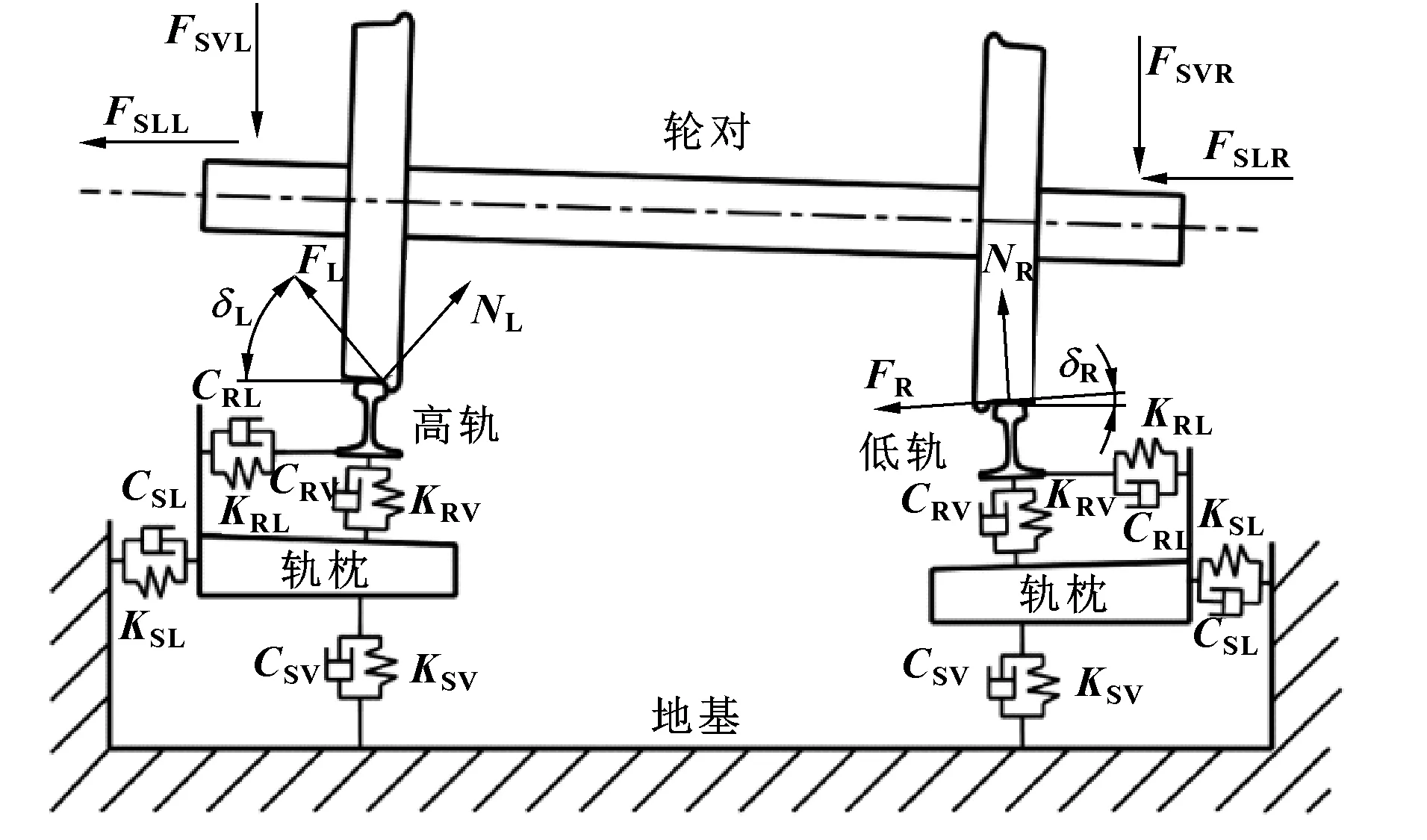
圖4 輪軌系統接觸模型Fig 4 Contact model of the wheelset-track system
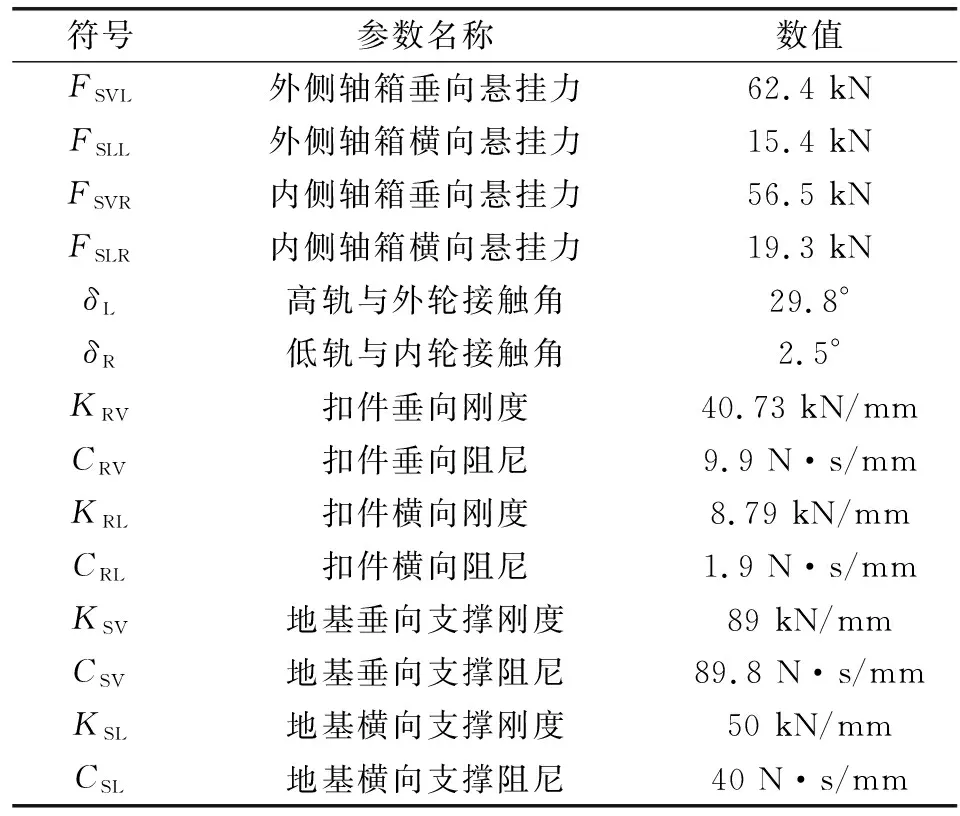
表1 模型參數介紹Table 1 The introduction of model parameters
2 計算結果及分析
2.1 3種輻板車輪對比分析
針對圖1所示3種輻板車輪,分別建立了輪軌系統有限元模型并進行計算,得到負等效阻尼比分布情況如圖5所示。
圖5(a)所示為正雙S輻板車輪模型的計算結果,發現沒有負等效阻尼比,即無波磨產生。為了校驗模型,對傳統的單S輻板車輪模型進行了計算,如圖5(c)所示,計算得到2個負等效阻尼比,主頻率為501.26 Hz,對應的等效阻尼比為-0.023 81,與文獻[5]中的結果一致,從而證實了無波磨模型的正確性。
反雙S輻板模型的計算結果如圖5(b)所示。可見有4個不穩定頻率產生,主頻率為431.4 Hz,對應的等效阻尼比為-0.028 3。所以相較于單S車輪和反雙S車輪,正雙S輻板車輪顯然消除了波磨。這可能是因為正雙S輻板比單S輻板彎曲較大,變形能力相對較好[18];而比反雙S輻板結構較優,對車輪的強度和剛度有積極的影響。
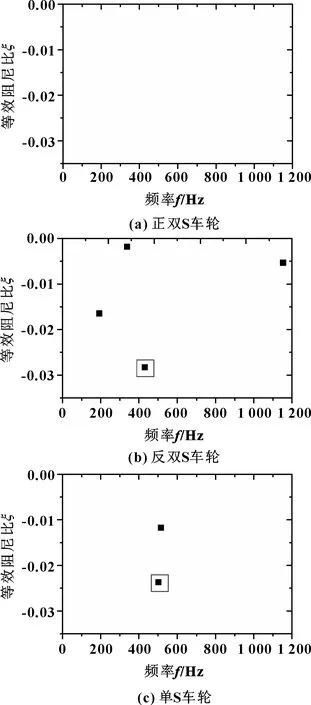
圖5 3種輻板車輪等效阻尼比分布Fig 5 Distribution of effective damping ratio for three wheels with different web plates (a)positive double S plate wheel;(b)negative double S plate wheel; (c) single S plate wheel
2.2 雙S輻板彎曲程度對鋼軌波磨的影響
如圖6所示為不同彎曲程度的正雙S輻板車輪截面圖,彎曲程度由大到小分別規定為大彎、中彎和小彎。建立相對應的三維有限元模型進行計算,結果顯示均無負等效阻尼比產生,說明正雙S輻板彎曲程度對鋼軌波磨沒有影響。
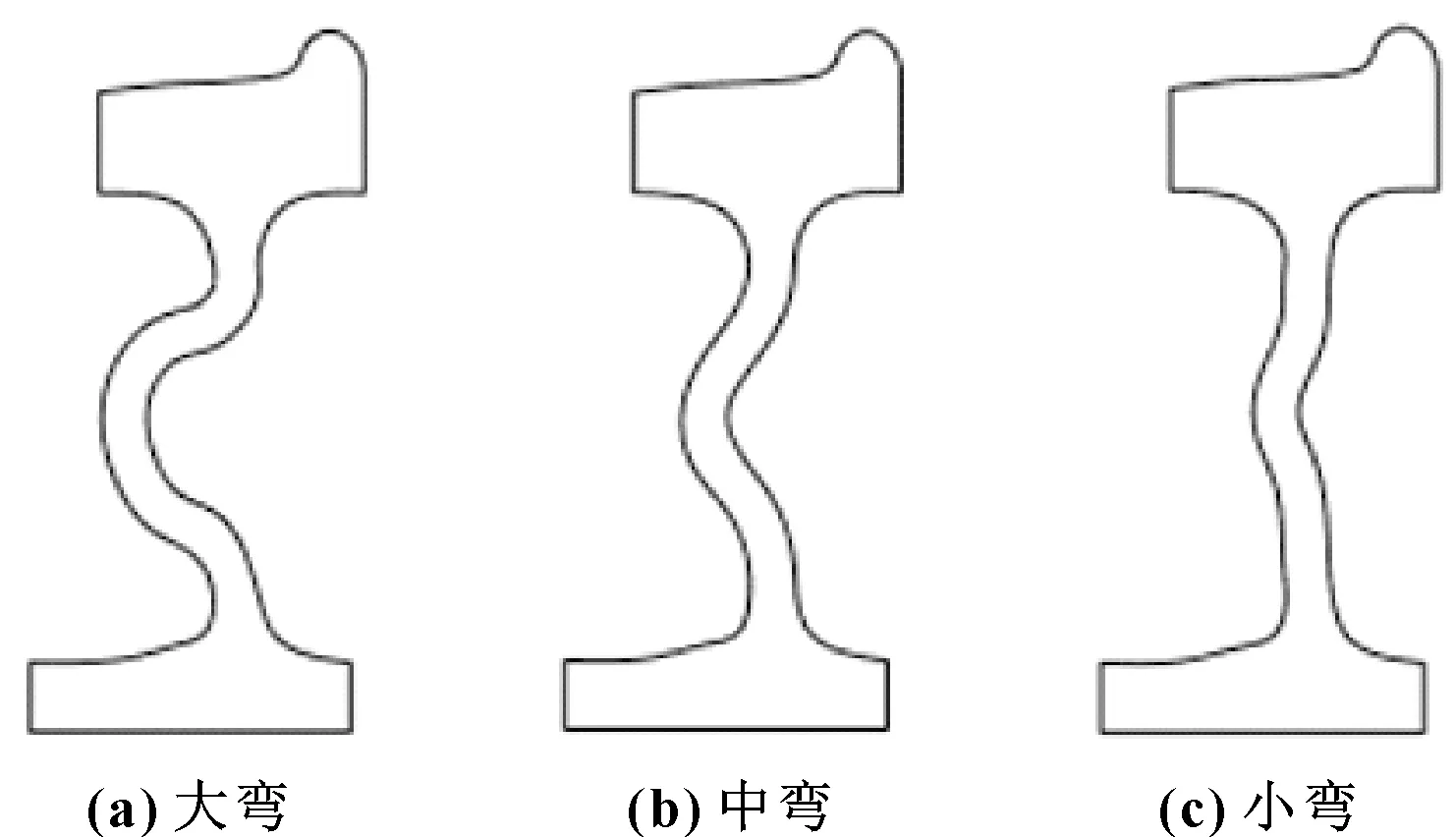
圖6 正雙S輻板不同彎曲程度截面Fig 6 Section of wheels with different double S-type web sizes (a)big bend;(b)middle bend;(c)small bend
同樣,根據圖7所示的反雙S不同彎曲程度分別建立輪軌系統模型,計算了等效阻尼比分布,結果如圖8所示。
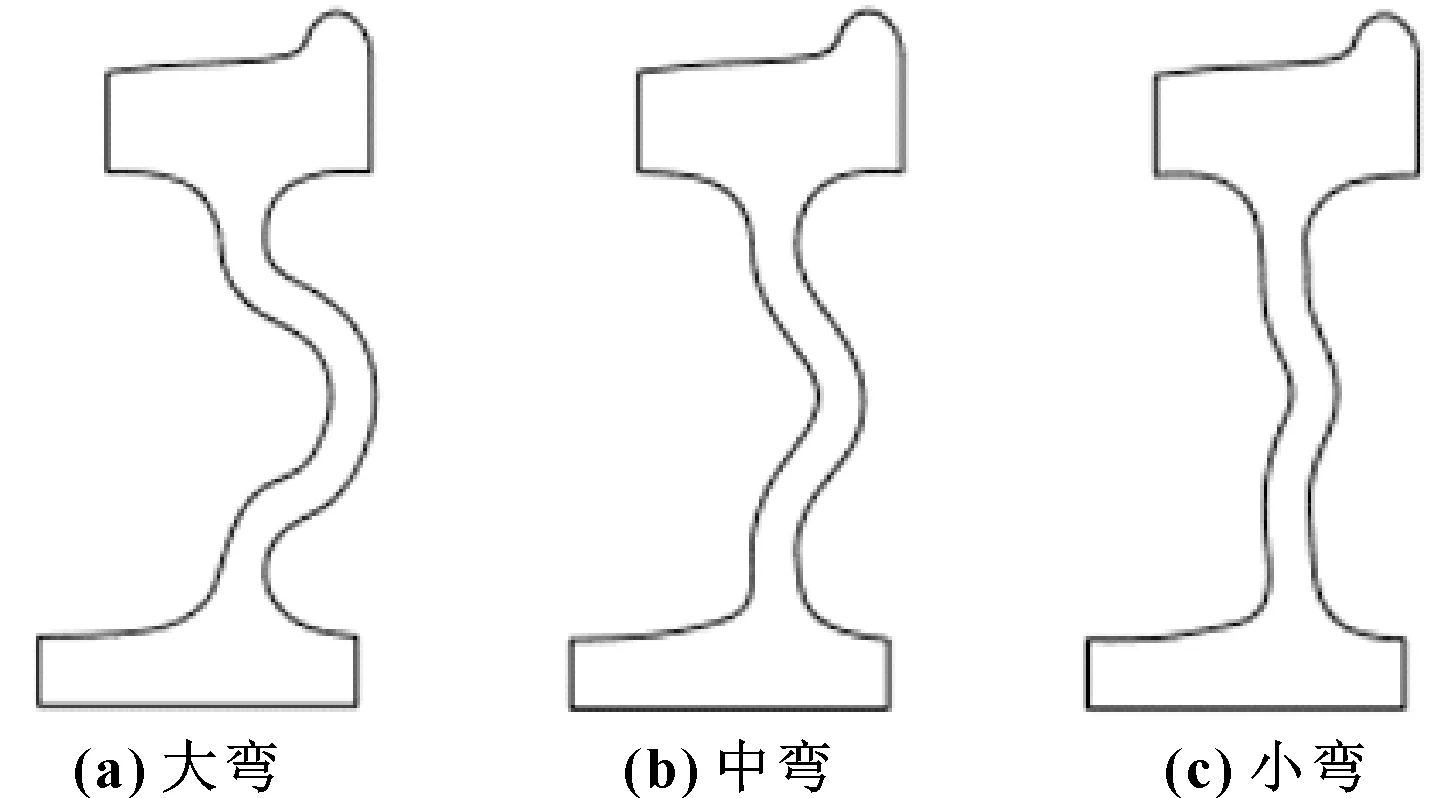
圖7 反雙S輻板不同彎曲程度截面Fig 7 Section of wheels with different negative double S-type web sizes (a)big bend;(b)middle bend;(c)small bend
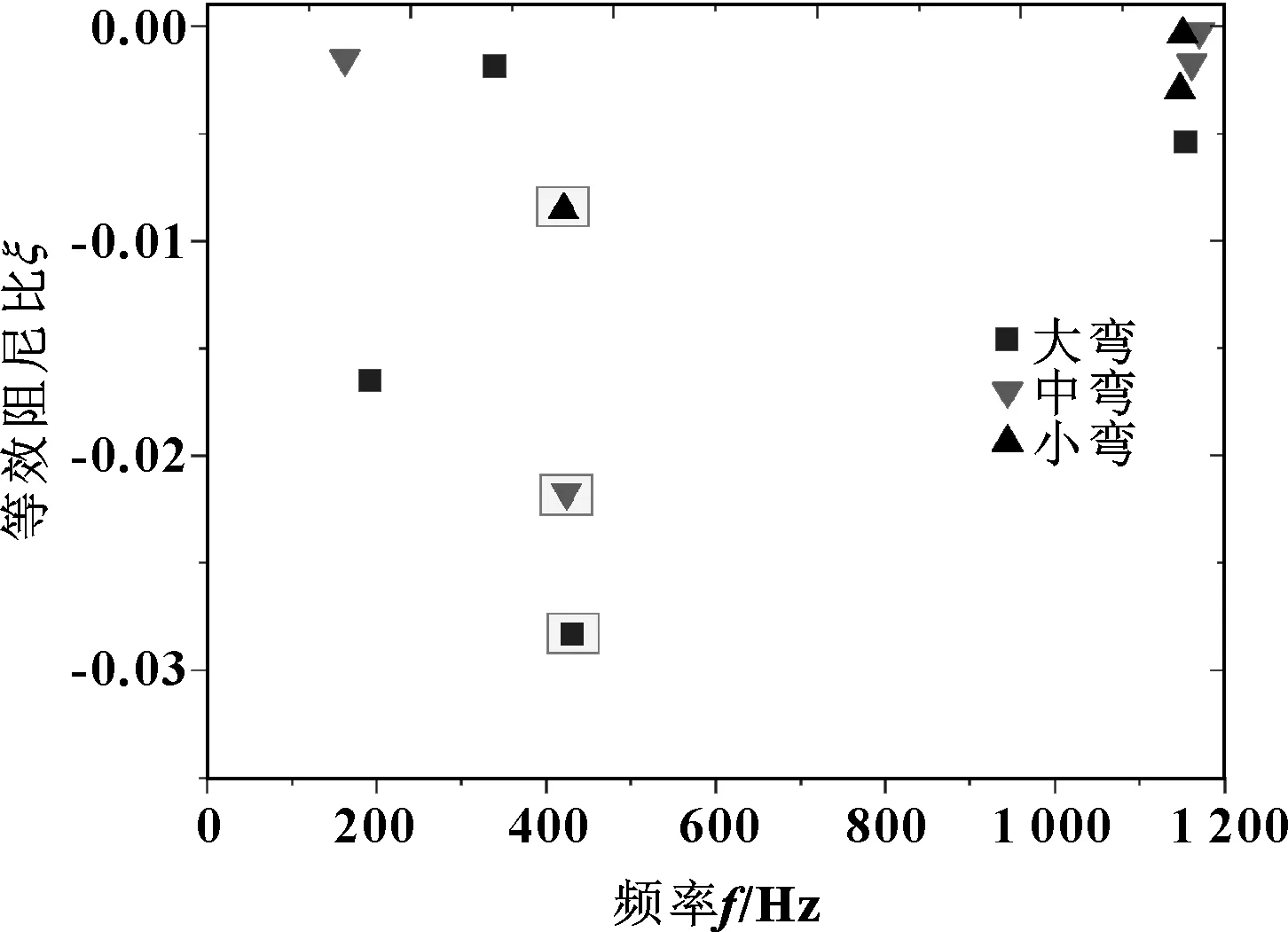
圖8 不同彎曲程度的反雙S輻板車輪等效阻尼比分布Fig 8 Distribution of effective damping ratio for the wheels with different negative double S-type web sizes
根據圖8,反雙S大彎模型產生4個不穩定振動頻率,其中主頻率為f=431.40 Hz,對應的等效阻尼比為ξ=-0.028 30。中彎模型也產生4個不穩定振動頻率,但是完全抑制了大彎模型產生的二階頻率339.73 Hz;主頻率為f=424.03 Hz,等效阻尼比為ξ=-0.021 71,相較于大彎模型均有所降低。小彎模型產生3個不穩定振動頻率,主頻率為f=420.21 Hz,等效阻尼比為ξ=-0.008 55,相較于中彎模型均有所降低,并且抑制了中彎模型產生的一階頻率162.85 Hz。總體來看,對于反雙S輻板模型,彎曲程度越大,輪軌系統越容易產生不穩定振動。這一結果與張喻涵等[13]的研究結果一致:直輻板有抑制波磨的能力,而小彎輻板趨近于直輻板,因此小彎模型更加穩定,大彎輻板車輪則可能是由于結構強度不夠導致了輪軌系統的不穩定。
不同彎曲程度反雙S輻板車輪對應的3個輪軌系統對應的主要振型如圖9所示。可見不穩定振動主要發生在低軌內輪,與實際相符。
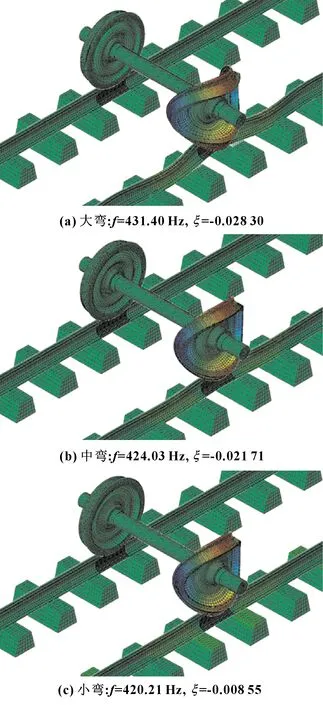
圖9 輪軌系統不穩定振動模態Fig 9 Mode shapes of unstable vibration for the wheelset-track system (a)big bend(f=431.40 Hz,ξ =-0.028 30); (b)middle bend(f=424.03 Hz,ξ =-0.021 71); (c)small bend(f=420.21 Hz,ξ =-0.008 55)
2.3 雙S輻板厚度對鋼軌波磨的影響
由以上兩小節分析討論可知,正雙S型輻板車輪是一種無波磨車輪,且輻板彎曲程度對結果無影響,而反雙S輻板車輪易產生波磨。所以,本節討論輻板厚度對波磨的影響,選取中等彎曲程度的正雙S型輻板車輪,輻板厚度t分別為33、23、13 mm,截面示意圖如圖10所示。
建立與圖10相對應的車輪的有限元模型,計算結果顯示33和23 mm厚度的輻板車輪均不發生不穩定振動,而13 mm厚度的車輪產生一個1 125.5 Hz的不穩定振動頻率,對應等效阻尼比為-0.000 10。說明正雙S輻板厚度對波磨影響不大,這可能是因為正雙S輻板結構本身的穩定性是由其正雙S彎決定的,與其輻板厚度關系較少,但也應綜合性能、強度、經濟等原則選取適當的輻板厚度。
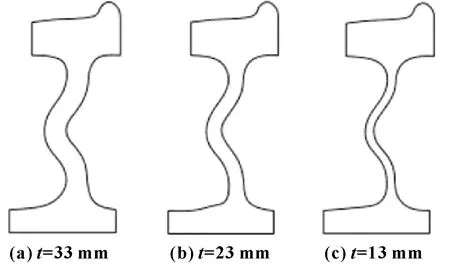
圖10 正雙S輻板不同厚度截面Fig 10 Section of the wheels with different thickness of the positive double S-type web (a)t=33 mm; (b)t=23 mm;(c)t=13 mm
3 結論
(1)正雙S型輻板車輪是一種無波磨車輪,其彎曲程度對結果無明顯影響,輻板厚度對波磨影響不大,但也應綜合考慮選取適當厚度的輻板車輪。
(2)反雙S型輻板容易引起鋼軌波磨,且輻板彎曲程度越大,越容易引起輪軌系統不穩定振動。
(3)反雙S型輻板模型預測的不穩定振動主要發生在低軌內輪,與實際相符,說明了摩擦自激振動理論的正確性。

