大學數(shù)學建模教學探索與實踐
杜 健,胡紅娟,夏 靜
(陸軍裝甲兵學院基礎部,北京 100072)
當今,科學技術以空前的廣度和深度飛速發(fā)展,許多現(xiàn)實問題必須通過模型的定量化描述、分析并求解,才可能得出科學的結論。因此,數(shù)學建模作為連接實際問題與數(shù)學問題的橋梁技術,承擔著越來越重要的作用。
1 大學數(shù)學建模教學現(xiàn)狀
大學開設數(shù)學建模課程,并在教學內(nèi)容、教學方法及課程考核等方面進行了一系列改革,極大地提升了學生的應用能力,在數(shù)學教學方面取得了一定的成效[1]。但是從當前的教學現(xiàn)狀來看,仍然存在許多問題,主要表現(xiàn)在盡管教師課上講了許多建模方法,學生面對實際問題時仍不知如何下手,無法建立有效的模型;建立的模型過于簡單,不能刻畫實際問題的本質(zhì)特征,得不出合理的問題結果;不能將數(shù)學建模的思想、方法,應用于專業(yè)課程的學習中,以解決專業(yè)問題;畢業(yè)論文設計中,想要運用數(shù)學建模技術解決某個專業(yè)課題,卻難以得出科學的結論。產(chǎn)生這些問題的主要原因是學生沒有真正掌握建模的思想與方法,仍處于模仿階段,僅將相關模型套用于問題中。
數(shù)學建模的本質(zhì)是對實際問題引入變量,做出適當?shù)暮喕图僭O,運用數(shù)學解析式刻畫變量間的基本關系或者結構,再通過數(shù)值求解,得出問題的解答,并應用于實際進行檢驗和推廣[2]。因此,課程教學不應僅局限于建模方法的傳授,更應著力于實際問題數(shù)學化,使學生在抽象的過程中,領略建模的思想與技術。在建模方法的講授過程中,教師應強化案例教學,使學生能夠分析問題中變量的基本關系,抽象出數(shù)學結構,建立數(shù)學模型。目前的教學更重視方法理論教學,而忽視實踐教學,導致學生較弱的建模能力無法適應社會對高素質(zhì)人才的需求。因此,對數(shù)學建模教學進行理論探討與實踐探索成為當前數(shù)學教育改革的重點。
2 大學數(shù)學建模教學的理論研究
2.1 將抽象思維形象化,使學生形成建模的基本意識
建立數(shù)學模型,難點是對實際問題進行抽象,這也是建模的本質(zhì)工作。大學數(shù)學課程具有的前沿性和高階性,無不滲透了抽象的過程[3]。相應地,數(shù)學建模教學要通過對相關學術文獻的分析,在解決問題的過程中引導學生學會分析變量之間所蘊含的基本關系,抽象出問題的量化解析式,學會對知識進行遷移,掌握抽象建模的基本方法。只有具備了抽象的基本方法,才能將抽象思維形象化,刻畫問題變量的關系才能變得更加簡潔明了,建立模型就會得心應手。因此,教學強化抽象思維過程,培養(yǎng)學生的應用意識,是當前建模教學應著力加強的環(huán)節(jié)。
2.2 將理論知識實用化,使學生掌握建模的基本方法
大學數(shù)學知識內(nèi)容龐雜,計算繁瑣,理論推證較為復雜。數(shù)學建模面對的則是實際問題,如何跨越理論與現(xiàn)實的鴻溝,是建模教學應著力解決的問題[4]。通過對現(xiàn)實問題基本關系的分析,用數(shù)學語言描述問題所蘊含的基本規(guī)律,使學生理解從實際問題到數(shù)學問題的抽象過程,掌握數(shù)學知識的實用化方法,了解知識的應用背景,從而建立理論知識與現(xiàn)實問題的通道,學會分析問題、解決問題的基本方法。在教學過程中,要充分還原知識的發(fā)現(xiàn)過程,培養(yǎng)歸納式思維,使知識學習及方法掌握變得快捷有效,提升建模本領。
2.3 充分引入案例教學,培養(yǎng)學生建模能力
數(shù)學建模教學比較注重一些常用方法的傳授,如微分方程建模、層次分析建模、時間序列建模等[5]。掌握建模的方法可以使學生較快掌握建模技術,面對實際問題時盡快融入某種方法,提出解決方案。但是,這樣也容易形成思維定式,不利于創(chuàng)造性思維的培養(yǎng)[6]。在教學過程中可引入案例教學,在解決問題的過程中根據(jù)實際需要,引出相應的數(shù)學概念、方法和理論,使知識的產(chǎn)生與發(fā)現(xiàn)變成自然而然的過程。這不僅符合知識的產(chǎn)生過程,而且與學生的思維認知過程一致,有利于學生掌握數(shù)學模型的基本方法,提升建模學習的興趣,增強應用意識,提升實踐能力,使學生具備初步的建模能力,解決現(xiàn)實生活中的實際問題。
2.4 加強數(shù)學實驗教學,提升學生建模創(chuàng)新水平
數(shù)學建模的對象是實際問題,因此模型求解更多的是數(shù)值求解,這就需要借助相應的數(shù)學軟件編寫程序,進行模擬求解。這實際是一個實驗過程,因此強化實驗教學必不可少[7]。為強化數(shù)學建模思想,可結合案例教學,加強數(shù)學實驗教學,向?qū)W生演示MATLAB、SPSS、SAS等統(tǒng)計軟件中的基本功能,展示數(shù)學模型的建立及求解過程[8]。通過數(shù)學工具軟件演示求解過程,學生在程序運行與調(diào)試過程中,學會運用數(shù)學思維思考和解決問題,體現(xiàn)應用數(shù)學知識進行數(shù)學建模的全過程,進而提高學生的建模創(chuàng)新水平。
3 大學數(shù)學建模教學實踐探索
3.1 抓住概念本質(zhì),強調(diào)知識的綜合應用
學會根據(jù)問題的要求構造必需的函數(shù),建立解決問題所需的數(shù)學模型。定積分概念是以求曲邊梯形面積為例引入的,通過分割、求和、取極限三個過程實現(xiàn)了曲邊梯形面積的計算,其中蘊涵了化整為零、積零為整的數(shù)學思想[9]。
教學中首先要歸納出兩點:
第一,用定積分解決問題的共性是求在[a,b]非均勻分布的一個整體量A。
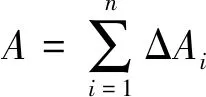

3.2 突出最基本的思想,領會解決問題的過程
微元法是定積分應用中的最基本方法,教學中要以定積分概念的引出過程為例,引導學生掌握微元法的基本概念,以及微元法所滿足的條件[10]。在實際問題中,如果問題變量在其取值區(qū)間上具有可加性,就可嘗試構造定積分的表達式去表示該變量,建立相應的數(shù)學模型解決問題。
從以下兩方面考慮建模:
第一,分析所解決的問題變量U,滿足以下條件:A.U與變量x的變化區(qū)間[a,b]有關。B.U對于區(qū)間[a,b]具有可加性。C.U部分量ΔUi可近似地表示成f(ξi)·Δxi。
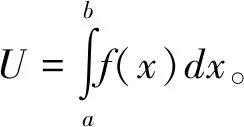
3.3 掌握最基本的方法,培養(yǎng)創(chuàng)新思維能力
優(yōu)化問題是數(shù)學建模的重要方面,根據(jù)定積分的幾何意義,確定幾何圖形面積、體積的最值。
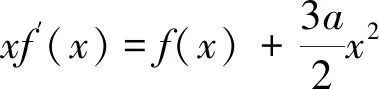
為2,求函數(shù)y=f(x),問a為何值時,圖形S繞x軸旋轉(zhuǎn)一周所得的旋轉(zhuǎn)體體積最小?
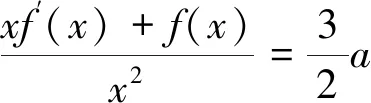
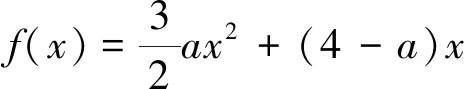

所以當a=-5時,該旋轉(zhuǎn)體體積為最小。
4 結語
大學數(shù)學建模教學關鍵在于使學生了解數(shù)學建模的基本思想,掌握從實際問題中提煉數(shù)學關系的方法,檢驗學生的知識結構和綜合運用能力。面對信息社會的深刻變革,學生只有掌握了數(shù)學建模的思想與方法,才能在面對實際問題時,運用數(shù)學的思維意識,建立問題的模型結構,創(chuàng)造性地解決問題,凸顯數(shù)學教育的功能價值,這也正是大學數(shù)學教學的意義所在。

