幾何畫板視角下一道中考數學試題的變式探究*

內江師范學院數學與信息科學學院 (641100) 張森祥 余小芬

幾何畫板作為一個適用于幾何教學和學習的工作軟件平臺，可通過繪圖、度量、變換等基本功能完成對中學數學圖形的繪制、動態問題的探究，不僅能有效輔助教師課堂教學，也幫助學生更直觀、深刻地理解圖形或問題.同時，利用幾何畫板實驗探究功能對數學問題展開變式拓展，可衍生出系列關聯問題，以此為學生提供探究性的學習環境，培養學生對數學的理解能力和創新意識.本文以2019年四川省南充市中考數學第25題為例，運用幾何畫板展開變式探究.

一、原題呈現

試題(2019年南充市中考數學25題)如圖1，拋物線y=ax2+bx+c與x軸交于點A(-1,0)，點B(-3,0)，且OB=OC．

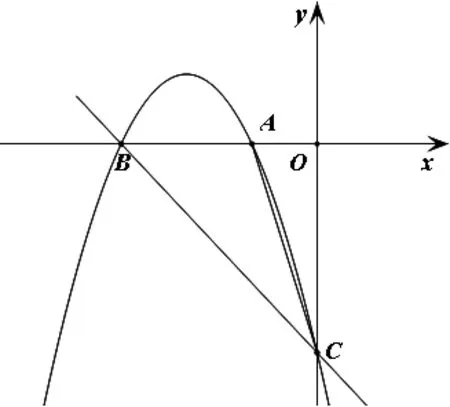
圖1

(1)求拋物線的解析式；

(2)點P在拋物線上，且∠POB=∠ACB，求點P的坐標；

(3)拋物線上兩點M、N，點M的橫坐標為m，點N的橫坐標為m+4．點D是拋物線上M、N之間的動點，過點D作y軸的平行線交MN于點E.①求DE的最大值；②點D關于點E的對稱點為F，當m為何值時，四邊形MDNF為矩形．

二、對問題(2)的變式

問題(2)是拋物線動點問題.解決的關鍵是構造相似三角形，利用對邊成比例求解動點坐標.考查勾股定理、三角形面積、銳角三角函數等知識，涉及等面積法、坐標法等基本方法，滲透化歸轉化、分類討論等數學思想.

變式1 點P在拋物線上，且∠PAB=2∠ACB，求點P坐標.

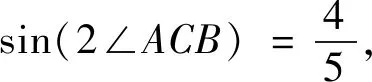
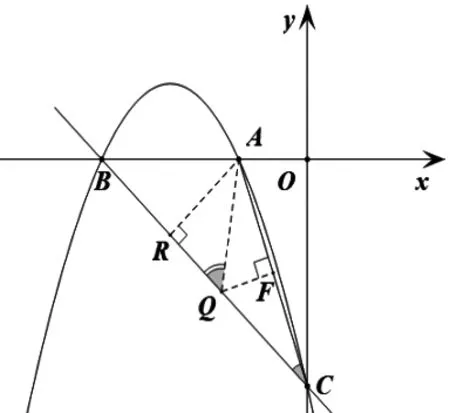
圖2

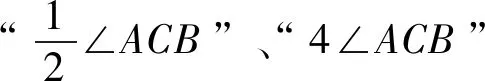
三、對問題(3)①的變式

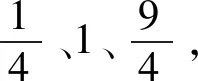
變式2 將條件(3)中點N橫坐標改變為m+3，其余條件不變，求DE的最大值.由此你能猜想出當N點橫坐標變為m+a(a≠0)時，DE的最大值嗎？

根據以上幾何畫板的探究，不難得到當DE為最大值時，不論點M在拋物線上如何變化，ΔMDN的面積為一定值，故而考慮利用面積定值求解線段長度的動態問題，得到變式3.

變式3 在(3)條件基礎上，過點E作EG垂直于DM于點G，試求點M運動過程中EG長度的最大值.

當然，除了求線段EG的最大值，同理可設置問題求點N到線段MD的最大值.同時，利用幾何畫板作出DM、DN兩邊的高，拖動點M可發現所作兩高與DE存在相交于一點的情形，并且此時FG與MN相互平行，故又可利用等腰三角形性質、三角形高交于一點等知識得到如下變式4.

變式4 在(3)條件基礎上，過點N作NF垂直于MD于點F，過點M做MG垂直于DN于點G，當NF、MG與DE相交于一點，試判斷FG與MN的位置關系并求FG.

四、對問題(3)②的變式

問題(3)②以矩形的性質為知識載體，考查動點問題的求解.事實上，平面上四點要構成矩形也即是四點共圓.于是考慮引入圓，利用圓中相關知識產生變式.

在(3)②條件基礎上，通過利用幾何畫板構造出以點E為圓心，MN為直徑的圓(如圖3)，可以發現，圖中存在多對相等角及三角形相似情形.由此，利用圓周角定理等知識，可得到如下變式.

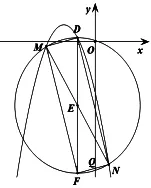
圖3

變式5 如圖4，在(3)條件基礎上，以點E為圓心，MN為直徑作圓，圓E與y軸交于點Q，當m為何值時，∠DMN=∠DQN.

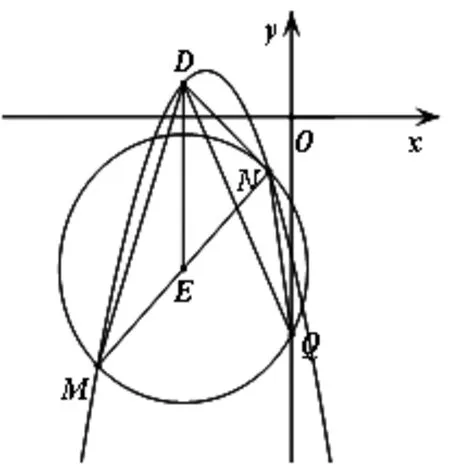
圖4

在變式5中，若記DQ與MN交于點S，易觀察得到ΔMDS與ΔNQS相似，進而得到如下變式6.

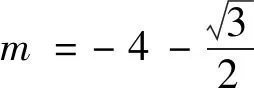
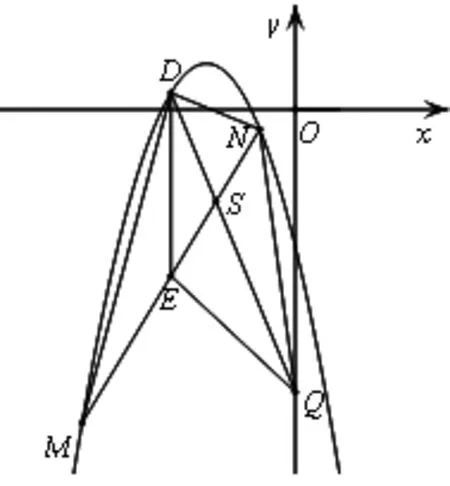
圖5

上述探究中，若改變圓心位置，又能產生哪些新的變式呢？為此，以點M為圓心，ME為半徑構造圓，并過點D作該圓的切線DS，通過拖動點M位置發現，點M運動過程中存在如圖6所示的特殊位置，則可根據切線長定理，得到如下變式7.

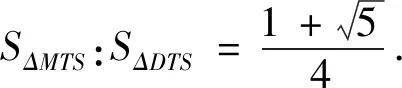
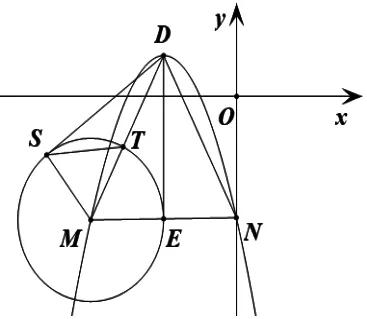
圖6

本文利用幾何畫板對原試題展開了圖形重構、問題探究，得到了幾個問題變式，幫助學生形成數學觀察、猜想的意識，增強問題分析、解決的能力，提升直觀想象和數學運算的學科素養.