基于課程思政的數學分析課程教學設計探討
陳立宇,王偉芳
基于課程思政的數學分析課程教學設計探討
陳立宇,王偉芳
(唐山師范學院 數學與計算科學學院,河北 唐山 063000)
“立德樹人”是教育的根本任務,如何在教育的過程中處理好知識傳授和價值引領的關系,做好“課程思政”,真正提高人才培養的質量,是值得每一位教師思考的問題。本文以數學分析課程為例,探討如何在數學分析課程的教學中融入思政元素。
課程思政;價值引領;數學思維;創新意識
高校教師不僅承擔著傳授專業知識的重任,更要培養學生正確的三觀,塑造學生健全的人格。“培養什么人,為誰培養人,如何培養人”是每位高校教師首先要回答的問題。育人工作不只是通過學生工作和思政課程來實現,更應充分挖掘專業課程的思政功能,將思政元素與專業課有機融合在一起,通過專業課程教學實現對學生潛移默化的積極影響。數學分析是數學與應用數學、信息與計算科學等專業的基礎課程,是一門理論體系完備、內容豐富、應用十分廣泛的課程,該課程的教學質量和學習效果直接影響到學生對專業的學習興趣和未來的職業規劃,通過該門課程的學習,學生可進一步掌握數學知識、培養數學思維、提升數學素養。由于數學類專業學習難度大、要求高,需要學生具備克服困難的精神、嚴謹的學習態度和科學的數學思維,這些素養則需要通過專業基礎課程的教學來培養。
本著“能融則融、宜融則融”的原則,精心設計教學,重視知識目標和能力目標,更要融入情感態度與價值觀的教學目標,在授課過程中,潛移默化地開展思想引領,更好地服務于學生的成長、成才。
1 發揮價值引領作用,培養民族自信和科學的精神
1.1 家國情懷的培養
在引入反常積分時,引例第二宇宙速度問題歸結為無窮積分問題,說明國家的航天事業需要我們這樣具有專業知識的人才,激勵學生們努力學好專業知識,練就為國家做貢獻的過硬本領。通過簡要介紹從毛主席提出要搞人造衛星到我國成為第五個獨立發射人造衛星的國家這一段歷史,培養學生的家國情懷。
1.2 民族自信的培養
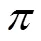
2 提升認識高度,培養學生的哲學思維
2.1 一般與特殊的關系

都存在且相等。
海涅定理是德國數學家海涅(Heine)給出的,它建立了數列極限和函數極限的橋梁,而數列極限是特殊的函數極限,利用海涅定理可以將數列極限轉化為函數極限,即可以通過一般的函數的極限來求特殊的數列的極限。
2.2 整體與部分的關系
數列與子列極限的關系充分體現了整體與部分的關系。

數列及其子列的上述關系深刻揭示了變量變化的整體與部分之間的關系[3]。
2.3 普遍聯系的觀點
不定積分和定積分是分別定義的,微積分學基本定理將這兩個看似不相干的概念聯系了起來,并揭示了它們之間的內在聯系。
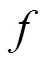
類似的,反常積分和無窮級數是兩個不同的概念,而積分判別法也將兩者聯系起來。數學分析中類似的體現普遍聯系觀點的結論還有很多。
2.4 量變與質變的觀點
在極限定義的形成過程中,經歷了三個階段:
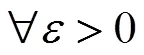
每一次質的飛躍都是量變的積累,是量變達到一定程度的必然結果。任何事物的發展都是量變與質變的辯證統一,數學分析的發展也不例外。
3 優化教學過程,培養學生的數學思想
3.1 化歸轉化思想
不定積分作為非構造性定義,其定義并未給出不定積分的求法,因此求不定積分問題最終都歸結為將被積函數變形為基本積分表中不定積分的類型,如何轉化,就需要學生掌握化歸轉化思想,如
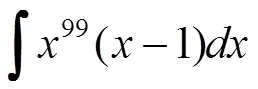
兩個不定積分,被積函數均為單項式與多項式的乘積,但前者直接乘開即可,后者則因為多項式項數過多而不好表示。
在教學過程中,通過精心設計例題,對例題歸類,啟發學生思考,在掌握了
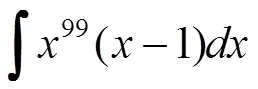
的求法后,分析用同樣的方法求
3.2 數形結合思想
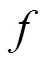
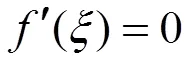
如圖1所示,羅爾中值定理的幾何意義是滿足定理條件的曲線上必有一點處的切線平行于軸,接下來啟發學生思考,如果將曲線的右端點上移至如圖2位置,那么可以得到什么結論?
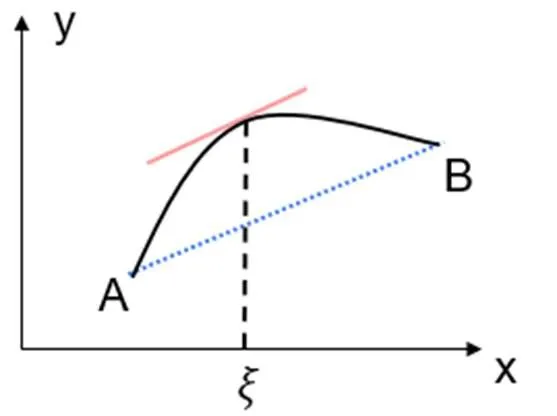
圖2 拉格朗日中值定理的幾何意義
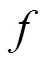
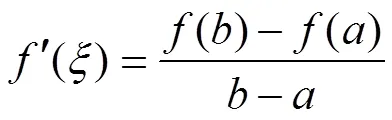
在給出拉格朗日中值定理后,進一步引導學生思考:如果曲線由參數方程給出,拉格朗日中值定理的結論又是怎樣的呢?這樣就引出了柯西中值定理。
3.3 反例思想
多元函數可微的必要條件指出:可微必連續,可微必可偏導,但反之不一定成立,反例怎么舉?
根據可微的必要條件,不可偏導一定不可微,因此,在找連續不可微的反例時,就可以找連續且偏導數不存在的函數,而函數
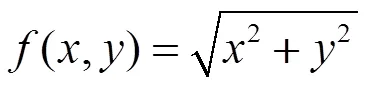
在教學過程中,通過啟發式教學法,引導學生找出反例,從而更好地理解和掌握結論。
3.4 類比思想
數學分析中四次出現阿貝爾和狄利克雷判別法,定理的條件都有相似之處。在教學過程中,提醒學生進行類比歸納,啟發學生自主構建知識的網絡。
4 創新教學方法,培養學生的團隊協作意識和創新精神
4.1 學以致用的意識
在講授條件極值時,可以先提出一個問題:易拉罐為什么要這么設計?然后分析如果將易拉罐分別設計成長方體和圓柱體,怎么設計用料最省?通過探索讓學生明白易拉罐這樣設計的原因,理解如何通過數學建模為企業節約成本,增強學生的節約意識和環保意識[7]。
4.2 團隊協作意識
在講授一元函數最值時,已知閉區間上連續函數的最值的求法,若把閉區間換作開區間,最值該如何去求?采用小組討論法,課前發布討論任務,分小組討論,課上各小組充分發言,最后教師點評、總結、補充、提煉。通過參與式、互動式教學,充分調動學生的學習積極性,培養學生的團結協作意識。
4.3 創新意識
在講授反常積分的阿貝爾狄利克雷判別法時,采用啟發式教學,由柯西收斂準則和積分第二中值定理推導出兩個定理的條件[5],在還原定理的發現過程,培養學生的創新意識和思維能力。
[1] 孫玉芹,劉建軍.有限的生命與無限的價值——“數列的極限”教學案例[J].教育教學論壇.2019(42):175.
[2] 華東師范大學數學系.數學分析(第4版上冊)[M].北京:高等教育出版社,2010:54.
[3] 李文林.數學史概論(第3版)[M].北京:高等教育出版社, 2011:79-84.
[4] 華東師范大學數學系.數學分析(第4版下冊)[M].北京:高等教育出版社,2010:118-125.
[5] 反常積分的阿貝爾和狄利克雷判別法教學初探[J].唐山師范學院學報.2016(2):27-29.
[6] 朱國衛.以海涅定理為例談數學分析中的證明,直覺和感悟[J].吉林省教育學院學報,2010,26(7):154.
[7] 數學分析“課程思政”的實踐與思考[J].創新教育研究, 2019,7(5):675-678.
The Teaching Design of Mathematics Analysis Course Based on Ideological and Political Education Through Curricula
CHEN Li-yu, WANG Wei-fang
(School of Mathematics and Computational Sciences, Tangshan Normal University, Tangshan 063000, China)
“Moral education” is the fundamental task of education. How to deal with the relationship between knowledge imparting and value leading in the process of education, achieve “ideological and political education through curricula”, and really improve the quality of talent training are worth thinking. Taking the course of mathematical analysis as an example, how to integrate ideological and political elements into the teaching of mathematical analysis is analyzed.
ideological and political education through curricula; value leading; mathematical thinking; innovation consciousness
O171
A
1009-9115(2021)06-0112-04
10.3969/j.issn.1009-9115.2021.06.026
2020-12-08
2021-07-06
陳立宇(1990-),男,河北唐山人,博士,講師,研究方向為流體仿真模擬。
王偉芳(1984-),女,河北定州人,碩士,講師,研究方向為基礎數學。
(責任編輯、校對:趙光峰)

