深溝球軸承-轉軸系統回轉運動建模與分析

馮曉飛，王德倫

（大連理工大學機械工程學院，遼寧大連 116024）

0 引言

軸承作為機械加工系統的核心部件，其精度特性直接關系到整機的性能。Jones[1]建立了可以求解不同滾動體個數的軸承內圈滾道相對于外圈滾道位移的擬動力學模型；Harris[2]考慮了軸承潤滑條件和摩擦等因素的影響，分析了軸承在徑向、軸向和力矩聯合作用下軸承內外圈的運動關系；Noguchi等[3]從理論上研究了軸承滾道波紋度與滾動體直徑不同誤差形式與大小對軸承內圈跳動的影響；Okamoto[4]將數值模擬與試驗檢測相結合，分析了軸承軸心運動軌跡與零件形狀誤差的關系；留劍等[5]分析了軸承內外圈滾道及滾動體上的波紋度對軸承跳動的影響規律；王德倫等[6]采用剛性輪廓曲面等效零件的幾何誤差，提出彈性冗余空間機構模型。

1 軸承模型建立

軸承主要由內圈、外圈、滾動體和保持架4個基本元件組成。為了簡化計算，模型做出如下假設：1）在載荷作用下，軸承的內外圈不發生整體變形，只會產生相對的位移；2）軸承的滾動體與滾道為局部接觸，變形規律符合赫茲接觸理論；3）不考慮軸承保持架的影響，保持架只發揮固定滾動體處于理想位置的作用；4）不考慮彈流潤滑條件的變化。

1.1 滾動體與滾道幾何關系

基于軸承各組件的幾何關系，建立坐標系：以外圈滾道幾何中心為原點的固定坐標系{Of; if, jf, kf}，以內圈滾道幾何中心為原點的移動坐標系{Om;im, jm, km}，滾動體與內外滾道的幾何關系如圖1所示。

圖1 滾動體與滾道位姿關系

建立滾動體與滾道幾何位移方程：

式中：j為滾動體編號；Rij、Roj分別為滾動體j與軸承內、外圈滾道接觸處曲面的矢量方程；Nij、Noj分別為滾動體j與軸承內、外圈滾道接觸處法線方向矢量；rgj為滾動體j的半徑尺寸；Rgj為滾動體j的質心位置；δij、δoj分別為滾動體j與內、外滾道法向接觸變形量；Rm表示軸承內圈幾何中心位置。

1.2 滾動體與內外圈接觸力

根據赫茲接觸理論，滾動體與內外滾道之間的接觸載荷為：

式中：Fij、Foj為法向接觸載荷，是標量；Lij、Loj分別為內、外滾道與滾動體接觸摩擦方向。

1.3 滾動體離心力

設軸承內圈的旋轉角速度為ωi，滾動體的公轉角速度與保持架的角速度相同，均為ωb，滾動體的公轉角速度ωb與內圈回轉的角速度ωi的關系為

式中：Dm為軸承節圓直徑；Di為軸承內圈直徑；Dwj為滾動體j的實際直徑尺寸。

1.4 軸承力學平衡方程

1）滾動體力平衡分析。

在運動過程中，軸承滾動體受到來自軸承內圈、外圈的作用力及高速回轉運動時的離心力，對于滾動體j的受力如圖2所示。

圖2 滾動體受力示意圖

根據圖中滾動體受力情況，建立滾動體j的力平衡方程：

式中：Fij、Foj分別為內圈與滾動體j的接觸載荷；Tij、Toj分別為內圈與滾動體j之間的摩擦力；Fcj為滾動體j的離心力；Ggj為滾動體j的重力。

2）內圈力平衡分析。

內滾道受力如圖3所示。

圖3 內圈受力示意圖

在全局坐標系下，先計算得出每個滾動體的受力狀態，再代入軸承內圈平衡方程進行計算，求解出軸承內圈質心的位姿變化。平衡方程如下：

式中：Gi為軸承內圈的重力；Mi為施加的力矩；F為施加在內圈上的外載荷。

2 軸系模型建立

在柔性軸系統中，軸在受到徑向載荷后，轉軸會發生一定的彈性彎曲變形，并產生力矩載荷。軸系結構如圖4所示。

圖4 軸系結構受力簡圖

根據軸系受力簡圖，建立軸系平衡方程：

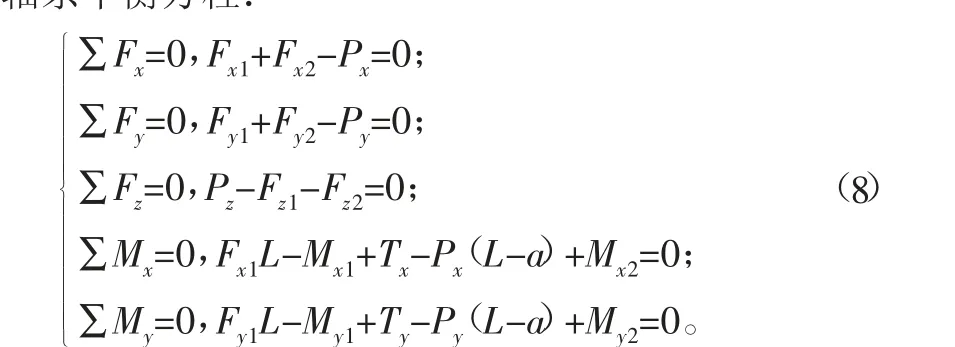
通過求解上式，可得到軸承上載荷與轉角及位移之間的關系。當深溝球軸承內圈所受外載荷為F={Fx，Fy，Fz，Mx，My}，位移為δ={ux，uy，uz，θx，θy}，根據軸承載荷與位移之間的關系，利用差分法就可計算得出軸承剛度矩陣為

采用歐拉-伯努利梁單元對軸的彎曲變形進行等效，軸的整體剛度矩陣是由每個梁單元的剛度矩陣組集而成。當軸被劃分為M個節點，每個節點存在6個自由度，則轉軸的剛度矩陣為6M階矩陣。將2個軸承剛度矩陣疊加到轉軸剛度矩陣對應的節點上，組成裝配后軸系整體的剛度矩陣。對于雙支點支承軸系結構，令外載荷矩陣為

由式KU=P可知，若K和P已知，便可計算得出軸上各個節點的位姿狀態，從而計算出轉軸在運轉過程中的位姿變化。

軸系回轉運動模型的計算流程圖如圖5所示。

圖5 軸系模型計算流程圖

3 算例分析

軸系結構如圖4所示，具體結構參數如表1所示。

表1 軸系結構參數

3.1 軸向載荷對回轉精度的影響

在軸上施加固定的徑向載荷，通過改變軸向載荷的大小，分析軸向載荷對軸系回轉精度的影響規律。令徑向載荷為3000 N，軸向載荷從500 N到1500 N變化，變化步長為50 N，計算出在不同的軸向載荷作用下軸系載荷位置處軸向與徑向的位移誤差，繪制關系曲線如圖6所示。

圖6 軸向載荷對軸系回轉誤差的影響

結果表明，隨著軸向載荷的增大，軸系的軸向誤差急劇減小，并且當軸向載荷大于1100 N時，軸向位移誤差趨近于某一較小值。軸系通過安裝時施加一定的軸向力可以提高軸系的回轉精度，對于本模型，當軸向預緊力大于1100 N時，有利于系統的精度達到最佳。同時，軸上施加的軸向載荷對于軸系回轉運動的徑向誤差影響較小。

3.2 徑向載荷對回轉精度的影響

在軸上施加固定的軸向載荷，通過改變徑向載荷的大小，分析徑向載荷對軸系回轉精度的影響規律。令軸向載荷為1000 N，徑向載荷從1000 N到8000 N變化，變化步長為500 N，計算出在不同的徑向載荷作用下軸系載荷位置處軸向與徑向的位移誤差，繪制關系曲線如圖7所示。

圖7 徑向載荷對軸系回轉誤差的影響

結果表明，徑向載荷對于軸系回轉運動的軸向誤差影響較大，隨著軸上徑向載荷的增大，軸系的軸向誤差逐漸變大，而徑向載荷變化對軸系的徑向誤差影響較小，且當徑向載荷超過7000 N時，軸系的徑向位移誤差值增加逐漸緩慢。

3.3 載荷位置對回轉精度的影響

軸上載荷作用位置不同，軸承所受的載荷不同，所以轉軸在載荷作用位置處的各方向移動量也不同。如圖4所示，軸承1與載荷施加位置的距離為a，令a的取值范圍為20～280 mm，變化步長為20 mm，施加載荷Fy=2000 N，Fz=1000 N。計算出當載荷位置不同時，軸系載荷處軸向與徑向的位移誤差，繪制關系曲線如圖8所示。

圖8 載荷位置對軸系回轉誤差的影響

結果表明，載荷位置的變化對軸系回轉運動的軸向誤差影響較大，而對徑向誤差影響很小。對于軸承對稱布置的雙軸承支承軸系結構，當施加載荷位置位于兩軸承中間位置時，軸系的徑向、軸向誤差達到最小值，此時軸承-轉軸系統的回轉精度為最佳。

4 結論

從深溝球軸承組件的幾何關系、載荷約束關系出發，建立軸承-轉軸系統回轉運動精度模型。通過改變軸上載荷大小與載荷施加位置，分析載荷對軸承-轉軸系統回轉運動的影響規律，得出結論如下：1）隨著軸向載荷的增大，軸系回轉運動的軸向位移誤差減小，而對徑向位移誤差影響較小；2）隨著徑向載荷的增大，軸系回轉運動的軸向位移誤差增大，而對徑向位移誤差影響較小；3）對于軸承對稱布置的雙支點支承軸系，當載荷位置在兩軸承中間位置時，回轉軸系的徑向、軸向誤差達到最小值，此時系統的回轉精度達到最佳狀態。