基于RISC-V向量指令的稀疏矩陣向量乘法實現(xiàn)與優(yōu)化*
顧 越,趙銀亮
(西安交通大學(xué)計算機(jī)學(xué)院,陜西 西安 710049)
1 引言
隨著云計算與物聯(lián)網(wǎng)浪潮的興起,人們對可定制、低功耗和高性價比CPU的需求日漸增加。最初由加州大學(xué)伯克利分校研究人員開發(fā)的開源指令集架構(gòu)RISC-V,憑借其可伸縮、可擴(kuò)展和模塊化的特性[1 - 3],在相關(guān)領(lǐng)域的影響力逐漸擴(kuò)大。該指令集由整數(shù)基本指令和多個拓展指令集組成[4],拓展指令集中包括了用于向量處理的V指令集——RV32V。RV32V目前仍在GitHub上開發(fā)[5],最新穩(wěn)定版本為v0.9。與傳統(tǒng)SIMD向量架構(gòu)不同的地方在于,RISC-V向量指令集具有向量寄存器可配置的特性,解決了向量計算中向量長度不可知的問題[6,7]。
向量計算中的稀疏矩陣與向量乘法SpMV(Sparse Matrix-Vector multiplication),常用于科學(xué)計算和工程應(yīng)用問題中的大規(guī)模稀疏線性系統(tǒng)求解[8],其實現(xiàn)與優(yōu)化一直是高性能計算領(lǐng)域的研究重點(diǎn)。因稀疏矩陣具有非零元素占比少的特性,研究人員常采用壓縮存儲格式來提高存儲效率,又因非零元素分布和硬件設(shè)備的多樣性,其存儲格式也具有多樣性[9]。如COO(COOrdinate list format)[10]格式以行坐標(biāo)、列坐標(biāo)和值組成的三元組對稀疏矩陣中非零元素進(jìn)行存儲,簡單直觀靈活,但不利于計算和向量化。另一種常用的存儲格式CSR(Compress Sparse Row format)格式,將所有非零元素的值和列索引按行順序存儲在2個單獨(dú)的數(shù)組中,第3個數(shù)組保留指向這些數(shù)組中每一行的起始位置的指針。它的主要優(yōu)點(diǎn)是對任何類型的矩陣元素分布都有很好的壓縮比,其主要缺點(diǎn)為數(shù)據(jù)局部性差,存在寫沖突、負(fù)載不均衡等問題[11]。ELLPACK(format used by ELLPACK system)格式可在GPU和矢量體系結(jié)構(gòu)中高效運(yùn)算,但需要付出額外的存儲代價[12]。它以m*k的矩陣存儲數(shù)據(jù),其中k的大小取決于每行非零元素個數(shù)中的最大值。面對不規(guī)則矩陣時,其存儲和計算效率都會退化。HYB(HYBrid format)格式[13]結(jié)合了ELLPACK格式和COO格式,對每行中超過閾值的非零元素使用COO格式存儲,以減少ELLPACK格式中零元素的填充,兼顧計算效率的同時節(jié)約了存儲空間。
SELLPACK(Sliced ELLPACK format)[14]格式是基于ELLPACK格式的改進(jìn)。通過將矩陣行向量按照其非零元素數(shù)量排序,以固定行數(shù)對矩陣分片,對得到的矩陣塊分別使用ELLPACK格式存儲,提高了存儲不規(guī)則矩陣的效率和吞吐量。更進(jìn)一步地,SELL-C-σ(Sliced ELLPACK format with parameterC,σ)格式[15]通過限制排序窗口避免了重新排列整個矩陣的高昂代價,同時充分利用了矩陣相鄰行與被乘向量x相乘時,對向量x訪問的局部性。針對Intel 公司設(shè)計的異構(gòu)眾核處理器Xeon Phi,Liu等人[16]提出了ESB(ELLPACK Sparse Block)格式,該格式引入了位數(shù)組編碼和列分塊技術(shù),以降低帶寬需求,進(jìn)一步提高了向量訪問的局部性。而Liu 等人[17]提出的CSR5存儲格式,易于從傳統(tǒng)的CSR格式轉(zhuǎn)換得到,對輸入稀疏矩陣的非零元素分布不敏感。通過采用一種改進(jìn)的分段求和算法實現(xiàn)了基于CSR5的SpMV算法,在跨平臺測試中得到了較高的吞吐量。
RISC-V向量指令集作為向量指令家族中的新晉成員,方興未艾。相關(guān)研究尚處于起步階段,基于RISC-V向量指令實現(xiàn)和優(yōu)化SpMV算法的工作還未有報道,開展此項工作具有重要意義。
本文基于RISC-V向量指令集RV32V,利用其向量寄存器可配置及尋址特性,實現(xiàn)了基于CSR、ELLPACK和HYB壓縮格式的SpMV算法,比較了在稀疏矩陣非零元素不同分布情況下各個算法的計算與存儲效率的變化。同時,針對極度稀疏矩陣每行非零元素數(shù)量波動較大的情況,通過壓縮非零元素密度低的行向量的存儲、調(diào)整HYB分割閾值等手段,改進(jìn)了HYB存儲格式并實現(xiàn)了對應(yīng)的SpMV算法,顯著改善了計算效率和存儲效率。
2 稀疏矩陣存儲格式
2.1 CSR格式
CSR格式是一種比較標(biāo)準(zhǔn)的稀疏矩陣存儲格式,使用3類數(shù)據(jù)來表示:數(shù)值val、列號col和行偏移row。其中,數(shù)值val為非零元素的值,列號col為非零元素的列號,行偏移row表示某行的第1個非零元素在數(shù)值val中的起始偏移位置。對于如式(1)所示的矩陣A,采用CSR格式存儲的結(jié)果如式(2)所示:

(1)
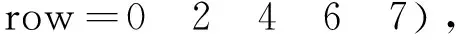

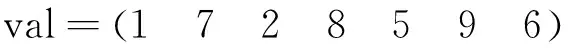
(2)
CSR格式的主要優(yōu)點(diǎn)是對規(guī)則與不規(guī)則稀疏矩陣的存儲都具有穩(wěn)定良好的壓縮比,主要缺點(diǎn)是基于此實現(xiàn)的SpMV算法存在數(shù)據(jù)訪問局部性差、寫沖突和負(fù)載不均衡等問題。
2.2 ELLPACK格式
ELLPACK格式是一種易于向量化的稀疏矩陣存儲格式,使用2個和原始矩陣行數(shù)相同的矩陣來表示:第1個矩陣val存的是數(shù)值,第2個矩陣col存的是列號,行號用自身所在的行來表示。對于行中存在的零元素,可以在val矩陣中填充零元素、在col矩陣中填充11來表示。對于如式(1)所示的矩陣A,采用ELLPACK格式存儲的結(jié)果如式(3)所示:
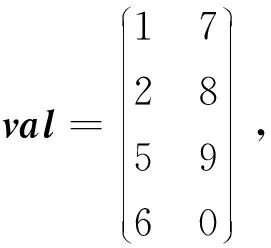
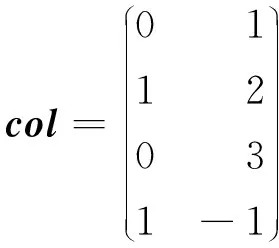
(3)
當(dāng)矩陣中某行的非零元素個數(shù)很多時,ELLPACK格式的存儲效率將急劇下降。
2.3 HYB格式
HYB格式對ELLPACK格式的缺點(diǎn)進(jìn)行改進(jìn),采用COO格式與ELLPACK格式混合的方式對稀疏矩陣壓縮存儲。對每行元素個數(shù)小于閾值的部分采用ELLPACK格式,超過閾值的部分采用COO格式。其中,ELLPACK格式如上所述,需要數(shù)值矩陣val和列號矩陣col存儲,而COO格式使用coo_r、coo_c和coo_v分別存儲元素的行號、列號和值。對于如式(4)所示的矩陣B,采用HYB格式存儲的結(jié)果如式(5)所示:
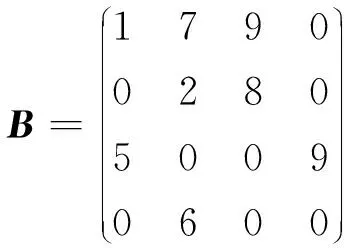
(4)
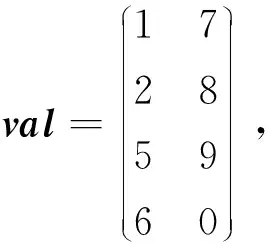

coo_r=(0),
coo_c=(2),
coo_v=(9)
(5)
矩陣B中第1行第3列的元素值為9,行號為0,列號為2,分別存儲于coo_v、coo_r和coo_c中。因此,當(dāng)每行非零元素數(shù)量相差較大時,采用HYB格式可節(jié)約存儲空間,提高存儲效率。
3 SpMV描述、實現(xiàn)與優(yōu)化
3.1 SpMV描述
SpMV可用式(6)描述:
y=A*x
(6)
其中,A為m*n維的稀疏矩陣,x為n* 1維的乘數(shù)向量,y為m* 1維的結(jié)果向量。
為了更好地描述稀疏矩陣,假設(shè)矩陣中每行元素數(shù)量呈正態(tài)分布,正態(tài)分布標(biāo)準(zhǔn)差為σ,均值為μ。
為了表征稀疏矩陣中非零元素的分布特征,使用空行率、稠密度和波動度3個指標(biāo),其定義如式(7)~式(9)所示:
空行率=矩陣全零行數(shù)/矩陣總行數(shù)
(7)
稠密度=非零元素數(shù)/矩陣元素總數(shù)
(8)
波動度=標(biāo)準(zhǔn)差σ/均值μ
(9)
為了表征基于某特定壓縮存儲格式的SpMV算法性能,使用壓縮率和加速比2個指標(biāo),其定義如式(10)和式(11)所示:
壓縮率=壓縮后數(shù)據(jù)大小/原始矩陣大小
(10)
加速比=基于該壓縮格式的SpMV執(zhí)行時間/非壓縮的SpMV執(zhí)行時間
(11)
壓縮率與壓縮效率成反比,壓縮率越小,說明該壓縮存儲格式的壓縮效率越高。
其中,非壓縮的SpMV偽代碼如下所示:
for(inti= 0;i for(intj=0;j y[i]+=A[i*m+j] *x[j]; } } 加速比與計算效率成正比,加速比越大,說明所執(zhí)行的算法計算效率越高。 RISC-V指令集采用模塊化的方式組織,使用一個英文字母表示一個模塊。其中向量指令部分使用“V”表示,32位的RISC-V向量模塊簡記為RV32V。對于32位的RISC-V向量架構(gòu),在執(zhí)行向量乘操作的for循環(huán)時,可以用設(shè)置向量寄存器組的操作作為循環(huán)判斷條件,每次循環(huán)后將當(dāng)前剩余向量長度減去設(shè)置結(jié)果,發(fā)揮向量寄存器可配置的特性,避免了傳統(tǒng)SIMD指令面對計算向量長度非架構(gòu)所支持的向量數(shù)的整數(shù)倍時,需要對剩余尾向量進(jìn)行額外的循環(huán)操作的缺點(diǎn)。例如,對于傳統(tǒng)的擁有固定128位向量寄存器的處理器而言,在處理包含41個32位整型元素的向量時,每次循環(huán)能夠處理的元素個數(shù)為4。10次循環(huán)之后,需要額外循環(huán)處理剩余的1個元素。而在RV32V體系結(jié)構(gòu)中,向量寄存器長度可通過類似vsetvl_e32m8的接口靈活配置,開始待處理向量較長時,使用大的向量寄存器位數(shù),最后向量長度不足時,將向量寄存器長度設(shè)置為合適值,充分簡化了代碼編寫,提高了程序效率。 在實現(xiàn)矩陣運(yùn)算時,常用的向量操作包括間隔向量尋址、索引向量尋址、向量乘加和向量標(biāo)量乘等,如圖1所示。 Figure 1 Vector operations of RV32V圖1 RV32V向量操作示意圖 基于RV32V,充分利用RISC-V向量寄存器可配置和尋址的特點(diǎn),本文分別實現(xiàn)CSR、ELLPACK和HYB存儲格式的SpMV算法。向量化SpMV算法實現(xiàn)總體可分為索引計算、乘數(shù)加載、向量相乘、結(jié)果回寫和指針偏移這幾個步驟,下面結(jié)合偽代碼分別描述各壓縮格式的RISC-V向量化SpMV實現(xiàn)。 基于CSR格式的RISC-V向量化SpMV偽代碼如下所示: 輸入行偏移指針row_p;row_p數(shù)組長度m;坐標(biāo)指針col_idx;值指針val;向量指針x。 輸出結(jié)果向量指針y。 1:vfloat32m8_tvec_a,vec_b,vec_c; 2:vuint32m8_tindex; 3:float *a=val,*b=x,*c=y; 4:whilevl=vsetvl_e32m8(col)do 5:vec_a=*(vfloat32m8_t *)a; 6:index=*(vuint32m8_t *)col_idx; 7:index=vfmul_vf_f32m8(index,4); 8:vec_b=vlxe_v_f32m8(b,index); 9:vec_c=*(vfloat32m8_t *)c; 10:vec_c=vfmadd_vv_f32m8(vec_a,vec_b,vec_c) 11: *(vfloat32m8_t *) c=vec_c; 12:c+=vl;a+=vl;b+=vl; 13:col_idx+=vl;col-=vl; 14:endwhile 15:returny. 首先對列號col_idx數(shù)組進(jìn)行順序?qū)ぶ罚嬎愠鏊饕?如第6、7行所示;然后根據(jù)計算出的索引,在乘數(shù)向量x中進(jìn)行索引尋址,加載第1個向量乘數(shù),并對數(shù)值val數(shù)組順序?qū)ぶ罚虞d第2個向量乘數(shù),如第8、9行所示;最后2個向量乘數(shù)中各元素依次相乘,結(jié)果回寫暫存,如第10、11行所示。進(jìn)行指針偏移準(zhǔn)備下一輪計算,如第12、13行所示。依次循環(huán)往復(fù)直到計算完成。 基于ELLPACK格式的RISC-V向量化SpMV偽代碼如下所示: 輸入坐標(biāo)指針col_idx;值指針val;值矩陣長度m;值矩陣寬度col;向量指針x。 輸出結(jié)果向量指針y。 1:vfloat32m8_tvec_a,vec_b,vec_c; 2:vuint32m8_tindex; 3:float *a=val,*b=x,*c=y; 4:fori=0 tocoldo 5:num=m;a=val+i*col; 6:b=x;c=y+i*col; 7:col_idx=col_idx+i*col; 8:whilevl=vsetvl_e32m8(num)do 9:vec_a=*(vfloat32m8_t *)a; 10:index=vlse_v_f32m8(col_idx,col*4); 11:index=vfmul_vf_f32m8(index,4); 12:vec_b=vlxe_v_f32m8(b,index); 13:vec_c=*(vfloat32m8_t *)c; 14:vec_c=vfmadd_vv_f32m8(vec_a,vec_b,vec_c); 15: *(vfloat32m8_t *)c=vec_c; 16:c+=vl;a+=vl;b+=vl; 17:col_idx+=vl;num-=vl; 18:endwhile 19:endfor 20:returny. 向量化計算過程中,首先對列號col數(shù)組間隔尋址,間隔為每行字節(jié)數(shù),按列順序獲取向量,如第10行。對得到的向量值做向量標(biāo)量乘法,轉(zhuǎn)化為字節(jié)數(shù),計算出索引,如第11行;然后根據(jù)計算出的索引,在乘數(shù)向量x中進(jìn)行索引尋址,加載第1個向量乘數(shù),如第12行;接著對數(shù)值val數(shù)組順序?qū)ぶ罚虞d第2個向量乘數(shù),如第13行;最后向量元素依次相乘,如第14行,結(jié)果回寫暫存,如第15行。指針偏移準(zhǔn)備下一輪計算,如第16、17行,依次循環(huán)往復(fù)直到計算完成。 對基于HYB格式的向量化SpMV可以分為ELLPACK和COO 2部分,其中ELLPACK部分與上述基于ELLPACK格式的RISC-V向量化過程相同,COO部分的向量化過程與CSR格式的類似。 基于HYB格式的RISC-V向量化SpMV偽代碼(COO部分)如下所示: 輸入行坐標(biāo)指針col_r;列坐標(biāo)指針coo_c;值指針val;長度num;向量指針x。 輸出結(jié)果向量指針y。 1:whilevl=vsetvl_e32m8(num)do 2:vec_a=*(vfloat32m8_t *)a; 3:index=*(vuint32m8_t *)coo_c; 4:index=vfmul_vf_f32m8(index,4); 5:vec_b=vlxe_v_f32m8(b,index); 6:vec_c=*(vfloat32m8_t *)c; 7:vec_c=vfmadd_vv_f32m8(vec_a,vec_b,vec_c); 8: *(vfloat32m8_t *) c=vec_c; 9:c+=vl;a+=vl;b+=vl; 10:col_index+=vl;num-=vl; 11:endwhile 12:returny. 首先對列號col數(shù)組順序?qū)ぶ罚绲?行,得到的向量值做向量標(biāo)量乘法,如第4行,計算出索引;然后在乘數(shù)向量x中進(jìn)行索引尋址,加載第1個向量乘數(shù),如第5行;接著對數(shù)值val數(shù)組順序?qū)ぶ罚虞d第2個向量乘數(shù),如第6行;最后向量元素依次相乘,如第7行,結(jié)果回寫暫存,如第8行。指針偏移準(zhǔn)備下一輪計算,如第9、10行。依次循環(huán)往復(fù)直到計算完成。 HYB格式使用ELLPACK格式和COO格式混合的方式,以更緊湊的方式存儲擁有非零元素密度大的行的稀疏矩陣,提升了存儲效率。圖2給出了矩陣C的HYB格式存儲結(jié)果。將第1行和第2行的元素5存儲為COO格式,使所需的存儲空間從60(6*5*2)個整型大小降低到54(6*4*2+6)個整型大小。 Figure 2 Storage diagram based on HYB format圖2 基于HYB格式的存儲示意圖 但是,行之間非零元素相差很大的情況不僅表現(xiàn)在擁有非零元素密度大的行,同時也體現(xiàn)在擁有非零元素密度小的行。基于這一點(diǎn),本文提出改進(jìn)的HYB格式IHYB(Improved HYB format)。IHYB格式對非零元素密度低于IHYB分割閾值的行也使用COO格式存儲。此時ELLPACK格式所存儲元素的行號不能用自身所在的行來表示,于是引入bitarray數(shù)組記錄ELLPACK格式中每行元素在原始矩陣中的行號。對于HYB格式,在假設(shè)完全填充的ELLPACK格式計算速度比COO格式快3倍的情況下,通過經(jīng)驗法則選擇數(shù)值K作為ELLPACK和COO之間的分割值,使得矩陣中具有K個以上非零元素數(shù)的行數(shù)不少于M/3,其中M是矩陣總行數(shù)[13]。而對于IHYB格式,參照類似規(guī)則,閾值的確定使用迭代算法1。 算法1確定IHYB分割閾值的算法 輸入:稀疏矩陣每行非零元素數(shù)。 輸出:IHYB分割閾值。 Step1對稀疏矩陣每行元素數(shù)中的非零值從小到大排序,找到2/3分位點(diǎn)作為HYB閾值。 Step2將HYB閾值/4作為IHYB分割閾值。 Step3去除非零元素數(shù)低于IHYB分割閾值的行,按照Step 1更新HYB閾值。 Step4將更新后的HYB閾值/4作為最終的IHYB分割閾值。 如HYB使用的經(jīng)驗參數(shù),IHYB閾值中使用的參數(shù)2/3,1/4等,也是通過經(jīng)驗法則確定。閾值的兩步迭代求解操作開銷包括對稀疏矩陣的2次遍歷(統(tǒng)計每行非零元素數(shù)時)和每行非零元素數(shù)大小的排序。矩陣遍歷可以在壓縮存儲格式的轉(zhuǎn)換過程中完成,并不增加額外開銷。假設(shè)稀疏矩陣有m行k列,排序的復(fù)雜度為m*logm,一般而言不會超過矩陣元素數(shù)m*k,可以忽略。因此,通常來說,閾值求解過程的開銷并不會影響算法性能。 圖3給出了圖2中矩陣C的IHYB格式存儲結(jié)果。第6行的元素1也存儲為COO格式,同時bitarray數(shù)組指示了矩陣value中每行元素的行號,使所需的存儲空間從HYB的54(6*4*2+6)個整型大小進(jìn)一步降低到45(4*4*2+4+9)個整型大小。 Figure 3 Storage diagram based on IHYB format圖3 基于IHYB格式的存儲示意圖 本文實驗使用Spike模擬器[18]環(huán)境,其中DCache設(shè)置大小為32 KB,ICache大小為32 KB,L2 Cache大小為128 KB,CPU主頻1 GHz,內(nèi)存使用4 GB。限定矩陣規(guī)模為4 KB,矩陣每行非零元素個數(shù)滿足正態(tài)分布,以空行率、稠密度和波動度控制稀疏矩陣非零元素分布特性,以壓縮率和加速比衡量算法的空間效率和時間效率。 固定空行率為0.3,波動度為0,改變稠密度觀察稀疏矩陣稠密度對SpMV算法性能的影響。隨著稠密度增加,非零元素數(shù)量也增加,各算法所需存儲空間增加,計算時間增多,因此,加速比減小,壓縮率升高。整體上由加速比衡量的計算效率由高到低為CSR、IHYB、HYB和ELLPACK,如圖4所示。由壓縮率衡量的存儲效率由高到低為IHYB、CSR、HYB和ELLPACK,如圖5所示。由圖4可知,當(dāng)稠密度超過0.08時,CSR的計算效率降低,IHYB的加速比反超CSR。原因在于CSR的段累加求和部分難以被向量化,當(dāng)非零元素數(shù)量較多時,計算效率受到影響開始下降。得益于較高的壓縮效率和較好的向量化程度,IHYB的加速比表現(xiàn)優(yōu)異。而ELLPACK中存儲了大量零元素,導(dǎo)致整體計算效率較低。 Figure 4 Effect of density on speedup圖4 稠密度對加速比的影響 Figure 5 Effect of density on compressibility圖5 稠密度對壓縮率的影響 固定空行率為0.3,稠密度為0.08,改變波動度觀察稀疏矩陣波動度對SpMV算法性能的影響。圖6和圖7別顯示了波動度對加速比和壓縮率的影響。隨著波動度增大,IHYB、HYB和ELLPACK的壓縮率不同程度增大,加速比不同程度減小,而CSR的壓縮率和加速比基本保持穩(wěn)定。由圖6可知,隨著波動度增大,ELLPACK的加速比迅速降低。原因在于波動度的增大導(dǎo)致ELLPACK格式壓縮率迅速升高,存儲效率降低,這點(diǎn)由圖7也可以看出。存儲的無效零元素大量增加,進(jìn)一步導(dǎo)致ELLPACK格式的計算效率下降,加速比走低。與ELLPACK格式不同的是,其他3種格式壓縮率較為穩(wěn)定。由圖7可知,CSR的壓縮率最為穩(wěn)定,基本不受波動度影響,HYB和IHYB的壓縮率隨著波動度增大緩慢增加,并且IHYB在壓縮效果上好于HYB格式。波動度低于0.2時,IHYB的存儲效率表現(xiàn)甚至好于CSR。由圖6可知,很大程度得益于此,在波動度低于0.2時,IHYB的計算效率也高于CSR。 Figure 6 Effect of volatility on speedup圖6 波動度對加速比的影響 Figure 7 Effect of volatility on compressibility圖7 波動度對壓縮率的影響 圖8和圖9分別進(jìn)行了HYB格式和基于HYB格式改進(jìn)的IHYB在不同波動度下,加速比和壓縮率的對比。平均而言,相比HYB格式,IHYB格式在加速比上提升了13%,壓縮率上降低了6%。壓縮率的降低趨勢和加速比的提升趨勢一致,從而體現(xiàn)了壓縮效率的提高導(dǎo)致計算效率隨之提高的規(guī)律。 Figure 8 Comparison of speedup between HYB and IHYB圖8 HYB和IHYB的加速比對比 Figure 9 Comparison of compressibility between HYB and IHYB圖9 HYB和IHYB的壓縮率對比 SpMV算法在科學(xué)計算中占有重要地位,實現(xiàn)并優(yōu)化基于RISC-V向量指令的SpMV算法也具有重要價值。本文首次利用RISC-V向量寄存器可配置性和向量尋址模式,結(jié)合CSR、ELLPACK和HYB存儲格式的特點(diǎn),實現(xiàn)了對應(yīng)的SpMV算法。在仿真環(huán)境下比較了各SpMV算法面對不同非零元素分布的稀疏矩陣,表現(xiàn)出的計算效率和存儲效率差異。同時,針對HYB格式,提出了更為緊湊、穩(wěn)定的改進(jìn)格式IHYB。實驗顯示,在非零元素分布變化時,基于IHYB格式實現(xiàn)的SpMV表現(xiàn)出更為優(yōu)異的存儲效率和計算效率。但是,目前實現(xiàn)的算法都是基于單個RISC-V核心的。面對更為復(fù)雜的RISC-V多核處理器或異構(gòu)計算環(huán)境,如何充分發(fā)掘算法中的并行性,提高并行度,將是一個更為復(fù)雜深刻的挑戰(zhàn)和命題。3.2 RISC-V向量指令集RV32V
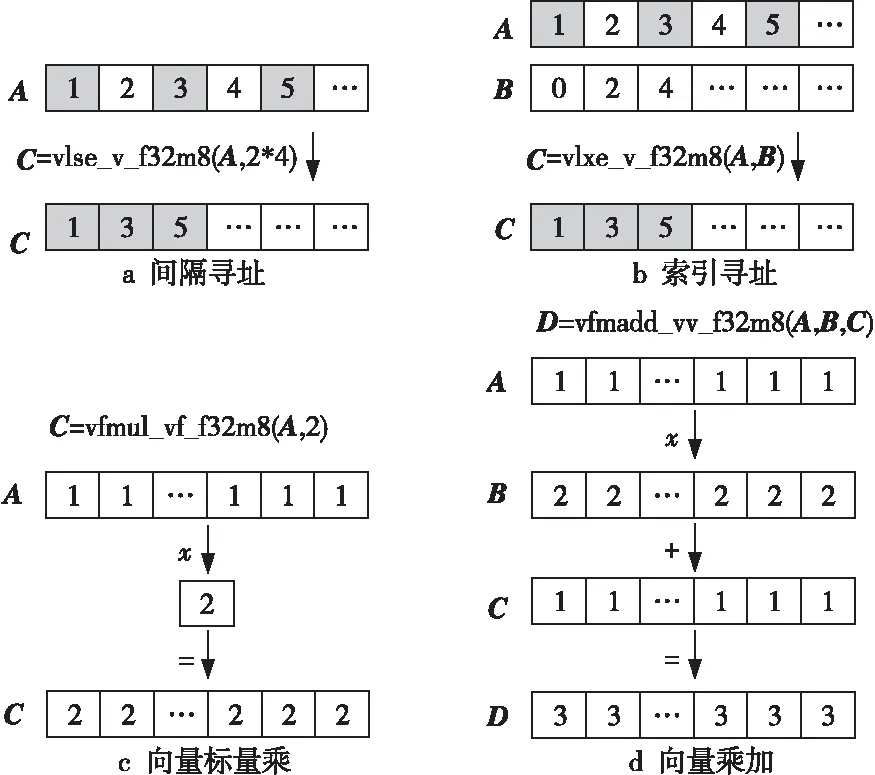
3.3 基于RV32V與傳統(tǒng)壓縮格式的SpMV實現(xiàn)
3.4 基于 HYB格式的改進(jìn)


4 算法測試與分析
4.1 稠密度的影響
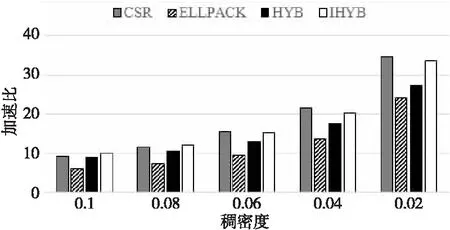
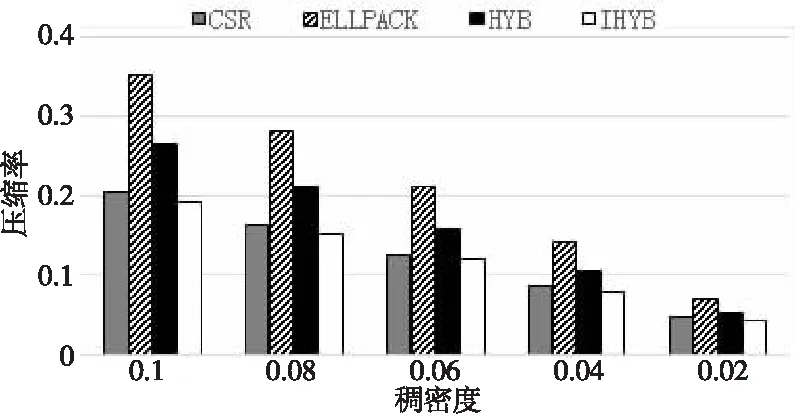
4.2 波動度的影響

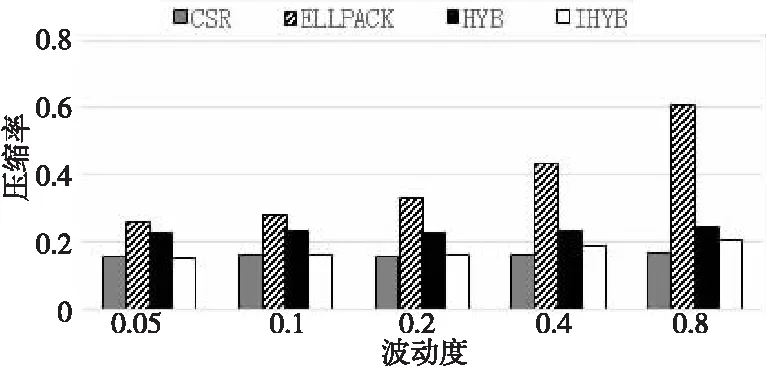
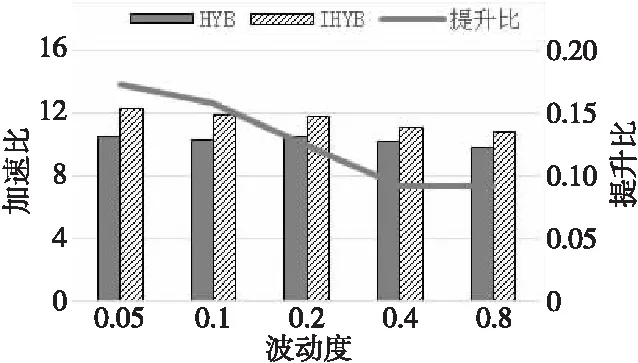

5 結(jié)束語

