量子視角下的智能優化算法綜述

王 鵬，王 方

(1.西南民族大學計算機科學與工程學院 成都 610225；2.廣東省國產服務器工程技術研究中心 廣州 510535；3.中國科學院成都計算機應用研究所 成都 610041；4.中國科學院大學 北京 石景山區 100049)

量子力學誕生于20 世紀初，是在Einstein、Bohr、Schr?dinger、Heisenberg 等一大批天才的物理學家的共同努力下建立起來的，這是人類歷史上少有的由科學家群體共同努力建立的科學理論框架[1-2]。量子力學打破了人們從宏觀世界獲得的確定性世界觀“常識”，為我們描述了一個被概率和不確定性統治的微觀世界。物質世界的運動規律本質上是概率化的，電子雙縫實驗、波函數和不確定性關系等量子力學中的實驗和理論都在不斷地證明這一結論。量子力學揭示了物質世界本質的運動規律并被應用于各個技術領域，成為現代科學和技術的基石。同時量子力學的普遍適用性也在不斷地得到證明，量子技術已成為一個國家科技實力的標志性技術，是繼云計算、大數據、人工智能、區塊鏈技術之后，我國未來的一個新的戰略性新興技術領域。

不少文章在表述量子算法時都有所混淆。算法主要概括為兩種：1)采用物質的量子效應制造的量子計算機及其在上面運行的算法。這種算法主要又包括兩類，一類是基于量子門的量子計算機及其算法[3-6]，另一類是基于量子退火原理的量子退火計算機及其算法[7-10]。其中量子退火計算機并不是通用量子計算機，它主要用于對優化問題的求解[11-12]。2)借鑒量子力學中的一些概念，如量子比特、量子門，將這些概念用于改進現有算法性能。這類算法還是運行在經典計算機上的，其所使用的量子特性可被認為僅僅是一種數學上的操作。本文所介紹的優化算法指的是后一種運行在經典計算機上的優化算法。

由于優化算法具有廣泛的應用場景，經過長期發展，經歷了百花齊放的過程。量子理論中的一些觀點和方法在優化算法中也得到過成功的應用，但優化領域一直面臨缺乏完備理論支持的問題，大量的優化算法模型特別是自然模型都在從各自的視角對優化算法進行解釋。但由于這些自然模型往往缺乏完備的數學框架，所以一些自然模型所提出的理論框架事實上是人為“杜撰”的。量子力學是描述大自然最基礎、最本質規律的一門學科，同時量子力學通過長期的發展已具備了完備的數學框架并被大量的實驗所證明[13-14]，因此，將量子力學作為描述優化算法的物理模型是可行的。

量子視角下的智能優化算法研究有兩個方向：

1) 將量子計算中一些概念和數學機制應用于已有的優化算法，其目的是提升現有算法的性能。如量子遺傳算法(quantum-inspired genetic algorithms,QGA)利用量子位和量子疊加態對染色體進行編碼，使一個染色體表示多個狀態的信息的同時使用量子旋轉門對種群進行更新，以當前最優個體的信息為引導進化[15]。在迭代過程中，每個量子位的疊加態將會塌縮到一個確定的狀態，從而趨于穩定和達到收斂，最后實現尋優的目的。量子蟻群算法(quantum ant colony algorithm,QACA)將量子計算和蟻群算法相結合，把量子計算中的態矢量和量子旋轉門引入到蟻群算法中，加速了算法的收斂速度[16]。量子人工魚群算法(quantum artificial fish school algorithm,QAFSA)用量子計算的方法重新描述了人工魚的行為，用量子比特對人工魚進行編碼，用量子旋轉門實現人工魚的更新操作，用量子非門進行人工魚變異，從而實現了目標的優化求解[17]。該方向應用量子理論的目的不是為了解釋智能優化算法，而只是單純地將量子力學中的一些方法作為提升算法性能的手段。由于量子力學描述的是一個概率化的微觀世界，量子機制通常都是概率化的，該方向的工作證明量子機制在智能優化算法中常常是有效的。目前在智能優化算法中使用的量子比特并不試圖從量子力學的角度對智能優化算法做出解釋，而僅被作為一種可以借鑒的編碼機制。

2)基于智能優化算法和量子力學在概率行為上的相似性，將優化問題的目標函數視為量子系統中的約束勢能，從而將優化問題轉化為求量子系統的基態波函數問題。第二個方向的特點是將優化問題從模型上視為量子問題，這樣量子力學的整個數學框架就能被應用于對智能優化算法的研究和分析，得到智能優化算法迭代過程中的基本動力學規律和基本操作。量子退火算法(quantum annealing algorithm,QAA)是這個研究方向的先驅，其利用Schr?dinger 方程，對優化問題進行了初步的建模，提出了勢能?優化問題等效的概念，量子退火算法利用量子力學的隧穿效應，在尋找全局最小值時更快地穿過局部極值點旁的勢壘從而找到最優或接近最優的解[18]。多尺度量子諧振子算法(multi-scale quantum harmonic oscillator algorithm,MQHOA)也使用Schr?dinger 方程[19]，將優化過程轉換為在諧振子勢約束下的多尺度退火過程[20]，利用多尺度的概念，實現了量子擾動的逐步減小和優化系統對基態能量的逼近。這樣利用Schr?dinger方程構建優化模型的方法還有量子粒子群算法(quantum-behaved particle swarm optimization,QPSO)，其利用Delta 勢阱的假設，假設PSO 粒子群在虛擬的約束條件下運行，構建了其模擬量子優化系統[21-22]。

從當前研究情況來看，基于量子比特的智能優化算法研究已進行得相對充分，其主要應用場景是性能改進領域。而采用量子力學對智能優化算法進行建模，并利用量子力學的數學體系對智能優化算法進行研究目前尚處于初級階段，是今后一個非常有前途的研究方向，將對解決智能優化算法領域當前的一些挑戰具有建設性的作用。

本文結合智能優化算法的最新研究進展，對量子力學在智能優化算法中的應用進行綜述。介紹了從基于量子比特的智能優化算法向智能優化算法的量子動力學發展的過程，重點對智能優化算法量子動力學當前取得的一些研究結果進行了介紹，并展望了未來的研究方向。

1 智能優化算法當前面臨的挑戰

優化問題是一類常見問題，在實際工程應用中有大量的問題都可被抽象為優化問題。求函數的最小值、尋找最優路線和神經網絡算法中獲得最優的連接權重值等，都可被視為優化問題。

以函數優化為例，從數學的角度，一維函數優化問題可以定義如下：

針對目標函數f(x)在 實數定義域 [a,b]上的優化問題，找到一個實數x0∈[a,b]，對于任意x∈[a,b]，滿足f(x0)≤f(x)，則稱x0為目標函數在實數定義域[a,b]的全局最優解。

以上定義是數學上對優化問題的一個確定性的定義。數學上的優化問題是要從理論上找到x0這一個確定的全局最優解。而從算法的視角來看函數優化問題則是將目標函數假設為黑盒。黑盒假設認為：目標函數的表達式f(x)是未知的，智能優化算法只能通過采樣確定從目標函數定義域集合到值域集合中的每一個映射。每一次采樣就是對黑盒進行的一次測量，測量的次數越多所獲得的目標函數信息也越多。由于通常無法對目標函數定義域進行遍歷，所以智能優化算法對目標函數f(x)全局最優解的位置的測量結果是不確定的，算法在運行過程中并不知道它是否找到了全局最優解。

回顧經典計算機上的智能優化算法的歷史，其發展經歷了一個黃金時期，遺傳算法[23]、退火算法[24]、蟻群算法[25]和粒子群算法[26]等經典的方法都在這一時期被提出，并很快被廣泛地應用于各個領域。隨后，針對這些經典智能優化算法的改進研究也成為了該領域的研究熱點，這使智能優化算法的性能得到了快速的提升，并開始向高維大規模問題進行挑戰。受前期經典智能優化算法構造思路的啟發，許多算法研究者不斷地采用新的啟發式模型并據此不斷提出新的方法。很快智能優化算法領域變得百花齊放，每一個性能優良的新智能優化算法后面都有一批跟進的研究者，并形成一個又一個的研究團體和派別，此時智能優化算法的研究進入了鼎盛時期。

然而智能優化算法研究的隱憂卻也在逐漸顯現出來，總結為以下兩點：

1) 大量的智能優化算法模型來自于對自然現象的模擬，在理論分析時很難為這些復雜的體系建立完備的理論模型，這阻礙了對智能優化算法的深入研究；

2) 不同的智能優化算法中存在著同質化的機制和操作。如很多算法都采用了均勻采樣或正態采樣，抑或是多尺度行為，但卻由于算法模型的不同被割裂地解釋為不同的原理。

這些問題已被一些優化領域的學者注意到了。文獻[27]提出“現在優化計算領域的研究，重要的不是提出新的算法而是為優化算法建立普遍適用的規則和策略，研究優化問題和優化算法中的共性問題”。文獻[28]提出“不鼓勵大家再提出新的優化算法，這些新算法可能只會分散解決優化中真正具有挑戰性和真正重要問題的注意力”。因此，有研究者認為當前大量的新算法是對舊算法的新偽裝，并認為這一時代即將結束[29-30]。這時需要更深刻地去認識優化問題，解釋智能優化算法的基本操作和核心迭代過程，避免在漫無目的的探索中去提出各種所謂的新算法，這可能是當前智能優化算法研究的一個重要方向。

2 選擇量子力學

量子力學所描述的是被概率所統治的世界圖像，而智能優化算法在不確定性算法的基礎上大量地在使用概率化的搜索行為。這使得量子力學所描述的世界體系與智能優化系統在概率上存在著一定的相似性，這正是采用量子力學視角對智能優化算法進行研究的基礎。事實上，量子力學對現代計算機技術的發展有著深刻的影響，不少計算機科學的開創者都在研究量子力學，甚至還為量子力學做出過巨大貢獻。現代計算機之父von Neumann 寫出了《量子力學的數學基礎》[31]，1931 年Turing 認真研讀了這本書。而且早在1929 年，Turing 還著迷于天文學家Eddington 所著的《物理世界的本質》[32]，Eddington 也認為“大腦也是由原子、電子組成的，量子物理或許能為人類意識、思維提供產生的機會和空間”。

1926 年Schr?dinger 提出了量子力學中最為著名的方程——Schr?dinger 方程：

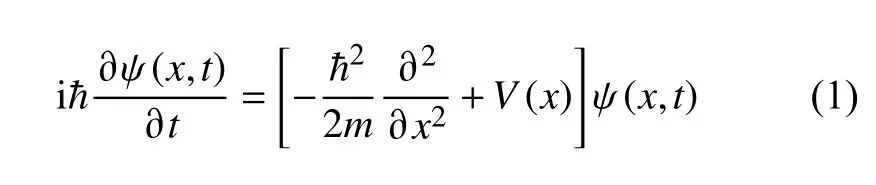
式中，V(x) 為 勢能；ψ (x,t)為波函數。1927 年，Born給出了Schr?dinger 方程中波函數的概率解釋[33]，他認為波函數代表了微觀粒子的概率分布，而且波函數也完整地表達了一個微觀粒子的運動狀態。Born的解釋建立了波函數與概率分布之間的關系，揭示了一個由概率行為所統治的微觀世界。

量子力學在Born 的概率解釋下與智能優化算法搜索過程中的隨機性存在著深刻的內在聯系。這一點提示我們采用量子理論的視角對優化問題和智能優化算法進行建模是一種可行的思路。隨機性也是計算機智能產生的根源之一，文獻[34]指出“隨機性的程度決定了智能的高低”，這一論斷指出了智能的本質是隨機性。包括人類的智能也來自于隨機性，一個充滿了隨機性的世界通過長期演化才出現了人類。1976 年，圖靈獎獲得者Rabin 認為“應該放棄的只是以完全確定的方式獲得結果，這種結果可能出錯，然而出錯的可能性微乎其微，也就是說可以把概率算法用到這類問題中來”。Rabin 的論斷可以理解為以犧牲確定性來獲得較高的計算效率，他從技術層面給出了實現智能的方法就是放棄對確定性的追求。現代人工智能算法幾乎無一例外的采納了Rabin 的建議，這說明越來越多的學者認識到智能產生于隨機性。而由量子力學所描述的物質世界的本質運行規律正好是概率化的，采用量子力學對智能優化算法進行研究是基于自然哲學的本質要求。2018 年11 月李國杰院士在《中國計算機學會通訊》上發表了題為《計算機科學基礎理論需要重塑》的卷首語，他指出“量子力學改變了傳統的邏輯定義，把概率看成了邏輯的內在組成。在計算機領域，構造一臺完全公理化驅動的自動機也不現實，而對復雜環境，需要放棄嚴格邏輯而改用概率邏輯”。正如著名量子物理學家Feynman 所說：“自然不是經典的，如果你想模擬自然，你最好把它變成量子力學。”而且 Feynman也最早指出了量子計算機的可行性，開啟了量子計算時代[35]。對于量子力學在智能優化算法中的應用不應只是停留在借鑒層面，由于優化問題和智能優化算法自身的概率特性，智能優化算法的迭代過程或可能被量子理論的基本規律所描述。

3 隱含并行性

研究量子視角下的智能優化算法，可以先從隱含并行性開始。量子力學中的概率機制所帶來的不確定性正是用量子模型來描述智能優化算法的原因。隱含并行性的起源也是來自于不確定性，這或許也是智能算法所具有的解空間高速搜索能力的原因。雖然量子智能優化算法研究的是經典計算機上的智能優化算法，但由不確定性造成的隱含并行計算能力也是不應該回避的話題。

各類智能優化算法獲得高效的解空間搜索能力的原因都是在某種程度上犧牲了對解的確定性的要求。如果要求以100%的概率找到最優解則只能使用強力搜索，這在大多數復雜優化問題中是不可能實現的。因此幾乎所有的智能優化算法都不同程度地使用了隨機數和概率策略，這些策略的引入使智能優化算法能在可以接受的時間內獲得準確度可以接受的解。這種搜索速度提高的現象被稱為算法的隱含并行性(implicit parallelism)。

算法的隱含并行性有別于算法的內在并行性(inherent parallelism)。內在并行性是指算法本身非常適合大規模并行，可以同時讓幾百甚至數千臺計算機各自獨立進行計算，運行過程中基本不做任何消息通信。對于隱含并行性在其他智能優化算法中的情況，目前的研究資料還極度缺乏，其實這是一個十分重要的研究課題，它涉及到了智能算法的內在核心問題，但由于本身問題的理論困難，研究一直相對緩慢。

隱含并行性的研究開始于20 世紀70 年代，目前對隱含并行性的研究多集中于遺傳算法。1975年文獻[36]首次提出了隱含并行性的概念，并指出隱含并行性是遺傳算法能夠快速有效搜索的根本原因。雖然隱含并行性是廣泛存在于智能算法中的一個重要特性，但有關其他智能算法隱含并行性的研究長期以來沒有得到國內外學者的重視。

根據文獻[36]定義的隱含并行性，結構重組等遺傳操作可以使被采樣的模式數盡可能的多，這樣可以帶來較大的隱含并行性。遺傳算法每代雖然只處理了N個個體，但隱含處理的模式數遠遠大于N。針對這一定義，文獻[37]指出遺傳算法每代雖然只顯示處理N個個體串，實際隱含處理的模式數下界為，其中c1為 一個小整數，l為串長。這一下界表明模式數和N3成正比，也就是說遺傳算法每代雖然只顯示處理N個個體串，但是隱含處理了至少N3個模式。遺傳算法這種隱含處理能力正是該算法在解空間快速搜索的原因，隨后其他學者對這一結論展開了進一步研究[38-41]。遺傳算法[42]在這一結論的基礎上進一步證明了隱含處理的模式數的下界為緊下界。國內有關隱含并行性的研究也是針對遺傳算法進行的，文獻[43]進一步研究了遺傳算法隱含處理的模式數，給出了對任意串長l及群體規模N，在等概率抽取每個群體的條件下，遺傳算法每代所處理的模式長度不超過ls的不同模式期望數的精確表達。文獻[44]給出了每代至少產生O(2N?1)數量級的新模式。

1975 年Rabin 等人提出的檢測素數的不確定性方法Miller-Rabin 檢測法正是一種以犧牲確定性來獲得快速檢測素數的方法。Miller-Rabin 檢測法對待檢測數n進 行k次試驗所需的時間為O(log3n)，而出錯的概率不超過1 /2k。目前這一素數檢測方法也是檢測素數最快的方法之一，其本質上也是通過犧牲確定性構造出具有隱含并行性的算法，其獲得的隱含并行計算能力也是指數級的。

文獻[45]從遺傳算法和模擬退火算法的隱含并行性入手，利用物理學中的不確定性原理以及熱力學中的熵對隱含并行性進行分析，指出算法隱含并行性的根源是不確定性和高熵態。文獻[46-47]分析了隱含并行性與不確定性的關系，并從哲學角度對不確定性進行了分析。研究表明隱含并行性是智能算法中普遍存在的重要機制。隱含并行性的研究結果為智能優化算法的設計指出了一個重要的原則：犧牲算法確定性可能獲得更好的計算效率。由于隱含并行性可能是指數級的，因此這種確定性的犧牲在算法實踐中是可以接受的，事實上大多數的智能優化算法和智能算法都不同程度地采用了這種策略。

總之，隱含并行性作為一種反映算法內在快速搜索能力的指標一直以來未被研究者所重視。算法隱含并行性至今還沒有嚴格的數學定義，特別是不確定性與隱含并行性之間的對應關系還未得出結論，相關研究工作主要也還是針對遺傳算法在進行。近年來算法隱含并行性的研究更是處在停頓狀態，幾乎無法檢索到相關論文，國內的研究者更是寥寥，這個非常重要的研究方向被大家所忽略了。

4 基于量子比特的智能優化算法

算法的隱含并行性要求一個算法要構造一個具有概率特性的算法結構和算法操作，量子力學所具有的天然的概率特性成為了描述和研究優化問題的一個有力的理論武器。量子力學中的粒子可以處于多種本征態的疊加態，這是量子力學所描述的一種非常奇特的現象，最有名的思想實驗就是Schr?dinger 的貓，量子疊加態在經典世界是非常難以理解的。量子比特是量子疊加態原理的一種特殊情況，如果一個量子系統只有兩個狀態，采用Dirac 算符分別用 |0〉和 |1〉來表示這兩個狀態，它可以用來描述一個基于二進制編碼的系統。在經典計算機中一個bit 只能是0 或1，也就是說只能處于|0〉態和|1〉態。而在量子系統中一個量子比特可以處于兩種狀態的疊加，即：

式中，α 和 β 是分別處于兩種態的概率幅，α2+β2=1。狀態φ 既不是0 也不是1，而是處于0 和1 的疊加態。在對這種疊加態進行觀察時會按概率坍縮到其中一個態。

量子比特這一概念是智能優化算法設計時常采用的一個機制。最早應用這一機制的是遺傳算法，1996 年文獻[15]提出了量子遺傳算法(quantuminspired genetic algorithms,QGA)求解旅行商問題，并將這一算法稱為量子啟發式算法，他們借鑒了量子疊加原理構造了一個具有“多宇宙”的策略，可以認為是一個多種群的策略。

2000 年，文獻[48]提出遺傳量子算法，采用量子比特的概念提高對背包問題的求解能力，量子比特提高了算法的隨機性，對于算法的全局搜索能力是有益的。2002 年文獻[49]將算法的名稱改為量子進化算法(quantum-inspired evolutionary algorithm,QEA)，完整的結果發表在TEVC 雜志上。他們的基本思路是將量子比特的概念與遺傳算法的基本操作相結合，采用量子比特來改造遺傳算法二進制編碼機制，使遺傳算法的經典二進制編碼串成為量子比特串。通過量子比特改造的具有n位長度的遺傳算法二進制編碼可以表示為：

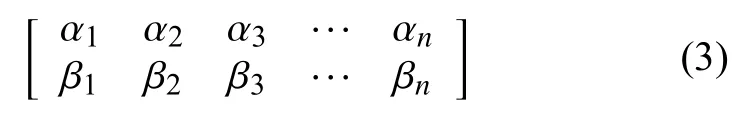
與經典的二進制表達相比，量子比特使二進制串的不確定性大大增加。如果采用量子比特所構成的串并對其進行多次測量，則任意一個可能解都會以一定的概率出現。如具有3 個量子比特的量子串為：

這個串是由3 個量子比特構成：

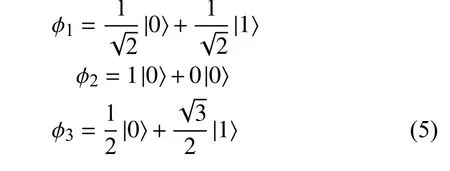
量子比特所構成的量子比特串擁有強大的表達力，它蘊含了所有解出現的概率。假設最優解為二進制串101，則其在測量過程中出現的概率為，也就是說量子比特串中以一定概率隱含最優解。量子比特串使確定性的二進制串變成了解的概率疊加，從而大大增加了算法迭代過程中解的不確定性。對于長度為n的量子比特串的任何操作等效于對 2n個不同經典比特串的操作。

量子比特在理論和實踐上的成功使不少研究者進入這一領域，構造出了一批基于量子比特的量子智能優化算法。2007 年同樣采用量子比特機制的量子蟻群算法被提出[16]，2010 年量子魚群算法被提出[17]，文獻[50-51]也將量子比特用于免疫克隆算法中并提出了量子免疫克隆算法。

這一類基于量子比特的算法是將量子比特的數學框架作為一種通用手段應用于已有的算法，以提高已有算法的性能，特別是全局搜索性能。由于量子比特的引入必然會增加算法迭代過程中的不確定性，從而使迭代過程不易陷入局部最優。理論上這對基礎算法效果的改進是可行的，但這類研究并未從智能優化算法本身量子特性的角度來考慮，因此無法依據量子力學的知識獲得智能優化算法的核心基礎操作。

5 量子退火算法與優化問題的量子可描述性

采用量子比特來構造量子計算機和智能優化算法是基于對經典計算機的慣性認識，量子計算不一定要采用基于比特的邏輯運算來實現。在量子計算領域中，優化問題是被解決得最好的，這得益于優化問題可以有效的被量子模型所描述。量子退火理論及量子退火計算機的出現為這一問題提供了確切的證據。

1994 年文獻[52]提出可以將優化問題的目標函數f(x)視 為量子系統中的勢能V(x)(稱為勢能等效關系，equivalence of potential energy,EPE)，即V(x)=f(x)，從而可以通過量子退火過程或擴散蒙特卡羅方法(Diffusion Monte Carlo,DMC)來獲得系統的基態[52]。如果將勢能等效關系條件下量子系統的基態視為優化問題的解，則該工作從理論上證明了智能優化算法的迭代過程演化可以采用含時Schr?dinger 方程來描述。并認為量子退火與經典退火的不同之處在于量子退火通過量子隧道效應在優化過程中實現跳出局部最優，并且隧道效應的大小與量子系統的質量有關，這一點指出了智能優化算法的多尺度過程。文獻[52]還采用這一方法計算了 Lennard-Jones 勢下的分子團簇最低能量。DMC 方法是上世紀70 年代文獻[53]首次提出的一種采用隨機行走(random walk)求解分子Schr?dinger 方程基態波函數的方法。DMC 利用了Schr?dinger 方程和擴散方程之間的同構性，模擬擴散過程推動波函數逐步向基態演化，從而實現對目標函數全局最優化解的搜索。文獻[54]對擴散蒙特卡羅方法進行了非常深入細致的介紹，文獻[55]針對量子退火的綜述是目前國內較為完整的。

1998 年文獻[56]提出可以采用位于橫向磁場中的Ising 模型實現量子退火過程的方案，并對此方案進行數值仿真，證明其比經典退火過程具有更好的收斂于基態的能力。在這一模型中，橫向磁場被作為與溫度相似的擾動能量，推動量子系統以絕熱過程的方式向基態演化。此工作的意義在于為量子退火計算機的研究提供了具體實現路徑。

Ising 模型是統計物理中的一種模型，它具有表述簡單、內涵豐富和應用廣泛的特點，甚至在社會科學中都得到了成功的應用。將Ising 模型作為實現量子退火算法的理論方案，這意味著只要能找到可以形成Ising 模型的實際物理系統，就能按照他們的方案實現量子退火計算機。

Ising 模型由具有向上和向下兩個方向的小磁針排列組合而成，向上取1，向下取?1：

在小磁針排列為 {si}時 系統的總能量為：

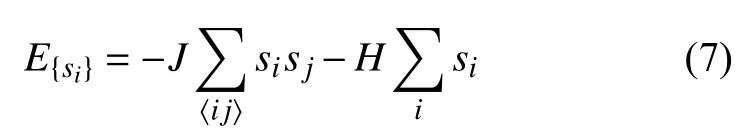
式中，J為能量耦合常數；〈ij〉代表對所有相鄰小磁針進行求和，如si=sj總能量減小J；H為外磁場強度，磁場向上為正，向下為負，如果小磁針方向也和外場一致，總能量減少一個單位。這表明在Ising 模型中所有磁針方向一致并與外磁場方向相同時能量最低。當外界溫度T越高時，就有數量越多的小磁針發生隨機翻轉。翻轉后小磁針的排列狀態為，如果此時能量則接受這次翻轉；如果此時能量，則以概率接受這一翻轉。在這一機制下系統會向能量較低方向演化，最終到達如下的能量分布狀態，即玻爾茲曼分布：

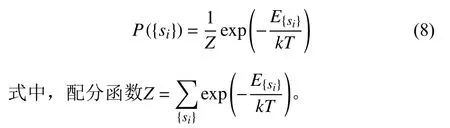
文獻[56]設計的量子退火方法采用橫向磁場Γ(t)作 為能量擾動，橫向磁場強度 Γ(t)隨時間逐步降低，推動系統達到基態。

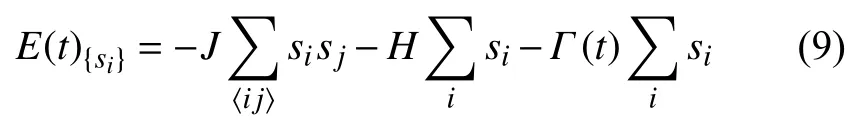
因此量子退火過程采用Schr?dinger 方程描述為：

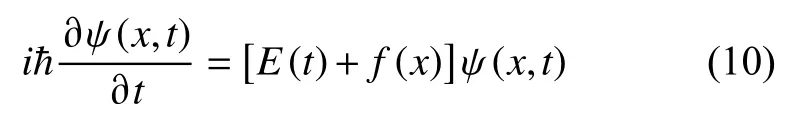
從智能優化算法的角度看這其實是表達一個多尺度的搜索過程，Γ (t)的值逐步減小時量子隧道效應逐步降低，搜索尺度減小。

1999 年文獻[57]在《Science》上報道他們成功地采用Ising 磁體材料在橫向磁場內實現了簡單的量子自旋模型。這一成果為采用量子退火計算機實現對優化問題的求解找到了一個具體實現方案，并首次從實驗上證明了量子退火在求解優化問題中的可行性。意大利高等國際研究院(International School for Advanced Studies,SISSA)的一個項目組也對量子退火在優化問題中的實現進行了大量的研究，證明了這一方法在實踐中的可行性[58-59]。

2011 年基于量子退火原理的D-Wave 量子計算機成為了世界上第一臺可以商用的量子退火計算機，D-Wave 同樣采用了橫向場Ising 模型，D-Wave中的量子比特不是用于量子門操作的，而是用于構造Ising 模型的[60]。D-Wave 主要的用途就是進行優化問題的求解，D-Wave 在求解優化問題時并不涉及具體的算法，而是通過退火過程由大自然給出問題的答案。

從隱含并行性的觀點來看，D-Wave 獲得快速求解優化問題的能力也是由于對于最終解的確定性的放松，其加速效果是針對強力搜索算法而言的。事實上大多數運行在經典計算機上的智能優化算法都能在較短的時間內獲得一個組合優化問題的可行解，其采用的方法也放松了對解正確性的嚴格要求。量子退火計算機和經典計算機上的智能優化算法獲得的快速計算能力都可以利用隱含并行性得到解釋，量子退火計算機并不一定會比經典計算機上的智能優化算法快，只是兩者運行的物理載體不一樣。

量子退火技術在解決優化問題的理論和實踐上的成功證明了優化問題具有量子可描述性，即可以采用一個量子模型對優化問題進行描述，同時智能優化算法的迭代演化過程也可以由一個量子系統的演化過程來描述。當按照量子退火算法中的勢能等效關系對智能優化算法進行建模后，可以發現智能優化算法的迭代采樣過程就是滿足Schr?dinger 方程所描述的演化過程的。

量子動力學在智能優化算法中的應用得益于量子科學領域中量子退火算法的出現。智能優化算法的研究人員在廣泛借鑒量子比特這一概念時，對物理學中的量子退火方法有所忽略，而正是量子退火算法才真正的指出了智能優化算法與量子理論之間密切的聯系，而不僅僅是概念的借鑒。

將量子力學引入智能優化算法更為重要的目的是希望能采用量子力學的數學框架分解出智能優化算法迭代過程的基本操作。智能優化算法的迭代過程是一個時間演化過程，因此描述智能優化算法的數學工具應該是一種動力學方程。量子退火思想的引入為建立智能優化算法的量子模型提供了契機，量子退火在處理優化問題時具有獨特的優勢。

量子退火的核心思想有4 點：

1) 將優化問題的目標函數視為量子系統中的粒子勢能；

2) 量子系統能量最低的基態就是優化問題的解；

3) 通過逐步降低外在能量擾動使量子系統能量逐步演化到基態；

4) 優化問題的解采用概率化的波函數進行表達。

6 量子動力學理論

量子退火的思想為建立智能優化算法的量子模型提供了思路，智能優化算法有可能自身就是一個可以被量子力學所描述的過程，即可以用Schr?dinger方程來完整地描述智能優化算法的時間演化過程。與量子退火理論相似，如果將優化問題的目標函數f(x)作 為量子系統中粒子的約束勢能V(x)，即V(x)=f(x)，就可以得到如下的智能優化算法的Schr?dinger方程：

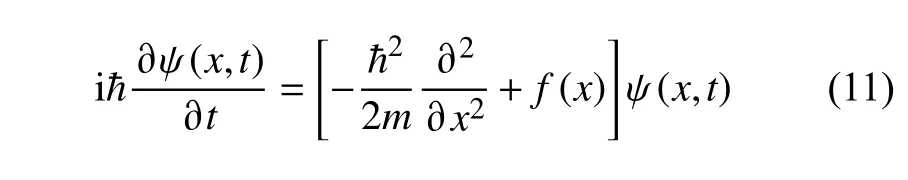
這一思想在文獻[21-22]提出的量子粒子群算法中得到了部分的采用。QPSO 算法的經典版本采用 δ勢阱對應的基態波函數來構造采樣函數，受粒子群算法的影響并未明確指出V(x)=f(x)的關系，算法的整體構造思路不是徹底量子化的，算法的核心迭代結構還是以粒子群算法為基礎。QPSO 算法在性能上獲得了成功，但在高維函數優化時容易陷入局部最優。QPSO 將采樣函數與波函數對應起來的想法具有了智能優化算法量子模型的雛形。這使智能優化算法向量子理論邁進了一步，但其并未建立起智能優化算法和量子力學之間的數學物理關系，也沒有意識到目標函數與勢能之間的關系，這使得QPSO 算法不能真正的成為量子化的算法，更未能為智能優化算法建立量子模型。

明確將智能優化算法的目標函數視為Schr?dinger 方程中勢能的算法是多尺度量子諧振子算法(MQHOA)[61-64]。MQHOA 算法依據量子諧振子的波函數構造了智能優化算法，這一提法使智能優化算法向量子模型前進了一步。在該算法中還定義了波函數、零點能等量子物理中的重要概念[65]，并對多尺度過程和不確定性關系進行了研究[66]。但有意思的是從量子動力學的角度看MQHOA 算法的模型并不是完全正確的，在模型的應用上顯得牽強。然而其構造出的算法結構卻就是智能優化算法量子動力學所指出的基本迭代操作，而且MQHOA算法及其改進算法的性能也得到了一定程度的驗證[67-72]。這些結果“意外”地證明了智能優化算法量子動力學給出的基本操作是簡單而有效的，可以作為構造性能更好的算法的基礎。MQHOA 算法利用了智能優化算法的Schr?dinger 方程[73]，但卻未能明確指出并利用Schr?dinger 方程作為動力學方程來研究智能優化算法。雖然其在算法結構上基本與動力學模型給出的操作相似，但物理解釋卻不正確。MQHOA 算法和QPSO 算法都可以認為是量子動力學模型的萌芽。

為解決該問題，文獻[74]對智能優化算法的量子基礎進行了討論，確立了勢能等效、優化問題的含時Schr?dinger 方程等一系列從量子視角研究智能優化算法的理論基礎。為了利用經典計算機模擬智能優化算法在搜索過程中的隨機馬爾可夫過程，對Schr?dinger 方程做Wick轉動[75]，將時間轉變為虛時間并令，則智能優化算法的含時Schr?dinger 方程重新寫為：

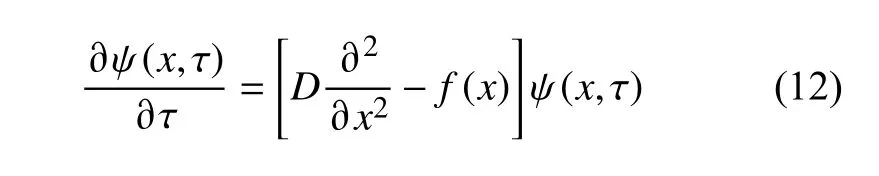
智能優化算法的含時Schr?dinger 方程就是智能優化算法的量子動力學方程，它從量子力學的角度描述了智能優化算法的時間演化過程，智能優化算法的迭代演化過程通過Schr?dinger 方程轉化為波函數 ψ (x,τ)的時間演化過程。Schr?dinger 方程所對應的基態波函數就是優化問題所對應的解。從理論上講，在f(x)已知的情況下可以通過求解Schr?dinger方程獲得基態波函數。

該文采用擴散蒙特卡羅方法來求解基態波函數。雖然擴散方程和Schr?dinger 方程在形式上是相似的，但優化問題約束條件f(x)的引入卻破壞了式(12)格林函數的歸一性，其格林函數為：

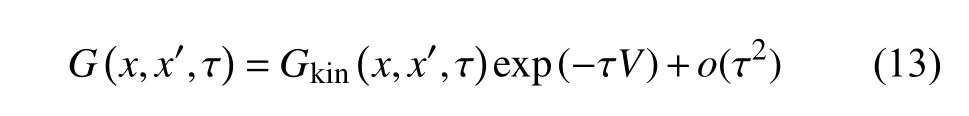
式中，勢能項因子 exp(?τV)破壞了上式的歸一性，因此需要向上述格林函數中引入一個收斂因子exp(τER)，使式(12)所描述的系統得到穩定收斂的解，改變后的格林函數是調整后的Schr?dinger方程的解，其公式如下：

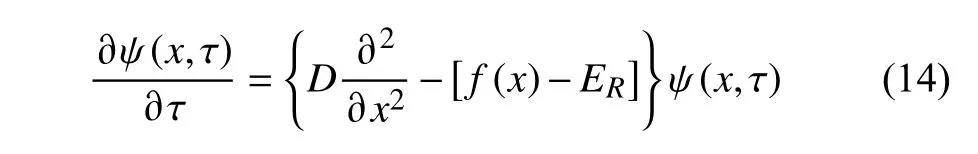
式中，ER是參考能量，是對當前優化系統能量的估計值；f(x)?ER是系統的勢能項，反應優化問題對優化系統的影響。隨著優化系統的演化，粒子的分布將不斷的變化從而使參考能量ER不斷逼近基態能量。式(14)即為一般意義上優化問題的含時Schr?dinger 方程。

建立智能優化算法的Schr?dinger 方程具有兩個重要的理論意義：

1) 從物理意義上，優化問題通過Schr?dinger方程被轉化為求解受勢能f(x)約束的量子系統的基態波函數ψ0(x)；

2) 從數學意義上，將優化問題和優化系統納入統一的方程描述，即Schr?dinger 方程這個線性偏微分動力學方程。這意味著量子力學中求解該方程的過程可以用作解釋量子動力學理論下的智能優化算法的優化過程。

通過Schr?dinger 方程，智能優化算法在量子視角下被轉換為一個模擬的物理優化系統，該系統由量子空間中的虛擬粒子組成，優化問題的目標函數轉換為加之于該系統的約束勢場，而該系統的運行方式符合Schr?dinger 方程的描述。

對于智能優化算法的Schr?dinger 方程，可以通過Feynman 積分的方法，利用初態 ψ(x0,0)在A至B 所有路徑上的積分，描述粒子從A 到B 的狀態變化。Schr?dinger 方程任意位置x和 時間 τ的解ψ(x,τ)可以表達如下：

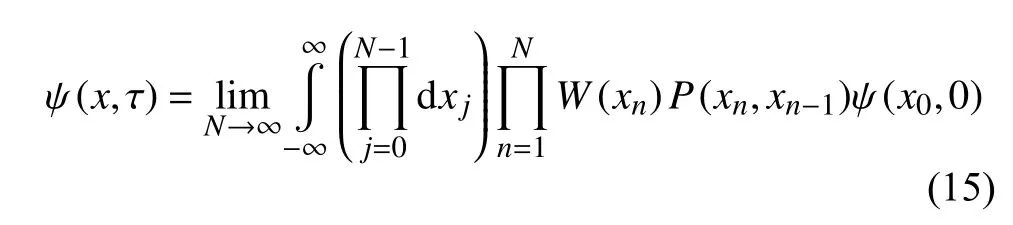
式中，P(xn,xn?1)為虛擬粒子隨機運動的動能相關項，描述了粒子的運動行為，與當前粒子位置xn?1和 粒子的質量m有關，其公式如下：

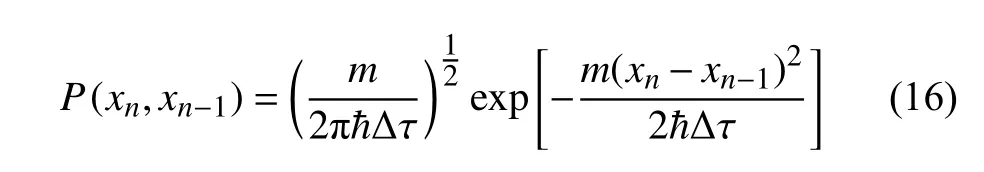
式(15)中，W(xn)為概率權重項，描述了粒子通過隨機運動出現在xn的幾率，與當前采樣結果f(x)和 參考能量ER有關，其公式如下：

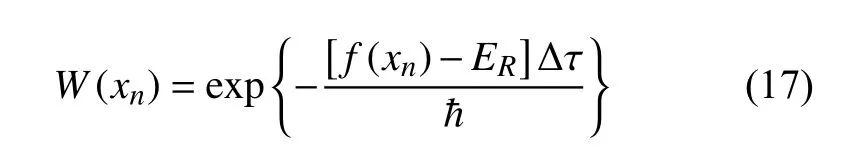
式(15)以積分的形式描述了在擴散過程中自由粒子運動和密度的變化，由于標準數值積分方法難以求解該積分，因此采用了擴散蒙特卡羅方法。在擴散蒙特卡羅方法中，如果函數h(x)可以分解為函數f(x)和 概率函數p(x)的乘積，則該積分可以表示為f(x)在 密度p(x)下的期望，其公式如下：

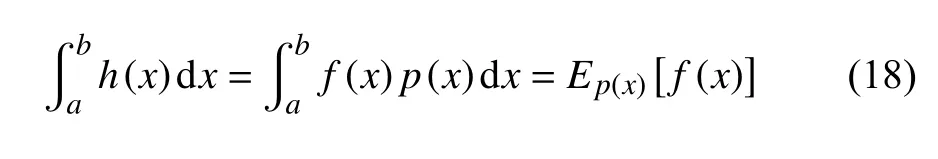
根據式(15)，采樣密度函數為：

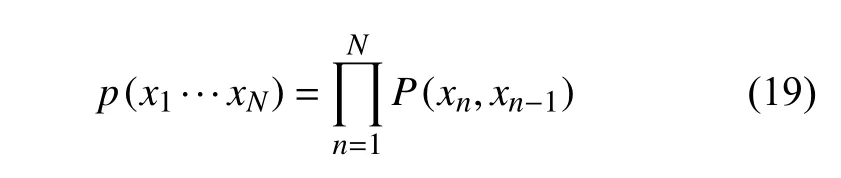
狀態函數f(x1···xN)為：

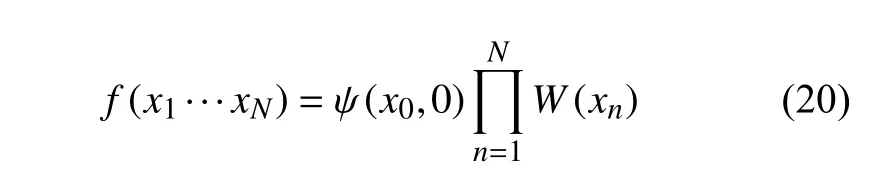
因此，式(15)可以通過p(x1,···,xN)密度下的采樣和權重函數W(xn)對采樣結果的調整來獲取：

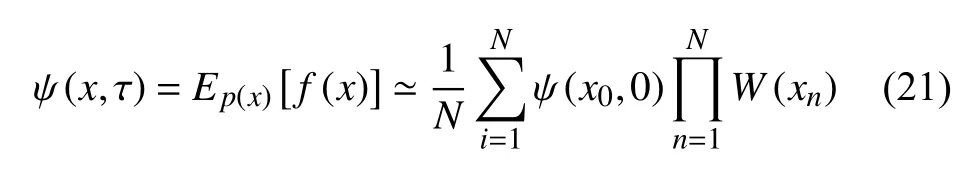
由“擴散采樣?權重調整”組成的迭代循環即為量子力學中求解Schr?dinger 方程常用的擴散蒙特卡羅方法，其模擬了粒子在Schr?dinger 方程下通過隨機運動向基態能量演化的過程。

同時，多尺度退火過程是通過逐步降低模擬量子優化系統的動能實現的，公式如下：

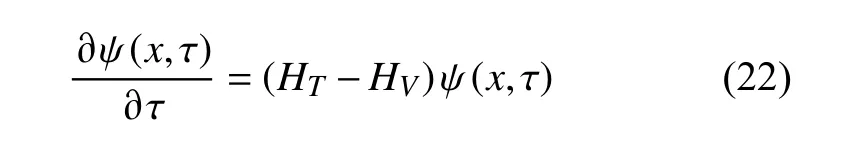
式(22)中HT與粒子擴散公式(16)中的搜索尺度是正相關的。其原因是因為在優化過程中，目標函數的規模與模擬量子優化系統的規模不總是一致的，因此需要不斷的改變優化系統的搜索尺度HT以匹配動能HV，這也是量子退火中減少能量擾動的原因。

智能優化算法量子動力學下的基本對應關系和操作匯總如表1。

表1 智能優化算法量子動力學下的基本對應關系和操作

特別有意思的是量子動力學模型并非想象中的那樣給出一個量子化的新智能優化算法，而是得到了一些操作和基本迭代方法。其核心操作主要包括：正態采樣、權重計算、多尺度過程，其他很多智能優化算法都可以視為在這一核心操作的基礎上進行改進。智能優化算法的量子動力學解釋了智能優化算法的量子化本質，為利用量子力學對智能優化算法進行分析提供了基礎。

7 智能優化算法的核心操作

從量子動力學可以得到一些Schr?dinger 方程下的智能優化算法的基本操作，這一結果提示：一些基于不同算法模型的智能優化算法都是從這些基本操作過程中衍生出來的。這一問題似乎也被不少研究者所注意到了，雖然他們可能并未從量子力學的視角去解釋，但卻發現智能優化算法可能存在“骨架”結構。

7.1 Kennedy 對粒子群算法基本框架的探索

粒子群算法(particle swarm optimization,PSO)是Kennedy 和Eberhart 在1995 年提出的一種群體智能優化算法[76]。Kennedy 認為這一算法的迭代過程模擬了鳥群的社會行為，這一算法的核心思想是通過個體行為和社會行為的綜合來決定每一個體下一步的行為。

在PSO 算法中每次迭代都要保存個體的最好位置 pbest 和群體中的最好位置 gbest，每一個粒子的位置更新公式如下：

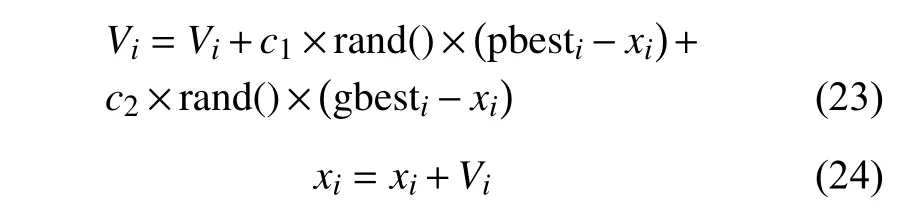
式中，學習因子c1和c2需 要人為確定，c1=0時粒子運動不考慮自己的個體歷史信息，c2=0時粒子運動不考慮群體的歷史信息。其參數值的設定帶有很強的主觀色彩，什么時候要考慮、考慮多少都是人為定的，這給算法性能優化造成很大的困難。同時由于這一算法最初沒有采樣尺度的遞減策略，其性能并不是太好。直到1998 年文獻[77]在PSO 算法的速度公式中引入遞減的慣性權重因子w，才使PSO 算法成為一個多尺度算法，新的速度計算公式如下：

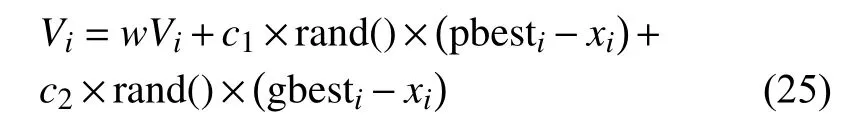
在迭代過程中通過逐步減小w的值，實現全局搜索和局部搜索的平衡。后來Clerc 又增加了控制速度的約束因子α，約束因子成為了一個不折不扣的多尺度參數[78]，也使PSO 算法成為一個多尺度搜索算法。

多尺度策略是智能優化算法量子模型中不確定性原理所預言的一種基本迭代操作[65]。如同量子理論中位置和動量不能同時被測定[64]一樣，智能優化算法在同一尺度下不能同時實現良好的全局搜索和局部搜索能力。加入慣性權重后，PSO 算法成為一種多尺度群體算法。慣性權重的引入在算法上是正確的，但在模型上卻顯得牽強，這使得PSO 算法逐步離開了Kennedy 他們所提出的基本模型。特別是后來大量的改進算法和混合算法更是走得越來越遠，PSO 也就逐漸成了一個算法名稱的符號。

在PSO 算法提出近十年時，也就是2003 年左右，Kennedy 也意識到PSO 算法的參數變化太多而使算法難以理解，因此想簡化PSO 算法。并且他認為PSO 算法與其他算法存在相似性，這一點與采用從量子動力學中得到智能優化算法的基本迭代操作是相似的。因此他提出了PSO 算法的骨架(bare bone)算法[79]，在這篇文章中Kennedy 采用隨機正態采樣取代了速度，取得了更好的性能。他認為正態采樣既有很好的鄰域采樣能力，又能以較小的概率采到距離當前位置較遠的位置。Kennedy在文中也自嘲道：“這樣鳥在空間里的‘飛行’就變為‘飛濺’了。”同時他還認為PSO 算法和其他的一些進化算法有可能應該被歸類到一個統一的優化種類中去。雖然他并未明確地給出統一模型，只是進行粗略的描述，但這一認識可能是對智能優化算法進行統一建模思想的雛形。Kennedy 所得到的一些結論與采用量子動力力學作為統一模型所得到的結論幾乎完全吻合。就在PSO 算法的骨架提出的第二年即2004 年的CEC 會議上，Kennedy明確放棄了從鳥群模型構造的速度項，提出了一種基于正態隨機采樣的更為簡潔的算法[80]，其采樣公式如下：

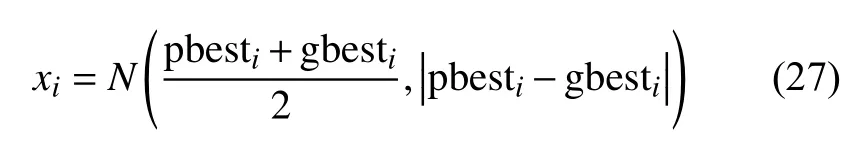
對于其在算法中采用的正態隨機采樣在量子動力學中也曾早有預言。在擴散蒙特卡羅方法中，量子動力學方程轉化為擴散方程，而擴散方程的格林函數就是正態函數，它代表了擴散過程中粒子在下一時刻到達某一位置的概率，其含義就是隨機采樣時的采樣概率函數，從量子力學來看也就是波函數，即粒子出現在某一位置的概率。

至此Kennedy 將PSO 算法的演化過程簡化為簡單的正態概率采樣過程，其基本結構與量子動力學給出的智能優化算法基本迭代結構已較為接近，但量子動力學給出的迭代過程則更為簡單清晰。

7.2 智能優化算法的基本迭代過程

當從智能優化算法的量子動力學的角度去解釋智能優化算法的迭代過程時，智能優化算法的核心迭代操作就成為了量子動力學理論框架下的基本要求。有的學者誤認為近年提出的“黑洞算法”其結構來源于粒子群算法[82]，也有學者將MQHOA 算法誤認為是一種量子粒子群算法，產生這些誤解的原因皆源自智能優化算法可能具有統一的內在核心操作。差分進化算法[83-84]和煙火算法[85]的研究者也紛紛提出自己的“骨架”算法，這些骨架算法都存在相似的基本操作，如概率采樣過程、采樣步長的變化和群體策略等。通常這些看上去簡單的骨架算法都具有不錯的優化性能。這更是進一步證明了智能優化算法的核心操作是一種非常有效的操作，它已能滿足智能優化算法對性能的基本要求。

綜合量子動力學智能優化算法和其他智能優化算法的“骨架”，可以給出一個較為通用的迭代過程如下。

以上基本迭代過程看上去非常簡單，仿佛也沒有任何量子力學的痕跡，但卻可以由智能優化算法的量子動力學通過擴散蒙特卡羅分解出來。而如果將正態采樣視為格林函數，則其量子的面紗就揭開了。類似的，在QPSO 算法中也將其使用的拉普拉斯采樣函數視為勢阱下的基態波函數[86]。

智能優化算法的基本迭代過程可以作為智能優化算法設計和改進的基礎，量子動力學可作為算法分析的理論框架，同時實驗結果表明，上述基本迭代操作的骨架算法已出人意料地具有了相當的優化性能。而大量增加了許多操作機制的“重型”智能優化算法卻仿佛只是為了走好最后一公里的性能而給出的，這使我們猜想：當目標函數為黑盒且沒有針對目標函數做任何先驗估計和假設的情況下，骨架算法可能已是“最優”算法了。

8 結束語

從量子視角來認識和研究智能優化算法是一個非常有前景的研究方向，從量子比特概念引入智能優化算法到直接采用量子動力學模型來為智能優化算法建模，該領域的研究正在走向縱深。通過量子視角來研究智能優化算法有望解釋智能產生的原因并為研究隱含并行性產生的機制提供一條可行的道路。在當前量子科技成為我國戰略性新興技術的歷史機遇下，基于量子技術的智能優化算法研究一定會取得長足的發展。