大視場室內移動機器人高精度動態定位方法
田明銳 楊 皓 胡永彪
1.長安大學道路施工技術與裝備教育部重點實驗室,西安,7100642.廣西柳工機械股份有限公司,柳州,545006
0 引言
室內移動機器人是運行在室內環境的自主移動機器人,如工業生產機器人、服務機器人、醫療機器人和倉儲機器人等[1-3]。目前,關于室內移動機器人領域的研究主要集中在室內定位、自主導航、運動控制和協同作業幾個方面,其中室內定位技術是移動機器人完成其他任務的基礎與前提。相對于室外定位技術大都依賴衛星定位的情況,室內定位技術受到室內環境復雜性和動態性的影響,一直是機器人定位技術研究領域的難點與熱點。
借助于不同的傳感器技術,室內定位方法種類繁多,包括紅外定位[4]、超聲波定位[5]、無線網絡定位[6]、藍牙定位[7]、激光雷達定位[8]和視覺定位[9]等。機器視覺傳感器對復雜環境的強感知性和圖像處理技術獲得的高精度定位使視覺定位方法受到了廣泛的關注[10]。
目前,基于視覺的室內定位方法主要分為相對定位方法和絕對定位方法兩類。
相對定位方法利用固定在移動機器人上的相機傳感器采集周圍環境圖像并處理,通過檢測環境中的人工標識來進行機器人的定位。謝家浩等[11]研究了一種基于視覺同步定位與建圖(SLAM)的相對定位方法,采用ORB(oriented FAST and rotated BRIEF)算法對特征點進行提取和描述,實現了對目標物的實時定位。楊鹿情[12]設計了一種將顏色特征與形狀特征相結合的人工信標,利用串聯式組合誤匹配剔除算法實現室內移動機器人的定位,減小了單目視覺SLAM系統前端存在的較多誤匹配對位姿估計的影響。相對定位方法定位迅速,精度較高,但需安裝大量機載設備,成本較高,同時該方法算法復雜,易受環境不確定因素的影響。
相比之下,絕對定位方法通過置于環境中的相機傳感器對目標物及周圍環境進行圖像采集,通過圖像處理進行移動機器人的定位,可有效降低機器人機載設備的復雜性,同時具有成本低、適應性強和算法簡單等優點。黎安慶等[13]提出了一種基于分布式視覺技術的機器人絕對定位方法,在3 m×5 m的區域內該方法的平均定位精度為8.1 cm,方位角平均精度為8.05°。林劍冰等[14]采用定距雙球作為標志物,設計了一種室內自動運輸車的絕對定位系統,可同時實現其位置與方向的定位,相對誤差一般情況下保持在1.5%以內,在距離系統3 m范圍的短距離定位的絕對誤差小于1 cm。李鵬等[15]提出了一種基于標定板絕對定位方案,利用高斯混合模型背景減除法檢測機器人運動區域,縮小了標定板角點的提取范圍,提高了定位的實時性,當機器人速度為0.3 m/s時,平均定位精度為6.86 cm。
上述絕對定位方法研究為保證定位精度,視場范圍設置相對較小,在機器人低速移動時可滿足較高的實時定位要求。目前,關于大視場范圍與高速移動目標的絕對定位方法研究較少。本文對大視場范圍移動機器人的高速動態定位方法進行了研究,將相機多參量非線性標定方法與基于光信標高速定位算法相結合,提高高速移動機器人的定位精度。
1 基于多相機的大視場傳感器系統
1.1 定位系統硬件配置與軟件構架
如圖1所示,定位系統硬件由一組具有外部同步觸發器的相機、一臺工控機和LED光信標組成,定位面積即相機總視場可達43 m2。系統選用MER-131-75GX-P工業相機進行圖像采集,相機內部采用CMOS感光芯片,采集圖像分辨率為1280×1024。每臺相機通過GigE數據傳輸線連接到處理節點,允許以每秒75幀的速度進行圖像采集。處理節點為一個通用的多核PC平臺,具有控制和處理來自多個相機信息的能力。實驗中使用的所有機器人平臺采用Traxxas-83024-4輪式機器人底盤,采用全輪驅動、前輪轉向的方式運動,最高速度可達48.3 km/h。機器人上部安裝220×20 mm的LED光信標,其方向與機器人幾何中心線平行,光信標的幾何中心與機器人的質心重合。
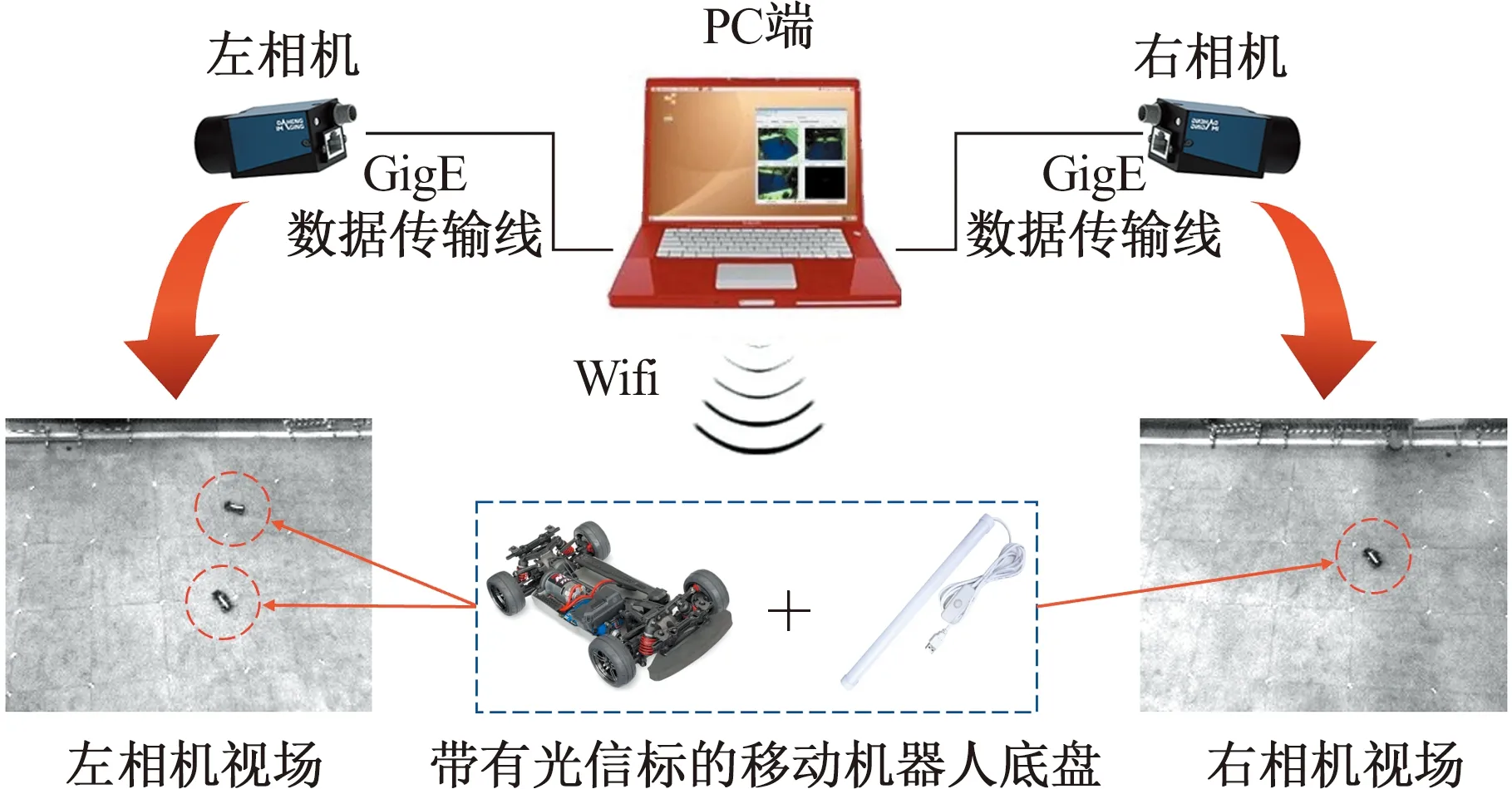
圖1 定位系統方案示意圖Fig.1 Schematic diagram of positioning system hardware
定位系統軟件使用C/C++語言實現程序框架和定位功能算法,利用MATLAB相機標定工具完成視覺系統標定,其構架如圖2所示。該軟件系統主要由相機標定、移動機器人定位、動態誤差補償三方面構成。
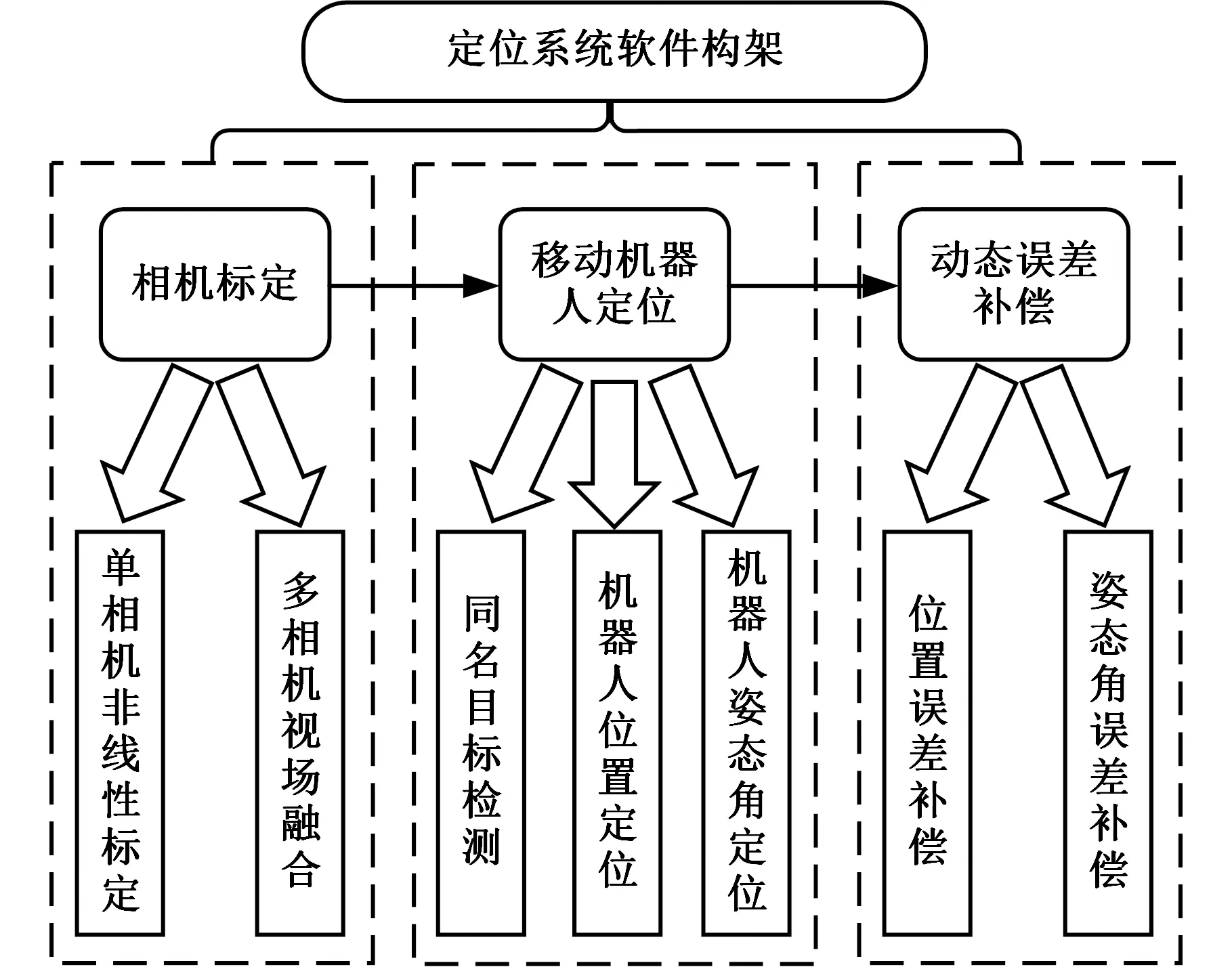
圖2 定位系統軟件構架Fig.2 Positioning system software architecture
1.2 大視場多相機非線性標定
1.2.1多參量非線性標定方法
相機標定旨在獲得圖像坐標(u,v)與地面坐標(xw,yw)的映射關系,是后續定位系統實現的前提。傳統相機的線性標定方法不考慮圖像的徑向、切向的畸變,標定后的精度較低,且對噪聲敏感。相機的非線性標定方法引入了相機的畸變參數,成像模型更加精確,可有效提高標定精度。
傳統的相機非線性標定[16]借助一組靶標數據對相機參數進行標定,當視場范圍增大時,該標定方法精度較低。為提高大視場環境下的相機標定精度,排除偶然誤差的影響,本文選用多組靶標對相機進行非線性標定,靶標組數的選取與相機視場大小相關。
第k(k=1,2,…,n)組靶標中第i個靶標點的圖像坐標與地面坐標滿足如下關系:
(1)
式中,m′k11、m′k12、m′k14、m′k21、m′k22、m′k24、m′k31、m′k32為標定參量。
式(1)的矩陣方程形式為
Akm′k=Bk
(2)
Ak=
m′k=
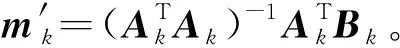
利用k個單應矩陣計算平均單應矩陣:
(3)
將該平均單應矩陣作為最終將圖像坐標映射至地面坐標的單應矩陣。
根據式(1)和式(3)可計算相機圖像坐標(ui,vi)映射至地面的坐標(x′wi,y′wi)。相機的標定誤差即定位系統的靜態誤差在地面坐標系xw、yw方向上分別為Ex=|xwi-x′wi|、Ey=|ywi-y′wi|。該標定方法和僅選用一組靶標點的標定方法相比可有效提高定位精度。
非線性標定實驗利用MATLAB中的Camera Calibrator相機標定工具,對相機內部參數進行標定,結果如表1所示。
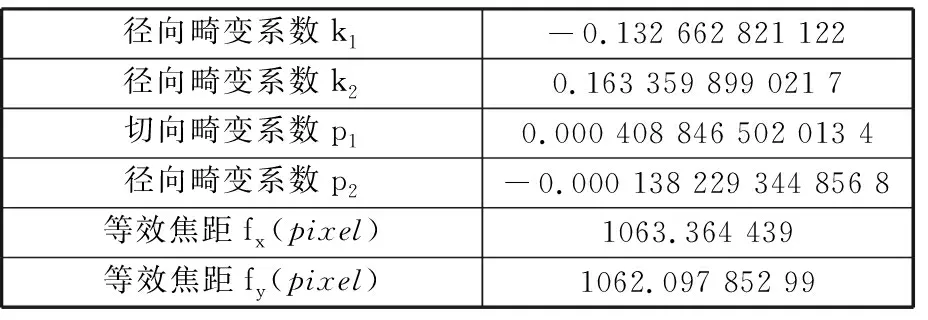
表1 相機內部參數
根據相機內參數據,對相機所采集的圖像進行去畸變校正。由于單個相機視場約為25 m2,故在去畸變后的圖像中共選取4組靶標點作為單應矩陣的標定點,即k=4。根據式(1)~式(3)計算左右兩相機的平均單應矩陣:
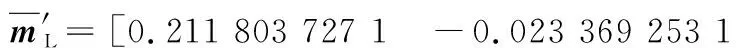
(4)
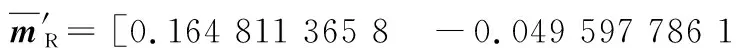
(5)
根據式(1)、式(4)、式(5)計算地面所有靶標點的世界坐標,并利用MATLAB中Curve Fitting工具擬合出所有像素點靜態誤差,如圖3所示,定位系統的平均靜態定位精度為2.26 mm。若只選取單組靶標點,即k=1,則經計算得定位系統的平均靜態定位精度為4.77 mm。基于多組靶標點的相機非線性標定方法使相機標定精度提高約52.6%。
1.2.2多相機視場融合
在大視場移動機器人定位之前,需將各相機成像平面坐標統一化,即多相機視場融合,作為后續同名目標檢測的計算基礎。同一平面目標點在不同成像平面上的映射關系可通過單應矩陣變換表達,因此本文基于不同視場圖像坐標系的單應矩陣標定來實現多相機視場融合。
選取同時出現在相機p、相機q視場中的4個靶標點,組成兩組圖像坐標(upi,vpi)、(uqi,vqi),i=1,2,3,4,代入下式:
(6)
根據1.2.1節所述方法,計算相機q映射至相機p的單應矩陣m′q-p,可得由右相機標定至左相機的單應矩陣:

(a)左相機Ex
(7)
2 動態定位系統算法設計
2.1 基于光信標的高速目標定位算法
模板匹配、光流法和幀差法等算法是基于圖像的運動目標檢測及定位的常用方法。模板匹配法能夠適應較為復雜的背景,定位精度較高;光流法與幀差法可直接獲得目標物的運動信息,易于進行實時處理。當定位目標增多,且目標物高速運動時,上述定位算法會非常復雜,圖像處理時間長,造成定位系統實時性較差、動態定位誤差大等問題。為解決高速多目標定位算法的上述問題,本文提出基于光信標的高速定位算法。該算法定位目標具有較高的移動速度,并涉及跨視場多目標的定位問題,算法流程圖見圖4。
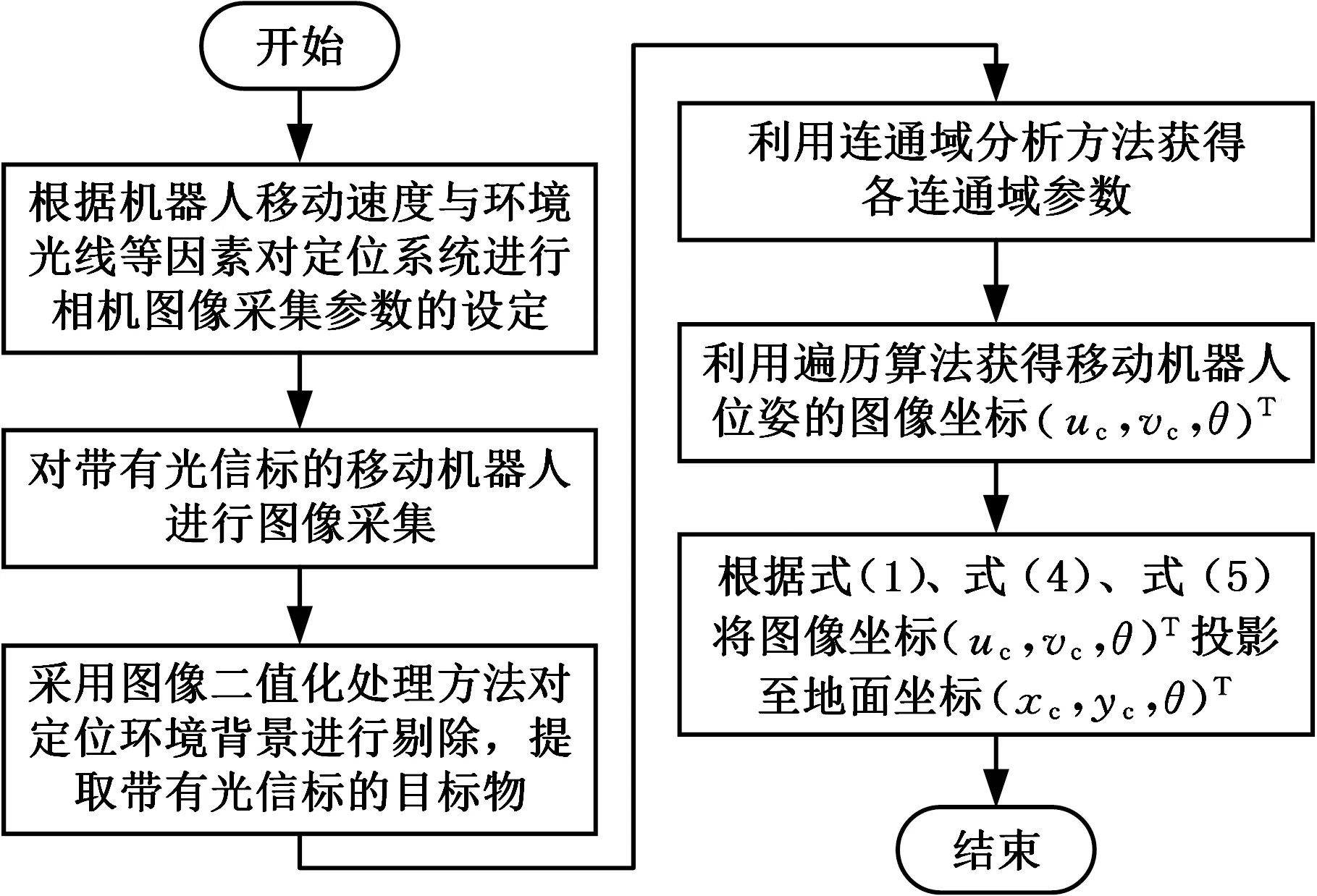
圖4 基于光信標的高速定位算法流程圖Fig.4 Flow chart of high-speed positioning algorithmbased on optical beacon
使用光信標能夠簡化圖像運動目標檢測算法,有利于提高定位算法的運行速度。該定位算法設置較短的相機曝光時間,借助固定閾值方法快速提取圖像中安裝光信標的移動檢測物體,得到無其他干擾的目標物二值圖像。設原圖像像素點灰度級為f(u,v),二值化后圖像像素點灰度級為g(u,v),固定閾值為T0,則二值化計算公式為
(8)
針對二值化處理后的圖像,利用連通域分析與循環遍歷算法,獲得連通域外接矩形的長h、寬w、質心坐標(uc,vc)和左上角點坐標(u0,v0)等參數。由于光信標的中心與機器人質心重合,連通域外接矩形的圖像質心坐標(uc,vc)為機器人質心的圖像坐標,故可根據式(1)、式(4)和式(5)計算機器人質心的位置坐標(xc,yc)。
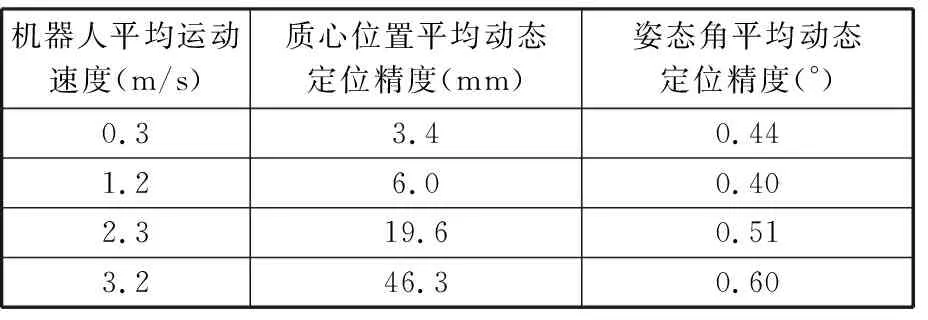
移動機器人的姿態角計算示意圖見圖5。首先,根據外接矩形長寬比的不同(圖5a為w>h,圖5b為w (9) (a)w>h(b)h>w圖5 機器人姿態角計算示意圖Fig.5 Schematic diagram of robot attitudeangle calculation 式中,ucl、uc(l-1)分別為第l與第l-1時刻機器人質心的圖像橫坐標值。 移動機器人的位姿信息包含其質心坐標與姿態角,向量形式表示為(xc,yc,θ)T。 考慮相機布置中存在一定的視場重合區域,當物體位于重合區域時將同時出現在兩個相機的圖像中,如何區分不同視場中的同名目標物是多相機定位方法中的一個關鍵。在目標定位計算前,可對相鄰相機視場圖像中的同名目標物進行判別與剔除,避免同名目標的重復定位計算。 跨視場同名目標檢測算法將同一時刻相鄰相機采集的圖像進行處理,分別獲得左相機、右相機圖像中所有連通域目標的質心參數(uLcj,vLcj)和(uRci,vRci),結合1.2.2節中得到的單應矩陣,將右相機圖像中所有質心點(uRci,vRci)映射至左相機圖像中,得到(u′Rci、v′Rci)。計算映射后各質心點坐標(u′Rci、v′Rci)與左相機圖像中原質心點坐標(uLcj,vLcj)間的距離: (10) 將其與距離閾值Te比較,進而判定右相機中對應目標物是否為同名目標物,并將其排除,Te的選取與相機參數、相機的布置以及移動機器人幾何尺寸參數有關,可通過實驗方法確定。設命題Q(i)為右相機中第i個目標物為同名目標物,當Q(i)=TRUE時該目標為同名目標物,當Q(i)=FALSE時該目標為非同名目標物,其判別公式如下: (11) 該算法通過比對左右相機中每個連通域目標質心坐標,利用式(11)實現同名目標的判別和剔除,其流程如圖6所示。 圖6 同名目標檢測算法流程圖Fig.6 Flow chart of same-named targetdetection algorithm 盡管上述高速定位算法程序運行周期較短,但系統仍會產生一定的時延,尤其目標物處于高速移動時,系統輸出的位姿信息滯后較為嚴重,即定位系統存在一定的動態誤差,因此,需進行動態定位誤差的補償以提高系統定位精度。 由于程序運行周期較短,故假設機器人行駛速度v在同一運行周期內保持不變。選取機器人質心(x,y)為第一特征點,建立該特征點的運動學方程[17]: (12) (13) 式中,下標m表示時刻;T為程序運行周期;vx、vy為第一特征點在圖像空間中x、y方向上的速度。 同理,選取機器人姿態角θ為第二特征點,建立該特征點的運動學方程: θm+1=θm+vθT (14) vθ=(θm-θm-1)/T (15) 式中,vθ為第二特征點的變化率,即角速度。 動態定位誤差補償算法基于上述運動學模型,在C/C++語言編程環境中開發,分析計算機器人的移動軌跡、速度和方向等信息,預測定位系統存在時延時機器人的真實位姿,完成誤差補償。該算法流程圖見圖7。 圖7 動態定位誤差補償算法流程圖Fig.7 Flow chart of dynamic positioning errorcompensation algorithm 根據2.1節提出的定位算法,以左相機為例,設置合適的曝光參數,使圖像能夠清晰完整地顯示移動機器人上安裝的光信標,程序運行結果如圖8所示。由輸出結果可知,共檢測到三臺移動機器人,分別為Car_0、Car_1和Car_2,它們對應的位姿向量分別為(579.28 mm,385.67 mm,36.87°)T、(583.28 mm,482.33 mm,-36.87°)、(692.84 mm,569.38 mm,124.13°)T。 圖8 移動機器人位姿計算程序運行結果Fig.8 Running results of mobile robot position andattitude angle calculation program 首先進行距離閾值Te的設定。選取三組位于相機視場重疊區域的地面坐標點(xLcj,yLcj)、(xRci,yRci),i,j=1,2,3(即每組包含3對坐標點),分別獲得它們位于左圖、右圖中的圖像坐標(uLcj,vLcj)、(uRci,vRci)。同時根據1.2.2得到的單應矩陣m′R-L,將位于右圖中的三組坐標點映射至左圖并統計映射誤差eui=|u′Rci-uLcj|、evi=|v′Rci-vLcj|,結果如表2所示。 表2 坐標點映射誤差 根據表2中數據,結合移動機器人幾何尺寸,將距離閾值Te設定為25 pixel。而后,根據2.2節中算法,對視場范圍中圖9所示的移動機器人分布進行同名目標的檢測與排除,該視場范圍內共有四臺移動機器人,其中2號、3號為出現在視場重疊區域的同一移動機器人。 圖9 兩視場中移動機器人分布Fig.9 Distribution of mobile robots in twofields of view 該算法的輸出結果如圖10所示,成功檢測出3號機器人為同名目標物并對其進行了剔除,最終獲得三個有效目標,分別用Car_0、Car_1與Car_2表示。由結果可知,該算法能夠準確地判斷有效目標并去除重復同名目標,為定位系統檢測多目標的準確性提供保障。 圖10 同名目標檢測程序運行結果Fig.10 Running results of same-named targetdetection algorithm 在獲得移動機器人靜態位姿且進行了同名目標檢測與排除的前提下,通過實驗驗證機器人在0.3 m/s、1.2 m/s、2.3 m/s、3.2 m/s四組不同平均速度下動態誤差補償算法的有效性。當機器人處于最高平均速度3.2m/s時,其質心坐標實際值與估計值對比圖、姿態角實際值與估計值對比圖見圖11和圖12。 圖11 平均速度值為3.2 m/s時機器人質心軌跡實際值與估計值對比Fig.11 Comparison of the actual and estimated valuesof the robot’s center of mass position with the averagespeed is 3.2 m/s 圖12 平均速度值為3.2 m/s時機器人姿態角實際值與估計值對比Fig.12 Comparison of the actual and estimated valuesof the robot’s attitude angle with the averagespeed is 3.2 m/s 根據不同速度下的實際值與估計值對比圖得質心坐標誤差補償平均精度與姿態角誤差補償平均精度,如表3所示。 表3 動態誤差補償后定位系統精度 由表3可得,在移動機器人最高平均速度可達3.2 m/s時,系統位置平均動態定位精度為5 cm、姿態角平均動態定位精度為0.6°。 本文針對室內高速移動機器人實時定位問題,提出了一種基于視覺的高精度絕對定位方法。該方法利用多相機視場融合,實現了43 m2的大視場絕對定位,結合同名目標物排除算法,解決了多相機視場重疊區域機器人定位問題;利用多參量非線性標定方法,提高平均靜態定位精度至2.26 mm;采用光信標簡化圖像處理算法提高定位系統運行速度,并借助線性誤差補償算法,使機器人在平均速度為3.2 m/s時,定位系統位置平均動態定位精度達5 cm,姿態角平均動態定位精度達0.6°。實驗結果證明,該定位系統可實現室內大范圍下高速移動機器人的實時定位,定位系統的靜態與動態定位精度滿足要求。本文方法的局限性主要在于,大視場平面靶標點布置過程導致單應矩陣標定工作量較大,例如當移動機器人光信標到地面的垂直距離發生變化時,需要重新標定與地面平行的另一平面的單應矩陣,此時需要在目標平面內布置(x,y)坐標已知的若干靶標點,當精度要求較高時,靶標點布置難度和工作量較大。這也限定了各移動機器人光信標到地面的垂直距離最好相等。因此,后續工作還需研究大視場平面的快速標定方法。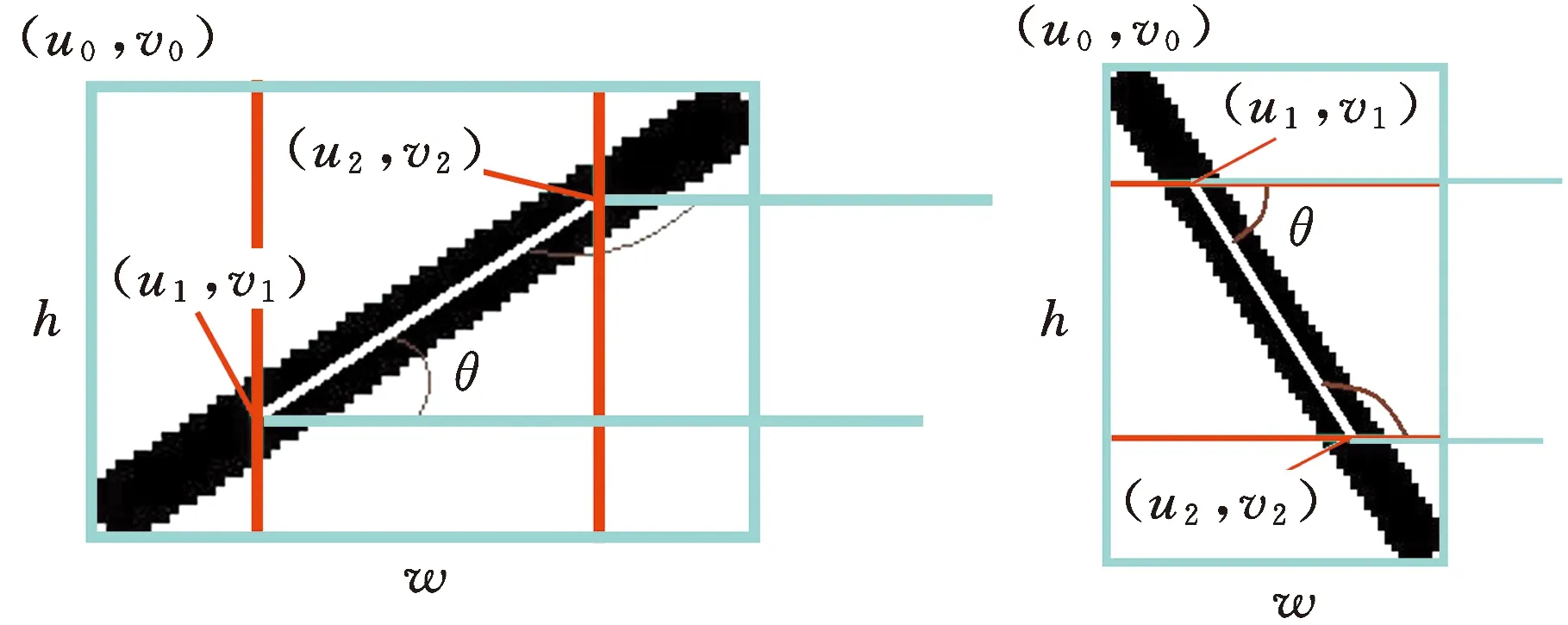
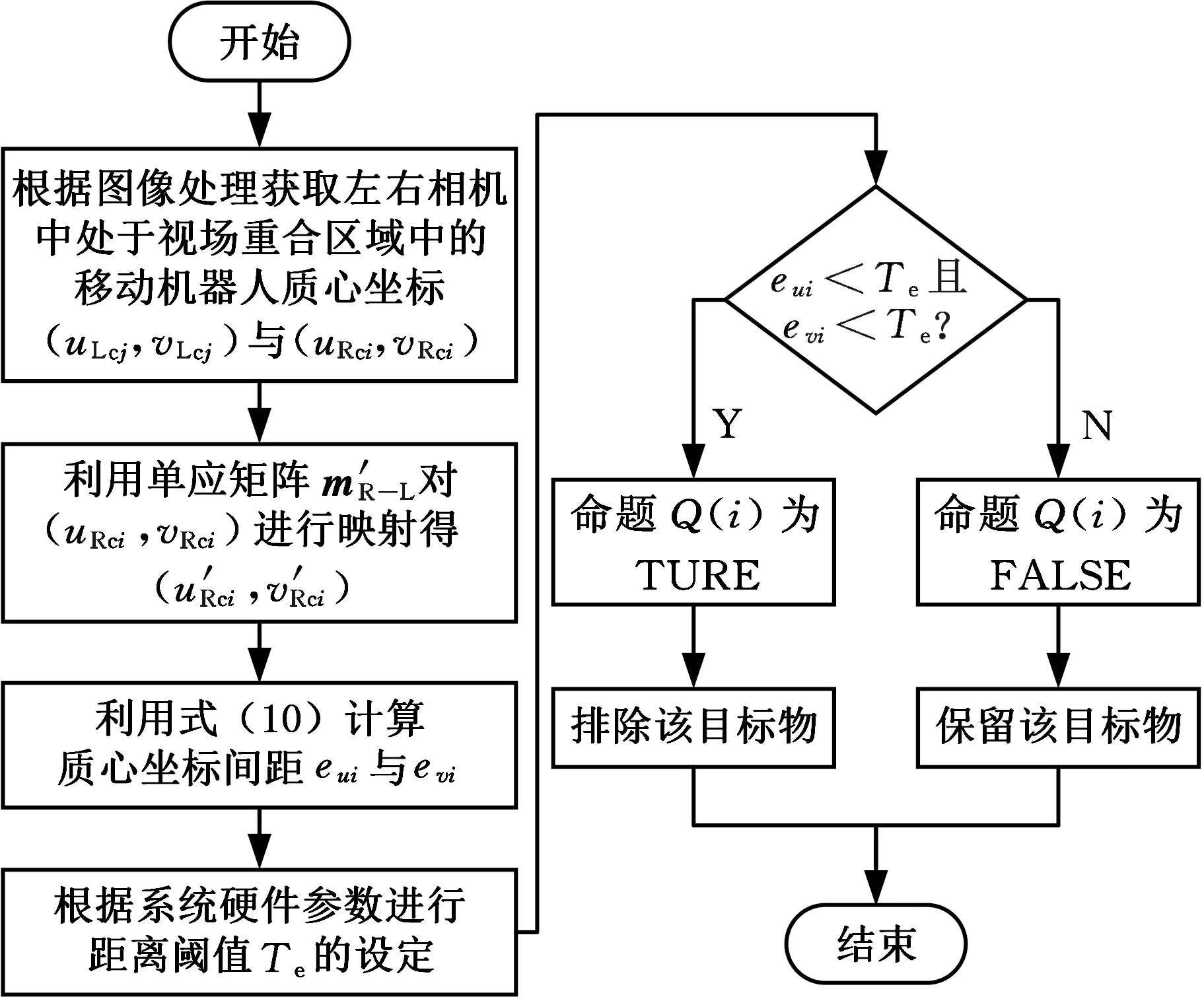
2.2 跨視場同名目標檢測算法
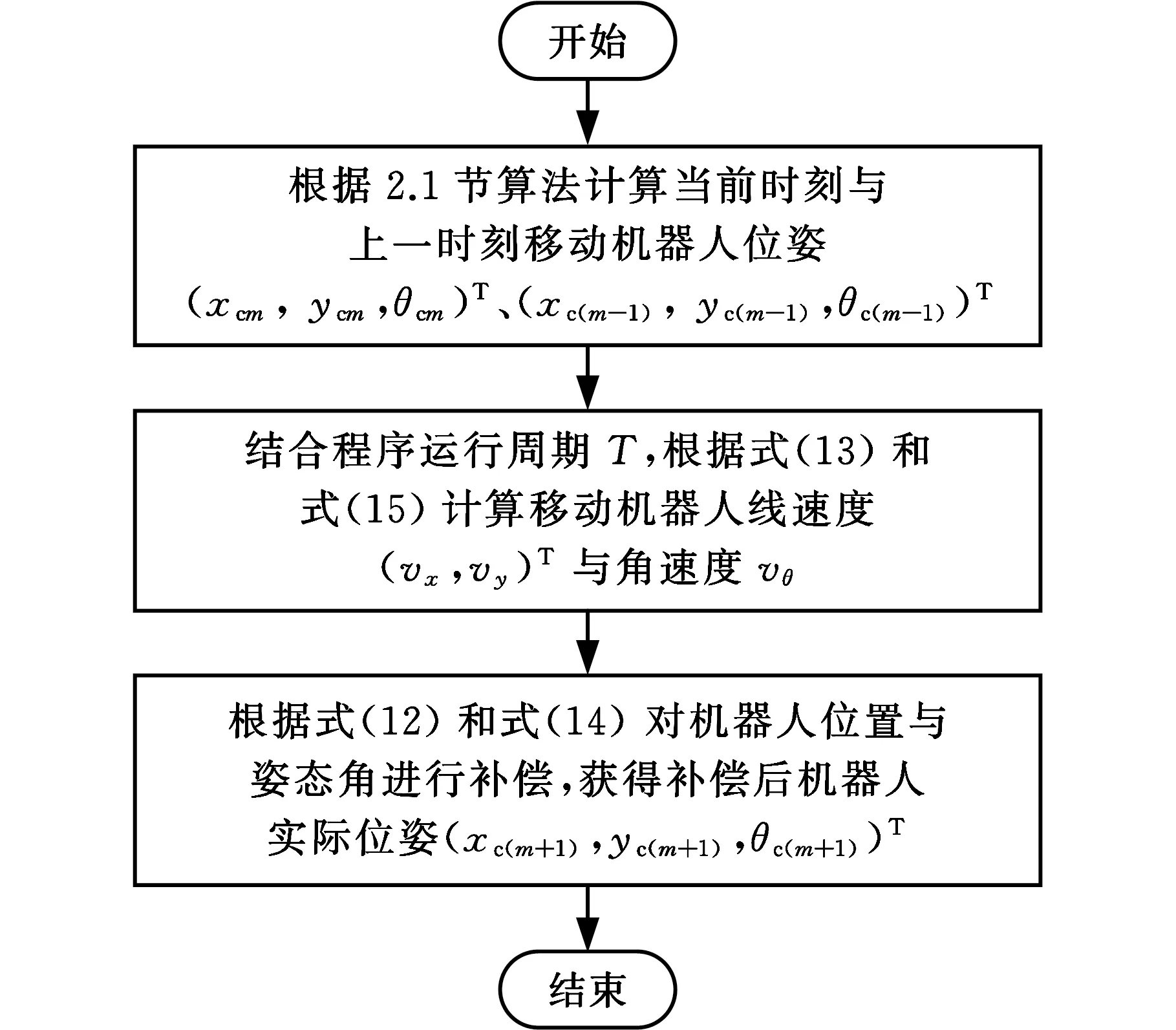
2.3 動態定位誤差補償算法
3 定位系統實驗
3.1 移動機器人位姿定位實驗

3.2 跨視場同名目標物檢測實驗


3.3 移動機器人定位動態誤差補償實驗

4 結論

