考慮部件不確定性的發動機性能裕度設計方法

計自飛，韓文俊，李瑞軍，閻巍

（中國航發沈陽發動機研究所，沈陽 110015）

0 引言

在航空發動機的加工、裝配、使用過程中均會產生部件和系統性能的不確定性，各部件性能不確定性累積疊加會導致發動機總體性能的非確定性。尤其是在極端和惡劣工作條件下，很小的部件性能偏差都將對整機性能產生極大影響[1]。在發動機研制初期就應充分考慮不確定性問題。為了保證性能達標，以往的做法是在發動機總體指標上直接留出一定裕度，該裕度的取值往往依賴于工程經驗。對于新研發動機，由于新技術的應用，尚無足夠的經驗，裕度選取過大，將會導致過大的冗余設計，進而造成其他性能損失；裕度選取過小，則發動機總體性能仍存在較高的不達標風險。

部件參數不確定性對發動機總體性能的影響的量化分析，可以通過蒙特卡羅模擬（Monte Carlo Simulation，MCS）方法實現。Kurzke[2]利用蒙特卡羅方法模擬了燃氣渦輪發動機的性能表征；Mavris等[3-5]利用概率方法研究了部件性能對發動機循環參數選取的影響，為發動機循環參數穩健性設計提供了參考；Kestner等[6-7]建立了響應面模型、貝葉斯網模型、神經網絡模型等來發展穩健設計方法；陳敏等[8]利用蒙特卡羅模擬開展了部件性能不確定性在渦軸發動機性能分析中的量化研究；唐海龍等[9]基于渦軸發動機部件不確定性的量化分析模型，研究了控制規律變化和性能蛻化對渦軸發動機性能達標概率的影響；趙運生[10]以大涵道比渦扇發動機為研究對象，基于蒙特卡羅模擬研究了部件性能不確定性對整機性能達標概率的影響。以上研究主要基于發動機非線性模型開展，加上蒙特卡羅模擬需要足夠大的樣本數量才能獲得有意義的結果[11]，但過大的計算量和計算時間在工程上難以接受。

本文以混合排氣渦扇發動機為研究對象，建立了航空燃氣渦輪發動機性能參數裕度需求的確定方法。

1 數學物理模型

1.1 基本思路

部件和系統的不確定性可以通過部件參數表征，例如，效率、面積等。概率密度函數用于模擬各部件和系統性能的不確定性，使其能夠在確定性的總體性能分析模型中傳播。部件參數不確定性對發動機總體性能參數的影響分析原理如圖1所示。

圖1 部件參數不確定性對整機性能的影響分析原理

從圖中可見，性能參數的不確定性客觀存在。總體性能穩健設計的目的就是提高性能參數達標的置信度。考慮部件不確定性的發動機性能裕度設計實現途徑如圖2所示。從圖中可見，單純減小性能參數的不確定性，不能提高參數置信度；而通過在性能參數上留出合理的裕度，可以實現性能參數置信度的提高。可見，根據置信度需求確定合理的參數裕度需求是穩健設計的關鍵環節。

圖2 考慮部件不確定性的發動機性能裕度設計實現途徑

1.2 計算模型

根據分析，開展考慮部件不確定性的發動機性能裕度設計的基本步驟包括：不確定性定義→不確定性傳播→不確定性量化→總體參數裕度確定，如圖3所示。

圖3 考慮部件不確定性的發動機性能裕度設計方法

（1）不確定性定義。

不確定性定義就是確定各部件參數的概率密度函數。概率密度函數用于模擬各部件和系統性能的不確定性，使其能夠在確定性的總體性能分析模型中傳播。假定標準正態分布N（0，1）的概率密度函數可表示為

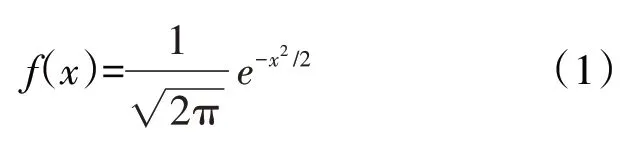
假定各部件和系統參數不確定性分布符合正態分布，則其性能參數偏差量的樣本N為

式中：μ為樣本的均值；σ為樣本的標準差。

（2）不確定性傳播。

部件和系統參數不確定性的傳播通過發動機的數學物理模型實現。本文以小涵道比混合排氣渦扇發動機為研究對象。根據部件共同工作原理[12-13]，發動機在非設計點工作時必須滿足6個平衡方程，即低壓軸功率、高壓軸功率、混合室內外涵靜壓、燃燒室與高壓渦輪流量、高壓渦輪與低壓渦輪流量、低壓渦輪與尾噴管流量平衡方程。以上6個平衡方程構成發動機穩態模型的數學基礎，寫成參數形式為

式（3）可通過Newton-Raphson方法迭代求解。寫成微分形式為

用差商代替微商，則式（4）變為

式中：M為6階系數矩陣。

由式（5）得到ΔX后，k+1次迭代的變量值修正為

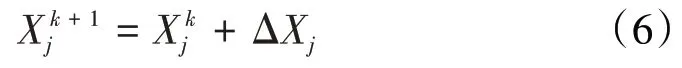
如此反復，不斷修正獨立變量的值，直至平衡方程誤差滿足設定精度要求。

下面通過與GasTurb 13軟件計算結果的比較，驗證根據上述方法建立的發動機模型的精度和可靠性。對于總壓比為32、涵道比為0.4、渦輪前溫度為1800 K的混合排氣渦扇發動機，在地面起飛狀態下，保持推力恒定，開環調整中間狀態噴管喉部面積，則不同面積對應的涵道比計算結果見表1。通過對比可見，本文模型計算結果與GasTurb計算結果的誤差均在1%以內，說明本文所建模型合理、可行，且具有較高精度，可完成部件和系統參數不確定性的傳播和量化。

表1 發動機非線性模型驗證

（3）不確定性量化。

蒙特卡羅模擬是研究不確定性量化的經典方法。采用蒙特卡羅方法量化模型不確定性時，樣本數量要足夠大，才能得到可靠的結果[11]。因此，采用傳統的航空燃氣渦輪發動機的總體性能分析模型作為目標函數會導致計算量極大。由文獻[14]可知，生產、裝配等因素導致的部件效率等參數的偏差量均在±1%以內。部件和系統偏差在±1%以內時，基于建立的發動機非線性性能仿真模型獲得的發動機地面起飛狀態性能參數對部件參數的敏感性分析結果如圖4所示。從圖中可見，在小偏差范圍內，整機性能隨各部件和系統參數偏差量的變化基本呈線性變化，曲線的斜率越大，說明性能參數對該部件參數偏差量越敏感。這一點可以通過將發動機性能參數關于部件和系統參數的表達式進行Taylor展開，并略去高階項的方法驗證。因此，可以利用總體性能參數對部件參數的敏感性系數矩陣（見表2）替代航空發動機非線性模型，開展部件參數不確定性的量化分析，從而在保證精度的同時，大大減小計算量。該方法稱為敏感性系數矩陣方法（Sensitivity Coefficient Matrix Method，SMM）。

圖4 發動機總體參數對部件參數的敏感性

各部件和系統參數的綜合影響用和方根（Root Sum Square，RSS）方法求解（表2）。表中部件參數偏差量一欄換成不同置信度下各部件參數相比于均值的最大變化量的絕對值，即可得到不同置信度對應的發動機總體性能參數的最大偏差量。根據和方根方法的理論可知，各部件參數偏差量的置信度直接影響發動機總體參數偏差量的置信度。為了評估表2中敏感性系數矩陣的可靠性，利用成熟軟件GasTurb 13計算了相同輸入條件下的計算結果，見表3。表2、3對應單項與和方根結果的偏差均在0.03%以內，從而證實了表1中的敏感性系數矩陣的可靠性。

表2 總體性能參數對部件參數的敏感性系數矩陣（本文方法）

表3 總體性能參數對部件參數的敏感性系數矩陣（GasTurb 13）

1.3 模型驗證

為了驗證上述方法的合理性，對采用蒙特卡羅法獲得的發動機推力和耗油率概率分布與采用敏感性系數矩陣方法獲得的結果進行對比，2種方法獲得的發動機總體參數概率分布如圖5所示，其中蒙特卡羅法的樣本容量選取為20000。從圖中可見，2種方法獲得的發動機總體性能參數概率分布吻合良好，從而證明了敏感性系數矩陣方法的合理性，可用于不確定性的量化和總體性能參數裕度需求的確定。

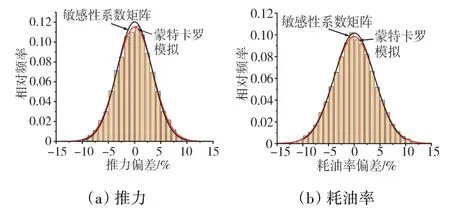
圖5 2種方法獲得的發動機總體參數概率分布

2 結果與討論

與試驗測試不同，無論如何精確和復雜的性能分析模型都無法自動考慮不確定性的影響。為此，將不確定分析融入發動機性能分析模型，可為發動機性能不確定性分析以及性能裕度設計提供依據[15]。按照確定性模型開展方案設計，只能保證發動機平均性能達標，即發動機性能達標的置信度只有50%，這顯然不滿足項目要求。為此，在設計中必須留出一定的性能裕度，使得發動機性能參數的置信度達到更高值。以給出的小涵道比渦扇發動機為研究對象，選取地面起飛狀態為設計點，部件和系統參數的偏差量按照文獻[14]中的方法考慮，進一步研究發動機總體性能參數裕度需求的確定及其影響因素。

2.1 總體性能達標置信度對裕度需求的影響

根據部件和系統參數的不確定性分布，采用敏感性系數矩陣方法得到發動機總體性能參數的不確定性分布，為簡化分析，本文使用參數的相對偏差量代替參數的絕對量進行分析，如圖6、7所示。對于推力而言，達標的標準是樣本值大于目標值；而對于耗油率而言，達標的標準是樣本值小于目標值。因此二者的累積概率曲線的形狀不同。

從圖中可見，性能參數達到某一置信度對應的數值相比于均值（即性能指標）的偏差即可作為該性能參數的設計裕度。采用SMM和MCS方法計算得到的不同置信度對應的地面起飛狀態總體參數裕度需求見表4、5。從表中可見，采用2種方法得到的計算結果吻合良好，進一步證實了本文建立的敏感性系數矩陣方法的有效性。總體性能參數滿足設計要求的置信度越高，其需要留出的裕度越大。這一點可以由圖6（b）和圖7（b）直觀解釋，圖中不同顏色的曲線分別代表不同置信度下的推力不確定性分布。與基準發動機（參數裕度為0，性能達標置信度50%）的偏差越大，意味著裕度需求越大，則樣本在性能達標區的占比越大，即性能達標的置信度越高。

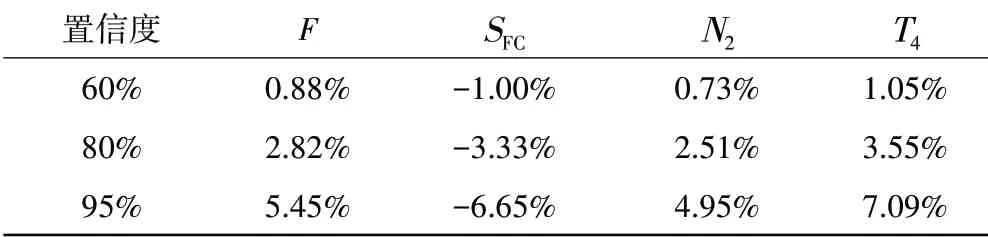
表4 不同性能置信度對應總體參數裕度需求（SMM）

圖6 性能達標置信度對推力裕度需求的影響

圖7 性能達標置信度對耗油率裕度需求的影響

表5 不同性能置信度對應總體參數的裕度需求（MCS）

在地面起飛狀態下，當發動機性能指標的置信度設置為60%時，推力和耗油率裕度需求分別為0.88%和-1.00%；當發動機性能指標的置信度設置為80%時，推力和耗油率裕度需求分別為2.82%和-3.33%；當發動機性能指標的置信度設置為95%時，推力和耗油率裕度需求分別為5.45%和-6.65%。需要注意的是，以上定量結論是基于本文設定的發動機循環參數計算得出的，該方法可推廣應用于不同發動機，具體量化結果需要根據相應發動機的循環參數進行評估。

2.2 部件參數達標置信度對裕度需求的影響

壓氣機效率不確定性分布的標準差與置信度的關系如圖8所示。在某一特定區間內，部件參數不確定分布的標準差越小，則參數落入該區間的置信度越高。因此，可用部件參數不確定性分布的標準差來表征部件參數的置信度。以前文所用各部件參數不確定性分布的標準差為基準，在此基礎上乘以不同系數，構成3種不同的部件參數置信度。考慮將發動機總體性能參數的置信度目標設定為80%，則按照前文確定性能參數裕度的方法，利用2種方法計算的不同部件參數置信度對應的發動機地面起飛狀態性能參數裕度設計結果見表6、7。

圖8 壓氣機效率不確定性分布的標準差與置信度的關系

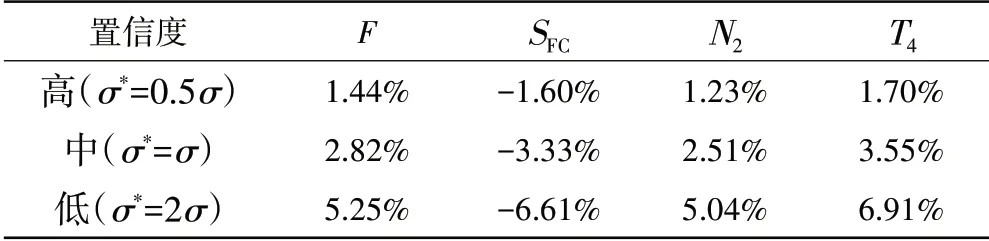
表6 不同部件參數置信度對應總體參數裕度需求（SMM）

表7 不同部件參數置信度對應總體參數裕度需求（MCS）

從表中可見，2種方法的計算結果吻合良好，進一步證實了本文建立的敏感性系數矩陣方法的有效性。部件參數置信度對推力和耗油率裕度需求的影響如圖9、10所示。根據定量結果，部件參數滿足設計目標的置信度越高，總體性能參數需要留出的裕度越小。這一點的物理含義可以通過圖9（b）和圖10（b）進行解釋。當總體性能參數達標的置信度相同時，總體性能參數的概率密度曲線越“瘦高”，則該分布的均值與性能指標的差值越小，意味著性能參數的裕度需求越小。就正態分布而言，概率密度曲線越“瘦高”，則要求各部件和系統參數的標準差越小，意味著部件和系統參數達標的置信度越高（圖8）。

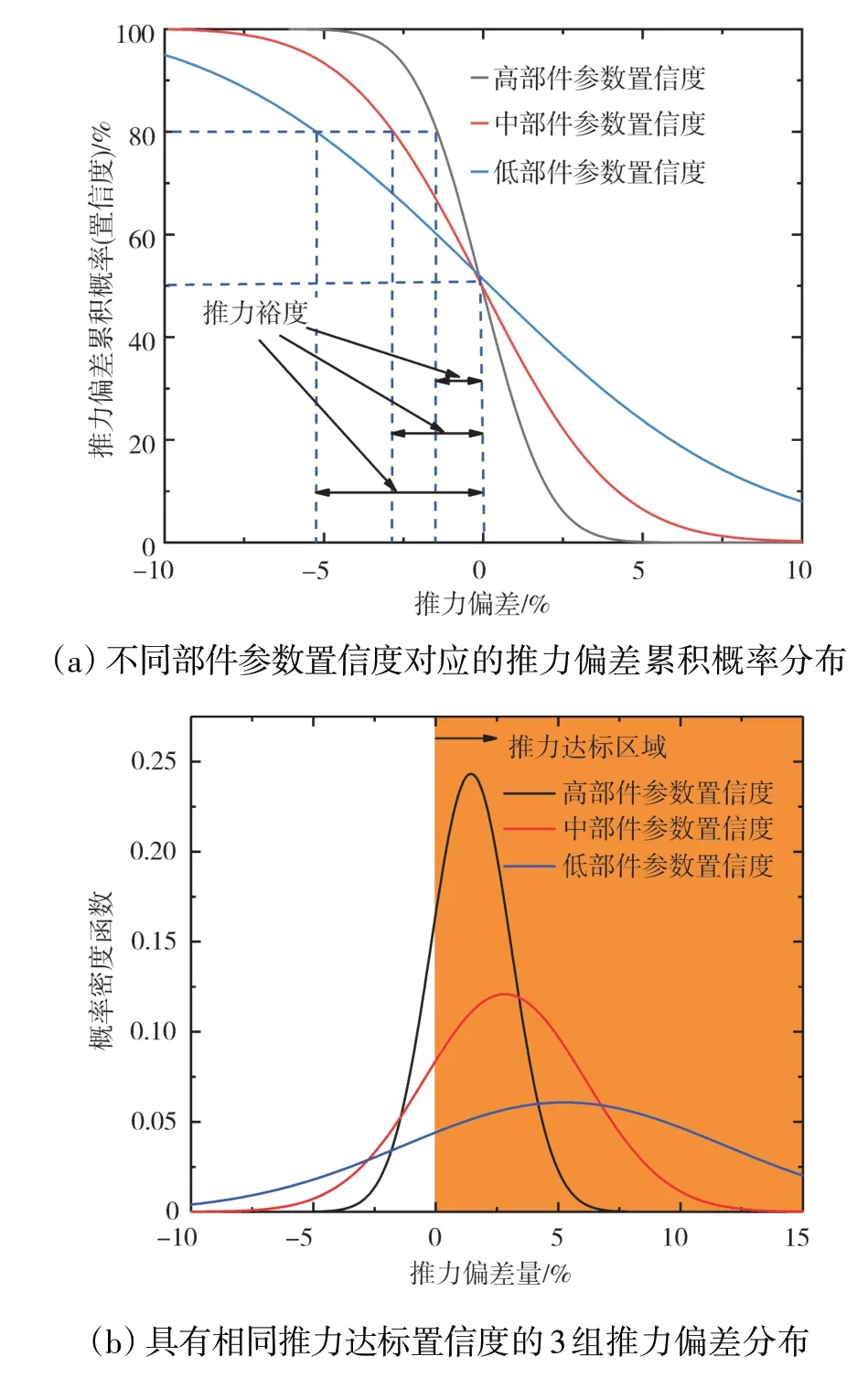
圖9 部件參數置信度對推力裕度需求的影響

圖10 部件參數置信度對耗油率裕度需求的影響

在地面起飛狀態下，將各部件參數的標準差增大1倍，則推力裕度需求增加86%，耗油率裕度需求增加98%；將各部件參數的標準差減小50%，則推力裕度需求減小49%，耗油率裕度需求減小52%。該定量結論是基于本文設定的發動機循環參數計算得出的，該方法可推廣應用于不同的發動機，具體量化結果需要根據相應發動機的循環參數進行評估。

上述部件參數不確定性對發動機性能參數影響分析的結果，為發動機總體性能參數裕度設計提供了理論依據。性能參數裕度需求的確定，需要考慮各方面的因素來綜合確定。在方案設計初期，總體性能參數裕度的設計需要考慮發展潛力、性能衰退、安裝損失、部件參數不確定性等多方面[16-18]，本文主要關注考慮部件參數不確定性的發動機性能參數裕度設計。對于輸出功率的地面燃機，可以通過放大尺寸來留出足夠的功率裕度；而提供推力的航空發動機，其推力裕度需求會受到質量和迎風面積的嚴格限制，考慮到競爭性采購等因素，耗油率指標的裕度也不宜過大。

3 結論

（1）在加工、裝配等環節導致的部件和系統參數偏差范圍內，航空發動機總體性能偏差量隨各部件和系統參數偏差量的變化基本呈線性變化，曲線的斜率越大，說明性能參數對該部件偏差量越敏感。耗油率對于部件效率和引氣比例的偏差更加敏感，而推力對于尾噴管喉部面積的偏差更加敏感。

（2）對于各部件參數的不確定性滿足正態分布，且各參數之間不相關的情形，部件參數不確定性對發動機總體性能參數的影響量化分析可通過敏感性系數矩陣方法實現。由于部件參數不確定性導致的總體性能參數偏差分布同樣滿足正態分布，并且部件參數的置信度決定了發動機總體性能參數的置信度。

（3）部件參數不確定分析結果為總體性能參數裕度設計提供了依據。部件參數滿足設計目標的置信度越高，總體性能參數需要留出的裕度越小。部件參數置信度可由不確定性分布的標準差來表征，對于本文的算例發動機，在地面起飛條件下，若部件參數分布的標準差增大1倍，則推力裕度需求增加86%，耗油率裕度需求增加98%；若部件參數分布的標準差減小50%，則推力裕度需求減小49%，耗油率裕度需求減小52%。

（4）總體性能參數滿足設計要求的置信度越高，其需要留出的裕度越大。在地面起飛條件下，推力指標置信度分別達到60%、80%和95%對應的裕度需求分別是0.88%、2.82%和5.45%；耗油率指標置信度分別達到60%、80%和95%對應的裕度需求分別是-1.00%，-3.33%和-6.65%。

利用本文所建立的方法，可以在計算量較小的前提下獲得考慮部件參數不確定性的發動機總體性能裕度選取值。但本方法僅適用于部件和系統參數的不確定滿足正態分布，且各部件參數不相關的情況。若存在某一部件參數的不確定性為非對稱分布，則本方法不再適用，需要借助蒙特卡羅模擬來開展相關研究。同時，本文重點討論原理和方法，定量結果主要基于算例發動機工作參數得出，若要推廣用于其它發動機，則需更新算例發動機工作參數。