基于Dynamo的熱力管道絕熱層經濟厚度計算
趙霄強
(上海市政工程設計研究總院集團第十市政設計院有限公司,甘肅 蘭州 730000)
1 引言
目前,工程中管道絕熱層經濟厚度通常通過查表、查圖確定,然而工程圖表是在一定的外部條件下編制的,工程人員在應用時必須注意其相應的適用條件,當不滿足適用條件時,必須按照標準要求重新計算[1]。同時,性能優良的新型保溫材料不斷涌現[2],并得到應用[3-4],需要對絕熱層經濟厚度進行重新核定[5]。然而,按照規范要求手工計算管道絕熱層經濟厚度困難較大,利用有限元軟件對管道傳熱進行分析的流程相對復雜[6]。
Dynamo是一款基于Revit的計算機輔助設計工具,該工具具有強大的列表處理功能。本研究利用Dynamo對管道絕熱層經濟厚度進行計算,將計算結果與圖集表格進行對比,并對絕熱層經濟厚度的影響因素進行分析。
2 管道絕熱層經濟厚度的計算方法
根據規范要求,圓形管道絕熱層經濟厚度可按式(1)進行計算[7]。
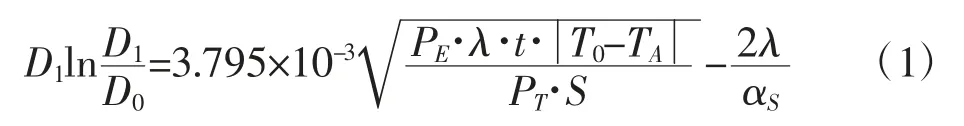
式中:D1為絕熱層外徑,m;D0為管道外徑,m;PE為能量價格,元/GJ;λ為絕熱材料在平均溫度下的導熱系數,W/(m·℃);T0為管道外表面溫度,℃;Ta為環境溫度,℃;PT為絕熱層單位造價,元/m3;S為絕熱工程投資年攤銷率,%;αs為絕熱層外表面放熱系數,W/(m2·℃)。
圖集中給出的絕熱材料導熱系數可以簡化為式(2)的形式[8],通常與保溫材料廠家提供的材料導熱系數線性回歸公式相一致。

式中:Tm為絕熱層內、外表面溫度的算術平均值,℃;a、b為常量,根據絕熱材料種類和使用溫度確定。其中,Tm可根據式(3)計算。

式中:TS為絕熱層外表面溫度,℃。
絕熱層外表面放熱系數αS按照式(4)進行計算。

式中:αr為絕熱層外表面材料輻射換熱系數,W/(m2·℃);αc絕熱層外表面對流換熱系數,W/(m2·℃)。
αr可按式(5)計算,見式(5):
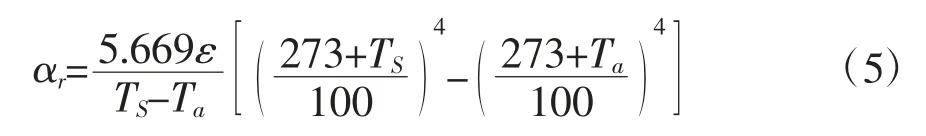
絕熱層外表面對流換熱系數αc與室外年平均風速W相關,當WD1≤0.8 m2/s時,αc按式(6)計算。

當WD1>0.8 m2/s時,αc按式(7)計算。

式(1)為隱函數形式,無法直接求解;導熱系數、外表面換熱系數與絕熱層外表面溫度存在函數關系,更增加了求解的難度。在管道絕熱層經濟厚度的計算中需要大量迭代,手工計算幾乎無法完成。
3 利用Dymamo計算絕熱層經濟厚度的思路
Dynamo是一款可視化編程軟件,其對列表有強大的編輯、處理能力[9],本研究正是利用該軟件的列表處理能力來解決絕熱層經濟厚度計算的問題。
在管道穩態傳熱條件下,通過絕熱層的熱流量和通過表面傳熱的熱流量相等[10],即滿足式(8)要求。
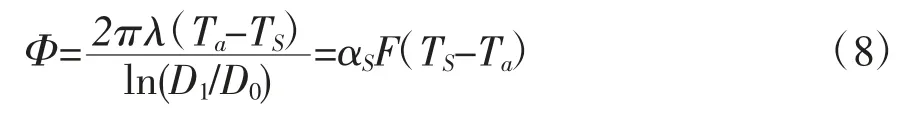
當環境溫度、風速一定時,式(8)存在無窮組解,給定一個絕熱層外徑D1,即可求出一組解{D1,λ,αS,TS,Φ...}。在無窮組解中,存在一組解使式(1)左右兩側差值的絕對值最小,該組解所對應的D1即為管道絕熱層經濟厚度下的絕熱層外徑,從而可求出絕熱層經濟厚度。為了控制式(8)的解的數量,需要對絕熱層外徑D1、絕熱層外徑梯度ΔD1、絕熱層外表面溫度的最大值TSmax、絕熱層外表面溫度梯度ΔTS作出一定限制。
3.1 絕熱層外徑列表LD1
在工程中,管道絕熱層外徑并不是無窮大的,為了減少絕熱層外徑列表容量,需要給定其上限D1max,D1max=A×D0(A>1)。在給定A值情況下,當式(1)兩側差值的絕對值的最小值對應的序號加1小于列表項數時,則式(1)存在解,即設定的最大絕熱層外徑D1max大于絕熱層經濟外徑;否則,式(1)不存在解,即設定的D1max小于絕熱層經濟外徑,此時要增大A值,直至式(1)存在解。
絕熱層外徑梯度ΔD1對LD1的容量影響很大,ΔD1越小,列表容量越大,計算出的結果越精確,通常當ΔD1=1 mm時,即可滿足工程計算要求。
通過以上分析,對于φ27的管道(DN20),當A=2時,ΔD1=1 mm時,最終形成的列表為{28、29、30...52、53、54}mm,如圖1所示。
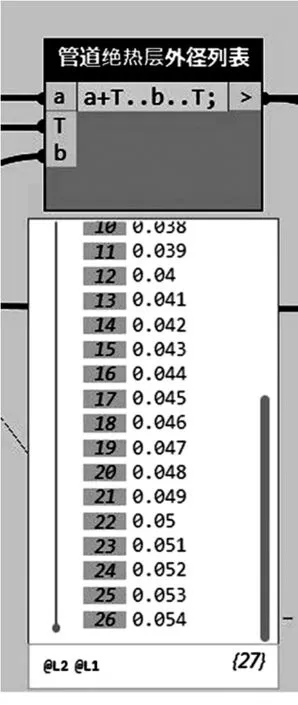
圖1 絕熱層外徑列表LD1
3.2 絕熱層外表面溫度列表LTS
在管道采取保溫措施后,TS通常會小于防燙傷溫度,為了減少LTS容量,需要給定其上限TSmax(T0>TSmax>Ta)。
同時,絕熱層外表面溫度梯度ΔTS對LTS容量的影響也很大,ΔTS越小,列表容量越大,計算出的結果越精確,通常當ΔTS=1 ℃時,即可滿足工程計算要求。
通過上述分析,當T0=80 ℃,TSmax=65 ℃,Ta=20 ℃,ΔTS=1 ℃時,最終形成的列表為{64、63、62...23、22、21}mm,如圖2所示。
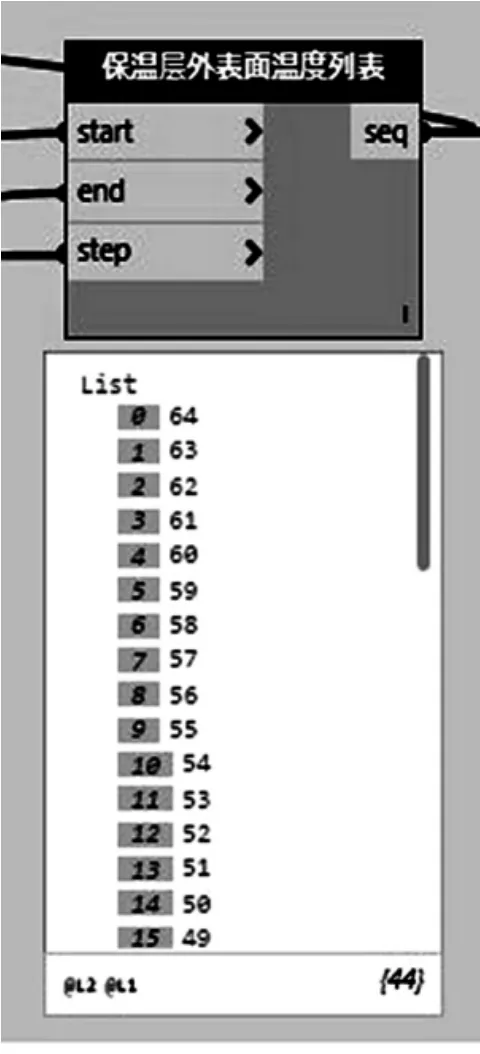
圖2 絕熱層外表面溫度列表LTS
3.3 保溫層導熱系數列表Lλ
在已知T0及LTS時,根據式(2)可計算出Lλ,如圖3所示。

圖3 保溫層導熱系數列表Lλ
3.4 絕熱層外表面換熱系數列表LαS
在已知年平均風速W、絕熱材料外表面絕熱黑度ε、Ta下,并結合Lλ、LTS,根據式(4)可計算出LαS,如圖4所示。需要注意的是LαS為二維列表,其他列表為一維列表,根據式(8)計算熱流量時,需要將列表轉換為相同的維度。
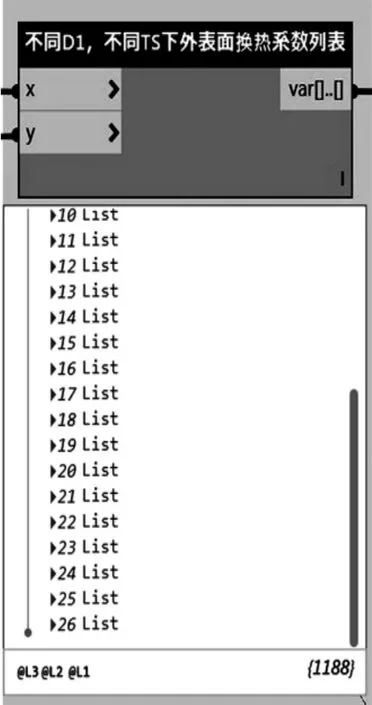
圖4 絕熱層外表面換熱系數列表LαS
3.5 熱流量列表Lφ1、Lφ2
在已知LTS、Lλ、LD1、D0、T0時,由式(8)可計算出通過絕熱層外表面因為導熱而產生的熱流量列表Lφ1;在已知LαS、LTS、T0、LD1時,由式(8)可計算出通過絕熱層外表面因為對流、輻射而產生的熱流量列表Lφ2。Lφ1與Lφ2差值的絕對值最小時(如圖5所示),所對應的溫度,即為在一定絕熱層外徑D1下的絕熱層外表面溫度TS。

圖5 Lφ1與Lφ2差值的絕對值
以上是求管道傳熱的通用過程,Dynamo可將以上過程封裝為一個節點,可簡化程序,并增強程序的可讀性,如圖6所示。

圖6 封裝節點
3.6 求解絕熱層經濟厚度下的絕熱層外徑
在已知PE、t、PT、S、D0時,將以上列表帶入式(1),滿足等式兩側差值最小時的D1即為絕熱層經濟厚度下的絕熱層外徑,進而可求出絕熱層經濟厚度。
4 程序計算結果與圖集的對比
為了驗證程序的正確性,本研究分別以閉孔橡塑泡沫絕熱層和硅酸鋁棉絕熱層為例,計算在不同熱價、不同介質溫度、不同運行時間下的絕熱層經濟厚度,并與圖集進行對比,如圖7—圖8所示。
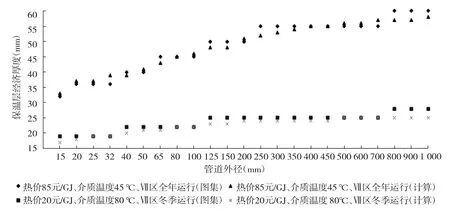
圖7 閉孔橡塑泡沫絕熱層在不同熱價、介質溫度、運行時間時程序計算值與圖集值的對比
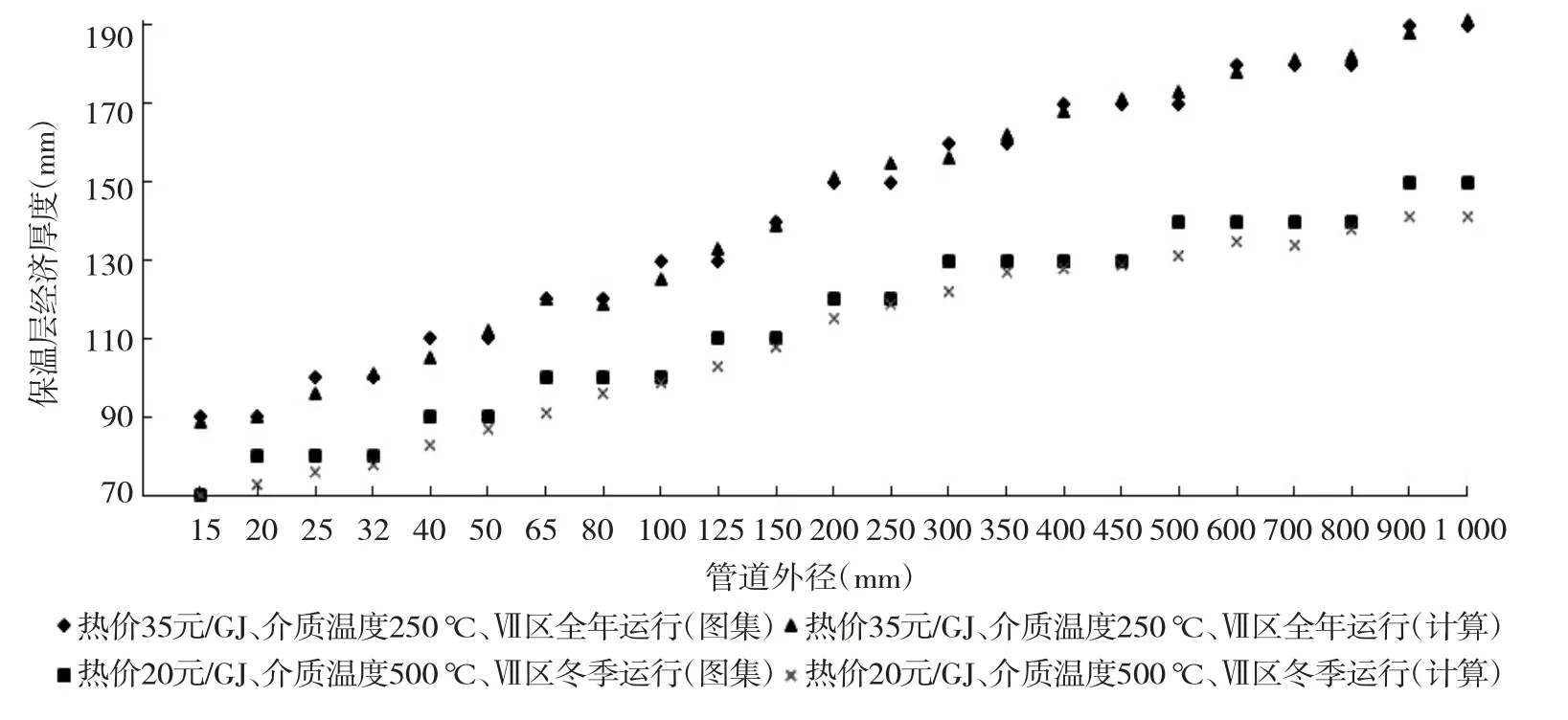
圖8 硅酸鋁棉絕熱層在不同熱價、介質溫度、運行時間時程序計算值與圖集值的對比
圖集中給出了計算絕熱層厚度的圓整規則,閉孔橡塑泡沫絕熱層和硅酸鋁棉絕熱層的厚度檔次劃分,見表1。

表1 閉孔橡塑泡沫絕熱層和硅酸鋁棉絕熱層的厚度檔次劃分 單位:mm
其中,閉孔橡塑泡沫絕熱層δ最小厚度為16 mm,當δ≤28 mm時,以3 mm為一檔;當28 mm<δ≤40 mm時,以4 mm為一檔;當δ>40 mm時,以5 mm為一檔。硅酸鋁棉絕熱層厚度δ最小厚度為20 mm,以10 mm為一檔。
由圖7可以看出,絕熱層厚度區間內,程序計算結果與圖集值的差值Δδ≤2 mm,小于各區間的最大檔次值3 mm。
由圖8可以看出,絕熱層厚度區間內,程序計算結果與圖集值的差值Δδ≤9 mm,小于各區間的最大檔次值10 mm。
通過以上對比可以看出程序計算結果與圖集值偏差不大,可以在工程中用于計算不同情況下的絕熱層厚度。
5 絕熱層經濟厚度影響因素分析
由式(1)、(2)、(4)可以看出,影響絕熱層厚度的因素有D0、PE、T0、Ta、PT·S、W、t、λ。以下分別以硬質聚氨酯泡沫(a=0.024,b=0.000 14,PT=2 700元/m3)和巖棉板(a=0.036 4,b=0.000 18,PT=1 500元/m3)為絕熱層材料來分析D0、PE、T0、t、λ對絕熱層經濟厚度的影響。
由圖9可以看出,當管徑由DN200增加到DN1000時,硬質聚氨酯絕熱層厚度由41 mm增加到46 mm,增加5 mm,而巖棉絕熱層厚度由62 mm增加到72 mm,增加10 mm,巖棉絕熱層的增加厚度為聚氨酯的2倍。由以上分析可以得出,絕熱層經濟厚度隨著管徑的增大而增大;材料導熱系數越大,絕熱層經濟厚度隨管徑的變化越大。
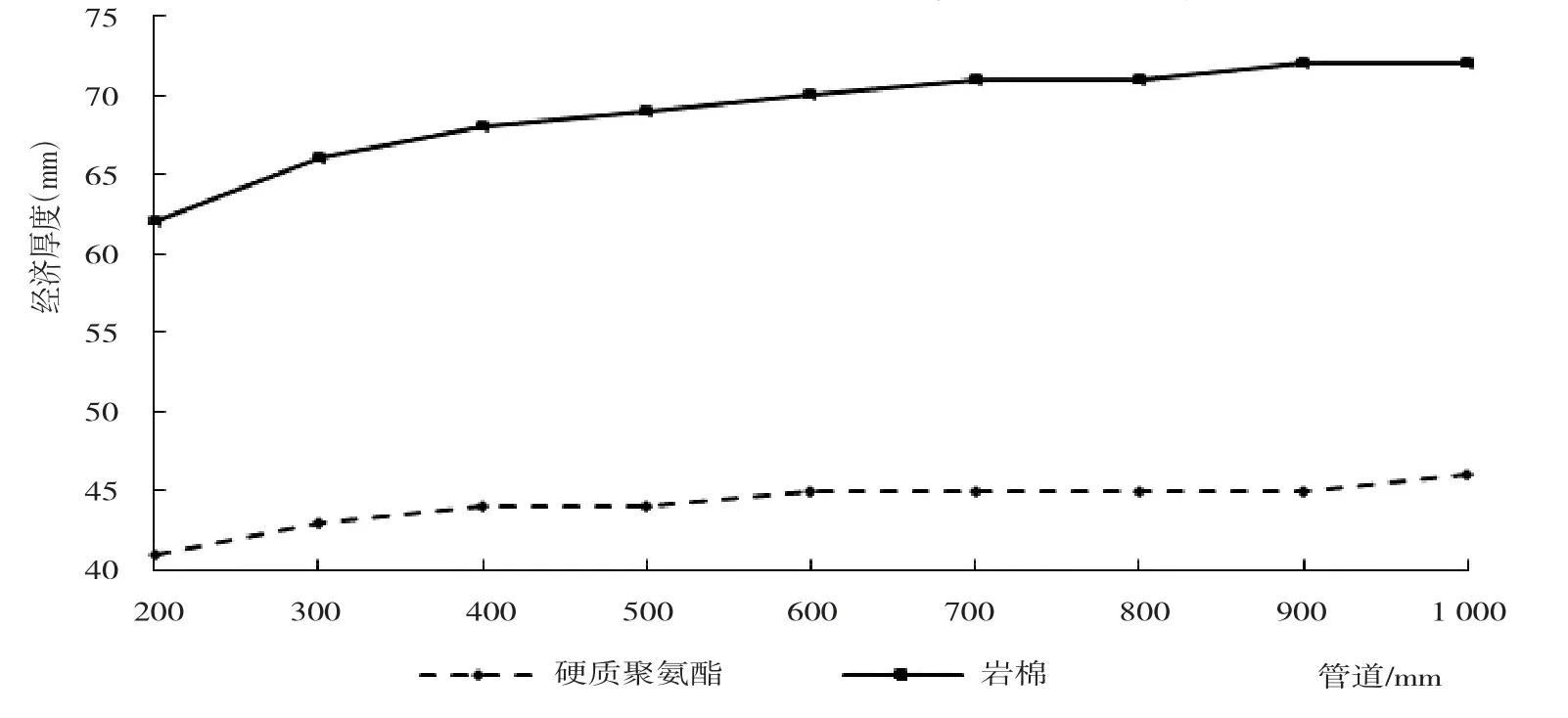
圖9 管徑對絕熱層經濟厚度的影響
由圖10可以看出,當能量價格由35元/GJ增加到75元/GJ時,對于DN200的管道,硬質聚氨酯絕熱層厚度由33 mm增加到47 mm,增加14 mm,而巖棉絕熱層厚度由51 mm增加到71 mm,增加20 mm,巖棉絕熱層的增加厚度為聚氨酯的1.4倍;對于DN1000的管道,硬質聚氨酯絕熱層厚度由37 mm增加到53 mm,增加16 mm,而巖棉絕熱層厚度由58 mm增加到84 mm,增加26 mm,巖棉絕熱層的增加厚度為聚氨酯的1.6倍。由以上分析可以得出,絕熱層經濟厚度隨著能量價格的提高而增大,且相同絕熱材料下,大尺寸管道的增加量大于小尺寸管道,相同尺寸管道下,導熱系數大的絕熱材料增加量大于導熱系數小的材料;相同的能量價格下,材料導熱系數越大、管徑越大,則其絕熱層經濟厚度大。
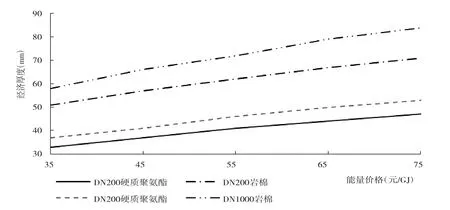
圖10 能量價格對絕熱層經濟厚度的影響
由圖11可以看出,當管道外表面溫度由80 ℃增加到200 ℃時,對于DN200的管道,硬質聚氨酯絕熱層厚度由35 mm增加到63 mm,增加28 mm,而巖棉絕熱層厚度由53 mm增加到93 mm,增加40 mm,巖棉絕熱層的增加厚度為聚氨酯的1.4倍;對于DN1000的管道,硬質聚氨酯絕熱層厚度由39 mm增加到74mm,增加35mm,而巖棉絕熱層厚度由62mm增加到115 mm,增加53 mm,巖棉絕熱層的增加厚度為聚氨酯的1.5倍。由以上分析可以得出,絕熱層經濟厚度隨著管道外表面溫度的升高而增大,且相同絕熱材料下,大尺寸管道的增加量大于小尺寸管道,相同尺寸管道下,導熱系數大的絕熱材料增加量大于導熱系數小的材料;相同的管道外表面溫度下,材料導熱系數越大、管徑越大,則其絕熱層經濟厚度越大。
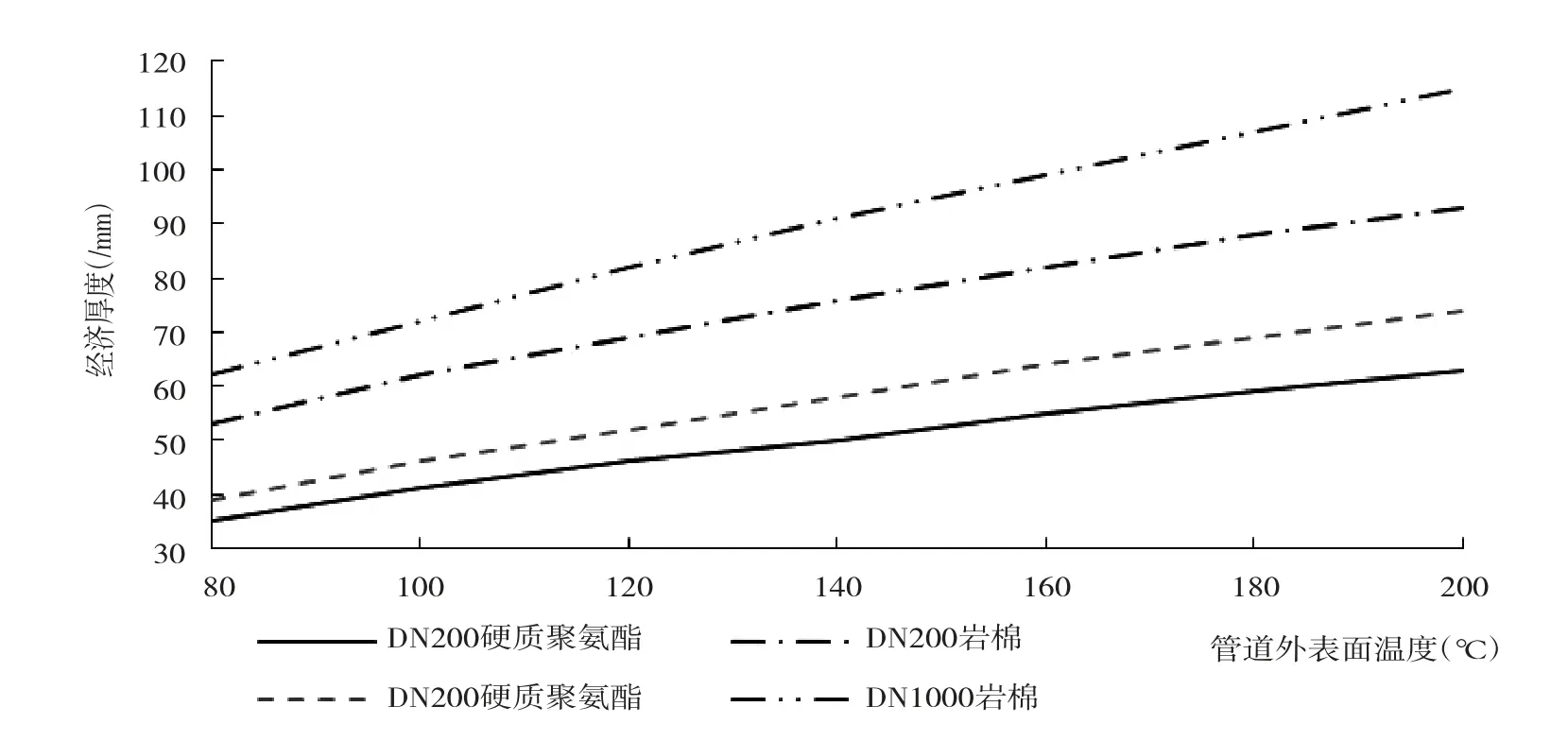
圖11 管道外表面溫度對絕熱層經濟厚度的影響
由圖12可以看出:年運行時間越長,絕熱層經濟厚度越大。當年運行時間由1 000 h增加到4 000 h時,對于DN200的管道,硬質聚氨酯絕熱層厚度由25 mm增加到47 mm,增加22 mm,而巖棉絕熱層厚度由39 mm增加到72 mm,增加33 mm,巖棉絕熱層的增加厚度為聚氨酯的1.5倍;對于DN1000的管道,硬質聚氨酯絕熱層厚度由27 mm增加到54 mm,增加27 mm,而巖棉絕熱層厚度由43 mm增加到85 mm,增加42 mm,巖棉絕熱層的增加厚度為聚氨酯的1.6倍。由以上分析可以得出,絕熱層經濟厚度隨著年運行時間的增加而增大,且相同絕熱材料下,大尺寸管道的增加量大于小尺寸管道,相同尺寸管道下,導熱系數大的絕熱材料增加量大于導熱系數小的材料;相同的年運行時間下,材料導熱系數越大、管徑越大,則其絕熱層經濟厚度越大。
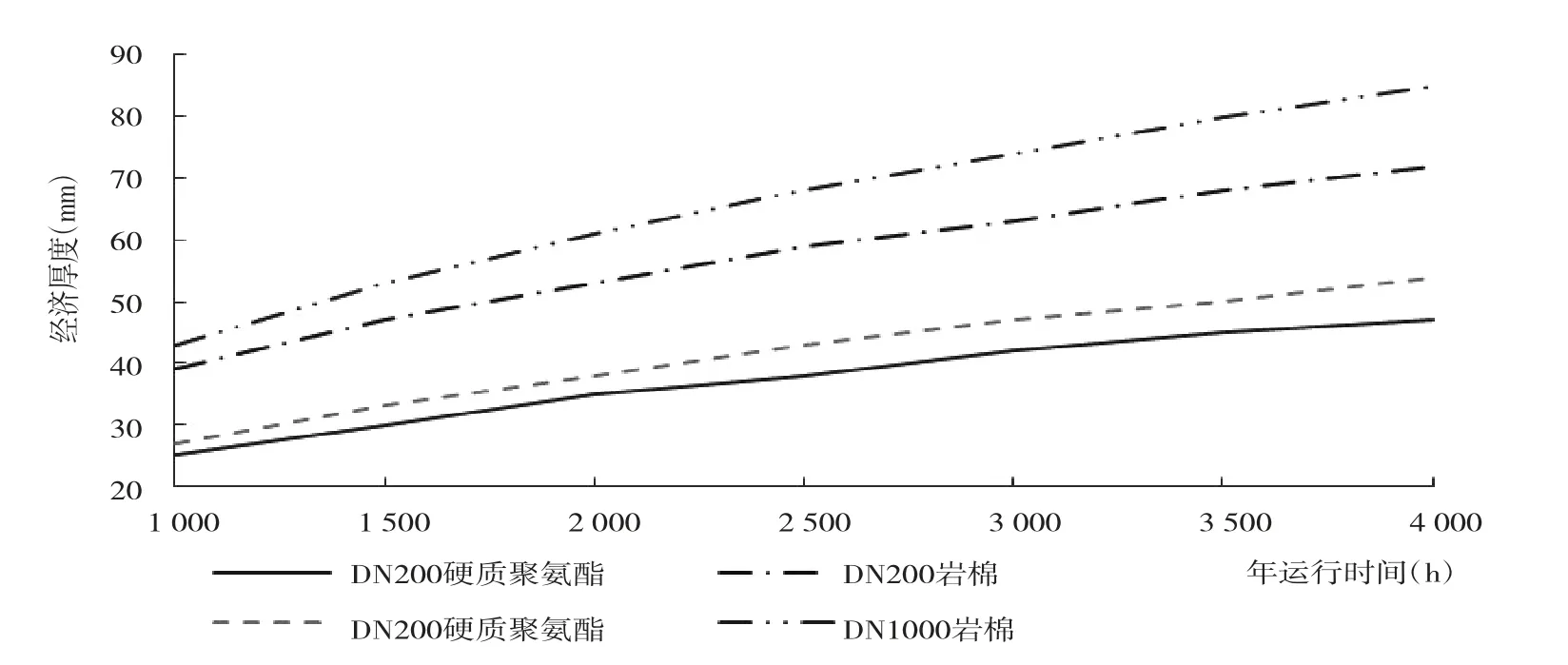
圖12 年運行時間對絕熱層經濟厚度的影響
由以上分析可總結出:絕熱層經濟厚度隨管徑、能量價格、管道外表面溫度、年運行時間、導熱系數的增大而增加,且相同絕熱材料下,大尺寸管道的增加量大于小尺寸管道,相同尺寸管道下,導熱系數大的絕熱材料增加量大于導熱系數小的材料。
6 結論與建議
(1)利用Dynamo計算管道絕熱層經濟厚度是可行的,為解決其他類似問題提供了一種思路。
(2)絕熱層經濟厚度隨管徑、能量價格、管道外表面溫度、年運行時間、導熱系數的增大而增加,且相同絕熱材料下,大尺寸管道的增加量大于小尺寸管道,相同尺寸管道下,導熱系數大的絕熱材料增加量大于導熱系數小的材料。
(3)導熱系數小的材料,絕熱層經濟厚度隨管徑的變化小。當管徑由DN200增加到DN1000時,巖棉絕熱層的增加厚度為聚氨酯的2倍。
(4)當能量價格由35元/GJ增加到75元/GJ時,對于DN200的管道,巖棉絕熱層的增加厚度為聚氨酯的1.4倍;對于DN1000的管道,巖棉絕熱層的增加厚度為聚氨酯的1.6倍。
(5)當管道外表面溫度由80 ℃增加到200 ℃時,對于DN200的管道,巖棉絕熱層的增加厚度為聚氨酯的1.4倍;對于DN1000的管道,巖棉絕熱層的增加厚度為聚氨酯的1.5倍。
(6)當管道年運行時間由1 000 h增加到4 000 h時,對于DN200的管道,巖棉絕熱層的增加厚度為聚氨酯的1.5倍;對于DN1000的管道,巖棉絕熱層的增加厚度為聚氨酯的1.6倍。

