一道向量題的多角度探析

江蘇省如皋中學 (745099) 王 濤

在教學過程中，對于一些典型問題，尤其是高考真題，如果我們能夠從不同角度思考，尋求不同的解法，以一題多解的方式尋求知識間的內在聯系，構建知識的網絡體系，加深對問題的本質認識，定會拓寬解題視野，發散解題思維，提升學習興趣，提高解題能力.本文是筆者對一道向量難題的研究，現與讀者分享交流.

1 試題呈現與分析

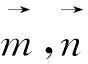
分析：該題形式上考查向量模和的最大值，考慮向量具有代數與幾何的雙重屬性，我們將問題轉化為函數問題處理，主要考查分析、解決向量問題的能力，強化對轉化與化歸、數形結合、消元與不等式求最值等數學思想方法的考查，體現了邏輯推理、數學運算等數學核心素養.試題結構雖簡單、明了，但內涵豐富，本文嘗試對該題從不同的角度予以思考，給出不同的解法.

2 解法探究

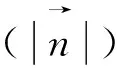
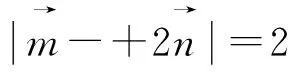
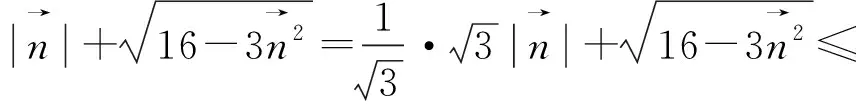
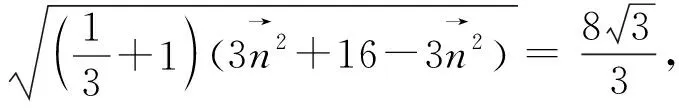
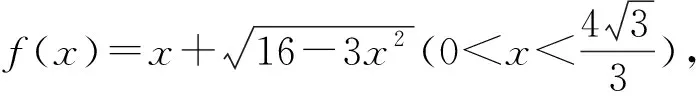
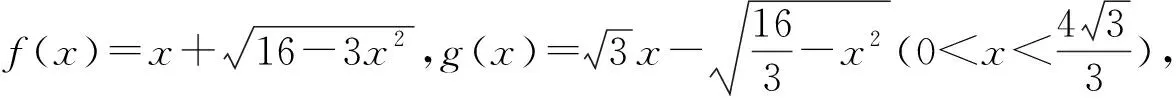
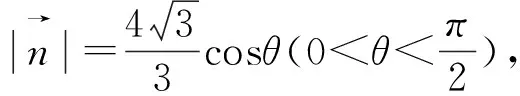
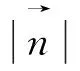
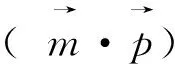
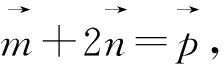
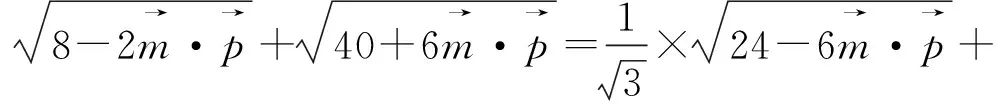
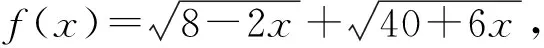
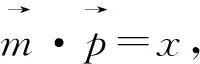
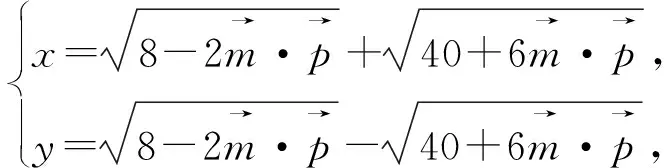
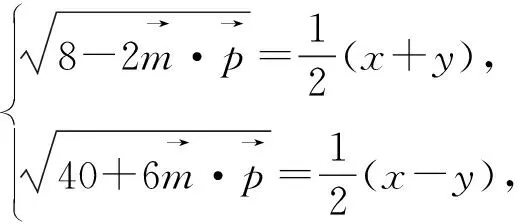
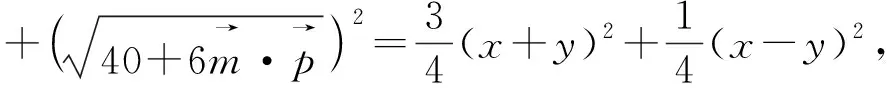
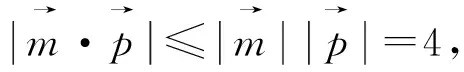
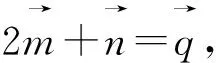
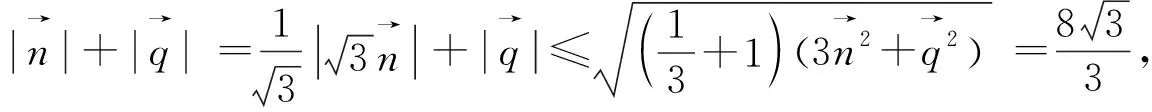
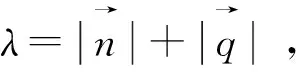
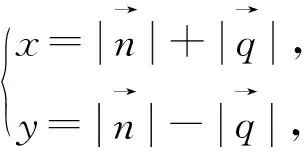
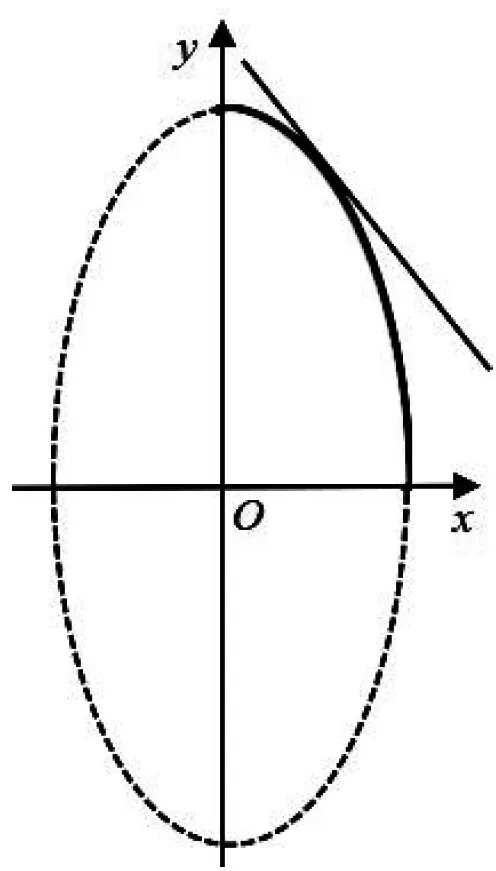
圖1

評注：除了對條件式換元，還可以從目標式入手，對目標式采用換元法，將問題轉化為二元二次方程(3x2+y2=16 (x,y>0))條件下的二元函數(x+y)最值問題 ，這里提供5種方法供讀者學習.

角度4：借助坐標，將問題轉化為二元二次方程( 圓方程)條件下的二元函數最值問題 .

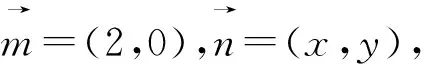
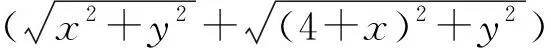
3 反思總結

從不同的角度出發思考問題，得到以上不同解法，思維方式的不同帶來解答形式的不同，給考生極大的思考與解答空間，在運算量和解答時間上出現差別，區分出不同層次的考生，具有很好的信度與區分度.一題多解不僅增加了問題涉及的知識廣度，而且以一帶多，可以減少考查同樣多知識的題量.在日常解題教學中，教師要善于通過解題發現知識間的內在聯系，體會知識間的轉化與化歸，構建知識間的網絡體系.這樣，學生在學習基礎知識，掌握基本技能的同時，可以有效鍛煉思維的深刻性、廣闊性、靈活性和創新性，達到舉一反三、融會貫通的解題水平和能力，但在日常的學習中，要結合自身掌握程度和實際情況，選擇最佳方法，不要一味追求某一種解法或過分追求一題多解，而是學會從不同解法中汲取不同的數學思想，從而提高自身的數學核心素養.