一種基于共生理論的工件加工可靠性方法研究

張欣欣，石秀敏，權利紅，祁宇明

（1.天津職業技術師范大學 機器人及智能裝備研究院，天津 300222；2.天津市智能機器人技術及應用企業重點實驗室，天津 300350；3.天津博諾智創機器人技術有限公司，天津 300350）

0 引言

隨著全球制造業的飛速發展，各行各業對機械生產的需求不斷提高，對機械加工零件的各項性能指標提出了更高的要求。然而在機械加工過程中，難免出現某些因素對工件的加工質量產生一定的影響，比如原材料質量的好壞以及設備的精度等。在工件加工過程中，要想確保工件的加工質量，就得有良好的加工設備，各設備之間良好的相互配合以及運轉是關鍵。工件的加工質量與主軸和刀具的配合程度就有很大關系，而主軸部件的運動精度和結構剛度是決定加工質量的重要因素，故對主軸提出了更高的要求。

基于共生關系去研究各種共生現象，常用的是Logistic 模型。經典的Logistic 模型是用來描述單一種群變化的，隨著研究的深入，一些學者對Logistic 模型進行了改進。例如，譚春輝等[1]將外部環境對產業造成的影響考慮到了最大產業容量中，對共生模型進行了改進；袁純清[2]將共生的概念引入研究小型經濟中，表示共生關系不止可以研究生物領域，也可以對之外的領域進行研究；周浩[3]對工業共生模型進行了Logistic模型分析，形成了一種動態的理論分析方法，對工件加工方面的研究具有一定的借鑒意義。基于共生理論對在加工過程中的主軸、刀具和工件之間的共生關系進行分析，將更加有利于提高工件的加工質量。

1 工件加工過程的共生條件分析

“共生”一詞來源于生物學中，在自然生態系統中，是指兩種或兩種以上的生物在長期的生活中形成緊密互利的生態關系。任何生物間的共生關系都不是單一存在的，它是相互促進，相互影響的，構成共生關系的三要素是共生單元、共生模式和共生環境[4]。

共生單元為共生體的構成奠定了基礎，共生單元是隨著分析主體的變化而變化的[4]。在機床加工工件過程中，共生單元主要是主軸、刀具以及工件等，本研究的是主軸、刀具以及工件的加工。

共生模式，是共生單元相互作用，相互聯合的方式，它能夠說明共生單元間相互影響的方式和和強度，也能反映共生單元間的信息交流和能量流動[5]。根據共生生態關系，工件加工過程的共生模式主要為競爭共生模式。

共生環境，是指除共生單元以外的所有要素的總和[5]，即機床主軸、刀具與工件所面臨的各種環境。

2 工件加工過程中Logistic 模型假設

假設1：將主軸與刀具視為一個主體，并把主體的不斷運行、不斷磨合看作是質參量的增加，記為T（t）。

假設2：在規定的時間和空間范圍內，隨著主軸與刀具的質參量增加，主軸與刀具之間的配合率也會增加，但到后期，主軸與刀具之間的配合率會不斷下降直至為零。所以假設面對不變的環境主軸與刀具之間的配合有一個臨界最大值，即為N，Nm 表示主軸與刀具的最大配合。

假設3：用r 表示主軸與刀具之間的振動頻率，主軸與刀具之間的振動頻率會因所處環境的不同而發生改變，所以一般r 也會不一樣。因此基本的Logistic模型為：

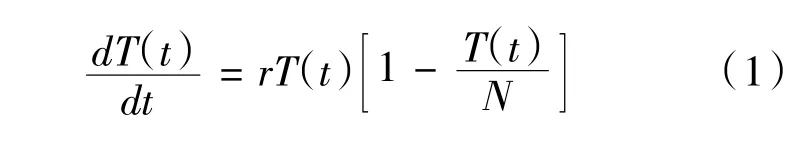
將主軸記為種群1，其他共生單元依次標記，T1（t）表示主軸的變化，其他共生單元主體的質參量表示為Tn（t）。

有一天，易非下夜班后回家，隔著防盜門，都聽見了小家里其樂融融的笑聲，她也受到了感染，不知不覺在臉上浮現出一朵微笑，可當她推門進去的時候，三人的笑聲都戛然而止，傳到半空中的笑聲都被他們吞了進去，大張著的嘴巴偽裝成一個個的呵欠，他們捂著嘴巴、伸著懶腰、站起來，關了電視，回到各自的房間里去了。

若主軸單獨存在，主軸的變化用logistic 模型表示為：

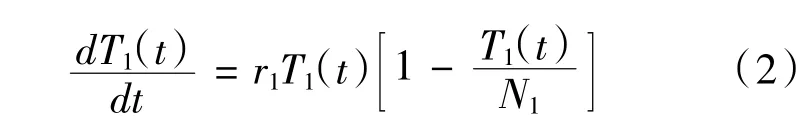
若其它共生單元單獨存在，其它共生單元運動變化用logistic 模型表示為：

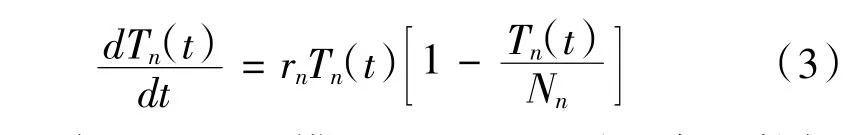
由此可知，Logistic 模型可以運用到機床工件加工過程中的。在此基礎上對主軸、刀具與工件的競爭共生關系進行Logistic 模型分析。

3 主軸、刀具與工件競爭共生模型及其穩定性分析

競爭模型是指雙方都受害的現象，具體表現是主軸與刀具的摩擦磨損，導致主軸與刀具的振動頻率發生變化以致于加工出來的工件孔精度偏低，圓柱度很差，主軸發熱很快，加工噪聲很大等問題。在競爭模式的狀態下，產生的是雙向能量流動。

假設在工件加工過程中，主軸、刀具與工件互為受害方，由于工件的加工需要主軸與刀具的相互作用，因此工件的加工對刀具以及主軸的配合狀況具有一定的抑制作用，而刀具和主軸之間振動的變化對工件的加工質量也有一定的抑制作用。

刀具、主軸以及工件之間的logistic 模型表現可以表示為：

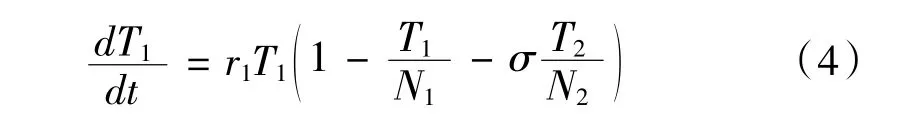
式中滓為刀具和主軸之間振動變化對工件加工質量的影響程度。

同時，工件的加工對刀具和主軸之間振動有一定的影響，這種變化可以表示為：

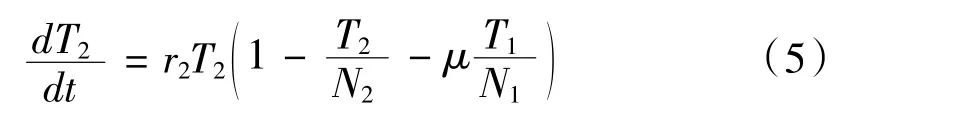
式中滋為工件加工對刀具和主軸配合狀況的影響。

在此共生系統中，該logistic 模型為：

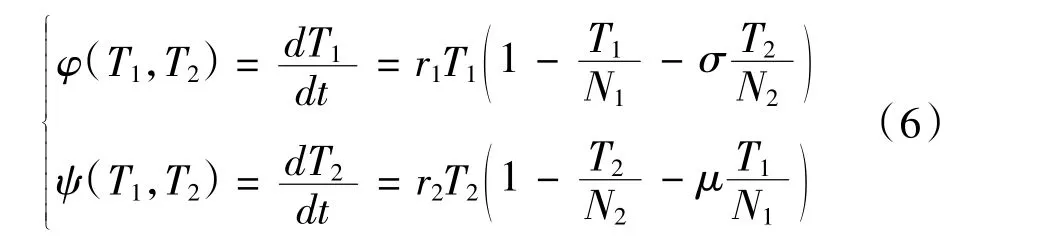
當達到共生的均衡狀態時的方程為：

對此方程組求解，得到共生模型的平衡點B1（0，0），當時滿足競爭條件。

對方程進行分析，將 漬（T1，T2），鬃（T1，T2）在B4點處進行Taylor 展開可得：

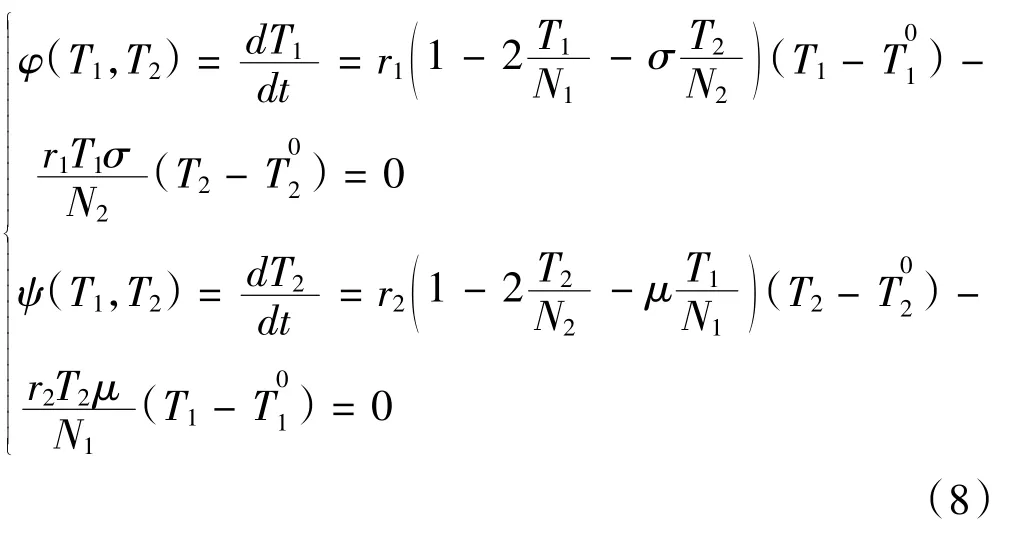
此方程的系數矩陣可記為

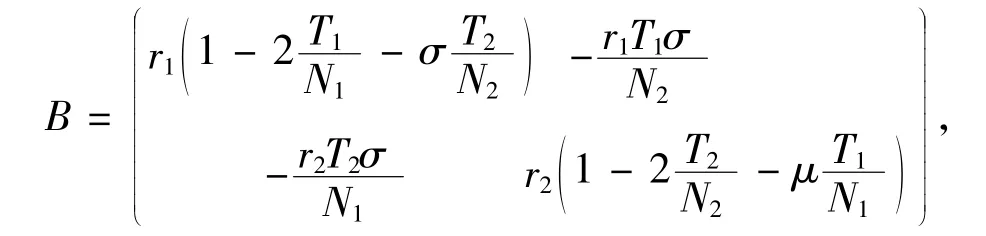
將B1（0，0），B2（N1，0），B3（0，N2），代入矩陣B 得

對B1：p = -（r1+ r2）< 0 q = r1r2> 0，共生系統不穩定，表明工件因為主軸與刀具的振動出現波動導致加工質量出現問題。

對B2：p = -r（21 - 滋）+ r1當且僅當 滋> 1 -時p > 0；q = -r1r2（1 - 滋）當且僅當 滋> 1 時q > 0；而p2逸4q 當且僅當1 > 滋> 0 時成立，矛盾，故不穩定。表明因為主軸與刀具磨損而出現振動波動導致工件精度不準確，加工質量下降等問題。

對B3：p = r2- r（11 - 滓）當且僅當 滓> 1 -時p > 0；q = -r1r2（1 - 滓）當且僅當 滓> 1 時q > 0；而因為{r2- r1（1 - 滓）}2+ 4r1r2（1 - 滓）> 0，所以p2逸4q此時共生系統穩定，說明主軸與刀具之間的配合狀況很好，主軸和刀具正常，沒有出現損傷，此時工件的質量可得到保證。

4 主軸、刀具與工件共生穩定性的仿真分析

在主軸、刀具與工件競爭共生模型中，假設T1代表的是刀具與主軸振動的變化，T2表示工件加工質量。以B4點為例，對主軸、刀具與工件的共生穩定性進行仿真分析，設置其他參數不變，改變競爭系數滓，滋的大小。對此設置兩組參數進行分析：

（a）r1= r2= 0.5；N1= N2= 500；滓 越0.3 滋 越0.5

（b）r1= r2= 0.5；N1= N2= 500；滓 越1 滋 越1.2

由圖（a）可以發現T1，T2兩條曲線隨著時間的變化不斷趨近，而圖1（b）兩條曲線隨著時間的變化越來越遠，由此可見當滓和滋小于1 時，隨著時間的變化，刀具與主軸的振動不斷趨于平穩，工件加工質量也達到穩定至最高處。而當滓和滋大于1 時，隨著時間的變化，刀具與主軸的振動不斷增大，而工件加工質量也不斷下降。

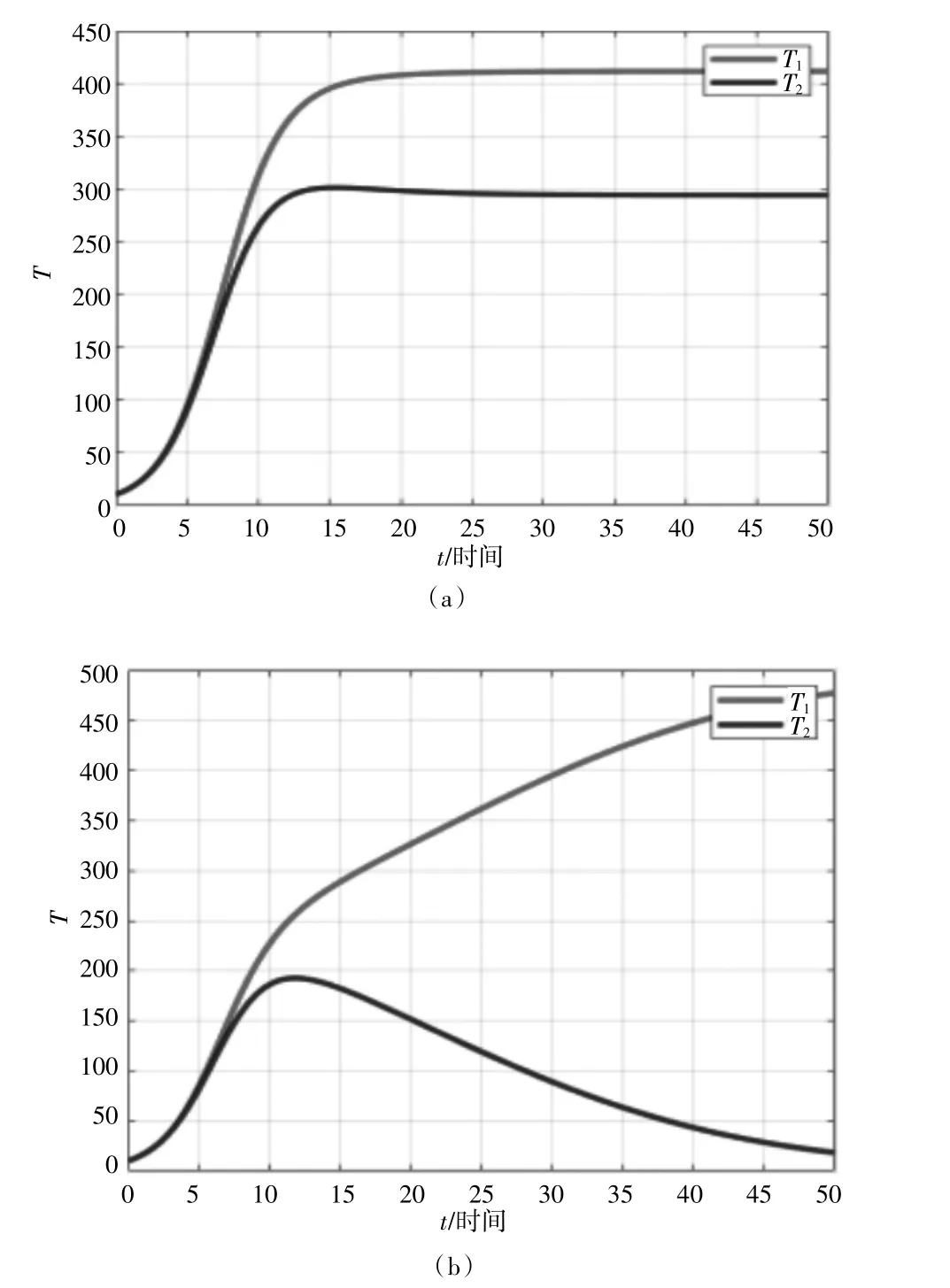
圖1 共生模型仿真

5 結語

基于生態理論構建了主軸、刀具和工件的競爭共生模型，分析了主軸、刀具和工件之間的共生條件，用Logistic 模型分析了主軸、刀具和工件的競爭共生穩定性。研究表明，當主軸、刀具與工件之間的影響程度較小時，共生系統可靠，主軸與刀具之間的配合狀況很好，主軸和刀具正常，沒有出現損傷，此時工件的質量可得到保證。當主軸、刀具與工件之間的影響程度較大時共生系統出現波動，將導致工件精度不準確，加工質量下降等問題。當機床在高速運轉時，研究工件加工質量與主軸和刀具配合狀況之間的關系提供了一種新的數學思路，可以更加具體，定性的評價工件的加工質量。

構建的假設條件有限，在工件加工過程中參與部件不僅僅是主軸和刀具，影響部件配合的因素更為復雜，這有待進一步研究。