利用習題改編提升解題能力
?重慶市江津中學校 周雪敏
部分教師無論是復習、單元測試還是模擬考試都習慣于搬用陳題來考核評價學生,這樣容易使學生陷入題海,又因題海并不切合學情,這樣不僅苦了學生又沒有達到預期的目標,事與愿違,可見,照搬陳題不適合提升學生的解題能力.為實現有針對性的復習和測試,教師可以對習題進行科學合理地改編,從而通過改編例習題讓學生鞏固雙基,通過改編錯題讓學生走出思維誤區,通過改編進行類比讓學生認清問題的本質,求同存異.這樣不僅可以避免學生飽受題海之苦,而且有助于學生思考問題、分析問題和解決問題能力的提升[1].
1 習題改編的原則
1.1 基礎性
教師在改編習題時切勿追求難、追求新,要重視鉆研教材,鉆研例習題,通過對基礎內容的改編來夯實學生的基礎知識和基本技能,這是教學的重中之重[2].
1.2 科學性
教師在改編習題時要做到條理清晰,結構合理,內容嚴謹.數學語言不能產生歧義,內容要符合學生的認知,題目要具有明確的指向性,決不能模棱兩可.習題只有具備科學性才會具有應用價值,不科學、不客觀的習題,不僅不能幫助學生鞏固知識,而且容易讓學生造成思維混亂,影響學生的進一步發展.
1.3 目的性
教師在改編題目前應制定明確的教學目標,并使題目的內容、形式、難度都按照這一目標進行改編,使題目更具針對性,更有助于學生的持續發展.
1.4 公平性
教師在改編題目時要尊重個體差異,根據本班學情編寫個性化的分層題目,為不同認知、不同水平的學生提供公平展示的舞臺,從而讓每個學生都有所提高.
2 習題改編的常用方法
2.1 陳題改編法
在談論數學學習能力時避免不了要談及數學解題能力,解題能力的培養離不開典型的陳題.若一味地練習陳題,不僅使學生陷入題海戰術,而且會因為學生對陳題的思考不夠,也無法發揮陳題的價值.因此,教師在教學中應通過對陳題的改編來繼續挖掘其價值,通過深入了解陳題來實現舉一反三、融會貫通的目的.
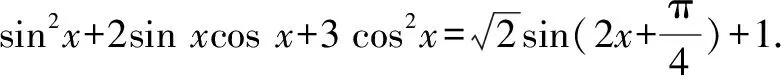
改編:已知函數y=sin2x+2sinxcosx+3cos2x-1,求函數的最小正周期.
改編后,由原來的倍半角公式的推理轉化為三角函數問題,更有利于考查學生綜合應用知識的能力.
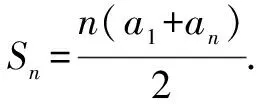
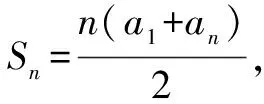
改編2已知數列{an}的前n項的和Sn=an2+bn+c,則滿足什么條件可使數列{an}是等差數列?
例2中推導出等差數列的前n項和的公式后,教師可利用改編1讓學生用逆向思維來思考等差數列.為了使問題更具開放性,教師又設計了改編2,讓學生思考等差數列前n項和公式成立的充要條件,從而達到對等差數列前n項和公式加深理解、靈活應用的目的.教學中,教師要善于通過小改動、小問題來激發學生探究的欲望,從而通過思考解決這些小變化來加深對原有知識的理解.
高考題目雖然變化莫測,但每個題目都有參考依據,這些依據的原型就是陳題,陳題對提升學生解題能力、夯實學生“雙基”發揮著舉足輕重的作用.陳題之所以“陳”是因為具有典型性,然而一直利用陳題不但不能引發學生再次對原題的思考,而且容易產生思維定式.因此,教學中可以通過對陳題的改編讓學生再一次回顧、反思、總結原題,這樣不僅鞏固了原題的思路,而且通過改編挖掘了原題的潛在價值,有利于鍛煉學生的理解能力、思維能力和創造能力.可見,陳題的改編對學生能力的培養發揮著不可估量的作用,教師通過改編讓學生引起對原題的聯想,逐漸培養學生對數學問題的研究意識,從而培養學生抓住問題本質提升數學解題的能力.
2.2 類比猜測法
在新知引入和舊知復習的過程中,教師要引導學生將結構相似、方法相似或關系相似等具有關聯的問題進行類比,運用聯想、歸納、總結、猜想等思維活動進行知識網絡的建構,從而培養學生綜合解決問題的能力.為了保障和檢驗類比猜測的有效實施,教師需要編制一些類比題目,讓學生經歷探究過程從而具備解一題會一類題的能力,這有利于培養學生的直覺思維能力,進一步提升數學應用能力.
例3設A(x1,y1),B(x2,y2)是拋物線y2=2px上的兩個動點(兩點不重合且異于頂點),且OA⊥OB(點O為原點),求證y1y2=4p2(為定值).
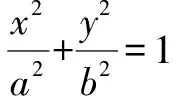
例3與例4結構相似,通過并列的類比讓學生將解拋物線問題的思路遷移至解橢圓的問題中,從而總結出證明此類問題的方法.類比遷移能力的培養也是一種自學能力的培養,通過引導學生對相似問題的猜想來激發學生探究的熱情,有助于提升學生分析問題和解決問題的能力.
2.3 逆推隱藏法
編寫題目時,教師應首先預設所要考查的內容,然后從確定的結論出發,一步步逆推,從而得出新題.此方法為題目編寫的常用方法,也是有效幫助學生查缺補漏的好方法.
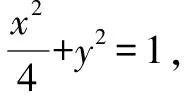
從本題的編寫過程可以看出,教師從確定的答案出發,結合所要考核的知識點,一步一步地逆推,目的明確,考點清晰.該方法常應用于日常教學中,教師從班級的學情出發,通過有針對性的題目幫助學生厘清思維障礙,有利于提升學生的解題能力.
2.4 延伸推廣法
編制數學題目時,教師可以通過擴大已知、延伸結論等方法對題目進行變式,從而讓學生在解題思路和解題方法的延伸中掌握解決問題的通性和通法,從而引導學生關注問題的本質,提升解題能力.
例5拋物線y2=2px(p>0)上有異于頂點O(0,0)的兩點A,B,若OA⊥OB,求證:直線AB過定點P(2p,0).
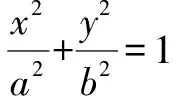
改編①讓學生從特殊中領悟一般規律,從而掌握解決問題的一般思路;改編②則充分利用了拋物線與橢圓的類比,引發學生對同類問題的思考.通過改編拓寬了學生思維的廣度,讓學生在解題的過程中不僅鞏固了知識,而且更加關注數學思想和數學方法的總結和歸納,有助于學生的發展.
3 對習題改編的思考
學生的認知是存在差異的,教學過程是動態變化的,這就使得在教學中可能會涌現出各種問題.如果對這些問題視而不見,按照原來預定的方法照本宣科,勢必會限制學生的發展.因此,這就要求教師在教學中要善于利用課堂的各種生成性資源,進行有效地引導和創造,從而幫助學生消除思維誤區,厘清知識的來龍去脈,幫助學生進行系統的知識建構,實現學生的全面發展.
總之,習題改編是每個教師都應具備的能力.教師必須認真鉆研教材、鉆研學生,從而設計出真正符合學生認知,適合學生發展的科學的、合理的題目,進而提升學生的解題能力,發展數學思維.

