周期性鋼彈簧浮置板軌道垂向振動帶隙特性研究

馮青松，戴承欣，郭文杰，付景文，楊 舟

（華東交通大學 鐵路環境振動與噪聲教育部工程研究中心，江西 南昌 330013）

隨著我國地鐵建設的蓬勃發展，新建地鐵線路不可避免地會下穿地表建筑［1］，為減弱地鐵運營過程中引起的環境振動對地表建筑及居民生活造成的不良影響，很多城市會在一些振動敏感地段鋪設鋼彈簧浮置板軌道。圖1為地鐵鋼彈簧浮置板軌道結構示意圖，圖中的“特征周期”為1 塊浮置板長度范圍內的軌道結構。由圖1可見，鋼彈簧浮置板軌道沿線路方向呈現明顯的周期性，故具有帶隙特性。在帶隙的頻率范圍內，彈性波無法沿結構傳播，從而使結構的振動明顯衰減。因此，研究周期性鋼彈簧浮置板軌道的帶隙特性，了解其內彈性波的傳播機理，對實現軌道結構的精細化減振具有重要的工程意義。

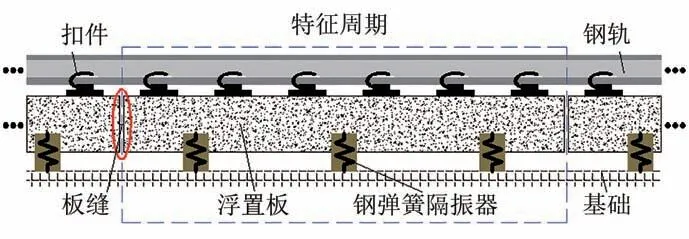
圖1 鋼彈簧浮置板軌道結構

關于周期性軌道結構，國內外學者很早就開展了相關研究。Grassie 等［2］將鐵路軌道結構考慮為周期離散支撐的梁，通過構建其廣義狀態矩陣，得到了軌道結構的導納函數。Nordborg等［3］通過分析周期支撐鋼軌的動力響應，發現“pinned-pinned”振動頻率的彈性波在鋼軌中的傳播不受抑制，且在較寬的振動衰減區內鋼軌的聲輻射處于極低水平。Thompson［4］針對周期性軌道結構，分析了其垂向導納和振動衰減率特性，并發現在與鋼軌波磨密切相關［5］的“pinned-pinned”頻率附近存在抑制彈性波傳播的禁帶。Sheng 等［6?8］提出用多梁模型或2.5 維波數有限元模型來求解周期支撐結構在諧荷載下的動力響應，并將該方法推廣到傳統有砟軌道中和板式無砟軌道中，得到了有砟軌道的振動傳播常數以及無砟軌道的振動和聲輻射特性。Wang 等［9?10］基于傳遞矩陣法和Bloch 理論求出了周期軌道結構的帶隙，發現布拉格帶隙和局部共振帶隙在周期軌道結構中共存，并以我國高速鐵路CRTS I 型雙塊式無砟軌道結構為研究對象，得到其頻散曲線。劉維寧等［11］將浮置板軌道簡化成周期性雙層歐拉梁模型，并基于廣義波數法求出了固定諧荷載下軌道結構的動力響應。易強等［12］結合傳遞矩陣法與Bloch 定理計算出了有砟軌道的帶隙，同時采用波疊加和功率流法分析了軌道結構的動力響應及軌道內彈性波的傳播特性。

然而，現有關于周期軌道結構研究主要集中在有砟軌道和高速鐵路無砟軌道領域，鮮有涉及城市軌道交通領域，尤其是地鐵鋼彈簧浮置板軌道。同時，現有研究中關于鋼彈簧浮置板軌道結構的模型相對簡化，通常是將其處理為梁-質量塊模型［13］、梁-梁模型［9，14］或梁-薄板模型［15］，若直接采用上述模型可能無法準確反映出浮置板軌道的帶隙特性。

目前常采用的周期結構帶隙計算方法是有限元法、傳遞矩陣法和平面波展開法。有限元法［16］通用性最高，但往往計算量大、耗時長，且不能進行機理分析；傳遞矩陣法［9?10，17］適用于求解簡單1 維結構帶隙，但無法對板這類二維結構進行建模；平面波展開法［18?19］適用于處理規則結構，但難以處理梁板耦合結構及板的邊界問題。此外，由于后2 種方法需要直接求解振動微分方程組，使得求解過程復雜，因而適用性不高。

本文以我國城市軌道交通中常用的鋼彈簧浮置板軌道結構為研究對象，基于能量變分原理求解其垂向振動帶隙，并采用有限元法驗證解析解的準確性。在此基礎上，分析鋼彈簧浮置板軌道各帶隙的形成機理，研究軌道結構剛度對帶隙的影響，并簡要說明帶隙理論在軌道結構精細化減振領域的應用思路。

1 基于能量變分原理求解鋼彈簧浮置板軌道帶隙

傳統的帶隙求解理論方法，如平面波展開法和傳遞矩陣法，在求解周期結構帶隙時主要是直接針對結構的振動微分方程組進行求解，對于多層組合或邊界條件復雜的結構，其微分方程的數量多，直接求解難度較大。能量變分原理具有將求微分方程邊值問題轉化為求泛函極值問題的優勢，適用于求解多層組合或邊界條件復雜的結構的帶隙問題。

基于能量變分原理求解鋼彈簧浮置板軌道帶隙的思路為：首先構建結構各組分的能量方程并求和得到結構的總能量方程，然后對總能量方程進行變分運算得到軌道結構振動的特征方程，最后對特征方程進行掃描波數求解獲得帶隙。

根據鋼彈簧浮置板軌道的結構特征，建立1 個特征周期的鋼彈簧浮置板軌道垂向振動分析模型，如圖2所示。圖中：d為浮置板長度；b為1/2浮置板寬；dg為板縫寬度；dr為扣件間距，且dr=（d+dg）/6；d+dg為特征周期長；yr和ys分別為鋼軌和鋼彈簧隔振器到浮置板外側自由邊界的距離；ORxR為1維的鋼軌坐標系；xOy為2維的浮置板坐標系。

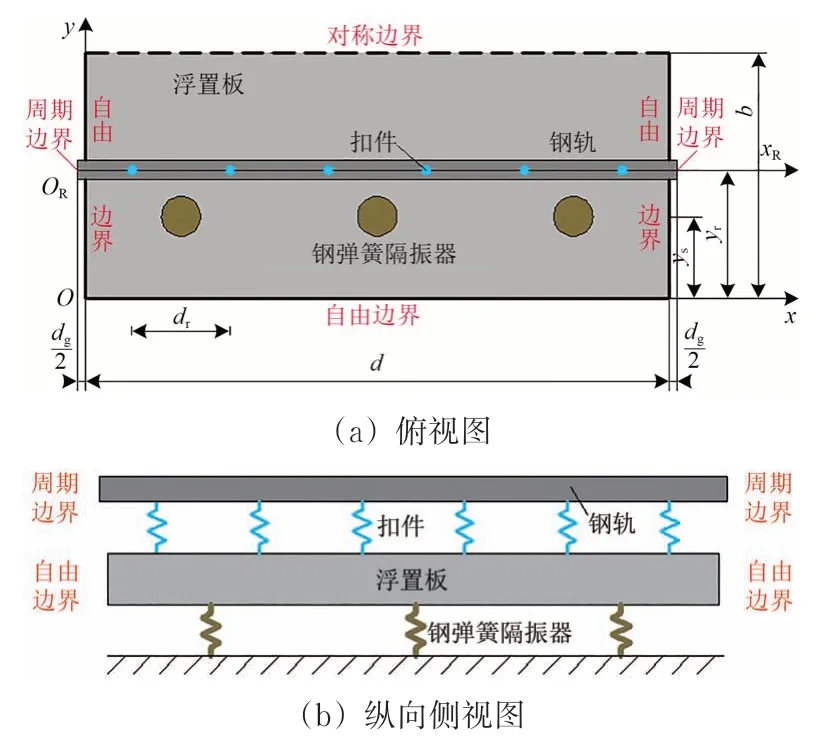
圖2 周期性鋼彈簧浮置板軌道垂向振動分析模型

分析中，將鋼軌視為鐵木辛柯梁，浮置板視為明德林中厚板，扣件與鋼彈簧隔振器均視為垂向支撐彈簧。已有研究結果顯示［20］，阻尼對軌道結構帶隙頻率影響不大，故本文不考慮阻尼的影響。

1.1 鋼彈簧浮置板軌道結構總能量

1.1.1 鋼軌能量

鋼軌能量包含彈性勢能和動能。分析軌道結構的垂向振動時，鋼軌位移只需考慮垂向位移和截面轉角位移。依據Bloch 理論和平面波級數[21]將鋼軌位移展開為

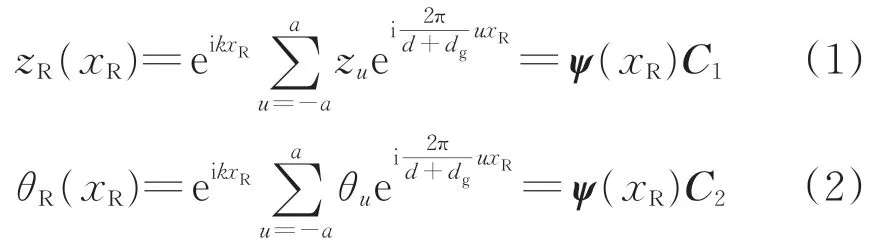
其中，

C1=(z?a z?a+1…z0…za?1za)T

C2=(θ?a θ?a+1…θ0…θa?1θa)T

式中：zR(xR)和θR(xR)（下文簡寫為zR和θR）分別為鋼軌的垂向位移和截面轉角位移；a為平面波級數截斷項數，本文取a=20；k為波數；xR為鋼軌的橫坐標；ψ(xR)為關于xR的試函數行向量；zu和θu均為未知系數。

根據鐵木辛柯梁理論［26］，可得到鋼軌彈性勢能UR為

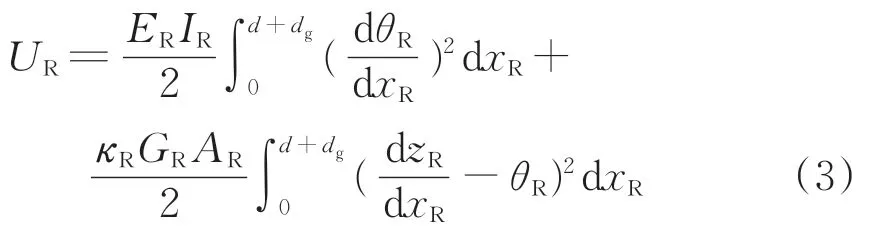
式中：ER，IR，κR，GR和AR分別為鋼軌的彈性模量、截面慣性矩、截面剪切系數、剪切模量和截面積。

將式（1）和式（2）代入式（3）得

其中，

C=(C1C2)T

式中：KR為鋼軌的剛度矩陣。

鋼軌動能VR可表示為

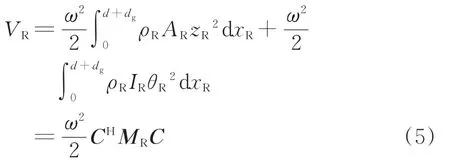
式中：ω為軌道結構特征圓頻率；ρR為鋼軌的密度；MR為鋼軌的質量矩陣。

1.1.2 浮置板能量

浮置板能量包含彈性勢能和動能。分析浮置板的垂向振動特性時，需要考慮剪切變形和轉動慣量的影響。考慮垂向位移、x和y方向的轉角位移，采用改進傅里葉級數[22]分別將其表示為

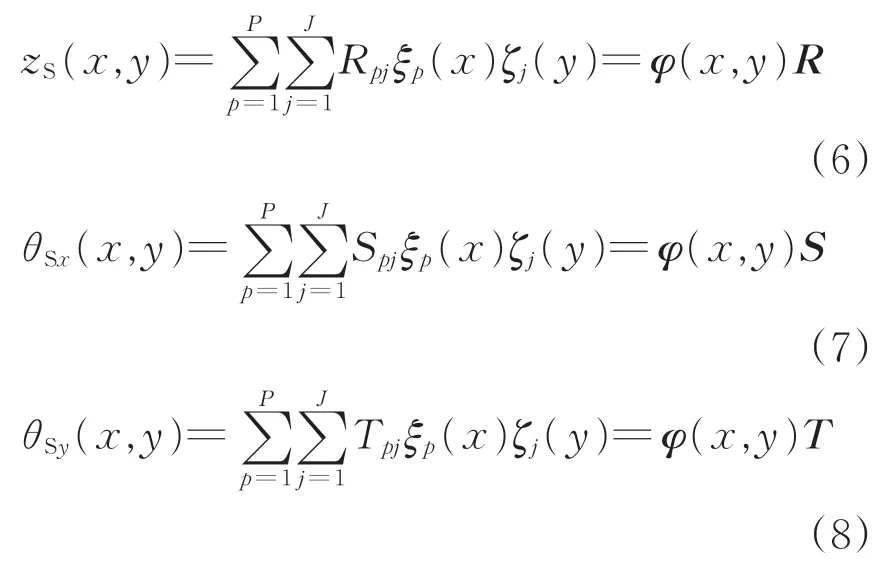
其中，

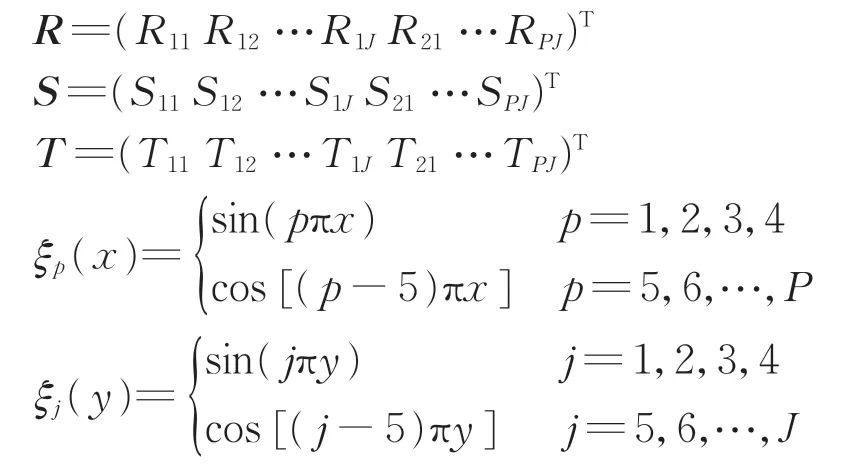
式中：zS（x，y），θSx（x，y）和θSy（x，y）（下文簡寫為zS，θSx和θSy）分別為浮置板的垂向位移以及浮置板在x方向和y方向的轉角；Rpj，Spj和Tpj均為未知系數；φ（x，y）為浮置板位移的試函數行向量；ξp（x）和ζj（y）為具有任意性的改進傅里葉級數；P和J分別為x和y方向的改進傅里葉級數截斷項數，本文取P=J=14。

根據明德林板理論［27］，浮置板的彈性勢能Us和動能Vs分別表示為

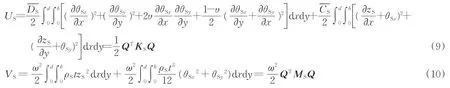
其中，

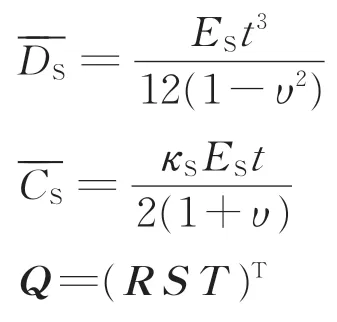
本文模型中，浮置板存在對稱邊界和自由邊界2 種邊界。根據譜幾何法[23?25]，需用人工彈簧模擬浮置板的邊界條件。在圖2的xOy坐標系中，y=b是浮置板的對稱邊界，此處的角位移θSy=0而垂向線位移自由，故取轉角彈簧剛度kθSy=∞N·rad?1和平動彈簧剛度kSz=0 N·m?2；而浮置板的其他3 個側面為自由邊界，故取kθSy=0 N·rad?1和kSz=0 N·m?2。

因此，浮置板的邊界勢能UB可表示為

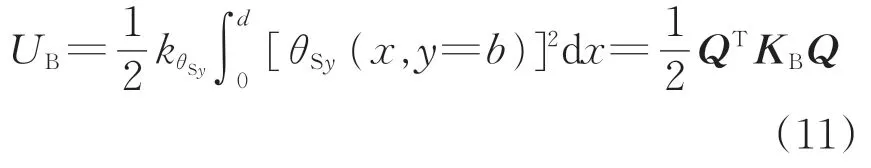
式中：kθSy為均布轉角彈簧剛度；KB為邊界彈簧剛度矩陣。

1.1.3 扣件彈性勢能

扣件變形量等于鋼軌與浮置板垂向位移之差

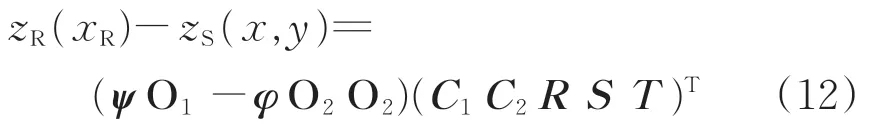
扣件的彈性勢能UF為

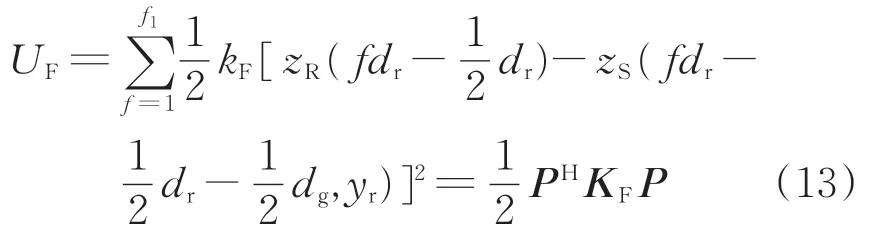
其中，

P=（C1C2R S T）T

式中：O1是（2a+1）維元素為零的行向量；O2是PJ維元素為零的行向量；kF是扣件的垂向剛度；f1是1個計算周期內扣件的個數；KF是扣件系統的剛度矩陣。

1.1.4 鋼彈簧隔振器彈性勢能

鋼彈簧隔振器的彈性勢能Uss可表示為

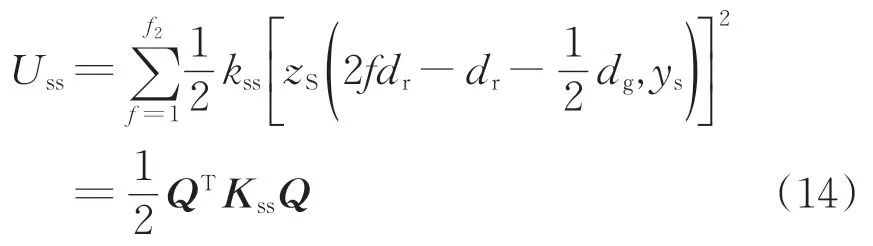
式中：kss為鋼彈簧支撐剛度；f2為1 個特征周期內鋼彈簧的個數；Kss為鋼彈簧剛度矩陣。

1.1.5 結構總能量

鋼彈簧浮置板軌道結構的總能量Π等于其總彈性勢能與總動能之差，即

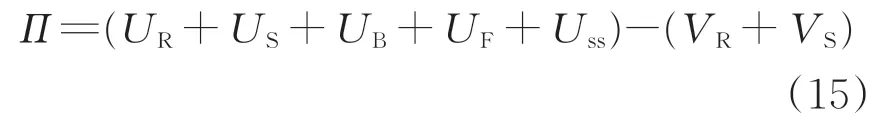
1.2 鋼彈簧浮置板軌道結構特征方程和帶隙求解

依據Hamilton 原理，對總能量Π進行1 次變分［28］得到變分方程δΠ，然后對總能量Π求極值有

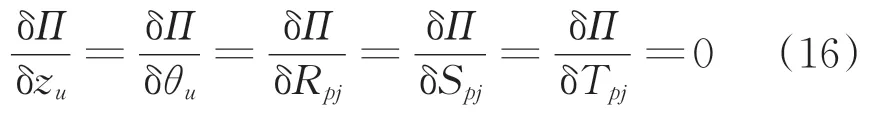
聯立式（15）和式（16），得到鋼彈簧浮置板軌道結構特征方程

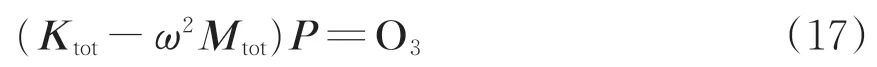
式中：Ktot和Mtot分別是軌道結構的總剛度矩陣和總質量矩陣；O3是（4a+2+3PJ）×1的零矩陣。

通過對總能量泛函求極值，軌道結構垂向振動問題的求解被轉化成了其特征頻率的求解。然后，在第一Brillioun 區范圍內，對式（17）進行掃描波數求解即可得到周期鋼彈簧浮置板軌道的頻散曲線，進而得到帶隙。

2 有限元驗證

運用多物理場耦合分析軟件COMSOL Multi?physics 建立周期性鋼彈簧浮置板軌道的有限元模型。由于軌道結構具有對稱性，取一半結構進行建模：鋼軌和浮置板均為實體單元，扣件和鋼彈簧隔振器分別采用彈性薄層單元和彈簧基礎單元模擬；浮置板的內側設置為對稱邊界，其余各邊均為自由邊界，鋼軌2 端設置為Floquet 周期邊界；單元類型設置為Langrage-Quadrastic；如圖3所示，選用固體力學模塊進行求解。

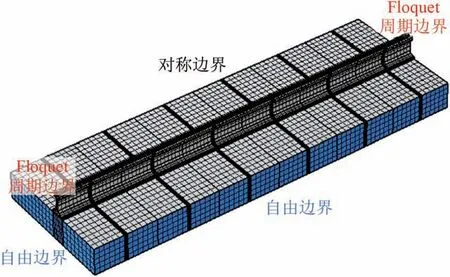
圖3 周期性鋼彈簧浮置板軌道有限元模型

浮置板選用我國城市軌道交通常用的預制3.6 m 短板，其板長3.57 m，寬3 m，厚0.3 m，板縫0.03 m。其他相關軌道參數［14］見表1。

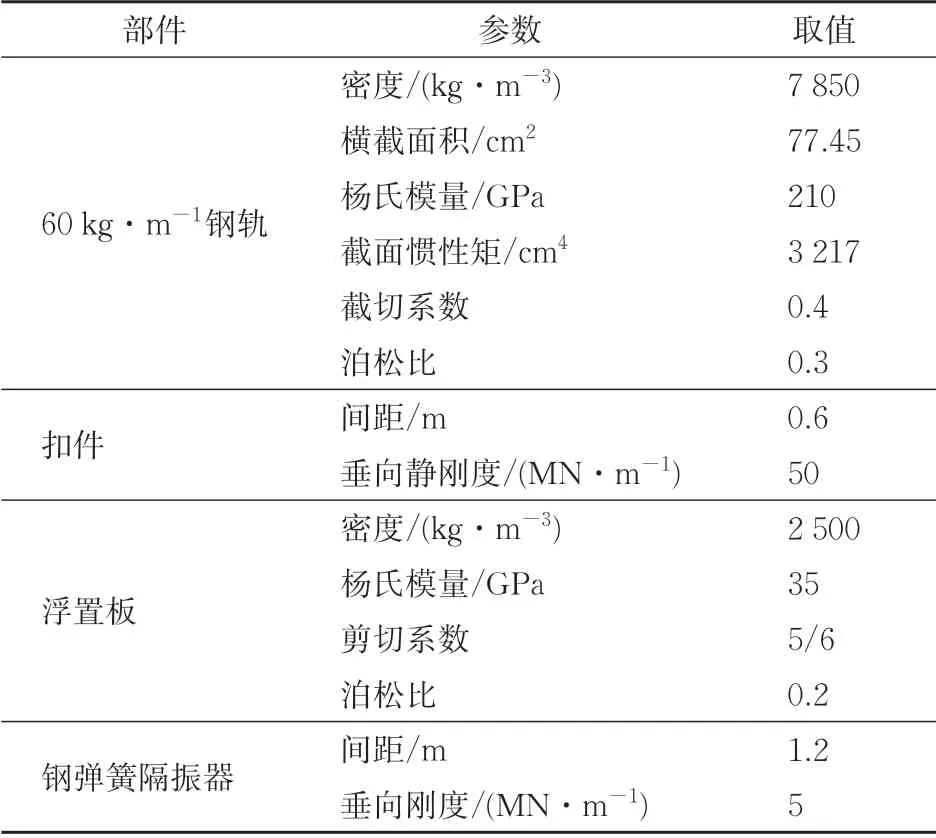
表1 預制3.6 m短板浮置板軌道計算參數

為便于繪圖，此處引入簡約波矢α，其與波矢k之間的關系為α=k（d+dg）/π。對于鋼彈簧浮置板軌道這種1 維周期性結構，在第一Brillioun 區內，波矢k?［?π/（d+dg），π/（d+dg）］［19］，故α∈［?1，1］。這樣，可得到關于頻率與簡約波矢α的頻散關系。此外，現有研究表明［7，9?10］，軌道結構中1 000 Hz 以上的垂向振動帶隙均是鋼軌“pinned-pinned”振動模式所引起，為簡化分析過程，本文只研究至第1階“pinned-pinned”頻率（本文為1 082.0 Hz）處的帶隙，因此分析了0～1 200 Hz 范圍內帶隙。為適當減少帶隙數量以降低分析的工作量，本文忽略了帶寬不足5 Hz 且相對帶寬（相對帶寬=帶寬/帶寬中心頻率×100%）不足5%的帶隙。

圖4和圖5分別為解析方法和有限元方法求得的軌道結構低頻帶隙圖和高頻帶隙圖，圖中灰色部分為帶隙。由圖可知：解析解和有限元解均表明在0～1 200 Hz 范圍內周期鋼彈簧浮置板軌道結構共存在5 條垂向振動帶隙。將二者帶隙頻率計算結果列表對比，見表2。

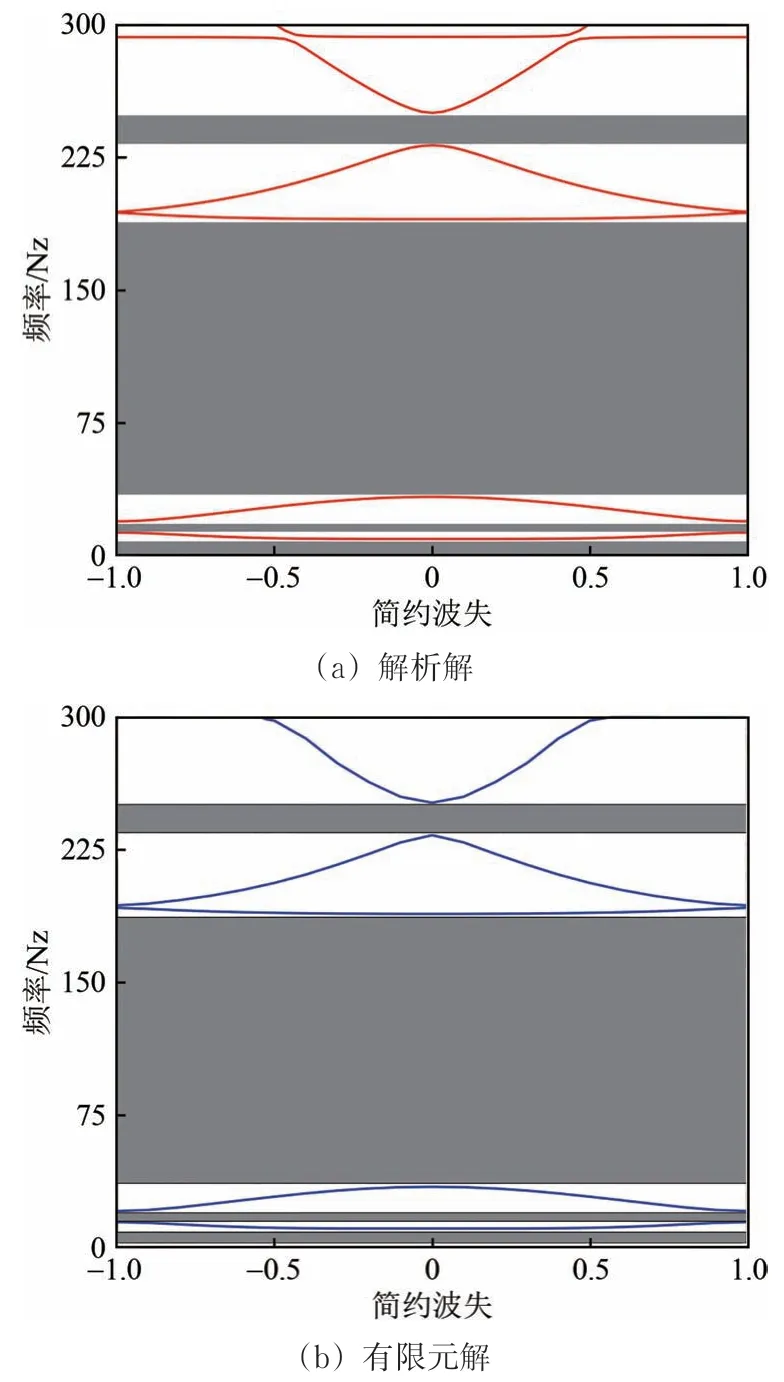
圖4 低頻帶隙對比

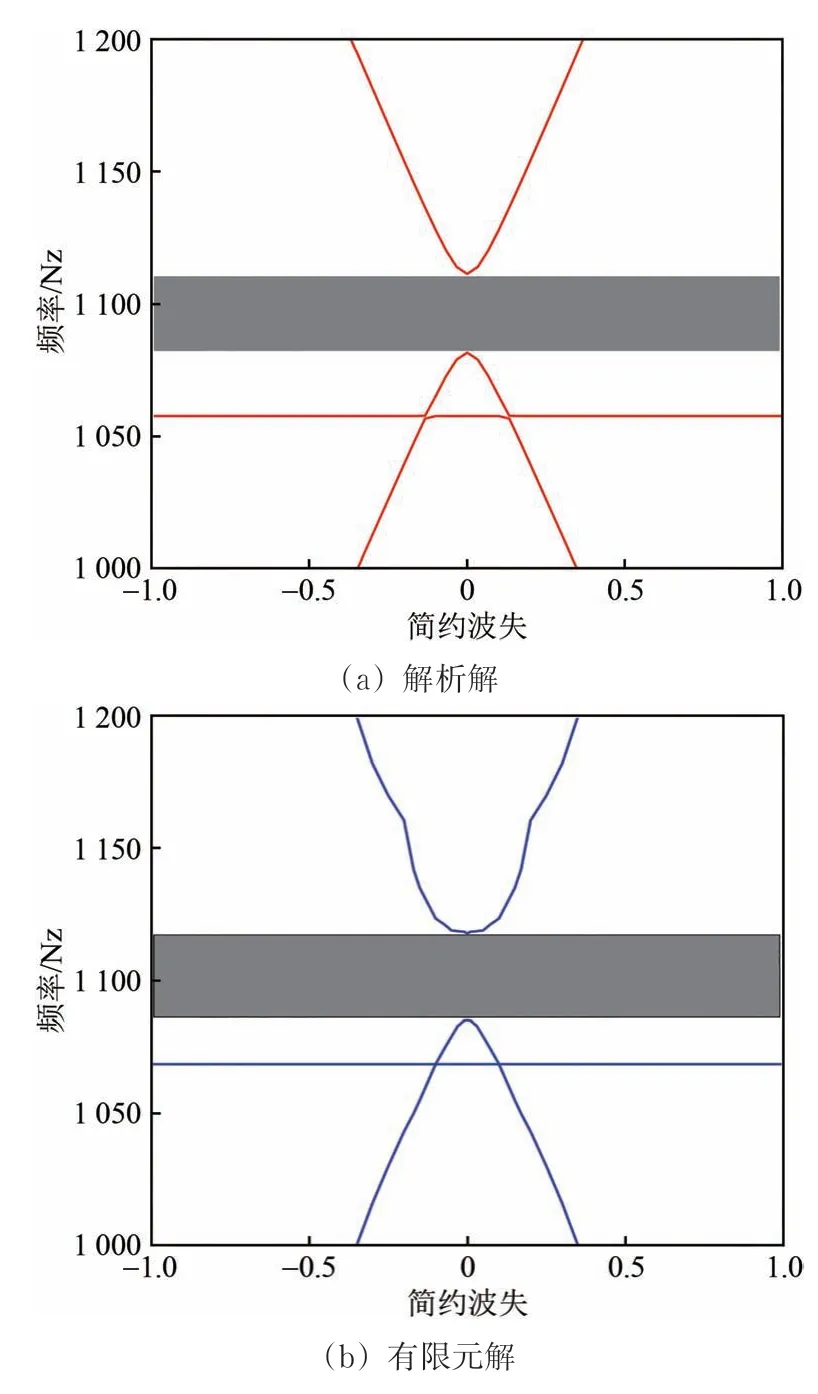
圖5 高頻帶隙對比

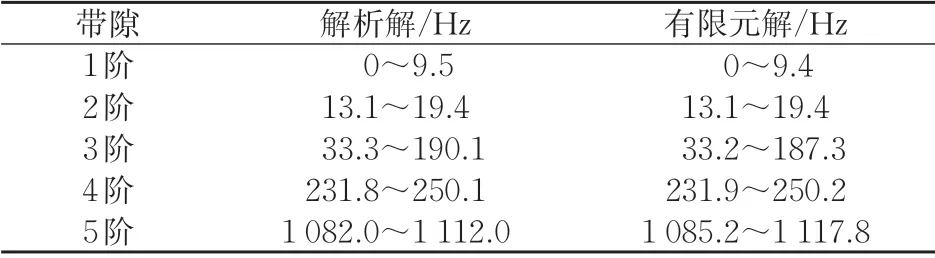
表2 0～1 200 Hz范圍內各垂向振動帶隙頻率對比

由圖4、圖5和表2可知：解析解與有限元解吻合程度較高，帶隙圖以及各階帶隙的頻率位置也基本一致，從而證明了解析方法的正確性；在0～1 200 Hz 范圍內，鐵木辛柯梁-明德林板耦合模型可準確地反映周期鋼彈簧浮置板軌道的垂向振動帶隙特性。

在配置為i5-10400CPU/16G 運存/2.9 GHz 主頻的計算機上，有限元仿真的計算時間為1 287 s，而解析求解僅需6 s，計算效率是前者的215 倍。因此，本文解析方法不僅精確，而且計算效率高，有利于進行參數化分析。

3 帶隙形成機理

由上述研究可知，在0～1 200 Hz 范圍內，周期性鋼彈簧浮置板軌道共存在5 條垂向振動帶隙，但尚不清楚其形成機理。為深入了解鋼彈簧浮置板軌道結構中彈性波的傳播特性，本節將從機理上對各帶隙形成機理進行分析。

軌道結構局域共振帶隙的形成主要受到特征周期內軌道結構自振特性和鋼軌中彎曲波相互作用的影響。根據浮置板軌道的結構特性，其局域共振帶隙起始和截止頻率可分別采用“彈簧-質量-彈簧-質量”模型和“質量-彈簧-質量-彈簧”模型［9，17，29?30］來估算，如圖6所示。

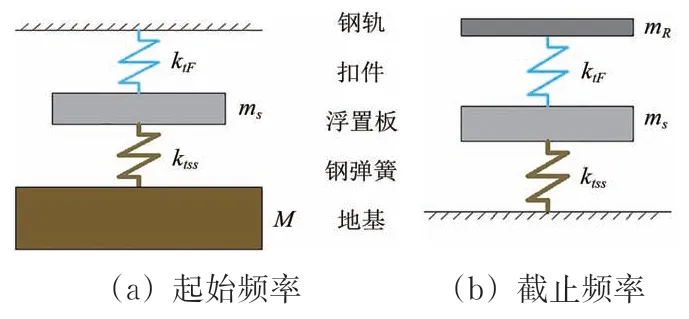
圖6 鋼彈簧浮置板軌道局域共振帶隙估算模型

由圖6可推出局域共振帶隙的起始頻率fl1，fl2和截止頻率fu1，fu2分別為［30］

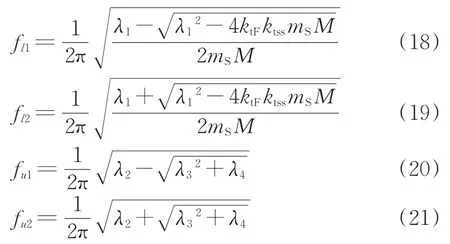
其中，

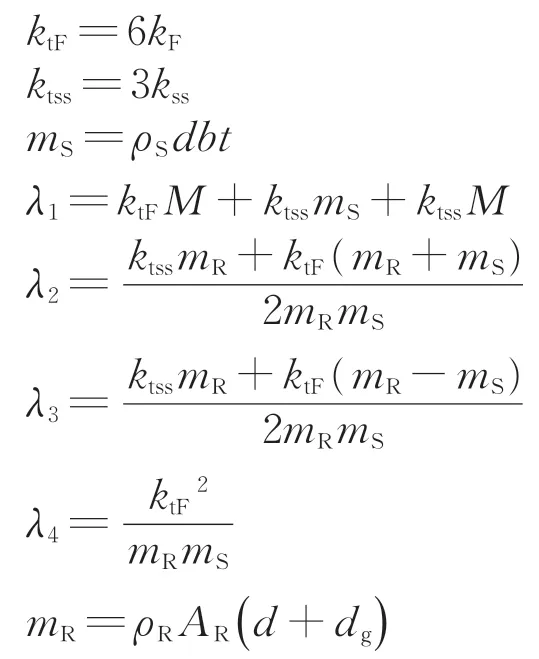
式中：ktF和ktss分別是1個特征周期內扣件和鋼彈簧的總支撐剛度；mR和mS分別是1 個特征周期內鋼軌和軌道板的質量；M為地基質量，取M=∞。

將表1中鋼軌和浮置板的質量及扣件和鋼彈簧的剛度代入式（18）—式（21），解得fl1=0 Hz，fl2=44.6 Hz，fu1=9.5 Hz，fu2=191.4 Hz，即局域共振帶隙的估算結果為：0～9.5 Hz，44.6～191.4 Hz。該結果與解析解和有限元解的1 階與3 階帶隙基本吻合，從而可以說明周期性鋼彈簧浮置板軌道的1 階和3 階帶隙為局域共振帶隙，同時也從側面驗證了解析方法的準確性。

根據已有研究［9—10］，對于周期性鋼彈簧浮置板軌道結構，在第1 階局域共振帶隙的起始頻率處，鋼軌和浮置板為靜止狀態，地基做方向向下的剛性運動，這表明0～9.5 Hz 范圍內的彈性波無法沿鋼軌縱向傳播，而是沿著扣件-軌道板-鋼彈簧直接向下傳入地基中，從而引起周圍土體振動，因此浮置板軌道難以隔離極低頻率的彈性波；在第2 階局域共振帶隙的起始頻率處，鋼軌和地基為靜止狀態，軌道板做方向向下的剛性運動，這表明33.3～190.1 Hz 范圍內的彈性波無法沿鋼軌縱向傳播，而是被限制在激振點附近的浮置板內，從而引起浮置板振動。

布拉格帶隙一般位于軌道結構的n階“pinnedpinned”頻率處，且首階“pinned-pinned”頻率對應于首階布拉格帶隙的起始頻率［9—10］。根據文獻［7］，當鋼軌中彎曲波的頻率達到第1 階“pinnedpinned”共振頻率時，取1 跨鋼軌研究，其振型為正對稱形式，且在跨中的垂向位移最大，扣件連接處位移最小，如圖7所示，圖中實體部分為初始狀態，虛線部分為振型。

圖7 1跨鋼軌第1階“pinned-pinned”振型

對于有限長結構，其位移可用改進傅里葉級數構造，因此圖7中鋼軌的垂向位移和轉角位移可寫為

式中：R1和R2為待定系數且不同時為零。

結合鋼軌的自由振動微分方程，則軌道結構“pinned-pinned”頻率應滿足

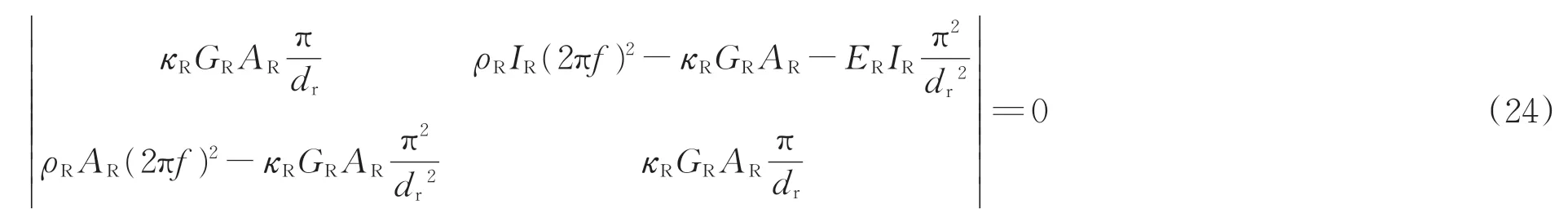
將鋼軌和扣件參數帶入式（24），解得第1 階“pinned-pinned”頻率為1 081.9 Hz。該值與5階帶隙的起始頻率1 082 Hz基本一致，這表明周期性鋼彈簧浮置板軌道的5 階帶隙是布拉格帶隙。同時，從式（24）還可看出布拉格帶隙起始頻率僅與鋼軌的物理特性和扣件間距有關。根據布拉格散射機理［31］，彈性波在最小周期處（扣件處）會發生反射，再和原來的波發生抵消，進而形成帶隙。

2 階和4 階帶隙則是由軌道結構的彈性運動產生。圖8為2 階帶隙起始和截止頻率處的鋼彈簧浮置板軌道振型。由圖可知：在2 階帶隙的起始和截止頻率處，鋼軌做彈性運動，浮置板做剛性運動，這意味著彈性波自鋼軌傳入浮置板后會引起浮置板做剛性運動，二者的聯合運動會耗散彈性波大量的能量從而形成帶隙。

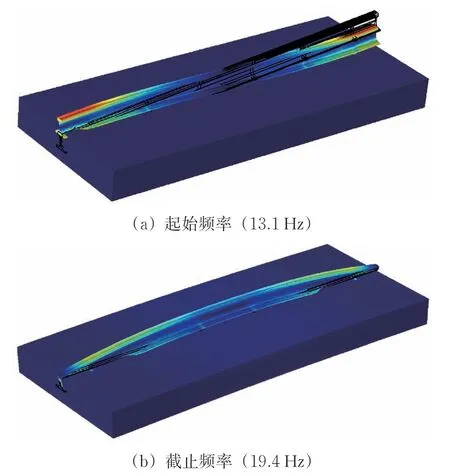
圖8 2階帶隙起始與截止頻率所對應的振型

圖9為4 階帶隙起始和截止頻率處的鋼彈簧浮置板軌道振型。由圖可知：在4 階帶隙的起始和截止頻率處，鋼軌做彈性運動，浮置板也做彈性運動，這意味著彈性波自鋼軌傳入浮置板后會引起浮置板做彈性運動，二者的聯合彈性運動會耗散彈性波大量的能量從而形成帶隙。

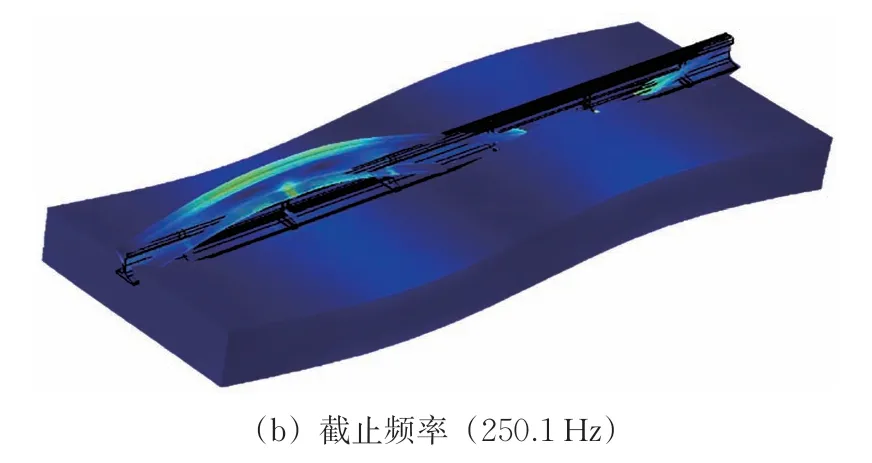
圖9 4階帶隙起始與截止頻率所對應的振型

4 軌道結構剛度對帶隙的影響

在實際工程中，軌道結構剛度是最容易調節的。因此，本節分別從扣件剛度和鋼彈簧剛度2 方面考慮其對浮置板軌道垂向振動帶隙的影響。

4.1 扣件剛度對帶隙的影響

分別將扣件垂向靜剛度設為30，40，50，60和70 MN·m?1，其余參數不變進行帶隙求解，得到不同扣件剛度下浮置板軌道各階帶隙，如圖10所示。當扣件剛度為50 MN·m?1時，浮置板的彈性運動會和結構的剛體運動發生耦合，從而在通帶范圍內產生1 條禁帶，即4 階帶隙，而當扣件剛度處于其他范圍時4階帶隙寬度不足5 Hz，即無明顯的4 階帶隙，故下面就不繪制4 階帶隙頻率隨扣件剛度的變化圖。

由圖10可知：當扣件剛度為30～70 MN·m?1時，1 階帶隙不受扣件剛度變化的影響，2 階和3 階帶隙的起、止頻率均隨扣件剛度的增加而增加，且截止頻率增速更大，2階帶寬由4.7 Hz增至7.6 Hz，增幅64%，3 階帶寬由119.8 Hz 增至187.2 Hz，增幅56%；5 階帶隙的起始頻率不受扣件剛度的影響，截止頻率則增加明顯，帶寬由18 Hz 增至41 Hz，增大1.3 倍。綜上，扣件剛度對2 階帶隙、3 階帶隙和4 階帶隙影響顯著，且隨著扣件剛度增大，其帶寬與截止頻率將明顯增大。

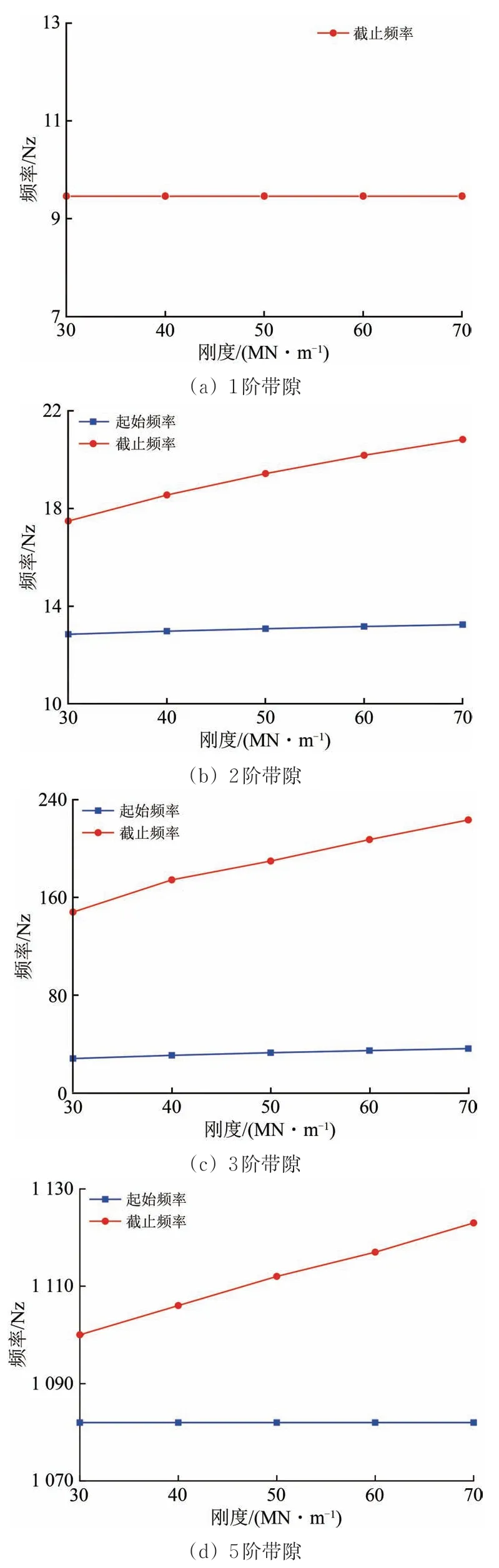
圖10 扣件剛度對帶隙的影響

4.2 鋼彈簧剛度對帶隙的影響

將鋼彈簧剛度分別設為3，4，5，6和7MN·m?1，得到不同鋼彈簧剛度下浮置板軌道帶隙，如圖11所示。

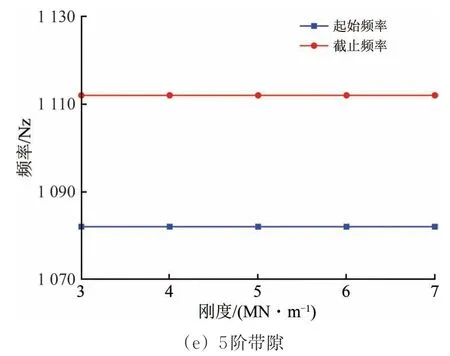
圖11 鋼彈簧剛度對帶隙的影響

由圖11可知：當鋼彈簧剛度為3～7 MN·m?1時，隨著鋼彈簧剛度的增加，1 階帶隙變化明顯，其截止頻率增長迅速，帶寬由7.3 Hz 增至11.2 Hz，增幅53%；2階帶隙頻率略往上移，但帶寬總體上保持不變；3、4和5階帶隙基本不受鋼彈簧剛度的影響。因此，鋼彈簧剛度主要影響1 階帶隙，且隨著鋼彈簧剛度增大，其帶寬與截止將明顯增大。

5 帶隙理論的工程應用

對鐵路軌道這類層狀結構，準確研判其內部彈性波傳播的頻率范圍及傳播路徑是很重要的，這可為未來實現整體結構的精細化減振提供理論依據。因此，本節將鋼彈簧浮置板軌道和普通整體道床軌道的帶隙特性進行對比分析，以從帶隙角度解釋鋼彈簧浮置板軌道的隔振性能，并簡要說明帶隙理論在軌道結構精細化減振領域的潛力。

在城市軌道交通中，整體道床通常是直接澆筑在隧道仰拱或高架橋面上，下部基礎剛度很大，即普通整體道床軌道可簡化為周期離散支撐鋼軌［20］，其帶隙如圖12所示。

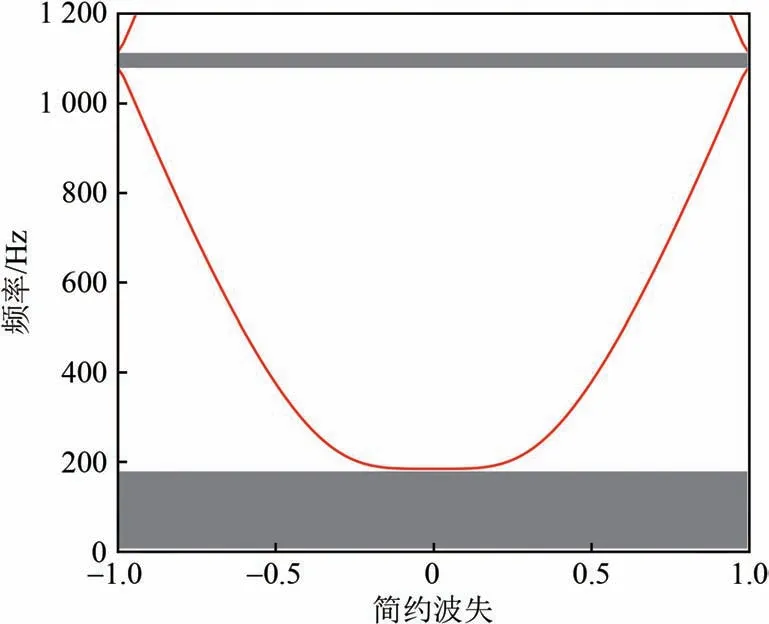
圖12 普通整體道床軌道帶隙

由圖12可知：在0～1 200 Hz 范圍內，普通整體道床軌道垂向振動僅有0～185.2 Hz和1 082.0～1 112.0 Hz 的2 條帶隙，第1 階為局域共振帶隙，該帶隙內彈性波無法沿軌道傳播，并直接向下傳入地基中，第2 階為布拉格帶隙，彈性波在最小周期邊界處發生干涉相消。表3將普通整體道床和浮置板2種軌道結構垂向振動帶隙對比結果見表3。

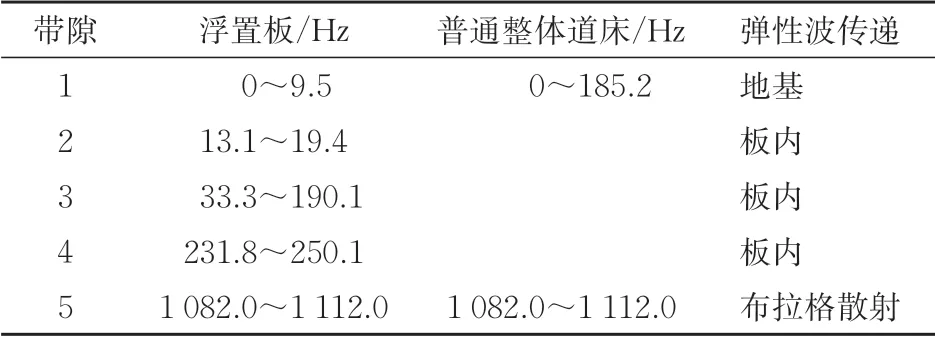
表3 0～1 200 Hz內2類軌道結構中彈性波傳播情況

由表3可知：在低頻帶隙內，普通整體道床軌道中彈性波將全部傳入下部基礎，而浮置板軌道僅有很少一部分彈性波會傳入地基，其余帶隙內的彈性波將全部被限制在板內，這說明浮置板軌道隔振性能明顯優于普通整體道床軌道。

通過上述分析，可針對性地對浮置板軌道結構中的彈性波進行控制：在1階帶隙范圍內，彈性波主要傳入地基土體中并引起環境振動，故應以0～9.5 Hz作為基準，在土體中增置排溝［32］、周期性隔振墻或排樁［33］進行治理；在2～4階帶隙范圍內，彈性波主要傳入浮置板中并引起浮置板振動，故可在板上分別設置中心頻率為16.25，111.70和240.95 Hz的動力吸振器［34］以減小其振動；在通帶范圍內，彈性波主要在鋼軌中傳播并引起鋼軌振動，故可以其他頻率為基準設置吸振器并可在鋼軌上附加阻尼，如設計為阻尼鋼軌［35］減振。

6 結 論

（1）采用鐵木辛柯梁-明德林板耦合模型，基于能量變分原理求解周期性鋼彈簧浮置板軌道垂向振動帶隙是準確可靠的，與有限元法相比，該方法計算效率更高。

（2）在0～1 200 Hz 范圍內，周期性鋼彈簧浮置板軌道結構中存在5 條帶隙，其對應頻率范圍為0～9.5，13.1～19.4，33.3～190.1，231.8～250.1和1 082.0～1 112.0 Hz。其中：第1 和第3 階為局域共振帶隙；第5 階為布拉格帶隙；第2 階和第4階帶隙是由軌道結構的彈性運動所引起。

（3）在1 階帶隙內，彈性波自鋼軌直接傳入地基中，且帶隙寬度隨鋼彈簧剛度增大而增大；在2～4 階帶隙中，彈性波因局域共振和軌道的彈性運動而被限制在激振點附近的浮置板中，其帶隙的頻率位置及寬度主要受到扣件剛度影響；在5 階帶隙內，彈性波則因布拉格散射而被耗散了，帶隙寬度與扣件剛度成正相關。

（4）本研究有助于準確掌握周期性鋼彈簧軌道結構中彈性波傳播的頻率范圍及路徑，為將來實現整體結構的精細化減振提供必要的理論依據。針對1 階帶隙中的彈性波，宜以0～9.5 Hz 為基準設計減隔振基礎；針對2～4 帶隙中的彈性波，宜以設計中心頻率為16.25，111.70 和240.95 Hz 的浮置板吸振器；其他頻率段的彈性波可根據實際需求針對性設計鋼軌吸振器。