低溫下泡沫混凝土的動態力學性能

吳森寶，宗 琦，王軍國，汪海波，王夢想，賈 虎

(1.安徽理工大學土木建筑學院，淮南 232001；2.南陽師范學院土木建筑工程學院，南陽 200125)

0 引 言

當前，我國提倡建筑節能，綠色環保。在建筑工程中，泡沫混凝土的建筑成本比普通混凝土要便宜48%，二氧化碳排放量也相對減少48%[1]，且泡沫混凝土還具有輕質、隔熱性能與隔音性能好、低彈抗震[2]等優點，這些優點使其成為建筑節能的首選材料。目前大多數研究主要針對泡沫混凝土的物理性能與靜態性能，Kearsley等[3]研究了泡沫混凝土在不同孔隙率下的抗壓強度，并求出了二者之間的函數關系；為了提高泡沫混凝土的力學性能，一些研究者們在泡沫混凝土中加入添加劑，如納米改性沙[4]、粉煤灰[5]、混合纖維[6]等，此外添加劑的含量[7-8]也對泡沫混凝土的性能有一定影響;還有部分研究者關注發泡劑[9]對泡沫混凝土物理性能的影響；泡沫混凝土能與可回收廢料相結合并得到應用，如廢海貝[10]、堿活化礦渣[11]等，這可以降低一些廢料對環境的污染。

現階段，一些工程需要考慮泡沫混凝土的動態性能。泡沫混凝土良好的吸能特性，使其能成為隧道的隔震材料[12]；飛機的攔截系統中也采用泡沫混凝土[13]，因其吸能作用，能降低飛機降落時對起落架的傷害，以及飛機能夠在降落時有效減速，不超出安全距離。因而考慮泡沫混凝土的動態性能是有必要的。在動態力學的探究中，黃海健等[14]采用φ50 mm的分離式霍普金森壓桿(split Hokinson pressure bar, SHPB)裝置對泡沫混凝土與普通混凝土進行沖擊壓縮試驗，試驗發現，普通混凝土的應變率效應要優于泡沫混凝土，同時通過分析泡沫混凝土的動態力學性能，改進朱-王-唐本構方程。Feng等[15]利用SHPB裝置對300 kg/m3、450 kg/m3、700 kg/m3三種密度下的泡沫混凝土進行沖擊壓縮試驗，試驗發現，高密度的泡沫混凝土的應變率效應顯著于低密度的泡沫混凝土，且隨著密度的增加，泡沫混凝土的動態峰值應力也隨之增加。Guo等[16]把泡沫混凝土作為緩沖層放置鋼筋混凝土之上，對四種厚度(0 mm、200 mm、400 mm、600 mm)下的緩沖層進行落錘試驗，試驗發現，泡沫混凝土作為緩沖層，明顯降低了落錘的沖擊作用，且緩沖層厚度為400 mm時，緩沖效果好而且經濟，比無緩沖層下的沖擊力下降了96%。

我國冬季氣溫偏低，特別是青藏高原地區與西北地區，最低氣溫可達-30 ℃以下。泡沫混凝土的隔熱性能好，這使得其作為保溫墻得以應用。Ekrami等[17]利用Ansys Fluent模擬了泡沫混凝土墻在嚴寒地區的儲熱性能，丁曉燕等[18]利用泡沫混凝土設計了280 mm厚、適用于東北寒區的自保溫砌塊。可見，泡沫混凝土逐漸被應用于高寒地區。此外，崔玉理等[19]還通過改變水溫以及環境溫度養護泡沫混凝土，發現,可以根據泡沫混凝土的初凝時間選擇適宜的養護溫度，水溫會影響泡沫混凝土的抗壓強度與導熱系數，且在35～40 ℃時泡沫混凝土性能最好。

然而以上對泡沫混凝土的研究僅考慮動態性能或低溫下性能中的一點，將二者結合在一起考慮的研究較少。因而本文擬通過采用φ100 mm的SHPB裝置在五種應變率下對低溫(0 ℃及0 ℃以下的溫度環境)下的泡沫混凝土試塊進行沖擊壓縮試驗。在溫度效應和應變率效應中，找出在低溫下抗動載設計中泡沫混凝土的優先考慮因素。

1 實 驗

1.1 混凝土制備

泡沫混凝土的配合比如表1所示。

表1 泡沫混凝土配合比Table 1 Mix proportion of foamed concrete

對于泡沫混凝土這種多孔型材料，為了保證其應力均勻性，試件的長徑比為0.5～0.6，本文取0.5。采用取芯機、切割機與打磨機對泡沫混凝土進行處理，得到φ100 mm×50 mm圓柱體試件，如圖1所示。

圖1 圓柱體泡沫混凝土試件Fig.1 Cylinder foamed concrete specimens

1.2 試驗裝置及試驗方法

動態力學試驗采用南陽師范學院的φ100 mm的SHPB裝置完成，如圖2所示。其中：子彈、入射桿與透射桿的直徑均為100 mm，長度分別為0.8 m、4.5 m和2.5 m。本文采用的泡沫混凝土內部孔隙孔徑較大，試件直徑過小會導致試驗數據離散性變大以及應力不均勻[20]，因此采用大直徑φ100 mm壓桿。由于泡沫混凝土的波阻抗低，為了采集到透射桿的透射波，透射桿采用半導體應變片，且所有壓桿均采用鋁桿[21]，鋁桿密度為2.85×103kg/m3，彈性模量為69.35 GPa，通過計算得其波速為4 933 m/s。

圖2 SHPB試驗裝置Fig.2 SHPB test device

根據文獻[22]，本文采用二波法處理數據：

(1)

入射波、反射波與透射波所攜帶的能量由式(2)計算可得：

(2)

泡沫混凝土吸收能用式(3)表示：

WA=Wi-Wr-Wt

(3)

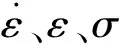
1.3 試驗方案

本文擬采用5種不同的子彈速度與5種不同的溫度對泡沫混凝土試件進行沖擊壓縮試驗，即在每種溫度下，分別采用5種子彈速度對泡沫混凝土進行沖擊試驗。子彈速度分別為3.5 m/s、4.5 m/s、5.5 m/s、6.5 m/s、7.5 m/s，溫度分別為常溫(10 ℃)、0 ℃、-10 ℃、-20 ℃、-30 ℃。入射波會出現明顯振蕩效應，需要對其整形，因而采用多孔型薄紙板作為整形器。

2 結果與討論

2.1 應力平衡

圖3 泡沫混凝土應力平衡檢驗Fig.3 Stress balance test of foamed concrete

為了保證數據的可靠性，需檢驗泡沫混凝土是否達到應力平衡。圖3給出了泡沫混凝土的入射應力、反射應力、透射應力和入射+反射應力。圖中透射應力與入射+反射應力幾乎重合在一起，說明泡沫混凝土在受沖擊作用時達到了應力平衡狀態。

2.2 應力應變曲線分析

通過二波法公式即可計算得到泡沫混凝土的動態應力應變數據，如圖4所示。試驗中有電噪聲[23]的干擾，且透射桿采用半導體應變片采集電信號，噪聲被放大，因而應力應變曲線有波動。

由圖4(a)可知，當應變率維持在100 s-1時，泡沫混凝土在不同溫度下的應力應變曲線表現出匯聚現象，匯聚趨向于溫度高(常溫)的應力應變曲線,其他4種應變率下的應力應變曲線也表現出匯聚現象。而不同應變率下的應力應變曲線有所不同，如圖4(b)所示。

圖4 泡沫混凝土的應力應變曲線Fig.4 Stress-strain curves of foamed concrete

以62.59 s-1為分界，當應變率小于62.59 s-1時，泡沫混凝土的動態應力應變曲線主要分為3個階段：

(1)線彈性階段，即0A段，加載初期，應力隨應變大致呈線性增長；

(2)屈服階段，即AB段，泡沫混凝土依靠其孔壁骨架繼續承受沖擊荷載,形成應力平臺，此時孔壁已開始發生破壞；

(3)破壞階段，即BC段，泡沫混凝土完全破壞，應力隨應變的增長而降低。

當應變率大于62.59 s-1時，泡沫混凝土的應力應變曲線主要分為5個階段，如圖4(b)所示：

(1)線彈性階段，即0A′段，此時，泡沫混凝土依靠彈性變形承擔沖擊荷載;

(2)屈服階段，即A′B′段，應力集中于泡沫混凝土內部的孔壁上，應力與應變呈現非線性關系;

(3)局部失穩，即B′C′段，當應力達到峰值后，泡沫混凝土的微裂紋擴展，應力突然下降至平臺段;

(4)應力平臺，即C′D′段，泡沫混凝土具有許多孔隙，在受到沖擊作用后，內部孔結構破壞后所產生的泡沫混凝土顆粒填充未損壞的孔結構，這能消除局部失穩并產生壓縮變形;

(5)破壞階段，即D′E′段，泡沫混凝土完全破壞，應力隨著應變的增長而降低。

應變率大小影響應力應變曲線特征的主要原因是：在較低應變率下，泡沫混凝土的破壞形式主要以均勻壓實破壞為主；隨著應變率的增加，泡沫混凝土的破壞形式由均勻壓實破壞轉向逐層塌落破壞。

2.3 應變率效應對泡沫混凝土動態性能的影響

圖5給出了不同溫度下泡沫混凝土的峰值應力與應變率之間的關系。從圖中可以看出，泡沫混凝土在虛線左側表現出明顯的應變率效應，即峰值應力隨應變率的增大而增大。超過虛線后，應變率效應則表現得不顯著。這與黃寶峰等[24]的輕質高強混凝土沖擊試驗相似，當子彈處于高速度狀態時，混凝土的應變率效應不顯著。從應變率效應顯著階段的起點到終點，泡沫混凝土在常溫、0 ℃、-10 ℃、-20 ℃、-30 ℃的動態抗壓強度分別提高了34%、15%、25%、35%、33%。

從圖5中還可以看出，隨著溫度的降低，泡沫混凝土應變率效應顯著區域與不顯著區域的分界點所對應的應變率逐漸變大，即分界點所對應的應變率從109.82 s-1增長到123.75 s-1。這說明隨著溫度的降低，泡沫混凝土的應變率效應逐漸變好。其主要原因是泡沫混凝土孔隙內含有孔溶液，當泡沫混凝土處于低溫狀態時，孔溶液形成冰，而冰在60～1 400 s-1具有較為明顯的應變率效應[25]，當溫度降低時，冰與泡沫混凝土共同承受荷載，因而泡沫混凝土的應變率效應隨著溫度的降低而提高。

圖6表示不同應變率下泡沫混凝土的吸收能與應變率之間的關系。可以看出：吸收能一開始表現出顯著的應變率效應，即吸收能隨著應變率的增加而增加；但當吸收能達到“閾值”時，便不再隨應變率增加而增加。其主要原因是隨著應變率的增加，入射能也隨之增加，根據能量守恒，泡沫混凝土需吸收能量平衡入射能，但泡沫混凝土吸收能量的能力有限，所以當入射能超過能量“邊界”且繼續增加時，吸收能便不再變化。同峰值應力的應變率效應，虛線左側為吸收能的應變率效應顯著階段，右側為應變率效應不明顯階段。此外，階段分界點的應變率隨著溫度降低也在增大，說明吸收能的應變率效應隨著溫度的降低而提高。在常溫、0～-30 ℃ 5個溫度狀態下，泡沫混凝土從應變率顯著階段的起點到終點，其吸收能分別提高了64%、123%、137%、170%、133%。

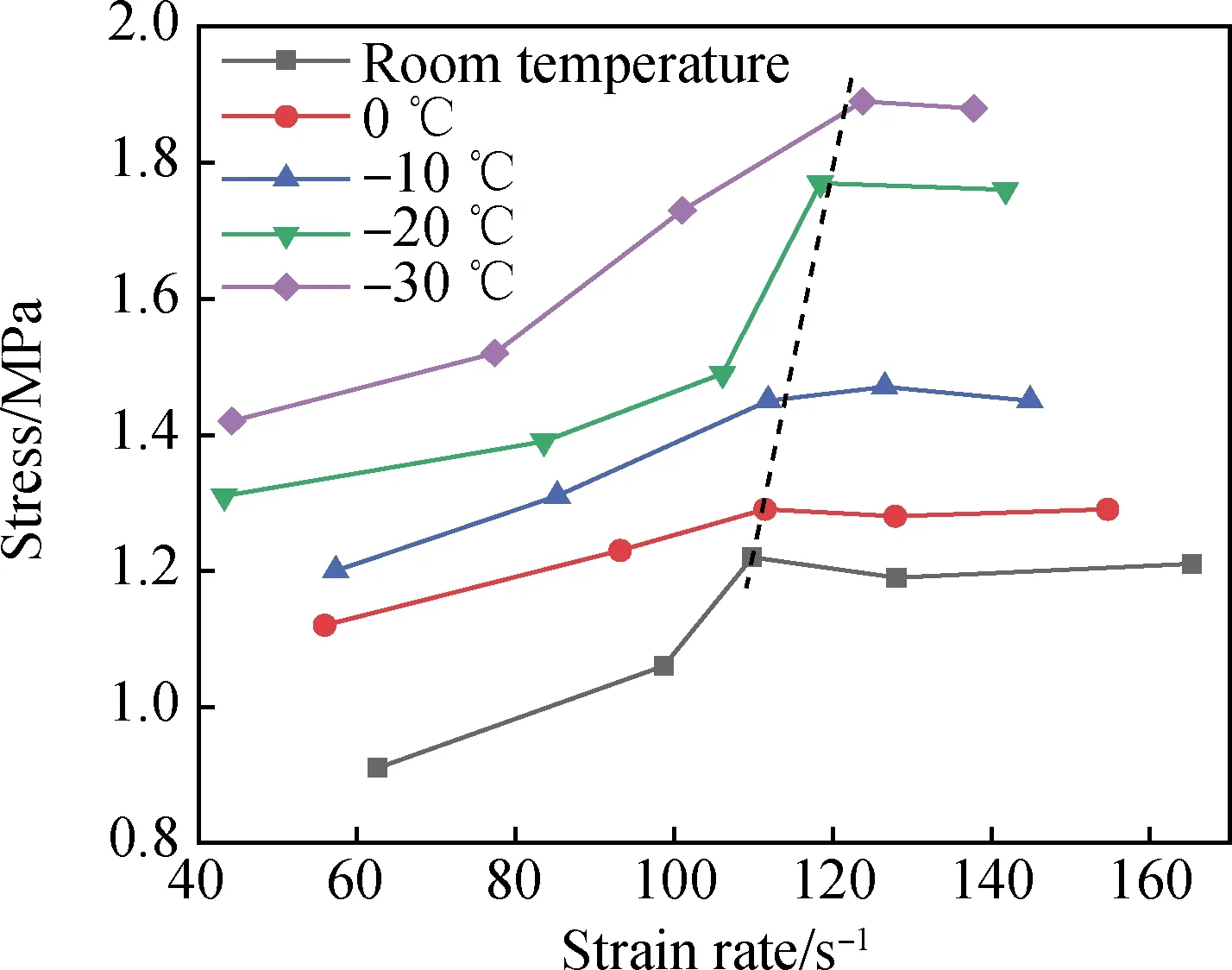
圖5 峰值應力與應變率之間的關系Fig.5 Relationship between peak stress and strain rate

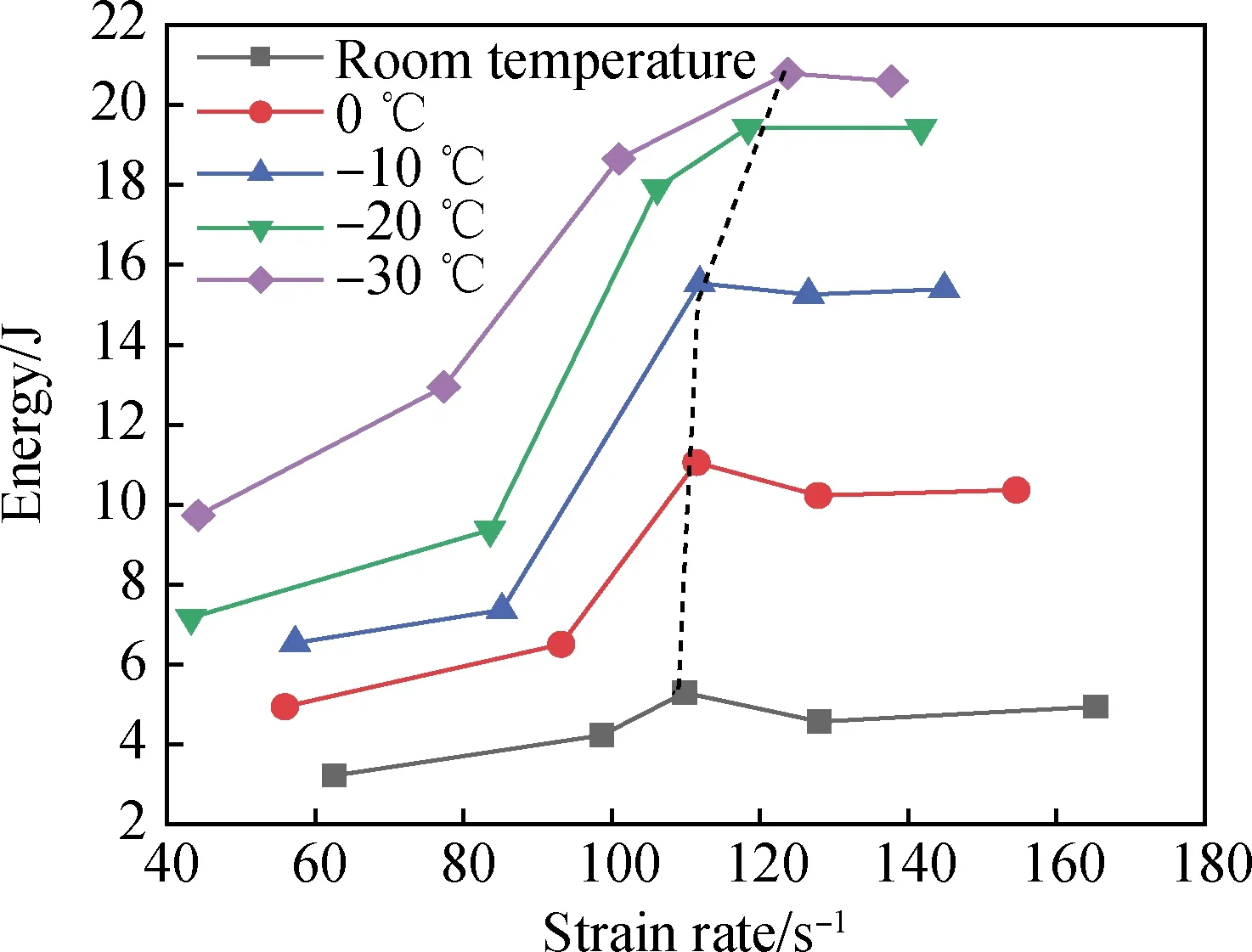
圖6 吸收能與應變率之間的關系Fig.6 Relationship between absorption energy and strain rate

2.4 溫度效應對泡沫混凝土動態性能的影響

圖7給出了不同溫度下泡沫混凝土的動態峰值應力。由圖可知，泡沫混凝土的峰值應力隨著溫度的降低而提高。從常溫下降到-30 ℃，5種子彈速度下的峰值應力分別提高了56%、44%、42%、59%、56%。其主要原因：(1)在低溫處理泡沫混凝土時，周圍空氣中的水分遇冷形成冰層并與泡沫混凝土緊密貼合，對其起到了加固的作用，因而其峰值應力得以提高；(2)泡沫混凝土為多孔隙材料，孔隙含有孔溶液，遇冷形成冰，同時孔隙內也有水汽遇冷形成冰層與孔壁緊密貼合，使得孔隙不易發生破壞；(3)泡沫混凝土為親水材料，隨著溫度降低，泡沫混凝土與冰的黏接強度也隨之提高，而在同一條件下，冰與泡沫混凝土的結合強度要大于冰的強度；(4)泡沫混凝土內含有β-H2O(易蒸發水)，隨著溫度的降低，β-H2O的含量減少，而β-H2O的消失能提高低溫下泡沫混凝土的強度。此外，由于溫度的降低，冰的動態抗壓強度也隨之增強[26]。正是由于冰的這一特性，泡沫混凝土的動態抗壓強度隨溫度的降低而提高。

為了進一步探究溫度與泡沫混凝土動態峰值應力的關系，對圖7中的數據點進行線性擬合。各個子彈速度下的擬合曲線的R2分別為0.971、0.979、0.944、0.967、0.956，這說明泡沫混凝土的動態峰值應力與溫度呈線性關系。

不同應變率下泡沫混凝土的峰值應變與溫度之間的關系如圖8所示。從圖中可以看出，泡沫混凝土的峰值應變隨著溫度的降低而降低，說明其延性隨著溫度的降低逐漸變差。隨著溫度的降低，冰的動態峰值應變也降低，而泡沫混凝土內部在低溫狀態下會形成冰，所以其峰值應變也隨溫度的降低而降低。對圖中數據進行線性擬合，發現峰值應變與溫度也呈線性關系。但擬合直線的斜率“k”都很小，說明泡沫混凝土的峰值應變隨溫度降低的降低幅度都很小。

圖7 動態峰值應力與溫度之間的關系Fig.7 Relationship between dynamic peak stress and temperature

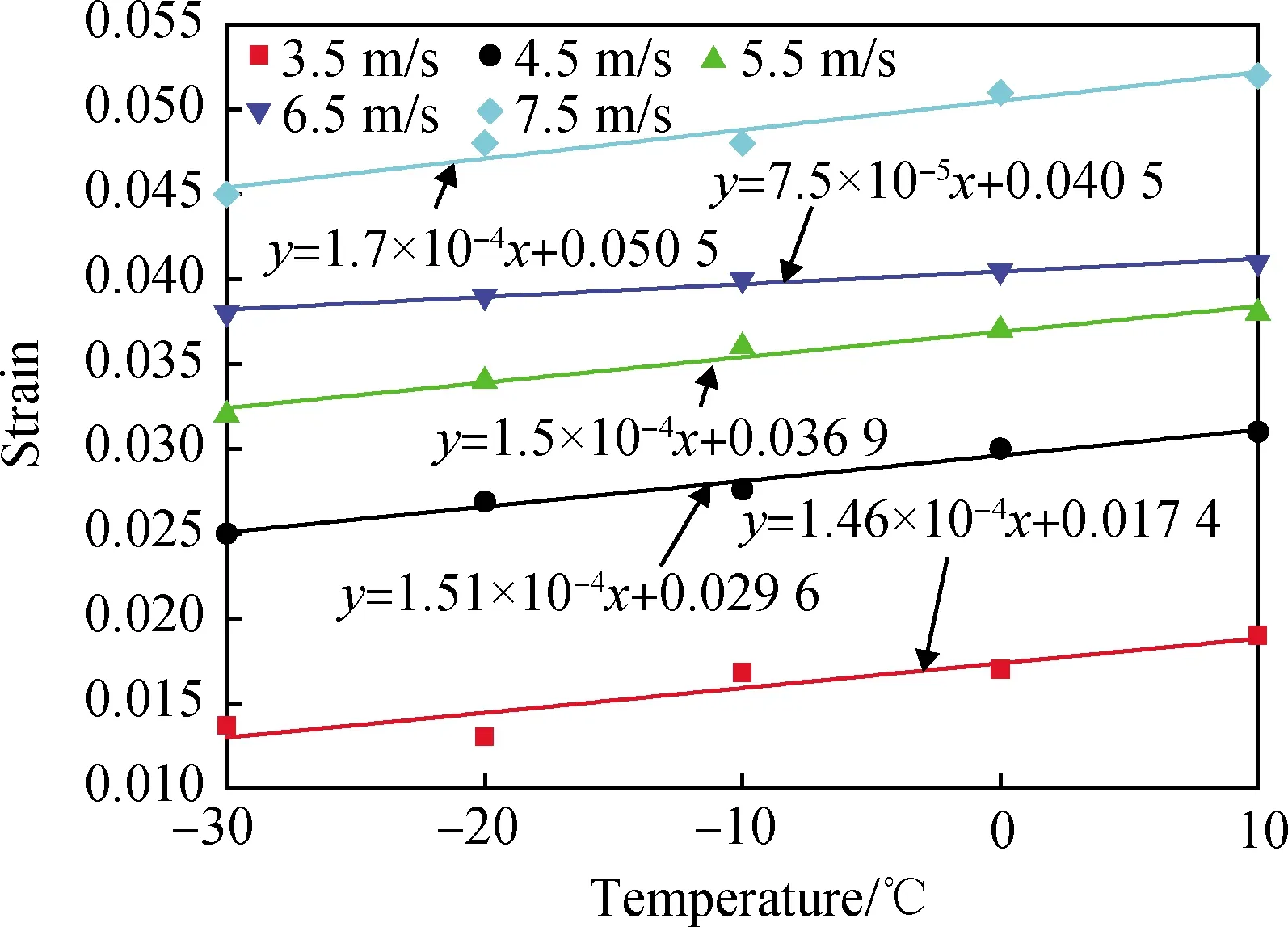
圖8 動態峰值應變與溫度之間的關系Fig.8 Relationship between dynamic peak strain and temperature

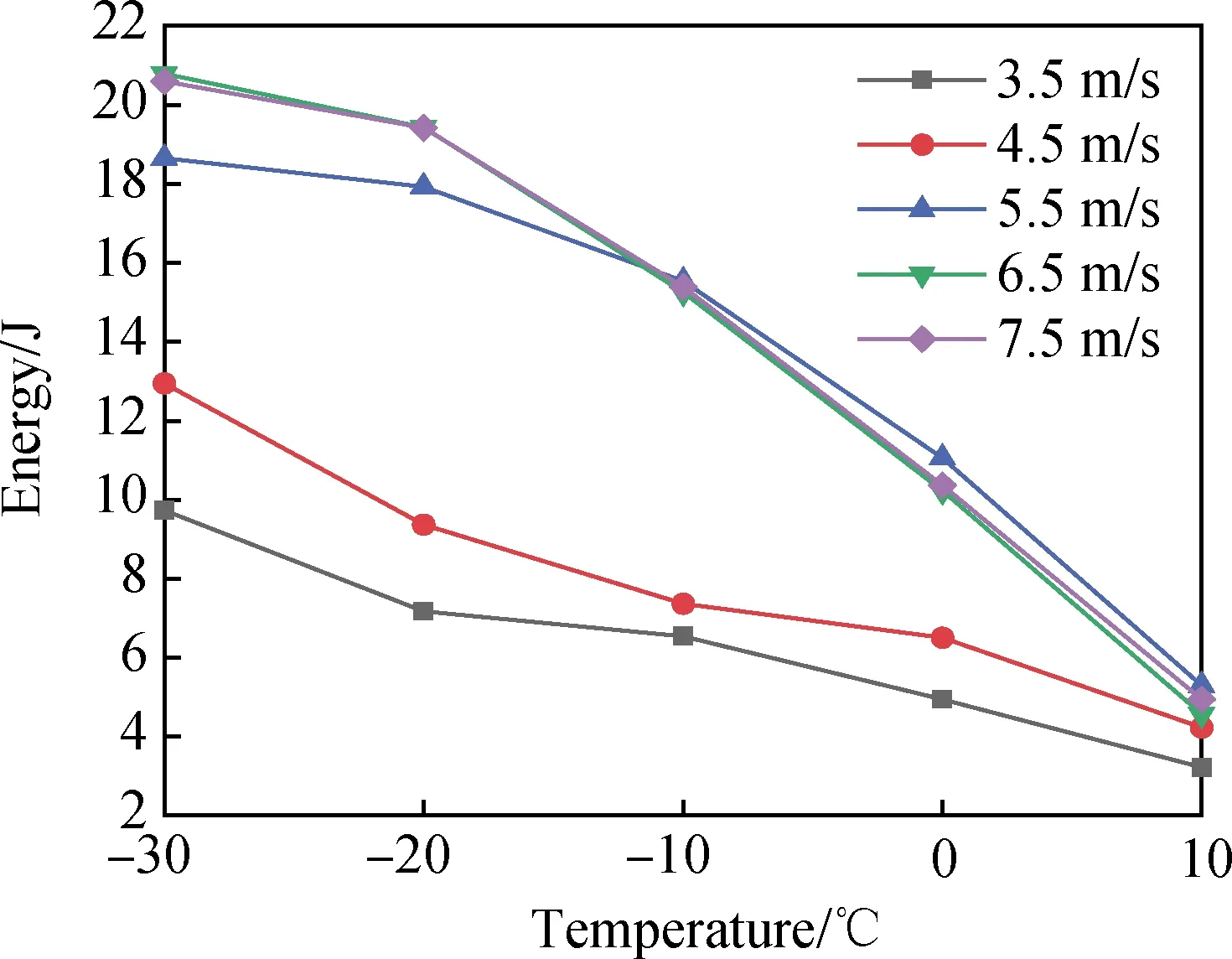
圖9 吸收能與溫度之間關系Fig.9 Relationship between absorption energy and temperature

在不同應變率下泡沫混凝土的吸收能與溫度之間的關系如圖9所示。從圖中可以看出，泡沫混凝土吸收能的溫度效應都很明顯，且其吸收能隨溫度的降低而提高。這與Qiao等[27]所得的結果一致，說明低溫使泡沫混凝土吸收更多的能量。其原因是，當溫度降低時，泡沫混凝土內部與外部都會形成冰，與泡沫混凝土共同承受沖擊壓力。而冰的破壞需要吸收比原來更多的能量，隨著溫度的降低，冰的強度也隨之提升，使其發生破壞需要吸收更多的能量，所以泡沫混凝土的吸收能不斷提高。還可以看出：當子彈速度在3.5 m/s、4.5 m/s時，溫度與吸收能大致呈線性關系；而當子彈速度增大到5.5 m/s以后，吸收能隨溫度的降低先大幅度增長，到-20 ℃后，吸收能增長幅度開始變小。

2.5 應變率效應與溫度效應對比

為了更好地對比應變率效應與溫度效應，截取泡沫混凝土應變率效應顯著階段與溫度效應進行對比。由圖5可知，在常溫、0 ℃、-10 ℃、-20 ℃和-30 ℃下，泡沫混凝土應變率效應顯著的區間分別為62.59～109.82 s-1、52.88～111.42 s-1、57.30～111.87 s-1、43.27～118.41 s-1和44.20～123.75 s-1。

本文引入η1、φ1、ψ1分別表示峰值抗壓強度、峰值應變、吸收能的溫度增長因子，η2、φ2、ψ2分別表示峰值抗壓強度、峰值應變、吸收能的應變率增長因子[27]。如式(4)表示：

(4)

式中：ηi,1、φi,1、ψi,1分別代表子彈速度i下泡沫混凝土的峰值應力、峰值應變、吸收能的溫度增長因子；σi,-30、εi,-30、Wi，-30分別代表子彈速度i、-30 ℃時泡沫混凝土的峰值應力、峰值應變、吸收能；σi，10、εi，10、Wi,10分別代表子彈速度i、10 ℃時泡沫混凝土的峰值應力、峰值應變、吸收能；i分別為3.5 m/s、4.5 m/s、5.5 m/s、6.5 m/s、7.5 m/s；ηj,2、φj,2、ψj,2分別代表溫度j下，泡沫混凝土峰值應力、峰值應變、吸收能的應變率增長因子；σj,T、εj,T、Wj,T分別代表溫度j下應變率效應作用階段泡沫混凝土的最大應變率對應的峰值應力、峰值應變、吸收能；σj,L、εj,L、Wj,L分別代表溫度j下應變率效應作用階段泡沫混凝土的最小應變率對應的峰值應力、峰值應變、吸收能；j分別為-30 ℃、-20 ℃、-10 ℃、0 ℃、10 ℃。

圖10為峰值抗壓強度、峰值應變、吸收能的溫度和應變率增長因子與應變率、溫度的關系。從圖10(a)中可以看出，η1、η2都大于1，說明溫度的降低與應變率的提高都是使泡沫混凝土的動態抗壓強度呈正增長的。η1隨應變率的增加變化不明顯，且η2隨溫度的增加變化也不顯著。從圖中還可看出η1>η2，說明溫度效應對泡沫混凝土的影響要強于應變率效應。另外，當達到一定應變率時，泡沫混凝土的應變率效應會變得不顯著，而不論何種溫度下溫度效應都很明顯，這也說明溫度效應對峰值抗壓強度影響強于應變率效應。

從圖10(b)可看出，φ1<1、φ2>1，說明溫度效應和應變率效應對應變的影響相反，即溫度的降低使應變負增長，應變率效應使應變正增長。隨著溫度的降低，φ2大致呈增加的趨勢，說明隨著溫度的降低，溫度使應變的應變率效應越來越顯著，而隨著應變率的增加，φ1越來越趨向于1，說明應變的溫度效應在逐漸減弱。φ2與1的距離大于φ1與1的距離，說明應變率效應對泡沫混凝土應變的影響更大。

圖10(c)中的ψ1、ψ2均大于1，說明溫度效應與應變率效應都使吸收能增加。在3.5～6.5 m/s之間，隨著應變率的增加，ψ1也在增加，說明在此區間內吸收能的溫度效應隨著應變率的提高而提高；在10～-20 ℃之間，ψ2隨著溫度的降低在提高，即在此區間內溫度越低，應變率效應越好。此外，還可觀察出ψ1>ψ2，得出兩種效應之中，溫度效應對吸收能的影響最大。

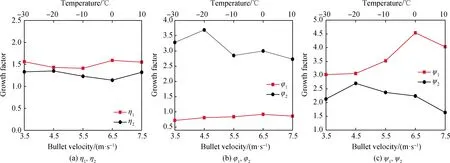
圖10 峰值抗壓強度、峰值應變、吸收能的溫度和應變率增長因子與應變率、溫度的關系Fig.10 Relationship between temperature and strain rate growth factors of peak compressive strength, peak strain, absorption energy, and strain rate and temperature

綜上所述，低溫狀態下研究泡沫混凝土時，溫度效應對其動態抗壓強度與吸收能影響更明顯，而應變率效應對其峰值應變影響更顯著。

2.6 破碎形態

圖11～圖15給出了常溫與低溫狀態下泡沫混凝土的最終破壞形態。從圖中可以看到，泡沫混凝土的部分孔隙被其孔壁破碎后形成的粉狀泡沫混凝土填充，說明其在受到壓桿撞擊時被壓實，形成了圖4(a)中應力應變曲線中的應力平臺。隨著子彈速度的增大，泡沫混凝土更傾向于逐層破壞，因而在應力應變曲線中的應力平臺會更長。泡沫混凝土的破碎塊度隨著子彈速度的增大而變小，且粉狀的泡沫混凝土也在逐漸增多，但超過一定閾值后，破壞形態差異并不大。其主要原因是泡沫混凝土完成破壞過程需要吸收能量，吸收能達到相應應變率后便不再增加，因而超過一定應變率后，破壞形態便沒發生太大變化，如圖6所示。

為探究破碎形態與溫度之間的關系，比較了低應變率下的破碎形態。隨著溫度的降低，泡沫混凝土的破壞塊度逐漸變大。選取常溫狀態與-30 ℃下的破碎樣本，發現常溫狀態下受沖擊后粉末狀泡沫混凝土明顯多于后者，這說明低溫下泡沫混凝土的整體性優于常溫狀態下，且隨著溫度的降低，泡沫混凝土的抗沖擊性能逐漸變強。盡管泡沫混凝土的吸收能隨溫度的降低而增大(見圖9)，但泡沫混凝土的整體性卻越好。這是因為泡沫混凝土在低溫狀態內部所形成的冰使水泥顆粒能更好地連接在一起，且受沖擊時，其內部的冰能替泡沫混凝土抵消部分沖擊能。

圖11 常溫狀態下泡沫混凝土的最終破碎形態Fig.11 Final crushing form of foamed concrete at normal temperature

圖12 0 ℃狀態下泡沫混凝土的最終破碎形態Fig.12 Final crushing form of foamed concrete at 0 ℃

圖13 -10 ℃狀態下泡沫混凝土的最終破碎形態Fig.13 Final crushing form of foamed concrete at -10 ℃

圖14 -20 ℃狀態下泡沫混凝土的最終破壞形態Fig.14 Final failure form of foamed concrete at -20 ℃

圖15 -30 ℃狀態下泡沫混凝土的最終破壞形態Fig.15 Final failure form of foamed concrete at -30 ℃

3 結 論

(1)當應變率小于62.59 s-1時，泡沫混凝土的應力應變曲線分為3個階段：線彈性階段、屈服階段、破壞階段；而應變率大于62.59 s-1時，應力應變曲線分為線彈性階段、屈服階段、局部失穩、應力平臺、破壞階段5個階段。在同一應變率作用下，不同溫度下的應力應變曲線具有匯聚現象，匯聚趨向于溫度高(常溫)的曲線。

(2)泡沫混凝土的動態抗壓強度，吸收能在常溫、0 ℃、-10 ℃、-20 ℃及-30 ℃的應變率效應顯著階段分別在62.5～109.82 s-1、52.88～111.42 s-1、57.30～111.87 s-1、43.27～118.41 s-1及44.20～123.75 s-1。當應變率超過分界點，應變率效應便不再顯著。應變率效應分界點的應變率數值隨著溫度的降低而增加，說明溫度的降低提高了泡沫混凝土的應變率效應。

(3)泡沫混凝土的峰值抗壓強度、吸收能、峰值應變具有溫度效應，峰值抗壓強度與吸收能隨著溫度的降低而提高，且峰值抗壓強度與溫度呈線性關系，但是峰值應變隨溫度的降低而變小。破碎塊度隨溫度的降低而變大。

(4)在低溫環境下，影響泡沫混凝土動態抗壓強度和吸收能的首要因素是溫度效應，影響泡沫混凝土動態峰值應變的首要因素是應變率效應。