直線法修形擺線針輪副的回程誤差

李玉龍，李天興，李晉凡，張瑞瑤，周靜遠

(河南科技大學 機電工程學院，河南 洛陽 471003)

0 引言

在機器人精密減速器中，擺線輪修形的目的在于保證非工作區域合理的間隙，便于安裝和潤滑，保證工作區域齒廓與擺線輪理論齒廓盡可能地接近，保證良好的輪齒嚙合特性[1-4]。隨著擺線輪成形磨削技術的不斷發展，擺線輪的修形方法也不再局限于傳統的移距、等距等修形方式，修形齒廓形狀也呈現多樣化[5-8]。然而，多樣化齒廓形狀的傳動精度的求解并沒有形成統一的求解模型，對準確評價擺線輪修形齒廓的嚙合性能產生了一定的影響。機器人精密減速器經常需要做往復運動，修形后的擺線輪由于嚙合間隙以及回程誤差的存在[9-12]，使整個系統的重復定位精度受到嚴重影響。因此，不同修形齒廓的擺線輪回程誤差的獲取和分析已成為該領域研究的重要內容。

目前，學者對機器人精密減速器擺線輪齒廓的修形、擺線針輪嚙合特性和傳動精度等方面已經進行了深入的研究。文獻[13]綜合考慮制造誤差對擺線針輪嚙合傳動的不良影響，提出了一種新型的正等距與負移距組合的修形方式，增加了共同嚙合齒數，提高了承載能力，縮小了回程誤差。文獻[14]對擺線輪傳統修形方法所產生的回程誤差做了詳細研究，計算出回轉角的變化范圍。文獻[15]研究了擺線輪單齒無側隙失配修形，并推導出擺線輪修形后的齒廓方程。文獻[16]通過建立擺線針輪齒廓修形的回程誤差精度分析模型，可求解常見修形方法引起的幾何回差誤差，并推導出擺線輪齒廓修形回差誤差的影響公式。文獻[17]基于傳統修形模式，通過建立齒面接觸分析(tooth contact analysis,TCA)方程，提出一種適用于各種修形模式的嚙合間隙計算方法。文獻[18]在拋物線修形方法的基礎上，綜合考慮齒廓誤差和傳動誤差影響，獲得更加符合工程實際的擺線輪齒廓。

盡管國內外學者已經在擺線輪齒廓修形和回程誤差分析方面取得了較大成果，但是傳統的回程誤差的獲取相對復雜。隨著擺線輪修形齒廓形狀的多樣化，需要建立一種通用的修形齒廓回程誤差的求解模型，有助于形成統一的回程誤差評價體系。因此，本文基于直線法修形齒廓，通過建立擺線針輪接觸模型，求解回程誤差，獲取理論修形齒廓回程誤差曲線，研究機器人精密減速器的回程誤差性能，可為改善系統的重復定位精度提供新思路。

1 直線法修形齒廓及其方程

直線法修形是一種簡單有效的齒廓設計方法，它綜合考慮了壓力角與修形量的影響關系，能夠獲得具有良好傳力性能的齒廓形狀。

1.1 直線法修形

直線法修形是使修形量ΔL與壓力角α滿足線性關系，建立修形量與壓力角的函數關系[19]：

ΔL=kα+b1。

(1)

將已知參考點坐標(α0,ΔL0)、齒頂坐標(αtip,ΔLtip)代入式(1)，可求解出未知參數k、b1，即可得到從參考點到齒頂的修形量表達式，同理，將參考點和齒根坐標代入方程(1)，整理得出參考點到齒根的修形量表達式。

直線法修形量的分段函數表達式[19]：

(2)

其中：αroot為齒根處壓力角；ΔLroot為齒根處修形量。

1.2 修形齒廓方程

將式(2)求得的修形量沿理論齒廓各個點的法線方向依次進行疊加，直線法修形原理如圖1所示。

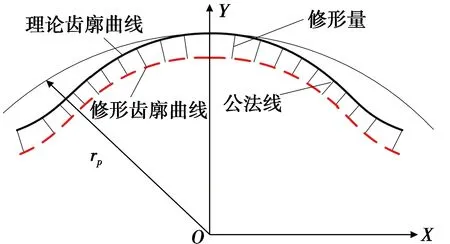
圖1 直線法修形原理圖

圖1中，實線為擺線輪理論齒廓曲線，虛線為修形齒廓曲線，虛線與實線之間是法線。

修形后擺線輪齒廓方程為：

(3)

2 擺線針輪的嚙合接觸分析模型

根據擺線針輪副嚙合傳動關系建立坐標系，擺線輪嚙合關系如圖2所示。圖2中，坐標系Sp(XpOpYp)與Sc(XcOcYc)固接到相對于固定坐標系Sf(XfOfYf)進行轉動的針輪和擺線輪上，Op為針輪自轉坐標系中心，Oc為擺線輪自轉坐標系中心，K為嚙合點，M為針齒圓心，P為節點，PM為公法線。針齒的齒廓方程為：

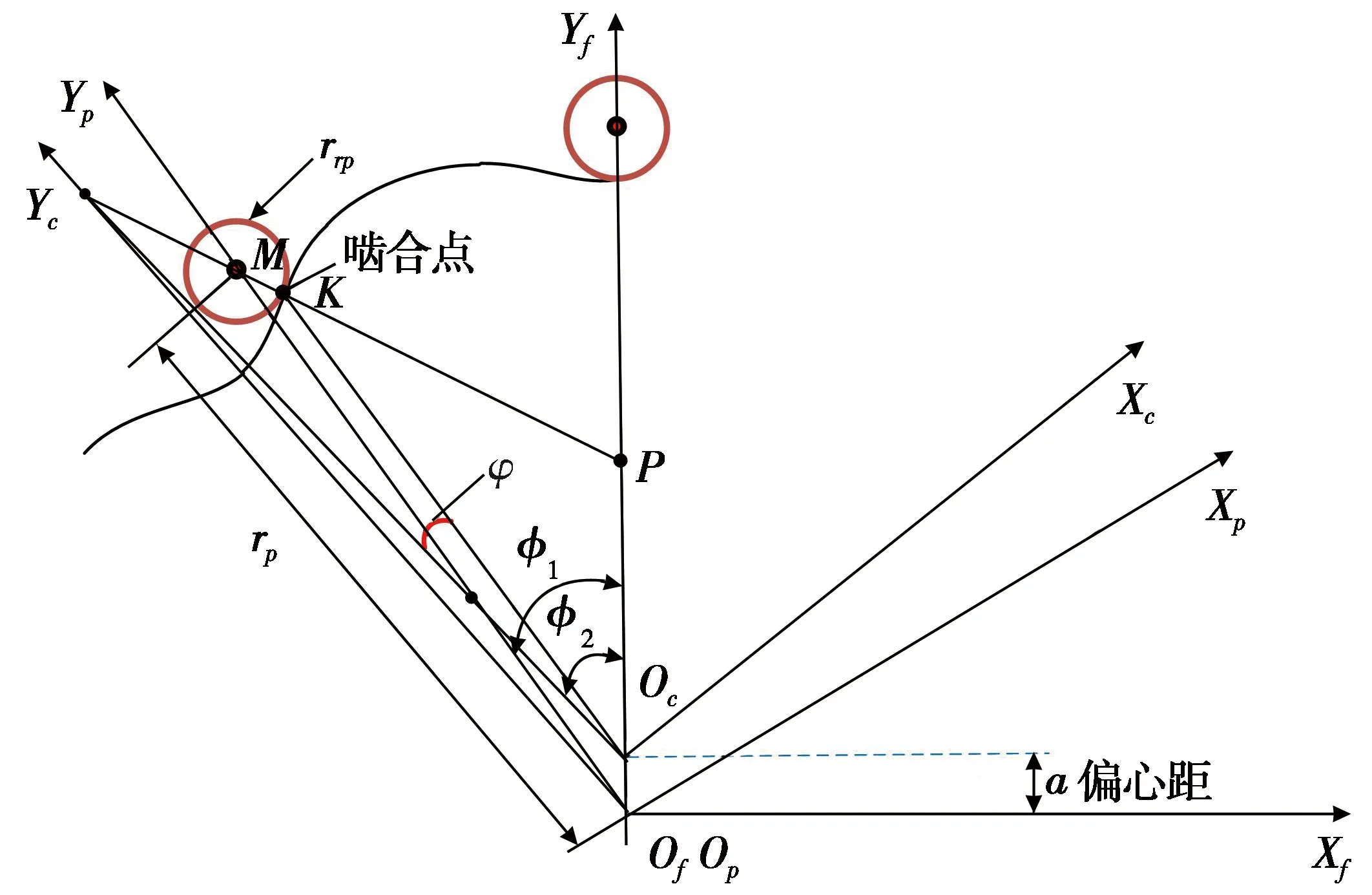
圖2 擺線輪嚙合關系

(4)

其中：p為針齒參量角。

在擺線針輪嚙合傳動過程中，在嚙合接觸位置，擺線輪與針齒的位置矢量和法線矢量應相等[20]，通過空間坐標轉換，將擺線輪和針輪的位置矢量和法線矢量轉化到固定坐標系Sf中，由此建立擺線針輪副的嚙合接觸分析數學模型：

(5)

其中：φ1為針輪轉角；φ2為擺線輪轉角；β為針齒參量角；Mfp和Mfc均為變換矩陣。

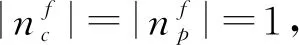
(6)

方程組(6)是非線性的，有3個方程和4個未知數[22]，給定φ，即可求解出對應的φ1、φ2和β值。

3 回程誤差的獲取

修形后的擺線輪與針輪之間會產生一定的間隙，當擺線輪往復運動時，需要克服齒側間隙才能進入反向嚙合傳動。以11齒擺線輪為例，擺線針輪嚙合的瞬時狀態如圖3所示。

由式(6)可以得到擺線輪嚙合范圍，以及擺線針輪嚙合傳動時擺線輪和針輪的轉角。如圖3所示，當前0號齒處于嚙合狀態，針輪反向轉動，齒側間隙最小的齒對會最先進入嚙合，針輪的最小回轉角即回程誤差[21]。在獲得擺線針輪接觸分析結果的基礎上，根據求解過程，可以得到回程誤差。回程誤差具體求解過程如圖4所示。

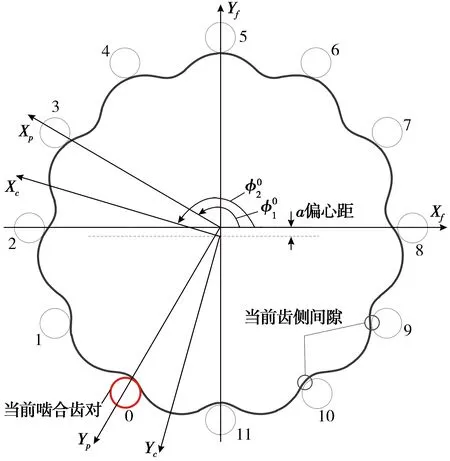
圖3 擺線針輪嚙合的瞬時狀態

圖4 回程誤差具體求解過程

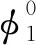
(Ⅴ)繪制回程誤差曲線。以針輪轉角作為橫坐標，消除回程間隙所轉過的角度為縱坐標。

4 驗證分析

擺線針輪副基本參數：擺線輪齒數ZC=39，針輪齒數ZP=40，針輪分布圓半徑rp=82 mm，針輪半徑rrp=3.5 mm，偏心距a=1.5 mm。

直線法修形參數為：ΔL0=0.005、ΔLtip=0.02，對應的壓力角大小為：α0=42°、αtip=90°。將以上數據代入式(1)，可求得k=3.125×10-4，b=-8.125×10-3，則直線法修形量方程為：

ΔL=3.125×10-4α-8.125×10-3。

(7)

通過式(7)，可求得任意壓力角處的ΔL。

根據直線法修形原理，將修形量ΔL依次沿著法線方向垂直疊加，可得到擺線輪直線法修形齒廓。將式(7)代入式(3)，可以得到理論的擺線輪直線法修形齒廓。然后將式(4)和式(3)代入輪齒接觸分析方程式(5)。

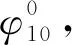
采用上述擺線針輪副基本參數，通過上述方法將得到每一嚙合齒對的回程轉角，就能夠得出直線法修形后的回程誤差曲線，如圖5所示。

圖5 回程誤差曲線

由圖5可知：直線法修形后的擺線齒廓最小回程誤差值是0.604′。為了驗證理論回程誤差計算值的準確性，加工擺線輪樣品，測量擺線輪加工后的回程誤差。

采用擺線輪成形磨齒機加工擺線輪，如圖6所示。在測量儀上完成擺線輪齒廓合理性檢測，排除其他因素的影響。

(a) 擺線輪加工

最后，將加工的擺線輪樣品在旋轉矢量(rotary vector,RV)減速器綜合性能測量儀上進行測量，獲取樣品擺線輪的回程誤差曲線，如圖7所示。

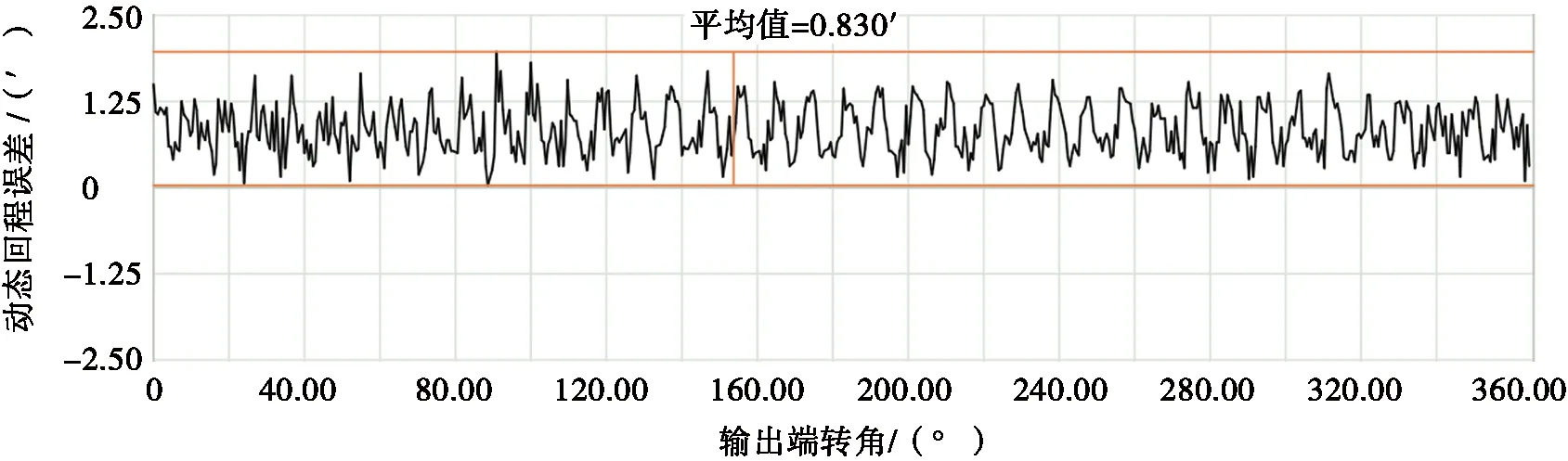
圖7 樣品擺線輪回程誤差曲線

由圖7可以看出：直線法修形后的擺線輪的實際回程誤差平均值為0.830′。因為擺線輪在實際加工的過程中，存在安裝、制造等誤差因素，因此，實際加工的擺線輪回程誤差會大于理論設計齒廓的回程誤差。通過對比圖5和圖7的數據可知：理論計算的回程誤差是實際減速器測量回程誤差的73%，在實際生產中可以用來評價回程誤差，進而評價修形質量，有一定的實際工程意義。

5 結論

本文通過結合直線法修形，以直線法修形齒廓為基礎，建立并求解輪齒接觸分析方程，獲取回程誤差曲線，驗證對比實際測量擺線輪的回程誤差曲線，理論計算的回程誤差是實際減速器測量回程誤差的73%，能夠滿足實際工程要求。因此，通過輪齒接觸分析獲取回程誤差的方法是合理、可行的，能夠高效計算出擺線針輪副的回程誤差，可作為評定齒廓修形質量的方法。