模糊變異算子的改進鴿群優化算法

夏小剛，羅建婷，王 欣

(西安科技大學 理學院，陜西 西安 710054)

0 引言

鴿群優化算法(pigeon-inspired optimization, PIO)是文獻[1]在2014年提出的一種模擬鴿子歸巢行為的新型群體智能優化算法。當前鴿群優化算法研究主要集中在優化算法改進、理論研究和工程應用3個方面。優化算法改進即通過對算法中2個相互獨立的迭代部分進行研究進而實現算法改進[2-4]； 理論研究即進一步完善算法的理論基礎[5-7]； 而工程應用即將算法應用于解決工程實際問題中[8-11]，目前主要用于解決機器人、無人機路徑規劃問題等。鴿群優化算法雖然收斂速度快，但鴿群信息之間交互不足，且易于早熟收斂、陷入局部最優[12]。為此，文獻[13]采用鞏固參數簡化傳統鴿群優化算法的結構，實現了兩個算子的平滑過渡，又將自組織映射與改進的鴿群優化算法相結合，更好地控制決策空間并找到解的當前分布。文獻[14]將延遲因子引入位置更新公式，提高了鴿群優化算法的收斂速度。文獻[15]將鴿群優化算法引入到粒子波算法中，從而提高了粒子波算法的精度和穩定性。文獻[16-17]將鴿群優化算法與其他算法相融合，相互補充和促進，形成的混合優化算法可更好地解決無人機路徑規劃問題。

雖然近年來在鴿群優化算法改進方面取得了一定的研究成果，但優化算法仍存在位置更新公式全局搜索能力弱、多樣性欠佳等不足。本文受差分進化算法(differential evolution, DE)的啟發，在地圖和指南針算子與地標算子的位置更新公式中引入模糊交叉變異算子，提出了一種改進的鴿群優化(improved pigeon-inspired optimization，IPIO)算法。借助仿真實驗和對旅行商問題(traveling salesman problem,TSP)[18-19]的測試，驗證了改進的鴿群優化算法有利于增加種群多樣性，避免算法過早陷入局部最優，能夠有效提高種群的收斂速度，增強算法的全局搜索能力。

1 改進的鴿群優化算法

1.1 鴿群優化算法的基本理論

PIO主要由兩個算子構成：地圖和指南針算子，地標算子。在地圖和指南針算子中，由式(1)和式(2)確定第i只鴿子在第t次迭代中的位置Xi和速度Vi：

Xi(t)=Xi(t-1)+Vi(t)；

(1)

Vi(t)=Vi(t-1)·e-Rt+rand·(Xg-Xi(t-1))，

(2)

其中：R為地圖和指南針因子；rand∈[0,1]；Xg為第t次迭代中的最好位置；Vi(t)為第t次鴿子的當前速度；Xi(t)為第i只鴿子在第t次迭代中的當前位置。

在地標算子中，每一代鴿子的數量都會減少1/2，用Np來記錄每一代鴿子的數量。排序接近目的地的鴿子根據式(4)計算剩余鴿子的中心位置，以此作為地標來更新自己的位置。

(3)

(4)

其中：Np(t)為第t代鴿群的數量；Xc(t)是第t代鴿子飛近目的地時作為參考方向的中心位置(期望目的地)；Fitness(Xi(t))是適應度值，對每只鴿子的適應度值[16]進行評估并排序，找到最優路徑。式(5)對鴿群位置進行越界處理，更新鴿群位置。

Xi(t)=Xi(t-1)+rand·(Xc(t)-Xi(t-1))。

(5)

1.2 模糊交叉變異的實現

針對種群中的每一個體Xi=(xi,1,xi,2,…,xi,n)，由模糊變異式(6)進行變異操作：

Wi=γ·xr1+(1-γ)·F·(xr2-xr3)，

(6)

其中：xr1為當前種群中適應度值最好的個體；xr2和xr3為群體中隨機選取的個體；F∈[0,2]為比例因子，比例因子F保證了種群的多樣性和搜索能力，大多數函數F的最優值為0.5～1.0；γ∈[0,1]為模糊參數，模糊參數γ表示變異算子的開發和貪婪程度，用于擴大局部和全局搜索能力[20]。

依據式(6)得到的變異種群Qi=(qi,1,qi,2,…,qi,n)，由式(7)進行交叉操作，得到新的種群Mi=(mr,1,mr,2,…,mr,n)。對排序接近目的地的鴿子進行越界處理，若Mi支配Xi,則用Mi代替Xi；若Xi支配Mi，則直接丟棄Mi。若互不支配，則將Mi加入Xi。交叉公式為：

(7)

其中：CR為交叉概率，取值(0,1)，即randβ∈(0,1)；β是在{1,2，…，n}中隨機選取的數。

1.3 位置更新公式的修正

模糊交叉變異算子有利于種群之間的信息交換，保證種群多樣性，擴展種群的全局搜索范圍，據此在更新公式中引入模糊交叉變異算子，并提高算法的全局開發能力和局部搜索能力。通過隨機選擇解空間中的個體來調節鴿子的位置，從而增強群體的多樣性和全局探索能力。

改進的鴿群優化算法的地圖和指南針算子的位置更新公式為：

Xi(t)=Xi(t-1)+Vi(t)+Wi，

(8)

地標算子的位置更新公式為：

Xi(t)=Xi(t-1)+rand·(Xc(t-1)-Xi(t-1))+Wi，

(9)

其中：Wi為模糊交叉變異算子。由式(8)和式(9)可以看出：與式(1)和式(5)相比，式(8)和式(9)增加了模糊交叉變異算子，從而達到對傳統鴿群優化算法位置更新公式的修正。

1.4 改進鴿群優化算法流程圖

本文提出的改進算法流程圖如圖1所示。根據式(2)和式(5)可以看出，傳統鴿群優化算法的位置更新公式只考慮了鴿子的當前位置和鴿群最優位置，由鴿群最優位置進行搜索，忽略了算法的搜索能力。受差分進化算法的啟發，在傳統鴿群優化算法中的位置更新公式中引入模糊交叉變異算子，位置更新公式的修正如式(8)和式(9)所示，引導種群變異，增加種群的多樣性，提高算法的全局搜索能力。

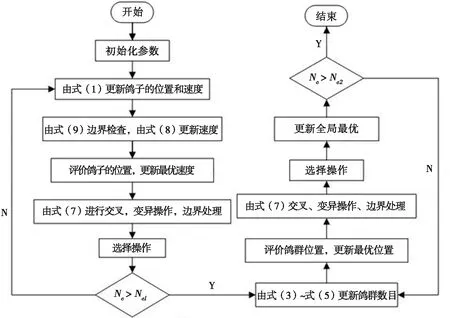
圖1 改進算法流程圖

2 實驗結果分析

2.1 測試函數及參數設置

表1給出DE、粒子群算法(particle swarm optimization，PSO)、PIO、IPIO這4種算法在19個標準測試函數中分別進行20次實驗的結果，分別記錄4種算法的最優適應度值(Optimal)、平均適應度值(Mean)和方差(Variane)。其中，最優適應度值反映解的質量；平均適應度值反映算法的收斂速度；方差反映算法的穩定性和魯棒性。將表1中最優適應度值和平均適應度值達到理論最優值的數據均標注為粗體，最優個數表示達到最優適應度值及平均最優適應度值的個數。19個標準測試函數即Schwefel’s problem 2.22(f1)、Sphere(f2)、Schwefel 2.21(f3)、Rosenbrock(f4)、Step(f5)、Quartic(f6)、Goldstein-Price(f7)、Hartmann 6-Dimensional(f8)、Shekel(f9)、Generalized Schwefel’s(f10)、Rastrigin(f11)、Ackley(f12)、Griewank(f13)、Levy(f14)、Levy n.13(f15)、De Gong Function n.5(f16)、Kowalik(f17)、Camel(f18)、Branin(f19)。其中，f1～f9是單峰函數，f10～f19是多峰函數。實驗中4種算法參數設置如下：種群規模50，最大迭代次數為1 000，比例因子設為0.5[21]，模糊參數設為0.5。實驗在MATLAB2018b軟件中進行編程運行。

2.2 實驗結果分析

從表1可以看出： IPIO在f2、f7、f8、f10、f11、f13和f19均能收斂到理論最優值。對于其他測試函數，IPIO雖然沒有收斂到理論最優值，但其獲取的適應度值與理論最優值十分接近。對于函數f7、f18和f19，4種算法都能取得相同的理論最優值。對于函數f5，傳統PIO取得了理論最優值。此外，DE有3個測試函數取得理論最優值，PSO有4個測試函數取得理論最優值。DE與PSO相比，尋優能力差不多，雖然DE和PSO求解最優適應度方面效果較差，但2個算法的穩定性較好。IPIO獲取的尋優個數為18個，尋優率達到了94.7%，相較于傳統PIO尋優個數提高了9個，尋優率提升了47.3%，取得了較好的最優適應度值、平均適應度值和方差，尋優能力均優于其他3種對比算法。

表1 4種算法在標準測試函數中適應度值比較

選出具有代表性的3個測試函數f8、f9、f10，4種算法在測試函數上的收斂曲線如圖2所示。

(a) f8的收斂曲線 (b) f9的收斂曲線 (c) f10的收斂曲線

圖2a表明：在求解函數f8時，4條曲線均為先快速下降，在50次至200次迭代后趨于穩定，PIO雖然在200次迭代后跳出局部最優，但求解精度不如其他3種對比算法。DE和PSO在前期收斂速度較快，但后期均陷入局部最優。IPIO收斂速度不僅快，而且比其他3種算法的求解精度高。圖2b表明：在求解函數f9時，其他3種函數都過早地陷入局部最優，IPIO在早期收斂速度較慢，但分別在200次和700次迭代后跳出局部最優，因此可以得出IPIO的求解精度相比其他3種算法有了顯著提高。圖2c表明：在求解函數f10時，PSO過早地陷入局部收斂，DE和PIO前期下降速度幾乎相同，PIO和IPIO都在700次迭代后跳出局部最優，但IPIO得到一個更好的適應度值。IPIO顯然比其他3種算法求解精度高，且有效地避免算法陷入早熟收斂，可得到較好的結果。

3 改進鴿群優化算法求解旅行商問題

本文算法參數仿真均以TSPLIB數據集中的dantzig42問題作為測試數據，dantzig42問題是TSPLIB數據集中的一個數據文件，城市規模為42，已知最優解為699，運行10次。IPIO與其他3種對比算法的仿真實驗結果如表2所示。

由表2可以看出：無論是平均最優值還是相對誤差，改進算法均優于其他3種對比算法。在10次仿真結果中，IPIO有3次仿真實驗達到理論最優解，平均最優值為700.3，且大多數數據都集中在最優解范圍內，相對誤差為0.19%。這表明對于dantzig42問題，IPIO的求解精度優于其他3種對比算法。除了單純的數據，可以通過路徑仿真圖來模擬4種算法在實際中的最優路徑效果。圖3給出了4種算法對dantzig42問題的路徑優化結果圖，根據路徑圖的線路復雜程度可以看出IPIO較其他3種對比算法效果更好。

表2 4種算法仿真實驗結果對比

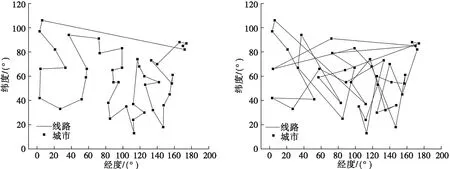
(a) DE優化結果圖 (b) PSO優化結果圖

4 結論

(1)IPIO在平均適應度值方面優于DE、PSO和PIO。IPIO在尋找最優適應度值方面優于DE、PSO和PIO。

(2)IPIO能夠跳出局部最優，避免早熟收斂，增強算法的全局搜索能力。

(3)IPIO能有效提高TSP的最優解。