Ricci 孤立子的勢函數?

李金楠， 高 翔

(中國海洋大學數學科學學院， 山東 青島 266100)

20世紀80年代，Hamilton[1]引進了Ricci孤立子的概念，Ricci孤立子是愛因斯坦度量的自然推廣且為解決三維龐加萊猜想的主要工具。同時Ricci孤立子對應于Ricci流的自相似解[2-3]且出現在Ricci流方程的奇異點經伸縮變換后的極限中[4-6]。

黎曼度量gij為愛因斯坦度量若其Ricci張量滿足：

Rij=ρgij，

式中ρ為常數。特別地，具有愛因斯坦度量的光滑流形稱為愛因斯坦流形。

光滑流形Mn上的一個完備黎曼度量gij稱為Ricci孤立子，若存在一個光滑向量場V=(Vi)使其Ricci張量滿足：

式中ρ為常數。此外，若V為一個梯度向量場，則有梯度Ricci孤立子滿足方程：

Rij+▽i▽jf=ρgij。

式中f為流形Mn上的光滑函數，稱f為Ricci孤立子的勢函數。由于常數ρ取值不同，所以可將Ricci孤立子進行分類，其中ρ=0稱為穩定Ricci孤立子，ρ>0稱為收縮Ricci孤立子，ρ<0稱為擴張Ricci孤立子。

愛因斯坦流形是梯度Ricci孤立子勢函數為常數的特例，也稱為平凡孤立子，可見勢函數對于Ricci孤立子的分類具有十分重要的作用。此外結合余面積公式與勢函數估計還可進一步給出孤立子的體積增長估計，并最終應用于研究孤立子的分類問題。因此研究Ricci孤立子的勢函數估計對孤立子的分類及其他幾何不變量的研究都具有十分重要意義。

Bakry-Emery Ricci張量定義為：

Ricf=Ric+Hessf。

Bakry-Emery[7]對該張量進行了詳細研究并拓展應用解決了許多重要的孤立子問題。特別地，當勢函數f為常數時，Bakry-Emery Ricci張量即為Ricci張量，因此很多關于Ricci張量的性質及結果可以自然地推廣到Bakry-Emery Ricci張量上。本文我們將主要證明一個關于Bakry-Emery Ricci張量的Ambrose 型結論，并得到一些Ricci孤立子勢函數上下界更精確的估計結果。

1 預備知識

首先，關于流形的緊致性，Ambrose[8]證明了如下定理。

引理1設在完備黎曼流形M上存在點p使得任意從點p出發的測地線γ(t)滿足：

則M為緊致的。

推廣到Bakry-Emery Ricci張量，張世金[9]證明了對應的Ambrose-Myers型結果。

引理2設在完備黎曼流形(M,g,f)上存在點p使得任意從p出發的測地線γ(t)滿足

且勢函數滿足

f(x)≤C(d(x,p)+1)，

式中C為常數，d(x,p)為從點p到點x的距離函數，則流形M為緊致的。

此外，張世金[9]還給出了以下結論。

引理3一個完備黎曼流形M若滿足

Ricf≥λg

及

f(x)≤C(d(x,p)+1)，

式中λ>0，C為常數，則M為緊致的。

2 主要結果

改變勢函數上界條件可將引理3進一步推廣到Bakry-Emery Ricci張量上，因此我們給出以下定理：

定理1一個完備的黎曼流形(M,g,f)若其Bakry-Emery Ricci張量滿足

Ricf≥-λg，

λ>0為常數，固定點p∈M，同時勢函數f滿足

f(x)≤-δ(d(x,p)+C)2，

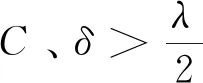
應用上述結果并結合孤立子性質[10-11]，將得到一些梯度Ricci孤立子的勢函數上下界估計結果。

定理2令(Mn,gij,f)為一個具有非負Ricci曲率的完備非緊致擴張梯度Ricci孤立子，標準化滿足

則其勢函數f滿足估計：

式中r(x)=d(x,p)為點x到固定點p∈M的距離函數；C為僅取決于維數n及單位球Bp(1)的度量gij的常數。

結合Bakry-Emery Ricci張量，張世金[9]還給出了有關收縮Ricci孤立子的經典勢函數下界估計結果[10]，利用本文結論可給出該結論的其他證明方法。

推論1令(Mn,gij,f)為一個完備非緊致的收縮梯度Ricci孤立子且

則勢函數f滿足：

式中：r(x)=d(x,p)為距離函數；C>0為僅取決于流形的維數n及單位球Bp(1)的度量gij的常數。

同理，推廣到穩定梯度Ricci孤立子，將得到以下推論。

定理3令(Mn,gij,f)為一個具有正Ricci曲率的完備非緊致穩定梯度Ricci孤立子，則其勢函數f滿足下界估計：

f(x)≥-C(r(x)+1)。

式中：r(x)=d(x,p)為距離函數；C>0為僅取決于維數n及單位球Bp(1)的度量gij的常數。

3 主要方法及證明

本節將推廣利用Wraith[12]的方法給出滿足Bakry-Emery Ricci張量下界為負常數主要定理的證明。

定理4一個完備黎曼流形(M,g,f)若滿足

Ricf≥-λg，

λ>0為常數，同時固定點p∈M，勢函數f滿足

f(x)≤-δ(d(x,p)+C)2，

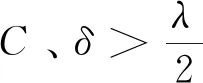
證明 (反證法)設黎曼流形M為非緊致的，固定點p∈M及單位速度射線γ(t)，γ(t)滿足初始條件γ(0)=p(即測地線γ(t)從點p出發)。任意時間t，令m(t)為以點γ(t)為中心、以t到p的距離為半徑的距離球面的平均曲率，這里以單位內法向量計算平均曲率。值得注意的是，對任意射線γ(t)，t>0時函數m(t)為光滑的，且Wraith[12]證明m(t)滿足 Riccati不等式：

代入即Bakry-Emery Ricci張量滿足：

由于

[▽f,γ′](t)-[▽f,γ′]。

由假設Ricf≥-λg，故對任意時間t>1，有

-λ(t-1)-m(1)+[▽f,γ′]。

令C1=λ-m(1)+[▽f,γ′](1)，上述不等式為

另外，由定理假設f(x)≤-δ(d(x,p)+C)2可知f(γ(t))≤-δ(t+C)2，則

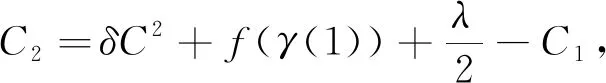
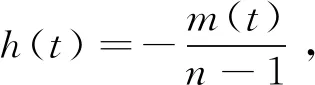
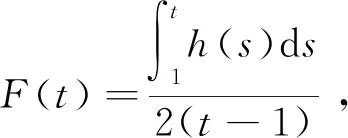
則任意t≥t1>3，有

接下來令

tn+1=tn+21-n，(n≥1)，則對任意i≥1，ti∈

[t1,t1+2)。

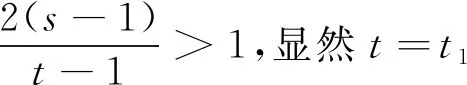
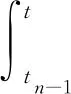
由數學歸納法可知，對任意t∈[tn,t1+2)有F(t)≥2n。

又對任意時間t∈[t1,+∞)，函數F(t)為光滑的，故

矛盾，綜上定理4得證。

4 應用

應用定理4并結合不同的Ricci孤立子方程條件，本節將主要采用定理2的結果對梯度擴張Ricci孤立子的勢函數估計進行證明并簡要介紹穩定及收縮Ricci孤立子的情況。

對于梯度擴張Ricci孤立子，張珠洪[13]已給出其勢函數上下界估計的相關結果，本節我們將結合Bakry-Emery Ricci張量及定理4的結論采用不同的方法給出其勢函數的一個下界估計。

定理5令(Mn,gij,f)為一個具有非負Ricci曲率的完備非緊致擴張梯度Ricci孤立子，孤立子方程滿足

則其勢函數f滿足估計：

式中：r(x)=d(x,p)為點x到固定點p∈M的距離函數；C為僅取決于維數n及單位球Bp(1)的度量gij的常數。更準確的說，常數C滿足

固定點p∈M及單位速度射線γ(t)，由Riccati 不等式可得

特殊的，當Ricf=-λg，則任意時間t>1滿足

-λ(t-1)-m(1)+[▽f,γ′]。

令C1=λ-m(1)+[▽f,γ′](1)，上述不等式為

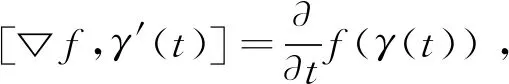
由定理假設勢函數

顯然有

代入上式得

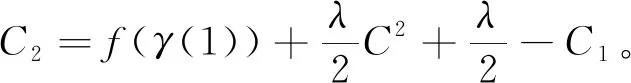
存在t1>3，對任意t≥t1，令常數C滿足

有

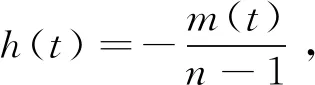
接下來的證明同定理4，可得矛盾，即證明了當勢函數滿足上界估計

時定理4也成立。

作為應用，令

故對于非緊致擴張梯度Ricci孤立子，存在僅取決于維數及黎曼度量的常數C使得

綜上定理得證。

注：上述定理推廣到非緊致穩定梯度Ricci孤立子可得其勢函數的一個上界估計。準確地說，若假設Bakry-Emery Ricci張量Ricf≥0，勢函數f(x)≤-C(r(x)+1),則存在常數C,當C≥6n-[▽f,γ′](1)-m(1)時，定理1成立。

特別地，Ricf=0(即(Mn,gij,f)為穩定Ricci孤立子)，自然可以證明曹懷東等[11]給出的經典的勢函數估計結果。

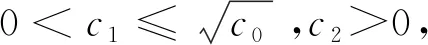
式中r(x)=d(x0,x)為點x到固定點x0∈M的距離函數，常數c0=Rmax滿足R+|▽f|2=c0。

此外，由定理1的證明顯然有如下推論。

推論2完備黎曼流形M若滿足Ricf≥0及f(x)≤-Cd2(x,p)，常數C>0，則M為緊致的。