通過類比和辨析培養學生的核心素養
——以“電磁感應的綜合應用”為例
張俊鋒
(廣東省河源市河源高級中學,廣東 河源 517500)
筆者在高三第二輪教學中,發現學生對某些知識掌握得過于碎片化、模型歸類混淆不清、在知識網絡上也總是短斤缺兩,導致很難使相關知識在新情境中得到應用.分析其根本原因,在于不能有效區分相近模型、不會從繁冗的知識中做減法,從本質上去理解相關知識點,無法形成更加具體的知識網絡,自然也很難形成核心素養和關鍵能力.筆者以“電磁感應的綜合應用”為例,一題多問,探索通過類比和辨析更好地促進二輪復習的有效教學.
題干情境:如圖1所示,固定在水平面上間距為l的兩條平行光滑金屬導軌,垂直于導軌放置的兩根金屬棒MN和PQ長度也為l、電阻均為R,兩棒與導軌始終接觸良好.MN兩端通過開關S與電阻為R的N匝金屬線圈相連,線圈的半圓內存在豎直向下均勻增加的磁場,磁感應強度的變化率為常量k.圖中虛線右側有垂直于導軌平面向下的勻強磁場,磁感應強度大小為B.金屬棒MN和PQ的質量均為m,若線圈半徑為r,金屬導軌足夠長、電阻忽略不計.
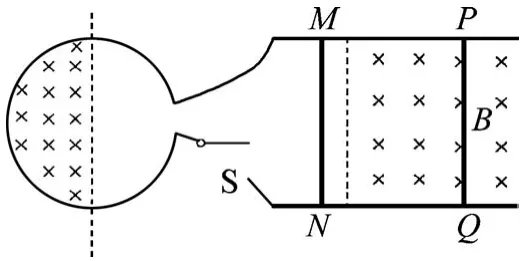
圖1
選題意圖:主要參照了2019年天津卷的第13題(如圖2所示),此題涉及的知識面較廣,非常適合進行知識的歸納和類比.為了教學的需要,筆者在原來的基礎上進行了改編,比如把線圈的匝數改編成N匝、磁場穿過的面積改編成原來的一半等,同時設置了更加多的綜合問題,比如對產生感應電動勢方式的變化、雙桿軌道的變化以及圖像的賞析與應用等.
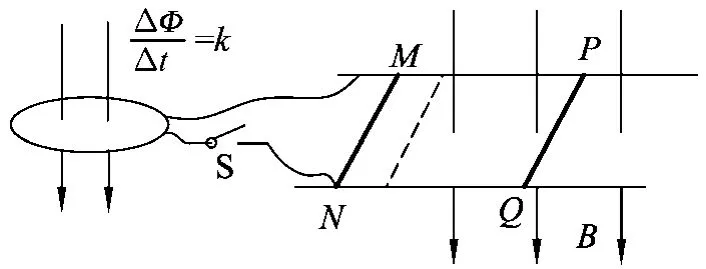
圖2
1 3種產生感應電動勢方式的類比和辨析
問題1.閉合S,當線圈中的磁場也為B時,若使線圈、導體棒PQ都保持靜止,需在其上分別施加多大的水平恒力?

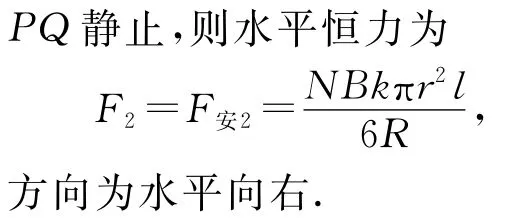
設計意圖:把磁場穿過的面積設計成一半,目的是要讓學生準確理解有效面積的真正意義;把線圈的匝數換成N匝,目的是要讓學生在計算安培力時應考慮線圈的匝數,這是學生最容易出錯的地方;分別求線圈、PQ所受的安培力,目的提醒學生計算時要注意電磁感應中的電路問題.
問題2.斷開S,PQ在上述恒力作用下,由靜止開始到速度大小為v的加速過程中流過PQ的電荷量為q,求該過程中回路產生的熱量Q1.
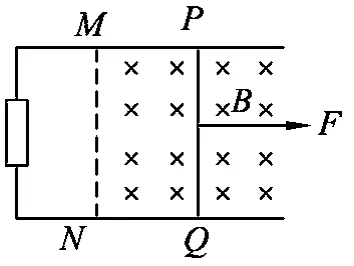
圖3

設計意圖:斷開S后,PQ在恒力F2施加后開始平動切割磁感線,屬于單桿切割問題.題目中引入電荷量q,是因為導體棒做變加速直線運動,通過流過導體棒的電荷量來求導體棒所發生的位移是非常重要的“技巧”,也是學生不易掌握的難點.
問題3.若將上題中線圈改成如圖4所示的雙圓線圈,線圈電阻不計.導體棒以O點為圓心以角速度ω在兩圓上轉動,其中大圓半徑為r、小圓半徑為,導體棒的電阻為R.閉合S,PQ在外力作用下仍保持靜止,求t時間內PQ上產生的熱量Q2以及通過PQ的電荷量q3.
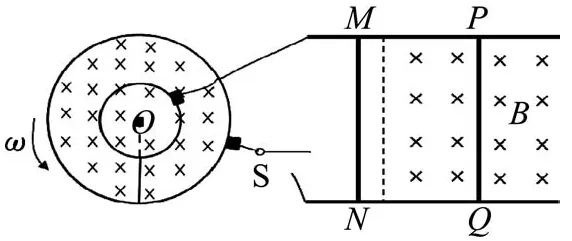
圖4
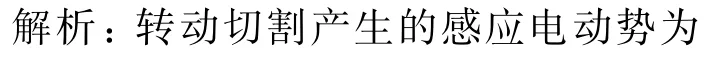

設計意圖:將上題中線圈改成如圖4所示的雙圓線圈,導體棒的轉動切割磁感線,屬于轉動切割問題.提醒學生注意并不是轉動切割的通式,而是E=Blˉv(ˉv是導體棒上各點速度的平均值).但又由于v=ωl,v與l是線性關系,故有(也可以通過v-t圖像類比來講解).從而可以推導出,這也是學生非常容易出現錯誤的地方.
綜上所述,3種產生感應電動勢的求法不同,各自的求法在一起類比和辨析更容易讓學生的知識網絡更加完整、認知也不易出現混淆;若電流恒定,求焦耳熱、電荷量時通常用Q=I2Rt、q=It,單桿的非勻速運動產生的電流不恒定,求焦耳熱時通常就要用到重要的功能關系Q=-W安(回路中產生的焦耳熱等于單桿克服安培力的功)、.通過類比和辨析,讓學生更完整地掌握電磁感應中焦耳熱以及通過導體棒電荷量的求解方法,才能讓學生在新情境下更好地選擇合適的求解方法,這樣才更加有利地培養學生的核心素養.
2 兩類雙桿問題的類比和辨析
問題4.斷開S,突然給MN一個初動量p,求PQ能產生最多的熱量Q1以及流過PQ的電荷量為q1.
解析:斷開S后,研究模型等效于圖5.
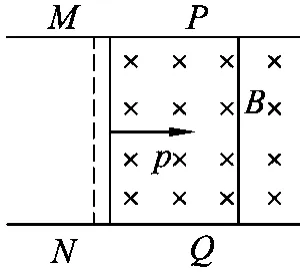
圖5
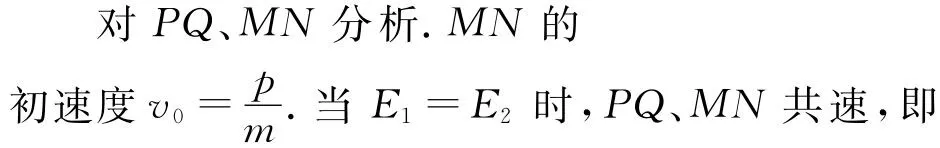

設計意圖:若MN獲得初動量就會進入磁場,與PQ共同切磁感線,屬于雙桿平動切割的典型問題.這跟木塊在木板上滑行(地面光滑)的模型類型的求解處理方法是類似的.通過跟以前模型的類比和辨析,有利于幫助學生對知識的整合以及升華,有利于學生對運動觀、能量觀等物理觀念的普適性有更清晰的認識.學生對雙桿下只對單桿用動量定理求通過電荷量的問題會比較疑惑,評講時亦可通過對導體棒MN進行動量定理,得出的結果是一致.通過兩種方法的類比和辨析,從而更加深刻理解通過串聯兩導體棒的電荷量.
問題5:若將上題中的導軌改成如圖6所示的導軌,且兩邊的導軌足夠長.PQ的長度、電阻和質量分別為l、R和m,MN的長度、電阻和質量分別為3l、3R和3m.斷開S,突然給MN一個初速度v0,求PQ能產生最多的熱量Q2以及流過PQ的電荷量為q2.
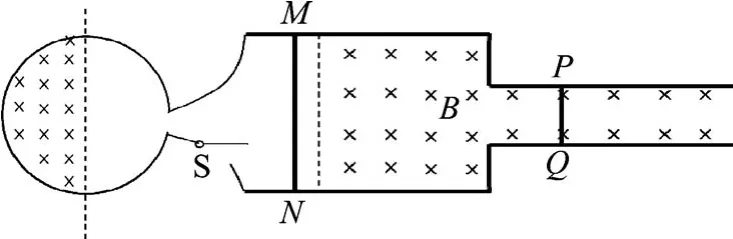
圖6


設計意圖:通過改變導軌的寬度后,很多學生容易認為兩導體棒的最終狀態依然共速,說明學生對知識本質的理解仍然不夠到位,準確的理解應該是兩導體棒所產生的感生電流等大反向,即有E1=E2;另外,不是等長的雙桿所受安培力的沖量不能抵消,所以不能用動量守恒定律求解,這也是學生很容易犯的錯誤.
綜上所述,兩類雙桿問題的核心在于對最終狀態的理解以及動量是否守恒的判斷,動量不守恒時應利用動量定理聯立求解.若沒有兩類雙桿問題放在一起進行類比和辨析,學生很容易以偏概全、分不清現象和本質,自然不能形成正確的物理觀念,更加不可能在新情境下應用,形成解決問題的根本能力.
總之,通過類比和辨析更加有利培養學生的核心素養,使學生掌握解決問題的關鍵能力,這既符合新課程標準的課程目標,又符合高考評價體系對學科核心素養的考查.

