中小跨徑斜拉橋拉索監(jiān)測方案研究

魏順波

[林同棪國際工程咨詢（中國）有限公司武漢分公司，湖北 武漢 430020]

0 引言

斜拉橋主要由索塔、主梁、斜拉索組成。斜拉橋是將主梁采用拉索錨固于橋塔上的一種結(jié)構(gòu)形式，是由承壓的塔、承彎的梁、受拉的索組合而成的結(jié)構(gòu)體系。斜拉橋是用拉索取代橋墩支承的多跨彈性支承連續(xù)梁，其中拉索是斜拉橋的重要受力部件。為了保證橋梁的安全性，技術(shù)人員對(duì)拉索安全性評(píng)估作了較多研究。

由于中小跨徑斜拉橋受到建設(shè)環(huán)境及經(jīng)濟(jì)條件的影響，一般未設(shè)置或只能在部分拉索上布置少量的傳感設(shè)施來監(jiān)測橋梁拉索的安全。如何將少量傳感設(shè)施布置在橋梁拉索的恰當(dāng)位置并取得最接近實(shí)際情況的數(shù)據(jù)就成為橋梁安全監(jiān)測設(shè)計(jì)時(shí)需要處理的關(guān)鍵性問題之一，而恰當(dāng)?shù)奈恢弥荒芡ㄟ^拉索的相關(guān)性來確定[1]，這也是本文研究的主要內(nèi)容。

本文以武漢市光谷八路跨外環(huán)橋梁工程為背景，研究拉索之間的相關(guān)性，尋求最優(yōu)拉索組合作為關(guān)聯(lián)拉索，盡可能地反映橋梁的整體索力狀態(tài)。

1 工程概況

武漢市光谷八路跨外環(huán)橋梁工程上部結(jié)構(gòu)跨徑布置為：2×30m（預(yù)應(yīng)力混凝土連續(xù)箱梁）+（80+50）m（鋼箱梁斜拉橋）+3×30m（預(yù)應(yīng)力混凝土連續(xù)箱梁）+3×30m（預(yù)應(yīng)力混凝土連續(xù)箱梁）。下部結(jié)構(gòu)橋墩采用T形墩，橋塔采用“人”字形獨(dú)塔，橋臺(tái)采用樁柱式橋臺(tái)。該橋主橋?yàn)榈湫偷乃鬏o梁結(jié)構(gòu)體系。

基于Midas/Civil建立光谷八路橋主橋有限元模型（見圖1），其中拉索編號(hào)奇數(shù)項(xiàng)為80m跨側(cè)，偶數(shù)項(xiàng)為50m跨側(cè)，由橋塔向兩側(cè)依次編號(hào)。對(duì)計(jì)算模型采用依次斷開1根拉索，得到其他拉索的索力變化量，從而對(duì)計(jì)算所得的所有數(shù)據(jù)采用關(guān)聯(lián)性分析，得到相關(guān)拉索的影響大小關(guān)系。

圖1 光谷八路橋主橋有限元模型

2 數(shù)據(jù)分析

按照橋梁已有的設(shè)計(jì)參數(shù)，可以計(jì)算出本橋22根斜拉索在標(biāo)準(zhǔn)組合下的成橋索力，見表1。

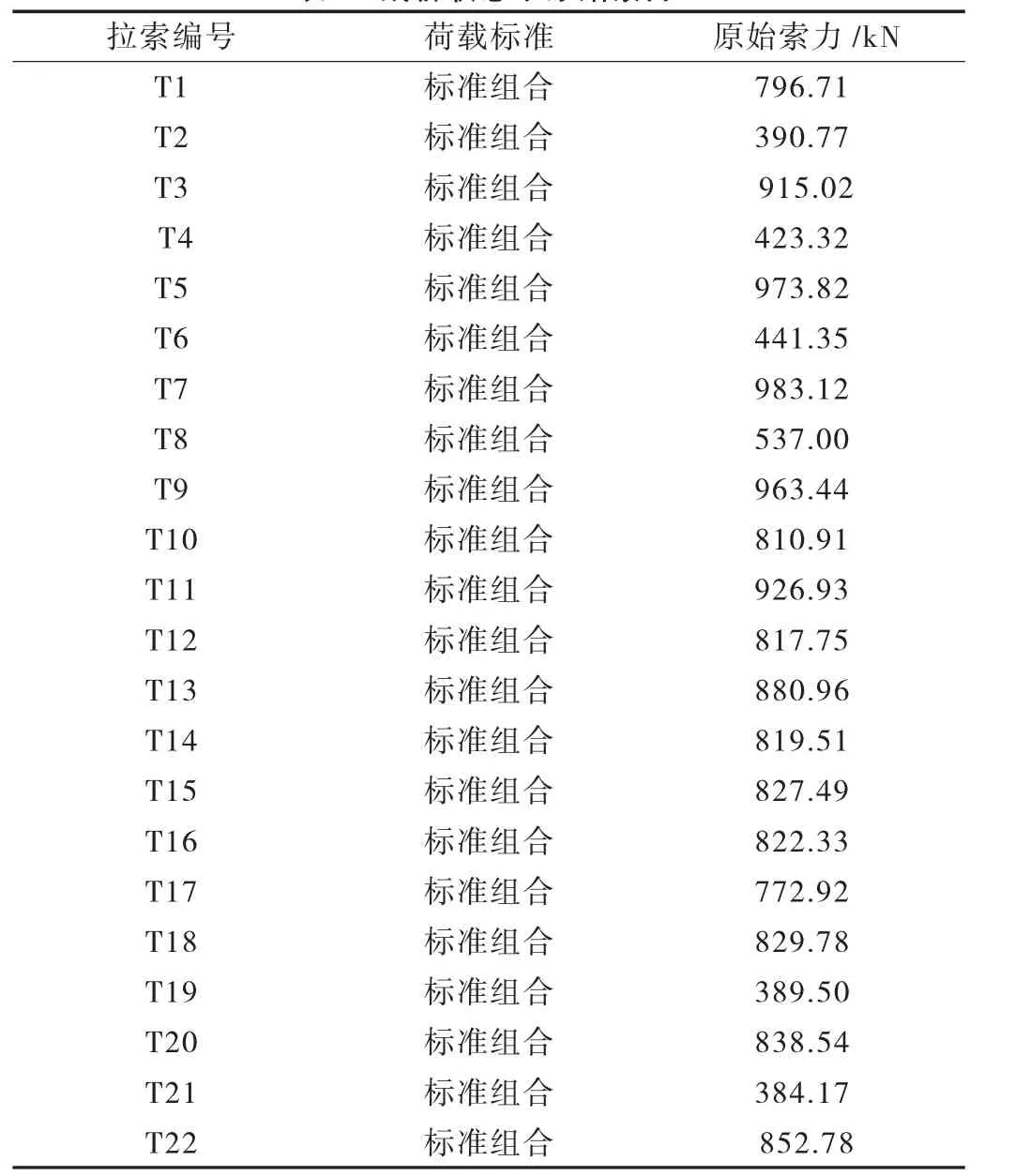
表1 成橋狀態(tài)下原始索力

將成橋時(shí)的狀態(tài)作為第1施工階段，然后依次鈍化需要考慮斷開的拉索作為第2施工階段，以此為原則，依次設(shè)定斷開拉索為各自的施工階段，從而計(jì)算出在相同的原始索力下，依次斷開每根拉索而導(dǎo)致的其他拉索索力變化。

由于計(jì)算數(shù)據(jù)較多，難以分析其規(guī)律性，現(xiàn)選取斷開拉索T1和T12為例，分析其余拉索的索力變化特點(diǎn)。

斷開拉索T1后，其余拉索的索力變化見圖2；斷開拉索T12后，其余拉索的索力變化見圖3。

由圖2、圖3可知，在斷開單根拉索時(shí)，其同側(cè)拉索索力變化較大，另一側(cè)拉索索力變化較小。因此本文將22根拉索分成2組，假定80m跨拉索為A，50m跨拉索為B，由橋塔向兩側(cè)依次重新編號(hào)，并進(jìn)行相關(guān)性研究。考慮到每根拉索的原始索力不同，因此采用索力變化量/索力原始量，即索力變化率來優(yōu)化處理計(jì)算數(shù)據(jù)。根據(jù)優(yōu)化處理計(jì)算數(shù)據(jù)可以得知，斷開某根拉索后，與其相近的索力變化率較大，隨著距離增大，索力變化率基本呈現(xiàn)下降趨勢（個(gè)別拉索如A10、B3、B4的索力變化率不符合此規(guī)律是因?yàn)槠涑跏妓髁^相鄰拉索索力差值過大，導(dǎo)致部分拉索斷裂后，計(jì)算得到的索力變化率偏大）。

圖2 斷開拉索T1后其余拉索的索力變化

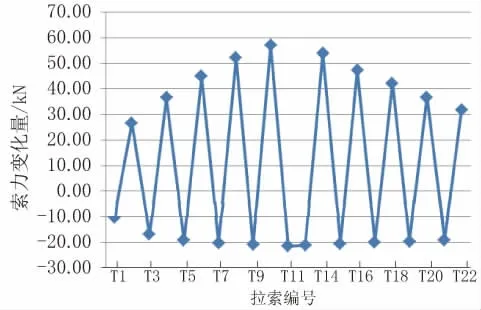
圖3 斷開拉索T12后其余拉索的索力變化

3 基于拉索關(guān)聯(lián)影響矩陣的研究

因?yàn)榈玫降臄?shù)據(jù)都相近，難以直接判斷拉索與拉索的相關(guān)性大小。為方便研究，本文采取設(shè)定閥值的方式，假定僅考慮閥值以內(nèi)的拉索與斷開拉索關(guān)聯(lián)，閥值之外的拉索無需與斷開拉索相關(guān)聯(lián)。通過多方面對(duì)比，確定以索力變化率范圍的均值作為閥值來篩選相應(yīng)拉索，研究其與斷開拉索之間的關(guān)聯(lián)性[1]。以斷開拉索A3為例，其造成同側(cè)其他10根拉索索力變化率的平均值為0.0516，則索力變化率大于這個(gè)閥值的拉索A1、A2、A4、A5、A6被認(rèn)為是與拉索A3相關(guān)。

按照此方法，將存在相關(guān)性的記為1，認(rèn)為不用考慮相關(guān)性的記為0，可得出22根拉索之間的關(guān)聯(lián)矩陣。

因此，可選擇拉索A1、A4、A7、A11這4根作為80m跨的關(guān)聯(lián)拉索，B1、B5、B8、B11這4根作為50m跨的關(guān)聯(lián)拉索，通過在這8根拉索上布置傳感器來反映整體拉索的索力狀況，保證經(jīng)濟(jì)性和實(shí)用性。

說明：（1）選擇關(guān)聯(lián)拉索已將個(gè)別拉索索力變化率規(guī)律不符合總體趨勢的剔除；（2）部分3根拉索也可以反映整體的關(guān)聯(lián)性，但考慮到這種方式下數(shù)據(jù)過少且分散，數(shù)值擬合時(shí)無法得到準(zhǔn)確的線性關(guān)系，故不作考慮。

4 基于關(guān)聯(lián)性的拉索狀態(tài)評(píng)估

為驗(yàn)證4根關(guān)聯(lián)拉索的最優(yōu)性，將選擇80m跨的A1、A3、A5、A7、A9共5根拉索作為關(guān)聯(lián)拉索與之對(duì)比。以斷開拉索A2為例，分析4根、5根這2種關(guān)聯(lián)拉索組合下索力狀態(tài)評(píng)估的準(zhǔn)確性。由于計(jì)算數(shù)據(jù)有限，為減小誤差，借助Matlab數(shù)值分析軟件，采用最小二乘法擬合3次曲線方程。

4.1 5根關(guān)聯(lián)拉索

模擬斷開拉索A2，可得到測點(diǎn)拉索（5根）的索力變化率，見表2。

表2 斷開拉索A2后測點(diǎn)拉索（5根）的索力變化率

擬合得到的曲線方程為：

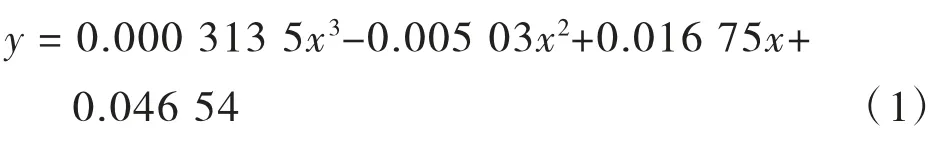
如圖4所示，y取最大值時(shí)，x=2.0628，故可判斷是拉索A2斷裂。

圖4 斷開拉索A2后測點(diǎn)拉索索力（5根）的關(guān)聯(lián)值

4.2 4根關(guān)聯(lián)拉索

模擬斷開拉索A2，可得到測點(diǎn)拉索（4根）的索力變化率，見表3。

表3 斷開拉索A2后測點(diǎn)拉索(4根)的索力變化率

擬合得到的曲線方程為：

如圖5所示，y取最大值時(shí)，x=1.6142，故可判斷是拉索A2斷裂。

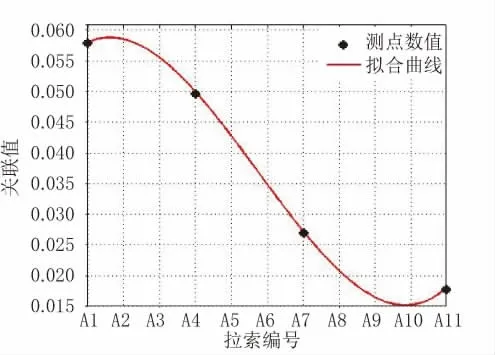
圖5 斷開拉索A2后測點(diǎn)拉索索力（4根）的關(guān)聯(lián)值

綜合2個(gè)結(jié)果可以看出，80m跨在2種關(guān)聯(lián)拉索狀態(tài)下，都可以評(píng)估拉索A2的索力狀態(tài)。在考慮經(jīng)濟(jì)成本后，優(yōu)先選擇A1、A4、A7、A11這4根作為關(guān)聯(lián)拉索，并模擬斷開拉索A3進(jìn)行驗(yàn)證。

模擬斷開拉索A3，得到測點(diǎn)拉索索力變化率，擬合得到的曲線方程為：

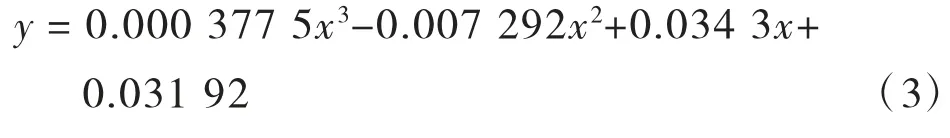
如圖6所示，y取最大值時(shí)，x=3.0964，可判斷是拉索A3斷裂。

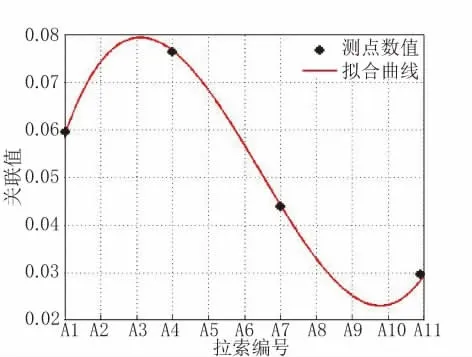
圖6 斷開拉索A3后測點(diǎn)拉索索力（4根）的關(guān)聯(lián)值

5 結(jié) 語

（1）通過計(jì)算模型模擬拉索斷開后，其余索力的變化情況來分析各根拉索之間的關(guān)聯(lián)性大小，選出能反映全橋索力狀態(tài)的最優(yōu)拉索組合，布設(shè)傳感器，再根據(jù)監(jiān)測數(shù)據(jù)評(píng)估拉索狀態(tài)，既可保證橋梁結(jié)構(gòu)安全，同時(shí)也可節(jié)約監(jiān)測成本。

（2）本文所選工程中部分拉索原始索力相比其他拉索差距較大，導(dǎo)致采用索力變化率的方式不能全面反映所有索力之間的相關(guān)性，可能與現(xiàn)實(shí)情況存在誤差。

（3）根據(jù)索力的變化規(guī)律可以知道，并非所有拉索都能通過擬合3次曲線計(jì)算其最大值來作為評(píng)估手段的。

（4）本文在處理數(shù)據(jù)時(shí)采用的索力變化量與原始索力之比，可能會(huì)導(dǎo)致得出的相關(guān)性誤差較大，后期將考慮灰色關(guān)聯(lián)度和神經(jīng)網(wǎng)絡(luò)算法，來優(yōu)化拉索之間的相關(guān)性。

（5）本文僅考慮了單根拉索斷開時(shí)的關(guān)聯(lián)性，并且只有理論計(jì)算數(shù)據(jù)，暫無實(shí)測數(shù)據(jù)進(jìn)行驗(yàn)證。

（6）本文所選的實(shí)際工程為獨(dú)塔單索面索輔體系，所得結(jié)論沒有普遍性，對(duì)于雙塔雙索面和獨(dú)塔雙索面沒有進(jìn)行對(duì)比分析。