2021年新高考Ⅰ卷第21題的溯源與推廣

高繼浩

(四川省名山中學 625100)

1 試題再現

(1)求C的方程；

2 教材溯源

高中數學教材是高考數學命題的藍本,上述題目1源于人教A版高中數學教材選修4-4第38頁的例題.

題目2 如圖1所示,AB,CD是中心為點O的橢圓的兩條相交弦,交點為P.兩弦AB,CD與橢圓長軸的夾角分別為∠1,∠2,且∠1=∠2.

求證：|PA|·|PB|=|PC|·|PD|.

圖1

題目1是已知線段長度關系求兩線斜率關系,題目2是已知角度關系(建系后即為兩線傾斜角或斜率關系)找線段長度關系.教材上緊接此題有一探究：如果把橢圓改為雙曲線,是否會有類似的結論？題目1考查的正是雙曲線的情形.因此,平時教學應用好教材,學透教材,高三復習時更應回歸教材.

3 結論推廣

由特殊到一般可以很好地培養和提升邏輯推理、數學抽象和直觀想象等數學核心素養.試題中曲線C為雙曲線的一支,對其進行一般化推廣,我們得到：

代入雙曲線方程整理，得

則b2cos2α-a2sin2α≠0,且此關于t的一元二次方程有兩個根,設這兩個根分別為t1,t2,則

|TA|·|TB|=|t1|·|t2|=|t1t2|

由T與A,B和P,Q的位置關系知

故|TA|·|TB|=|TP|·|TQ|

?b2cos2α-a2sin2α=b2cos2β-a2sin2β

?b2cos2α+a2cos2α=b2cos2β+a2cos2β

?cos2α=cos2β

?cosα=-cosβ

?α+β=π.

故|TA|·|TB|=|TP|·|TQ|

?b2cos2α-a2sin2α=a2sin2β-b2cos2β

?b2(cos2α+cos2β)=a2(sin2α+sin2β)

取消結論1中“同一支”的條件限制,由以上證明過程可知：

在橢圓中有：

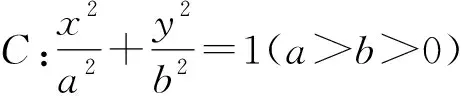
結論3、結論4的證明過程與結論1、結論2類似，此處略.

在拋物線中有：

結論5 過不在拋物線C:y2=2px(p>0)上的一點T作兩條直線,分別交拋物線C于A,B兩點和P,Q兩點,直線AB與直線PQ的傾斜角分別為α,β,則|TA|·|TB|=|TP|·|TQ|的充要條件是α+β=π.

則sin2α≠0,且此關于t的一元二次方程有兩個根,設這兩個根分別為t1,t2,則

|TA|·|TB|=|t1|·|t2|=|t1t2|

同理可得

故|TA|·|TB|=|TP|·|TQ|

?sin2α=sin2β

?sinα=sinβ

?α+β=π.