基于深度強化學習算法的財務機器人任務分配的研究

劉 星，張文娟，廖帥元

（1.國網湖南省電力有限公司 信息通信分公司，長沙 410007；2.長沙凱鈿軟件有限公司，長沙 410000）

0 引言

任務分配的主要研究方法可分為兩種：固定分配方法和綜合評估方法。固定分配方法：按要求設置好每個任務的執行用戶。該方法存在一定缺陷，即不能隨著系統和實際任務的變化而靈活設置任務的執行用戶。綜合評估方法：通過考慮各方面因素，綜合評估每個時刻可能發生的不同情況和影響因子（如負載、工作能力水平等），以此進行任務分配。財務機器人采用綜合評估的思想，以工作任務進度自動計算規則作為深度策略梯度方法的重要依據，得到最大的總獎賞。

近年來，深度學習、強化學習是機器學習領域的一個研究熱點，應用廣泛。深度學習側重對事物的感知，強化學習更側重解決問題，因此采用深度學習算法以及自定義策略梯度優化任務執行路徑，為任務分配提供新的思路，從而找到全局最優解。

1 任務分配數學模型

1.1 問題描述

目前輸配電成本監審日常工作仍舊采用人工方式進行工作安排、電話溝通、紙質傳遞和報送等工作，缺少對整體工作計劃的有效管理手段，工作范圍上存在遺漏缺少情況，工作進度上無法及時準確地把控和監管，工作過程中信息傳遞和溝通不暢通，部門工作配合方面步伐不一致，工作的組織和開展零散、效率不高，工作成果的質量低，亟待建設相應的信息化項目來滿足實際成本監審和監管的工作需要，做到工作事前有計劃、事中有監管（進度和質量）、事后有評價，提升精益管理水平。

在財務機器人工作分配中通常包括人工分配任務以及自動分配任務。在任務分配過程中，由于系統缺少對用戶工作經驗、用戶任務完成度的評估，而引起任務分配不均衡。這種情況通常會降低工作效率。因此任務均衡分配極其重要。

1.2 任務分配的主要因素

在財務機器人中，任務和用戶及其任務完成情況是任務分配的核心影響因素。由于每個任務和用戶都存在不同的屬性值，因此在財務機器人工作任務分配問題中，依據主要的工作任務進度自動計算規則判定該用戶是否是最合理的任務執行者。

工作任務進度自動計算規則是由開發者根據以往的工作經驗，合理得到的一組判定任務完成進度的算法。進度自動計算結果=A*B*C,其中B 和C 支持自定義。其中A 表示任務提交次數，如表1；B 表示任務收集狀態，如表2；C 表示任務審核狀態，如表3。

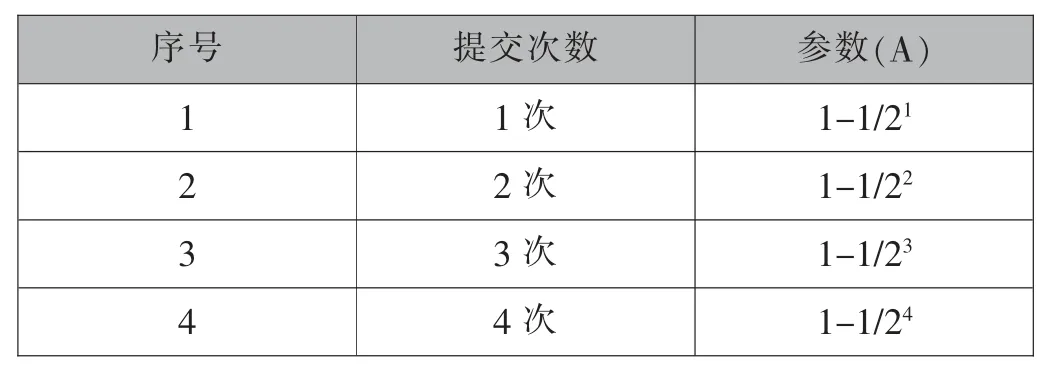
表1 提交次數

表2 收集狀態

表3 審核狀態

為了提高財務機器人的工作效率，達到最高點，需構造工作任務進度自動計算規則，讓任務分配均衡達到最好，因此構造任務分配總體達到最優目標函數是必要的。

2 算法分析

深度強化學習（Deep Reinforcement Learning，DRL）是人工智能領域新的研究熱點，DRL 是由具有感知能力的深度學習（Deep Learning，DL）和具有決策能力的強化學習（Reinforcement Learning，RL）相結合產生的。DL 的基本思想是通過多層的網絡結構和非線性變換，組合底層特征，形成抽象的、易于區分的高層表示，已發現數據的分布式特征表示。RL 的基本思想是通過最大化智能體（Agent）從環境中獲得的累計獎賞值，以學習到完成目標的最優策略。其中DQN 作為經典算法之一，它用一個深度網絡代表價值函數，依據強化學習中的Q－Learning，為深度網絡提供目標值，對網絡不斷更新直至收斂。由于DQN 是基于Q－Learning，如果輸出DQN 的Q 值，可能會發現，Q 值非常大，這時QLearning 預測目標值的時候可能出現overestimate，對于這一類問題，我們可采用DDQN 解決。

本文采用DQN 算法、DDQN 和輪詢調度三種算法，其中DQN 和DDQN 融合了強化學習的Q－Learning和深度神經網絡，本文將探索哪一種算法能更快地求取合理的任務分配。

2.1 DQN 算法

DQN 包含狀態（state）、行動（action）和獎勵（reward）三個要素。reward 值靜態描述了各個狀態之間轉移的立即獎勵值，行動則決定狀態之間的轉移規則。QLearning 迭代時采用立即獎勵值、Q 值函數和折扣率共同組成評價函數，Q 值表中保存各狀態行動對（s，a）的估計值。Q－Learning 算法在給定策略h（x）下，在狀態S采取行動A的評價函數為：

式中：α∈（0，1）為學習步長；γ∈（0，1］為折扣率，決定agent 以多大權重考慮未來獎勵；t 為時間步；R為在采取當前（S，A）的立即獎勵；max 函數表示算法會根據下一個（S，A）中預測值的最大值來評價（S，A）；式中R＋γ max Q（S，a）－Q（S，A）定義為時間差分誤差（TD error），算法通過TD error 對估計值遞增更新直到收斂，行動選擇常采用ε－greedy 策略。將agent從開始狀態轉移到目標狀態整個過程稱為一次情景（epsiode），在episode 中每次狀態轉移的時刻稱為一個時間步（time step）。

Deep Q－Learning 算法流程如下：

（1）首先初始化“樣本集”（Memory D），簡稱D，它的容量為N，初始化Q 網絡，隨機生成權重ω，初始化target Q 網絡，權重為ω-=ω，循環遍歷episode=1，2，…，M：初始化initial state S1；

（2）循環遍歷step=1，2，…，T：用∈-greedy 策略生成action at（以∈概率選擇一個隨機的action，或選擇at=maxaQ（S，a；ω））；

（3）執行action at，接收reward rt 及新的state S＋1；

（4）將transition 樣本（S，a，r，S）存入D 中；

（5）從D 中隨機抽取一個minibatch 的transitions（S，a，r，S）；

（6）如果j＋1 步是terminal 的話，令y=r；否則，令y=r＋γ maxa′Q（S，a′；ω-）；

（7）對（y-Q（S，a；ω））2 關于ω 使用梯度下降法進行更新；

（8）每隔C steps 更新target Q 網絡，ω-=ω。

（9）輸出原始問題的最優策略h*（x）為在各狀態下貪婪地選擇Q 值最大的行動。

2.2 DDQN 算法

DDQN 網絡結構和DQN 一樣，也有一樣的兩個Q網絡結構。在DQN 的基礎上，通過解耦目標Q 值動作的選擇和目標Q 值的計算這兩步，來消除過度估計的問題。在DDQN 這里，不是直接在目標Q 網絡里面找各個動作中最大Q 值，而是先在當前Q 網絡中先找出最大Q 值對應的動作，即

然后利用這個選擇出來的動作amax（S，w）在目標網絡里面去計算目標Q 值。即：

綜合起來寫就是：

DDQN 算法流程如下：

（1）隨機初始化所有的狀態和動作對應的價值Q，且隨機初始化當前Q 網絡的所有參數w，初始化目標Q 網絡Q′的參數w′=w。清空經驗回放集合D。

（2）進行迭代。

1）初始化S 為當前狀態序列的第一個狀態，拿到其特征向量φ（S）；

2）在Q 網絡中使用φ（S）作為輸入，得到Q 網絡的所有動作對應的Q 值輸出。用∈-貪婪法在當前Q 值輸出中選擇對應的動作A；

4）將｛φ（S），A，R，φ（S′），is_end｝這個五元組存入經驗回放集合D；

5）S=S′；

6）從經驗回放集合D 中采樣m 個樣本｛？（S），A，R，φ（S′），is_endj｝，j=1，2，…，m，計算當前目標Q 值y：

7）使用均方差損失函數1／m∑j=1／m（y-Q（φ（S），A，w））2，通過神經網絡的梯度反向傳播來更新Q 網絡的所有參數w；

8）如果T%C=1，則更新目標Q 網絡參數w′=w；

9）如果S′是終止狀態，當前輪迭代完畢，否則轉到步驟2）。

2.3 輪詢調度算法

輪詢調度算法是簡潔的，無須記錄所有用戶任務分配情況，只需要把任務依次按順序輪流分配給用戶，當用戶都分配了任務后，還需要繼續分配，則重新開始循環。

3 任務分配流程

（1）學習環境設計：通過和環境進行交互，利用不確定的環境獎賞來發現最優行為序列。本文提出的學習環境主要根據調度方案包含工作任務進度完成度建模，獲取當前調度方案下完成任務所需的時間，從而對當前調度方案針對調度目標的優劣進行評估。

（2）動作集：動作集是為Q 學習算法的可以選擇執行動作的集合。本文通過工作任務自動計算規則，充當Q 學習算法的動作集合。

（3）狀態變量確定和狀態空間劃分：該因素是Q 學習算法合理選擇動作的基礎，為了使得算法更好地選擇工作任務自動計算規則，實現優化調度目標，必須完成算法狀態空間的離散化和定量化。

（4）懲罰函數：懲罰函數的設計目的在于對算法每次動作執行后的優化效果進行獎懲。對于優化的動作，進行獎勵，使得該動作具有較大的選取概率；對于不優的動作，進行懲罰，減小該動作的選取概率。

（5）算法流程：根據上述Q 學習算法相關定義，最后確定算法的流程。

算法實現步驟如圖1 所示。

圖1 優化算法實現步驟

4 仿真校驗

為了驗證上述方法的均衡性以及工作效率，選擇本文提出的DQN 算法、DDQN 算法和輪詢調度方法進行實驗對比分析。

4.1 用戶所獲得各類任務比例

三種方法的用戶所獲得的類別任務比例分別如圖2、圖3、圖4 所示。從圖2 可以看出，對于不同的任務，4個實驗用戶分配到的任務數量基本一致，并沒有按照用戶完成任務的效率合理分配任務；從圖3 可以看出，根據不同的任務類型，4 個實驗用戶分配到的任務數量完全不一樣，可以推斷出DQN 算法可以給用戶合理地分配任務；從圖4 可以看出，DDQN 與DQN 任務分配占比相似，可推斷DDQN 算法可用于任務分配問題。用戶對于該任務完成度越高，被分配的任務量也就越多，并且隨著其他一些任務或用戶屬性的影響，任務量與工作進度之間的關系還可以產生動態變化，說明深度強化學習算法可以有效的按照工作進度合理分配任務。

圖2 輪詢調度法

圖3 DQN 算法

圖4 DDQN 算法

4.2 深度強化學習訓練結果分析

因為DQN 和DDQN 算法區別在于Q－target 的計算，所以兩者神經網絡結構一樣，結構圖如圖5 所示。其中target_net 與eval_net 采用相同的網絡架構和不同的參數。

圖5 神經網絡結構圖

采用DQN 算法得到的損失結果展示如圖6 所示。采用DDQN 算法得到的損失結果展示如圖7 所示。由圖可知隨著訓練步長的增加，損失值在不斷減小，表明該函數更加趨近于最優解。

圖6 DQN 函數損失圖

圖7 DDQN 函數損失圖

5 結論

本文通過系統地分析任務分配問題的特點，提出了財務機器人任務分配問題的數學描述，采用深度強化學習算法（DQN、DDQN）解決任務均衡分配問題。這兩種方法收斂速度快，可以有效地處理連續動作集的問題，彌補了后者初期解決速度慢的缺點。實驗結果表明，該方法適用于財務機器人，在性能上優于傳統的任務分配方法（輪詢調度法）。