基于改進SARIMA-LSTM的海上風速預測方法

余聰聰，熊才權，徐仕強，古小惠

(湖北工業大學計算機學院，湖北 武漢 430068)

風速不僅決定了船只的航行路線，還對船只的航行安全產生很大的影響。如果船只能夠在出海前比較精確的掌握未來一段時間相應海域的風速情況，那將對船只的航行線路規劃產生積極影響。

針對近海海域風速變化的特點，風速預報大多在一些臨近海邊的風場中。如張增海等[1]通過地表的粗糙度指數和大氣的穩定度給出了相應的海上風速和沿海風速觀測站風速關系的經驗公式，此經驗公式適用于該觀測站附近的海域風速預測。考慮到風速序列中既有線性因素的影響又有非線性因素的影響和單一預測模型自身的局限性，研究者們又提出來一系列組合預測的風速預測模型[2-4]。如田中大等[5]將ARIMA[6]和回聲狀態網絡(Echo State Network, ESN)相結合、李蓉蓉等[7]將時間序列分析和LSTM相結合，高桂革等[8]將經驗模態分解和極限學習機相結合，王耀慶等[9]將小波變換與LSTM相結合，他們的做法都是將原始風速序列分解為線性自相關和非線性殘差兩部分，使用組合模型分別對兩部分進行建模預測，充分利用好每一個模型優勢，提高風速預測[10]精度。

現有研究使用季節性差分移動自回歸平均模型(Seasonal Autoregressive Integrated Moving Average Model, SARIMA)進行時間序列預測時，對于季節性參數的判定大都是通過人為估計，存在一定的誤差。本文提出將STL[11](Seasonal-Trend decomposition procedure based on Loess)方法用于SARIMA模型季節性差分步長的判定，以提高 SARIMA的預測精度，進而提升和長短時記憶神經網絡模型(Long Short-term Memory，LSTM)相結合后對海上風速預測的準確性。實驗結果表明，通過對SARIMA模型的改進，可以有效提高海上風速預測的精度。

1 基礎算法

1.1 季節性差分自回歸移動平均

在眾多時間序列中，由于月度、季度等因素影響，如某景點的旅游人次數據，某些序列常常呈現出一種周期性變化，這類序列統稱為季節性序列，同時也衍生出了季節性 ARIMA 模型，用 SARIMA 表示，它對數據變量建立序列回歸，并根據數據周期項和隨機項對序列未來趨勢做測算。SARIMA 模型[12]源于 ARIMA 模型。將原始的時間序列記為yt，SARIMA模型首先是對yt進行差分處理，消除序列當中的趨勢性，然后通過季節性差分消除季節性，經過處理后，模型可以表示為SARIMA(p,d,q)(P，D，Q)s，記作[10]：

φp(Bs)φP(B)(1-Bs)D(1-B)dyt=

ΘQ(Bs)θq(B)at

(1)

其中：φp(BS)為季節P階自回歸算子多項式、p為自回歸階數、P為季節性自回歸階數、φp(B)為非季節自回歸多項式、D為季節差分階數、d為逐期差分階數、s為季節差分步長、(1-Bs)D為季節差分算子、(1-B)d為差分算子、Q為季節移動平均階數、ΘQ(Bs)為季節Q階移動平均算子多項式、θq(B)為非季節移動平均多項式、at為白噪聲序列。

1.2 循環神經網絡

典型循環神經網絡結構一般如圖1所示，主體結構的輸入包括輸入層xt，循環邊上所提供的上一時刻隱藏狀態st-1。在某一個時刻t，網絡在讀取了xt和st-1之后還會生成新的隱藏狀態st和產生當前時刻的輸出ot。

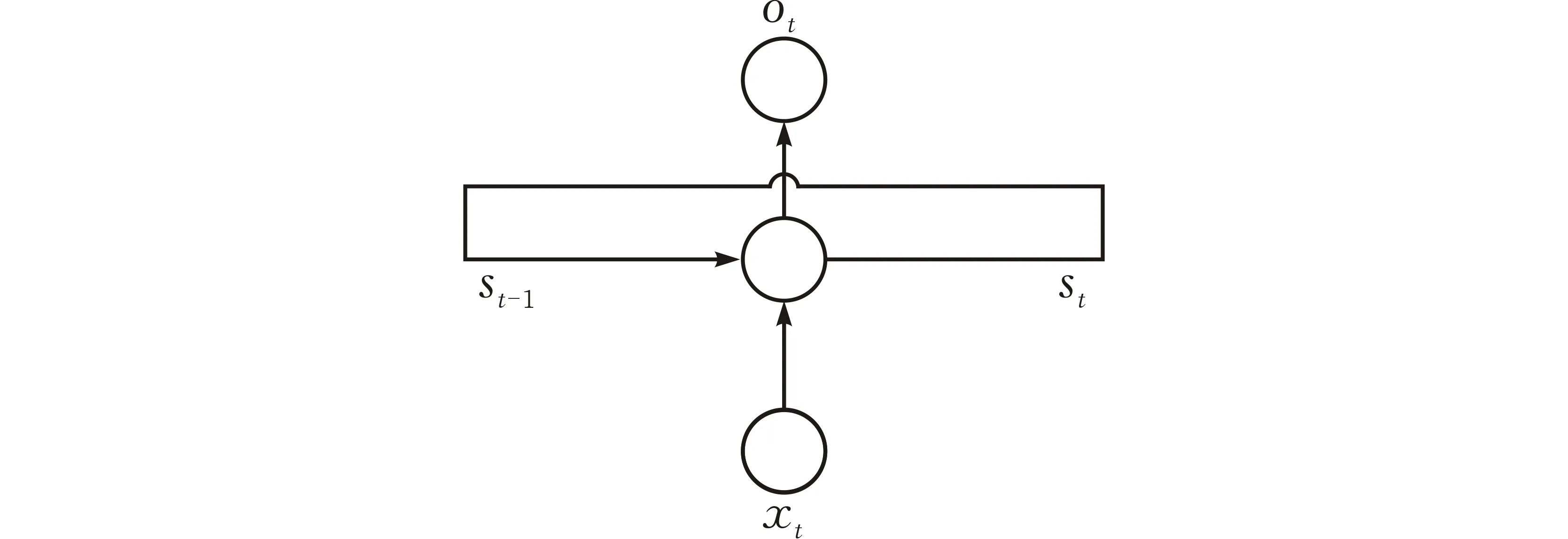
圖 1 循環神經網絡結構圖

從理論上來說，循環神經網絡可以處理任意長度的序列，但在實際的訓練過程中，當序列過長時，一方面可能會導致出現梯度消失和梯度爆炸的問題，另一方面網絡展開后會占用過大的內存，因此在實際使用時會規定一個序列的最大長度，當序列的長度超過這個長度時，應該進行分段處理。

1.3 LSTM神經網絡結構

循環神經網絡與傳統的神經網絡相比可以通過歷史保存的信息來輔助當前的決策，但在某些問題中，模型只需要短期的信息來處理當前任務，因此循環神經網絡存在長期依賴問題。長短時記憶神經網絡是一種特殊的循環神經網絡，與傳統的循環神經網絡相比，LSTM在其基礎上添加了一些“門”結構，它可以選擇性保留網絡信息，有效地解決了一些無效數據的依賴問題，提高了神經網絡的效率，LSTM單元結構如圖2所示。

圖 2 LSTM網絡結構圖

圖2中的“遺忘門”和“輸入門”是LSTM結構中最為核心的部分。其中“遺忘門”會依據當前輸入的xt和上一時刻輸出的ht-1來決定遺忘哪一部分記憶，而“輸入門”依據xt和ht-1決定哪些信息應該加入到狀態ct-1中從而生成新的狀態ct。此時“輸出門”會根據當前時刻的輸入xt，上一時刻的輸出ht-1和ct來決定此刻的輸出。

2 STL對SARIMA模型的改進

STL是一種通用穩健基于Loess的分解時間序列方法。估計某個響應變量值時，優先選擇預測變量附近的一個數據子集，通過采用二次回歸或加權最小二乘法進行線性回歸，使離該響應變量較遠點的權重變小后通過局部回歸模型估算出響應變量的值。它通過提取時間序列中的部分局部數據，從而使得回歸曲線變得平滑且讓數據在一定的范圍內的趨勢和變化規律變得更加明顯。影響海上風速序列變動的因素包括季節變動、趨勢變動和不規則變動，SARIMA模型季節性差分步長通常是人為估計，會存在誤差，使得模型的預測結果不準確。為了能夠更好的確定SARIMA模型的季節性差分步長，使用STL將海上風速序列進行分解，通過分解后的風速季節分量來確定該參數值。分解后的表達式可以表示如下：

Tt=St+Ct+Rt(t|0≤t≤|T|,t∈Z)

(2)

其中，T為原始海上風速序列、S為季節分量、C為趨勢分量、R為剩余分量、|T|為序列的長度。STL分解過程由內循環和外循環兩部分組成。每次內循環都包含季節性平滑，用來更新季節性分量，而外循環則是在內循環完成之后計算穩健的權重，以減少下一次內循環中異常值對更新季節性分量的影響。STL內循環過程見圖3。步驟分別為：

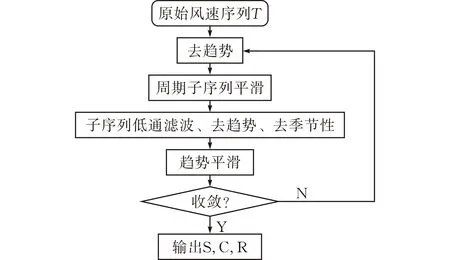
圖 3 STL內循環過程圖

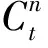
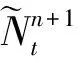
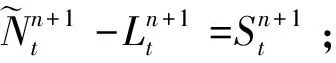
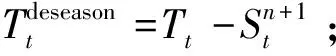
在外循環中，使用內循環得到的趨勢分量C和季節分量S來計算剩余分量S。分析季節分量S得到SARIMA模型的季節性差分步長。

3 改進后的SARIMA與LSTM組合模型的建立

海上風速序列不僅具有線性特征，還具有非線性、隨機性和非平穩性等特征。改進后的SARIMA模型對風速序列中的線性部分擬合得更好，而長短時記憶網絡模型(LSTM)的優勢在于擬合較為復雜的非線性，非平穩性數據，二者的優勢互補。假設存在風速時間序列Yt由兩部分組成，分別為線性自相關的Lt和非線性的殘差Nt，則有：Yt=Lt+Nt，本文將采用改進后的SARIMA和LSTM的組合模型進行風速預測。

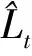
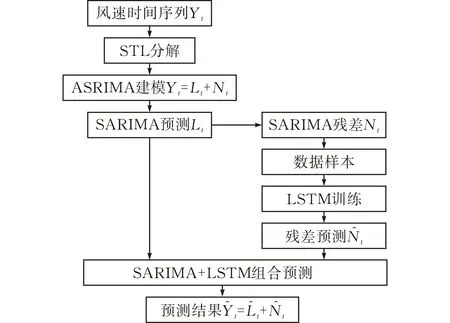
圖 4 SARIMA與LSTM組合預測原理圖

4 實驗驗證與結果分析

4.1 數據來源及處理

實驗數據的提供方是中國科學院南海海洋研究所，選取我國南海17.5°N/110.5°E、17.8°N/110.7°E、18°N/111°E分別表示為A、B、C的三個點從2020年4月20日中午12時至2020年4月25日中午12時為期時長5 d的風速數據分別進行實驗，前4 d數據作為模型的訓練數據，最后一天數據作為測試數據。

4.2 SARIMA模型的構建和檢驗

以A點為例，首先對風速時間序列進行STL分解，結果見圖5。

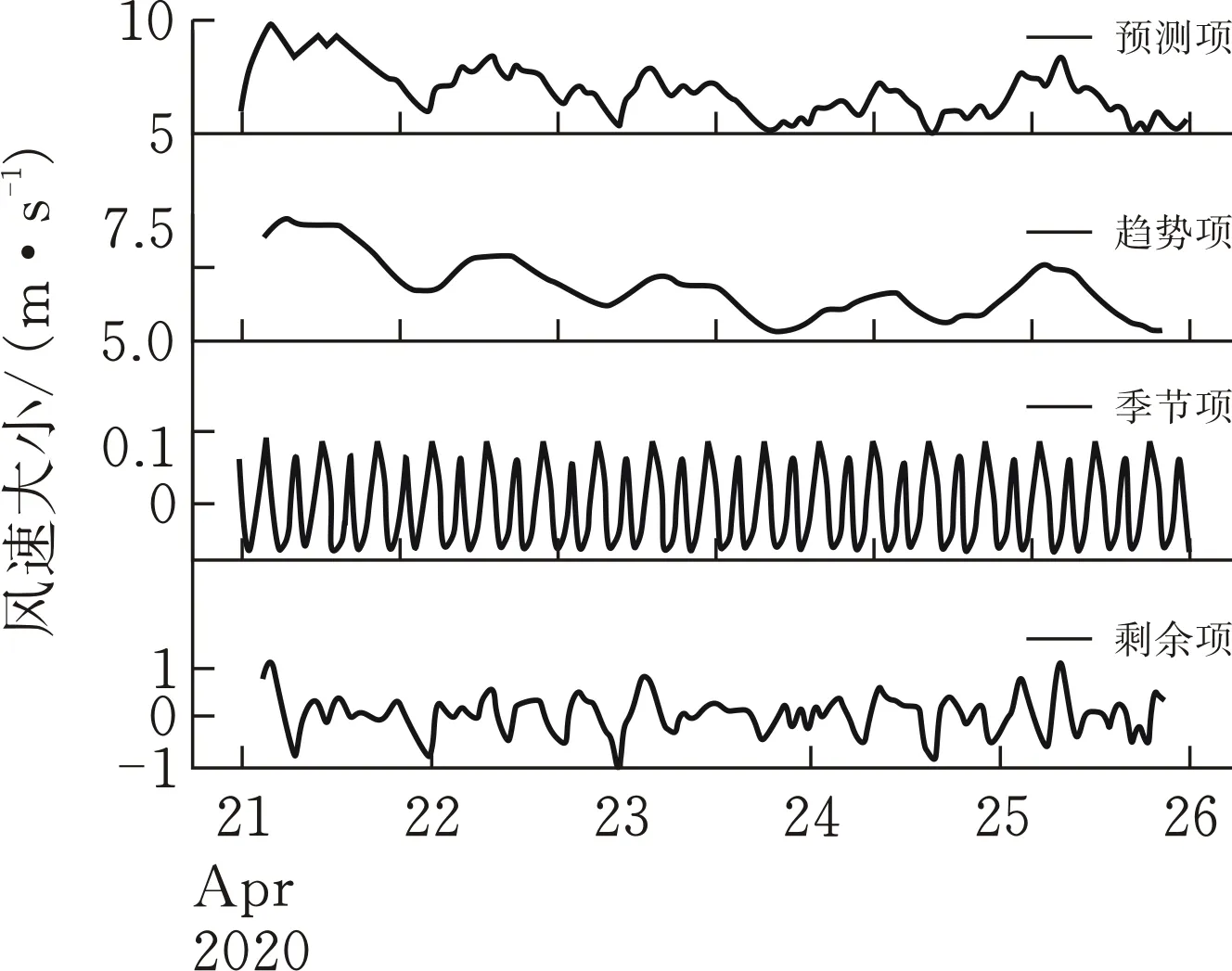
圖 5 風速時間序列分解示意圖

從圖5中可以看出觀測的風速序列整體在前4 d存在明顯的下降趨勢，最后一天稍微有所上升，每一天內都呈現出先上升后下降的趨勢。由于實測的數據是以小時為單位進行觀測得到，因此確定SARIMA(p，d，q)(P，D，Q)s模型中的季節性差分步長s的值為24。

模型的參數確定通過網格搜索的方式進行，參數搜索范圍確定為0～2，確定了模型的參數后，需要對模型進行檢驗，主要是進行模型的顯著性檢驗和參數的顯著性檢驗。模型參數及其顯著性檢驗信息見表1，檢驗方法采用Z值檢驗。結果表明該模型參數均顯著非零，模型參數均通過檢驗。

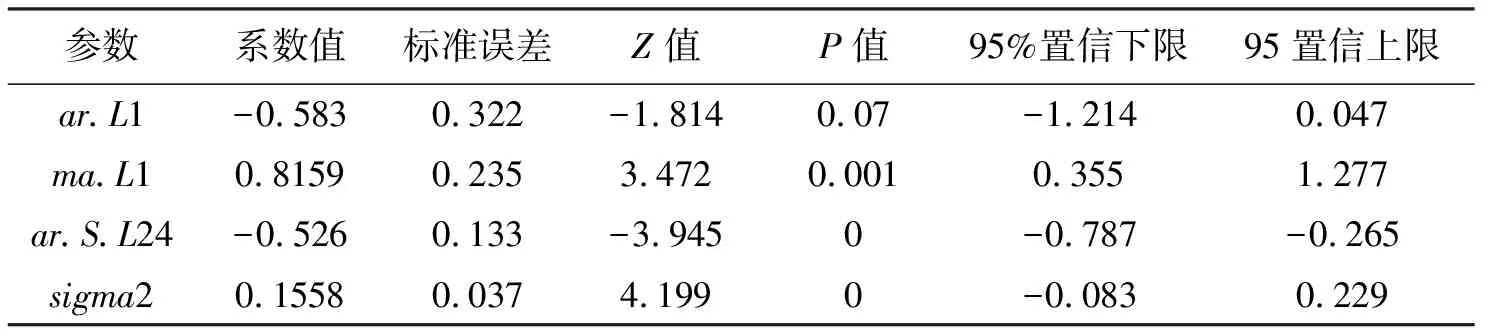
表1 模型參數與參數顯著性檢驗

采用相同的方式對B、C兩點的風速數據進行同樣的建模處理，最后使用得到的模型對觀測到的風速數據進行提前一天的預測，得到的風速實際預測值和風速觀測值對比結果見圖6。

(a)A點

觀察以上三個地點風速的觀測值和預測值的結果曲線，預測值曲線的整體波動趨勢與觀測值曲線的波動趨勢基本一致，但在風速波動較大時，預測精度還有待提升。

4.3 SARIMA-LSTM模型風速預測

在SARIMA-LSTM組合模型中，先使用風速的觀測值進行SARIMA模型建模，將模型得到的殘差作為LSTM模型的輸入。為了實現對模型殘差進行準確的預測，設計了圖7所示的殘差預測LSTM網絡結構。

圖 7 殘差LSTM網絡結構

設置LSTM網絡的輸入維度和輸出維度都是1維，隱藏層神經元節點的個數為120，損失函數設置為均方誤差函數(MSE)，優化器選擇Adam, 對模型進行訓練。網絡的輸出信息見圖8。加入LSTM網絡后，組合風速預測模型在A、B、C 三點的預測效果見圖9。

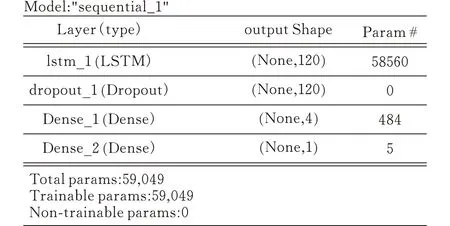
圖 8 LSTM網絡信息輸出

(a)A點

從實驗結果可以看出，在SARIMA模型的預測基礎之上增加長短時記憶網絡后的預測結果值與原始的風速值更為接近，預測曲線的變化趨勢與實際觀測風速曲線的變化趨勢也基本一致。

4.4 SARIMA-LSTM模型風速預測

為了驗證改進后組合模型在風速預測中的有效性，在相同的實驗條件下，分別使用SARIMA模型、BP網絡模型、LSTM網絡模型、LSTM-SARIMA組合模型和本文的STL-SARIMA-LSTM組合模型進行實驗對比。預測誤差選取3個不同地點平均絕對誤差MAE、均方根誤差RMSE和平均絕對百分比誤差MAPE的均值作為評價標準。定義見公式(3)～(5)。

(3)

(4)

(5)

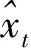
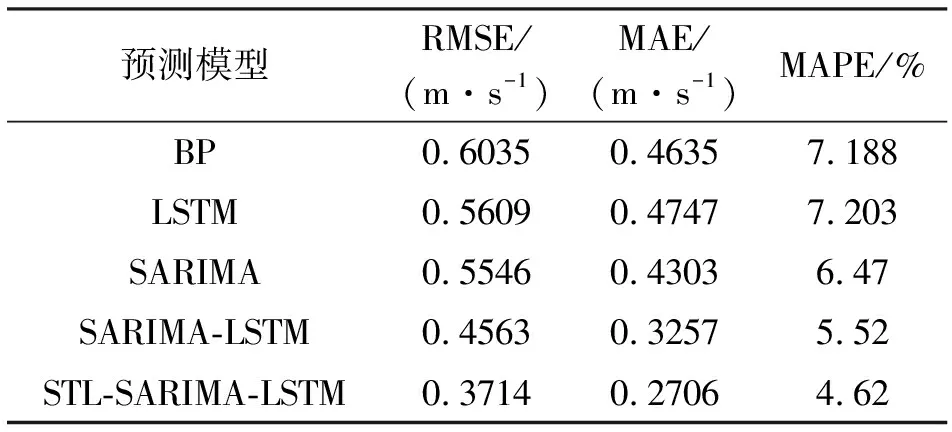
表2 預測結果對比

由表2可知: 單一預測模型中，SARIMA模型預測效果較好，LSTM神經網絡模型和BP神經網絡模型的預測精度相差不大。由于組合模型對海上風速數據特征的提取更加充分，預測精度高于單一預測模型。使用LSTM和SARIMA組合時預測誤差較小，而當在SARIMA模型季節性差分參數確定時，考慮結合STL后，再結合LSTM進行海上風速的預測時，預測風速曲線與實際風速曲線最為接近，預測精度最高。

5 結論

在STL分解海上風速序列后，SARIMA模型的季節性差分步長確定變得更為準確，從而使其預測精度得到了提升。從一系列的對比實驗中可以看出改進后的SARIMA與LSTM組合后對于海上風速預測的精度更高。加入STL后模型變得更為復雜，導致數據處理的時間變長且由于海上風速的不穩定性，在風速波動較大點預測精度還不夠好。后續研究應進一步優化模型并考慮諸如氣壓、溫度等額外因素對于海上風速大小的影響。