連續(xù)-非連續(xù)數(shù)值分析課程建設(shè)規(guī)劃

張一鳴 王雪雅 馮春 叢俊余

摘? 要：連續(xù)-非連續(xù)數(shù)值分析是一門擬建的土建類本科生/研究生課程，該課程理論與實踐性兼?zhèn)洌婕爸T多力學、數(shù)學相關(guān)基礎(chǔ)課程，包含課堂教學以及上機操作模塊。課程以土木建筑和巖土工程中的連續(xù)-非連續(xù)問題為研究對象，以數(shù)值計算方法為手段，以培養(yǎng)學生將課程中獲取的知識用于分析具體工程問題為目的。課程的建設(shè)不僅符合我國在中國智能建造2035背景下對于新一代土建類工科學生的培養(yǎng)目標，更契合我國目前在基礎(chǔ)設(shè)施防災(zāi)減災(zāi)、能源開采、節(jié)能減排方面的長期重大需求。

關(guān)鍵詞：土木工程;本科生/研究生課程;數(shù)值計算;防災(zāi)減災(zāi);能源開采

中圖分類號：G640 文獻標志碼：A? ? ? ? ? 文章編號：2096-000X（2022）04-0100-04

Abstract： Continuous and Discontinuous Numerical Analysis is a proposed undergraduate graduate course in civil engineering. The course has both theory and practice， involving many basic courses related to mechanics and mathematics， including classroom teaching and computer operation modules. The course takes the continuous discontinuous problems in civil architecture and geotechnical engineering as the research object， takes the numerical calculation method as the means， and aims to train students to use the knowledge obtained in the course to analyze specific engineering problems. The construction of the course is not only in line with China's training objectives for a new generation of civil engineering students under the background of China's intelligent construction 2035， but also in line with China's long-term major needs in infrastructure disaster prevention and reduction， energy mining， energy conservation and emission reduction.

Keywords： civil engineering; undergraduate and graduate courses; numerical calculation; disaster prevention and mitigation; energy exploitation

在土木水利能源開采等多種工程實踐中，連續(xù)-非連續(xù)過程是一類較為常見、較復雜且分析難度較大的工程問題，較為典型的包括：房屋結(jié)構(gòu)長期服役后的微裂縫與宏觀裂縫開展，大體積混凝土澆筑后的水化裂縫形成，頁巖氣開采過程中水力壓裂縫網(wǎng)絡(luò)形成等。在這些不同的工程中，非連續(xù)位移場的具體表現(xiàn)即裂縫扮演著不同的角色，在某些工程中裂縫會危害結(jié)構(gòu)局部甚至整體的正常使用性能和長期耐久性，應(yīng)研究如何預測、避免裂縫形成降低其危害;而在另一些石化能源采集相關(guān)的工程中，合適的裂縫網(wǎng)絡(luò)可以顯著提升油氣開采效率，應(yīng)分析如何通過有限資源促進、誘導裂縫形成從而降低成本，提高利潤。

從數(shù)學角度來看，非連續(xù)意味著場函數(shù)的跳躍，在對應(yīng)位置的場函數(shù)無法對空間求導，原有的偏微分控制方程已不適用于描述裂縫處的非連續(xù)場。同時，由于裂縫的動態(tài)擴展，不斷進行移動邊界重構(gòu)又會造成嚴重計算負擔和復雜拓撲重構(gòu)，數(shù)十年來很多頂尖學者持續(xù)地提出諸多針對性的新理論、新模型和新方法。因此，由于所關(guān)聯(lián)工程問題的重要性和問題背后數(shù)學機理與數(shù)值算法上的復雜性，連續(xù)-非連續(xù)問題至今仍然是數(shù)值計算領(lǐng)域的前沿課題之一。

我國在傳統(tǒng)土建類本科生及研究生的培養(yǎng)過程中，對于傳統(tǒng)的工科三大力學即理論力學、材料力學和結(jié)構(gòu)力學較為重視，很多高校更會在本科階段就輔以彈性力學、塑性力學等進階固體力學類課程，同時多數(shù)高校對于數(shù)值分析課程上機操作也有一定要求。這些既有課程為連續(xù)-非連續(xù)數(shù)值分析課程的開展創(chuàng)造了必要條件和基礎(chǔ)鋪墊，本課程的建立更符合遞進式的人才培養(yǎng)規(guī)律，可以加深對既有知識的認識，同時讓學生接觸前沿問題，能夠幫助學生深入領(lǐng)會數(shù)學、力學理論與工程實踐的緊密聯(lián)系，并通過上機操作解決具體工程問題，掌握分析方法、流程并撰寫較為嚴謹?shù)恼n題報告。

綜上所述，筆者在本文中提出了連續(xù)-非連續(xù)數(shù)值分析課程的建設(shè)規(guī)劃，梳理了課程所需要的背景知識，提出了主要授課內(nèi)容，授課內(nèi)容的邏輯路線，上機操作要點，小組任務(wù)計劃以及課畢后的考試要素等。本文的論述過程中緊盯課程授課目標，強調(diào)授課內(nèi)容邏輯，注重操作與實踐，希望本文能對連續(xù)-非連續(xù)數(shù)值分析課程建設(shè)和最終落地做出貢獻。

一、課程路徑

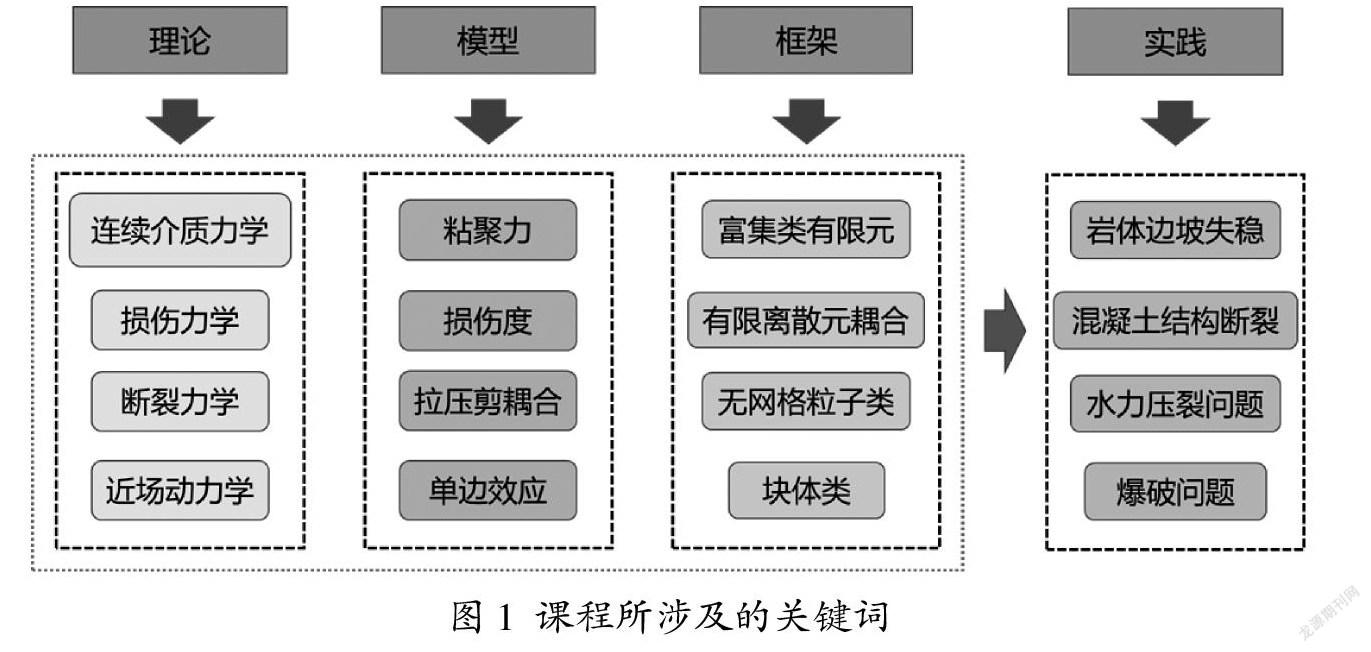
如前所述，工程上的連續(xù)-非連續(xù)過程往往指代連續(xù)體從初始的連續(xù)狀態(tài)逐漸進入非連續(xù)狀態(tài)的較為完整的演化過程，即裂縫的萌生、擴展，甚至后期的分叉交錯過程。而連續(xù)-非連續(xù)數(shù)值分析課程同樣應(yīng)依據(jù)該過程的時間發(fā)展順序展開，需要包含多個過程中所涉及的理論、模型以及計算框架。若以關(guān)鍵詞的形式給出本課程教授所涉及到的內(nèi)容，那么課程所涉及的多數(shù)關(guān)鍵詞，如圖1所示。

本課程涉及的理論中，連續(xù)介質(zhì)力學可由鋪墊課程如彈性力學和塑性力學逐步展開，再次提供控制方程后即可直接過渡到損傷力學相關(guān)知識，損傷力學的理論部分與損傷度模型可同步講授。接著加入討論環(huán)節(jié)，深化理解后可展開至斷裂力學，該部分內(nèi)容應(yīng)突出其與其他力學理論的差異，引入裂尖場的概念。近場動力學理論作為較新的理論，可由授課人選講。至此，理論部分授課告一段落。

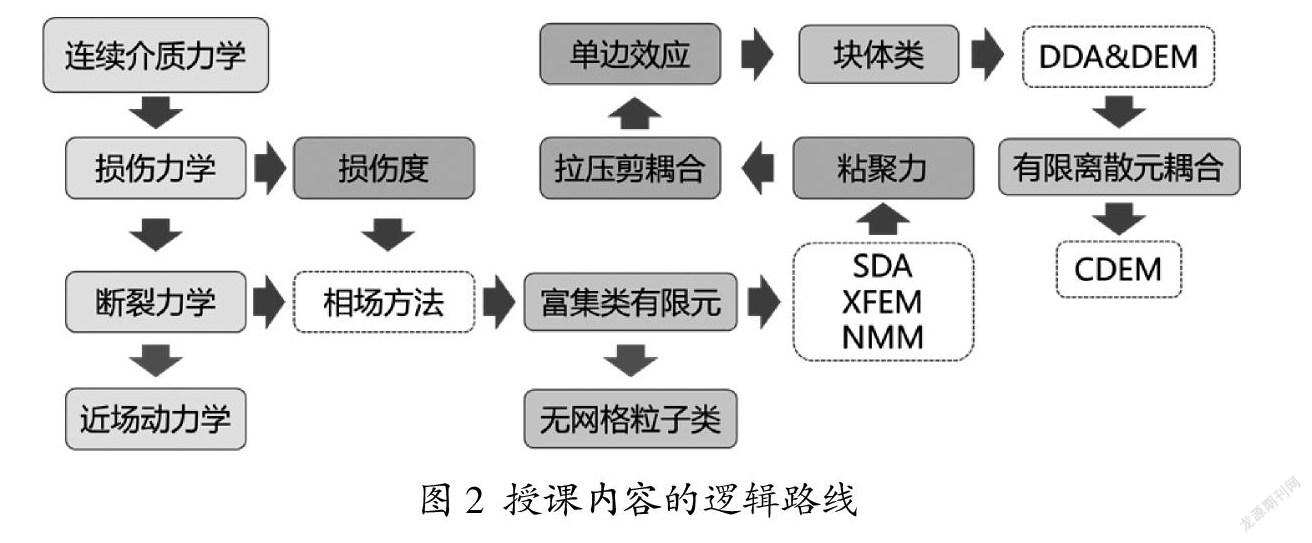
由于損傷力學與斷裂力學都鋪墊完成，下一步可展開講授，將相場方法[1]作為結(jié)合損傷力學與斷裂力學理論的方法實例，并進一步引出富集有限元即通過引入額外自由度來增強有限元框架的理念。當富集類有限元介紹完成后，可較為順暢地引入內(nèi)嵌不連續(xù)方法（SDA）[2]，擴展有限元（XFEM）[3]以及數(shù)值流形方法（NMM）[4]作為其他富集類方法實例，同時在講授這些方法的過程中逐漸引入粘聚力模型以及拉壓剪耦合模型相關(guān)內(nèi)容，無網(wǎng)格粒子類方法由于與近場動力學有一定關(guān)聯(lián)性，可作為選講內(nèi)容。接著過渡到與巖石破壞關(guān)聯(lián)緊密的單邊效應(yīng)并引出塊體類計算框架，以非連續(xù)分析方法（DDA）[5]和顯式離散元（DEM）[6]作為方法實例，最后引出有限離散元耦合方法，以基于廣義拉格朗日方程的連續(xù)非連續(xù)單元法（CDEM）[7]為實例。如圖2所示，標注了課程的整體講授路線。

本文所建議的授課流程依循理論層進，強化模型與框架，同步展開方法實例的脈絡(luò)。在展開實例后，結(jié)合上機操作，可讓學生掌握方法的使用，即使內(nèi)在運行機制尚未完全熟悉，仍然可為學生提供足夠檢索信息，讓他們根據(jù)路線圖返回尋找關(guān)鍵步驟。例如，當學生自覺對于相場方法缺少足夠認識，可前退至斷裂力學，損傷力學與損傷度，后進至富集類有限元搜尋相關(guān)概念知識并檢索相關(guān)文獻。另一方面，圖2的所有實例化方法，都可在“連續(xù)-非連續(xù)光譜”[8]上找到近似位置，如圖3所示。從該光譜的位置看，圖2的路線是從連續(xù)模型出發(fā)，逐漸過渡到離散模型，即從光譜的左側(cè)平滑過渡到右側(cè)的過程，也如前所述，符合結(jié)構(gòu)體的演化方向即時間發(fā)展順序。

二、具體授課內(nèi)容與比例

本課程授課內(nèi)容較多，并且與其他課程有較強關(guān)聯(lián)性，有必要對授課內(nèi)容與課時比例展開規(guī)劃。本課程如果為本科生課程，建議作為本科三年級下課程。若作為研究生課程，建議為碩士研究生課程，博士研究生由于專業(yè)背景差異較大，筆者認為不宜展開授課，可自學，建議總課時數(shù)不少于32課時。

課時分配建議：連續(xù)介質(zhì)力學與數(shù)值計算方法理論2課時，損傷力學+損傷度模型2課時，斷裂力學2課時，相場方法2課時;富集類有限元2課時;SDA，XFEM，NMM三類方法重點教授一類，討論2類，并討論粘聚力模型，共5課時，拉壓剪耦合與單邊效應(yīng)模型講授2課時，塊體類模型結(jié)合DDA以及DEM講授3課時，有限離散元耦合以及實例化的CDEM方法4課時。剩余8課時可抽取2課時選講近場動力學與粒子類方法，剩余課時作為上機課程。本課程的開展基于學生已學習過工科三大力學并且對于彈性力學、塑性力學課程有一定了解的基礎(chǔ)上，因此部分內(nèi)容授課安排較為緊湊，后續(xù)部分筆者將進一步細化具體授課內(nèi)容作為一般建議。

連續(xù)介質(zhì)力學加數(shù)值計算章節(jié)，強化彈性力學偏微分控制方程及其弱形式概念，包括常見邊界條件的類型、設(shè)置，介紹1至2種形函數(shù)后直接求解一個例題作為結(jié)束，建議求解一個二維的懸臂深梁或二維薄板拉伸算例，剖分為1至2個單元，直接以有限元形式手動求解，此算例即為基礎(chǔ)算例，在后續(xù)引入多種理論、方法、模型后不斷考慮不同條件與不同模型對該算例進行計算對比，不斷深化學生認知。

損傷力學與損傷度模型章節(jié)，強化不可逆損傷度的概念，介紹1至2種損傷度本構(gòu)和相關(guān)模型，輔以優(yōu)化求解算法，繼續(xù)以基礎(chǔ)算例為例，可結(jié)合彌散裂縫等較為傳統(tǒng)的計算模型，分析考慮損傷條件下的結(jié)構(gòu)位移-荷載響應(yīng)以及對應(yīng)的應(yīng)力-應(yīng)變狀態(tài)變化。

斷裂力學章節(jié)，引入裂尖狀態(tài)方程和應(yīng)力強度因子等概念，如課時允許可同步介紹J積分等概念，在基礎(chǔ)算例中引入一個裂尖，簡單分析其裂尖狀態(tài)、裂縫擴展方向、擴展條件，提供解析解方程加深學生對斷裂力學問題的理解。

相場方法章節(jié)，論述相場模型與傳統(tǒng)的彌散裂縫模型，梯度損傷模型的異同，引入特征寬度和尺度不敏感相場模型（Unified Phase Field Method或Phase Field-Cohesive Zone Model），算例部分，由于相場模型存在網(wǎng)格相關(guān)性，即網(wǎng)格尺寸必須小于特征長度，因此無法對基礎(chǔ)算例進行手動求解，需借用計算機輔助求解，通過在初始算例中加入缺陷，考慮多種網(wǎng)格與特征長度，觀察局部損傷區(qū)（相場云圖）的形成，此處的破壞僅考慮拉伸破壞。

富集類有限元與SDA、XFEM、NMM以及粘聚力模型章節(jié)可合并授課，其從相場模型出發(fā)，以引出富集策略、即引入額外自由度和對應(yīng)的控制方程來拓展原有的有限元計算框架，從而提升其適用范圍，基于不同方法對基礎(chǔ)算例進一步展開研究，并與相場的計算結(jié)果作對比，同步觀察上一章節(jié)的損傷區(qū)和本章節(jié)的離散裂縫發(fā)展過程，分析其異同。

拉壓剪耦合與塊體類計算框架可合并授課，由于拉壓剪耦合問題有較強工程背景，可關(guān)聯(lián)至巖土工程防災(zāi)減災(zāi)中涉及的連續(xù)-非連續(xù)問題，本章節(jié)授課建議結(jié)合上機操作，可以巖石邊坡穩(wěn)定問題為工程背景，突出該問題中所涉及的巖石復雜破壞機理，展示DDA和DEM計算方法在這類問題中的計算結(jié)果和計算效率，從而討論兩者的優(yōu)勢與適用范圍。

最后的授課內(nèi)容為有限離散元耦合分析框架，結(jié)合CDEM計算程序章節(jié)合并授課，結(jié)合上機操作，進一步分析上一章節(jié)所討論的巖石邊坡問題，獲得結(jié)果后與原始的DDA、DEM等計算結(jié)果作對比，討論其結(jié)果差異、性能、優(yōu)缺點等特征，明確其工程適用范圍。

選講內(nèi)容即近場動力學與粒子類方法章節(jié)，可直接提供二維條件下近場格式的積分控制方程，以顯示其與傳統(tǒng)連續(xù)介質(zhì)力學的差異，然后對基礎(chǔ)算例進行計算分析，考慮不同顆粒密度，觀察其損傷度演化過程，并與其他方法的計算結(jié)果和計算效率進行對比。

授課內(nèi)容完成后，對整個授課內(nèi)容進行梳理和總結(jié)，通過邏輯框圖、性能、適用范圍、結(jié)果特性對比表等多種形式提升學生的學習維度，提高他們對于連續(xù)-非連續(xù)問題的整體認識。

三、上機操作與考試考察

上機操作是本課程教學一大重點，通過分析具體算例使學生掌握部分數(shù)值計算軟件操作流程、結(jié)果分析和報告撰寫方法。目前，本課程所涉及的實例計算方法，大多數(shù)已有開源或商業(yè)軟件提供支持，例如相場模型有開源的Abaqus二次開發(fā)模塊，Abaqus自帶幻影點法（XFEM變種）計算模型，LS-Dyna支持近場動力學顯式積分計算，SDA、XFEM與NMM有開源的C以及MATLAB算法庫，DDA和DEM有成熟的開源算法庫，包括高性能矩陣離散元MatDEM等強化支持，更有基于廣義拉格朗日方法的全國產(chǎn)有限離散元耦合GDEM，環(huán)境平臺Genvi等計算套件。這些都為上機操作以及學生自主二次開發(fā)提供了便利。

上機操作總課時中，筆者建議相場可占20%，SDA、XFEM和NMM可占25%，DDA和DEM可占20%，剩余35%上機課時可留給CDEM和選學內(nèi)容，建議可進行多個案例的分析操作，這幾個案例中巖體邊坡失穩(wěn)分析可通過CDEM、DDA和DEM進行分析，對比結(jié)果并撰寫報告。第二個案例混凝土結(jié)構(gòu)斷裂可通過相場以及SDA & XFEM & NMM計算對比，第三個案例水力壓裂建議通過CDEM方法和XFEM進行分析對比，測試不同邊界條件對壓裂區(qū)的影響。第四個案例爆破問題建議通過CDEM、DEM和近場動力學方法進行分析。

考慮到課程人數(shù)與課時限制，筆者建議以小組式案例分析模式來促進教學，即由學生組成4至5人研究小組，分組后表決選舉組長，挑選具體案例，并對組員工作任務(wù)進行分配，尤其是涉及方法對比時，由組員根據(jù)自身興趣進行選擇，完成計算后展開集中討論，并由組員相互輔導，從而保證每個組員都可以至少掌握一種方法，并了解其他方法。在結(jié)果分析階段，應(yīng)由組長收集組員的問題，組內(nèi)討論后由授課老師答疑，若有必要可開展班級討論。然后以小組為單位完成書面工程報告，由組長進行答辯匯報，結(jié)合必要的現(xiàn)場演示，完善上機操作過程。

本課程考試考察可采用多種形式結(jié)合的方式，例如小組工程分析報告結(jié)合單人筆試測驗，測驗中重點考察相關(guān)概念，不同方法的區(qū)分，適用范圍等知識，筆試測驗以選擇題、填空題和判斷題為主。不宜過于側(cè)重具體計算，但可適當考察上機操作過程中的計算流程，分析步驟等內(nèi)容，例如由學生補充流程圖中的關(guān)鍵環(huán)節(jié)等。

四、結(jié)論與展望

在本文中，筆者提出了連續(xù)-非連續(xù)分析課程建設(shè)目標、建設(shè)要點、課程內(nèi)容以及具體授課安排，可供相關(guān)領(lǐng)域的專業(yè)人員參考。本課程除了理論性強，涉及的實例方法也較多，由于相關(guān)領(lǐng)域的進展較快，為了更好地反映學科發(fā)展，建議每年都對本文中所涉及的實例方法進行更新，每2年對實例化方法所涉及的上機操作軟件進行更新。另一方面，交叉學科進一步融合成為目前工程前沿發(fā)展一大特色，以本課程為例，目前已有學者提出采用機器學習方法預測、計算機圖形學加速模擬、全尺寸模型大規(guī)模混合云計算等各類較新穎的計算方法來分析研究連續(xù)-非連續(xù)問題，并取得了一定的成果。這些進展對于課程的未來建設(shè)和改進提出了新的要求和思路，相關(guān)內(nèi)容的擴充將助力培養(yǎng)中國智造2035背景下的優(yōu)秀土建類人才。

參考文獻：

[1]J.-Y. Wu. A uni？覱ed phase-？覱eld theory for the mechanics of damage and quasi-brittle failure[J].Journal of the Mechanics and Physics of Solids， 2017，103：72-99.

[2]Y. Zhang， R. Lackner， M. Zeiml， et al. Strong discontinuity embedded ap-proach with standard SOS formulation： Element formulation， energy-based crack-tracking strategy， and validations[J].Computer Methods in Applied Mechanics and En-gineering， 2015，287：335-366.

[3]A. Combescure， A. Gravouil， D. Gr'egoire， et al. X-FEM a good candidate for energy conservation in simulation of brittle dynamic crack propagation[J].Computer Methods in Applied Mechanics and Engineering，2008，197：309-318.

[4]H. Fan， H. Zheng， S. He. S-R decomposition based numerical manifold method[J].Computer Methods in Applied Mechanics and Engineering， 2016，304：452-478.

[5]H. Zheng， P. Zhang，X. Du.Dual form of discontinuous deformation analysis[J].Computer Methods in Applied Mechanics and Engineering， 2016，305：196-216.

[6]C. Liu， ed.， Matrix Discrete Element Analysis of Geological and Geotechnical Engi-neering[J].Springer Singapore， 2021.

[7]C. Feng， S. Li， X. Liu， et al.A semi-spring and semi-edge combined contact model in cdem and its application to analysis of jiweishan landslide[J]. Journal of Rock Mechanics and Geotechnical Engineering， 2014，6（1）：26-35.

[8]Y. Zhang， Z. Gao， Y. Li， et al. On the crack opening and energy dissipation in a continuum based disconnected crack model[J].Finite Elements in Analysis and Design， 2020：170.