“勾股定理小結與思考”教學設計與反思

■陳冠軍

一、教學目標

熟識勾股定理及勾股定理的逆定理，能將實際問題建模轉化為數學問題，能靈活應用所學知識解決問題，同時滲透方程、轉化等數學思想，進一步發展“有條理地思考”和“有條理地表達”的能力，體會數學的應用價值。

二、教學重點

將知識點形成鏈，建立相互關聯的知識結構，掌握科學的學習方法。

三、教學難點

構造直角三角形并借助方程、分類等思想解決數學問題。

四、教學流程

1.情境導學，明晰內容。

師：勾股定理是人類的寶貴財富，勾股定理及其逆定理在現實生活中有廣泛的應用。本章我們一起研究過它——直角三角形（板書），今天我們將一起復習這一章。本章我們學習了哪些數學知識和數學方法？大家能取其要點，構建框圖嗎？

生1展示構建的知識框圖，如圖1。學生之間相互點評。

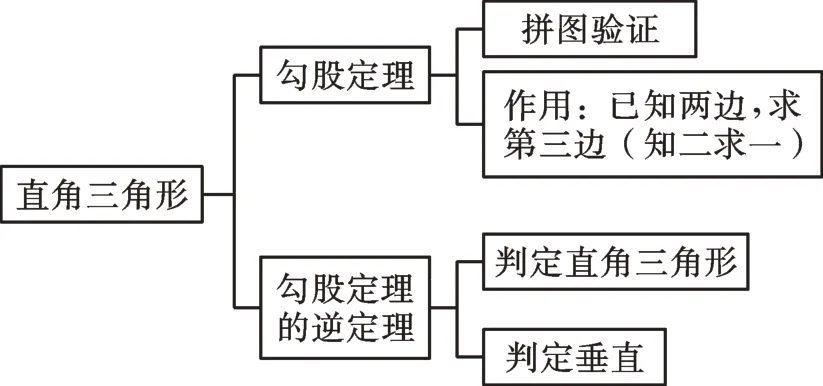
圖1

2.多元評學，以情勵學。

師：本章我們學習了勾股定理、勾股定理的多種證法，用不同的方法計算同一個圖形的面積，還有勾股定理的逆定理以及勾股定理、勾股定理逆定理在現實生活中的應用等。接下來，我們來看幾個問題。

師：例題1，（1）如圖2，已知在△ABC中，∠B=90°，一條直角邊為a，斜邊為b，則另一條直角邊c滿足c2=。

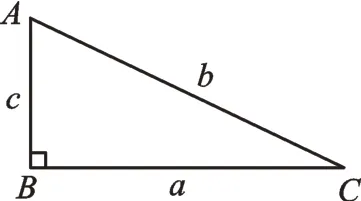
圖2

生2：根據勾股定理，可得c2=b2-a2。

師：（2）如圖3，在Rt△ABC中，∠C=90°。

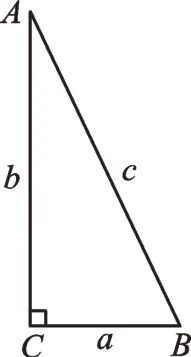
圖3

師：請同學們分小組合作，完成以上問題。

小組推薦代表1：已知直角三角形的兩條直角邊，求斜邊。根據勾股定理，得c2=a2+b2=32+42=9+16=25，解得c=5或-5。∵c＞0，∴c=5。

小組推薦代表2：已知直角三角形的一條直角邊，一條斜邊，求另一條直角邊。根據勾股定理，得c2=a2+b2，102=62+b2，b2=64，解得b=8或-8?！遙＞0，∴b=8。

小組推薦代表3：可設a=3k，b=4k（k＞0）。根據勾股定理，得c2=a2+b2，求得c=5k（負值舍去），則

師：通過例題1，我們初步復習了勾股定理、勾股定理的逆定理。接下來，我們繼續看例題2。

師：例題2，（1）如圖4，以Rt△ABC的三邊a、b、c為邊，向外作正方形，正方形面積分別為S1、S2、S3，則S1、S2、S3有什么關系？

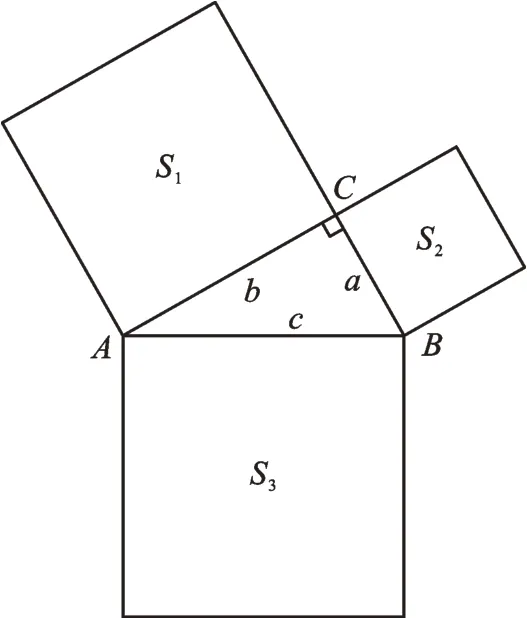
圖4

生3：∵△ABC是直角三角形，∴AC2+BC2=AB2，又∵S1=AC2，S2=BC2，S3=AB2，∴S1+S2=S3。

師：（2）以Rt△ABC的三邊a、b、c為邊，向外作等腰直角三角形（如圖5），等腰直角三角形面積分別為S1、S2、S3，或者以三邊a、b、c為直徑，向外作半圓（如圖6），半圓的面積分別為S1、S2、S3，則S1、S2、S3有什么關系？

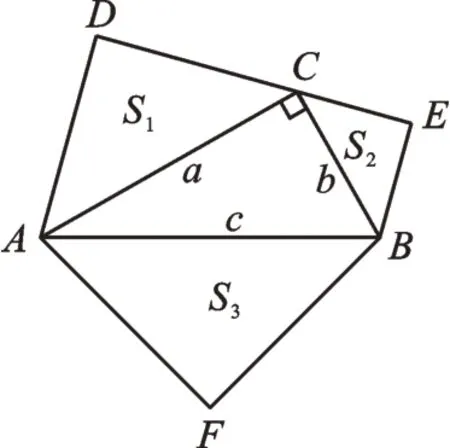
圖5

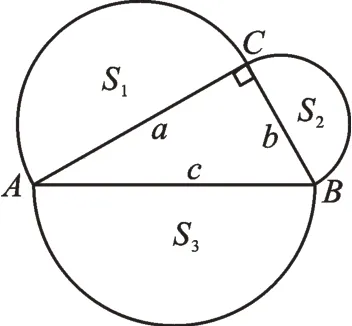
圖6

教師組織學生進行生生合作，共同探究得出S1+S2=S3。

師：（3）以△ABC的三邊a、b、c為邊，向外作正方形（如圖4），或等腰直角三角形（如圖5），或以三邊為直徑的半圓（如圖6）。若S1+S2=S3成立，則△ABC是直角三角形嗎？

師：這實際上是將之前問題的條件和結論互換，這樣變式，結論成立嗎？

教師“導”，學生“學”，學生在“對學”和“群學”中共同研究問題，解決問題，得出△ABC始終是直角三角形。

師：例題3，（1）已知，如圖7，將長方形的一邊BC沿CE折疊，使得點B落在AD邊的點F處，已知AB=8，BC=10，求BE的長。

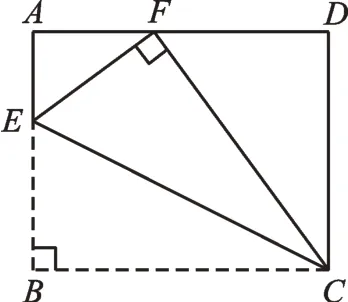
圖7

師：由AB=8，BC=10，易知哪些線段的長？請在圖中標出來。

師：在Rt△DFC中，你可以求出DF的長嗎？請在圖中標出來。

師：由DF的長，你還可以求出哪條線段的長？請在圖中標出來。

師：設BE=x，你可以用含有x的式子表示出哪些線段長？請在圖中標出來。

師：你在哪個直角三角形中，可以應用勾股定理建立方程？你建立的方程是

通過以上對比分析，利用閱讀的外圍去理解淺閱讀，都失之偏頗。筆者認為，淺閱讀的淺應該更著重于閱讀本身，在閱讀的過程中，都是有淺入深的一個漸進過程。參與時間短、輕思考，即為淺閱讀，參與時間多、重思考，即為深閱讀。無論你讀的是什么書，目的怎樣，讀者是誰，無一不需要經過這個過程。那么，在由淺入深的這個過程中，首先都要進入淺閱讀，而在淺閱讀之后，經過主體自身的判斷，是否需要進入深閱讀。

生4：在Rt△DCF中，∵FC=BC=10，CD=8，在Rt△AEF中，∵∠A=90°，AE=8-x，∴42+（8-x）2=x2。

師：（2）如圖8，折疊長方形紙片，先折出對角線BD這條折痕，再折疊，使點A落在BD上的E處，折痕為DG，若AB=4，BC=3，求AG的長。

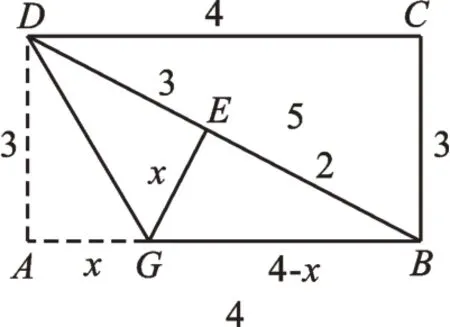
圖8

生5在黑板上板演：設AG的長為xcm，則x2+22=（4-x）2，解得解答過程略）。

師：還能用其他方法求AG的長嗎？

師：剛才我們以翻折問題為載體，利用方程思想，用“勾股定理”和“面積法”求出了AG的長。在生活中，我們也會遇到“最短路線問題”，下面我們一起來看例題4。

3.以練促學，當堂反饋。

師：例題4，如圖9，一條河同一側有兩個村莊A、B。A、B到河岸的最短距離分別為AC=1km，BD=2km。已知CD=4km，現欲在河岸上建一個水泵站向A、B兩村送水。水泵站建在河岸上何處時，從水泵站到A、B兩村鋪設的水管總長度最短？請求出最短距離。

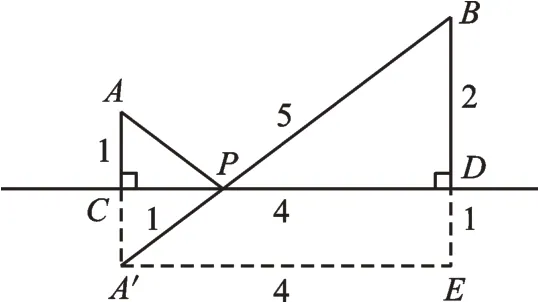
圖9

生7：作點A關于河流所在直線的對稱點A′，連接A′B，交河流所在直線于點P，點P即為所求，BE=3，A′E=4，∴A′B=5。

師：這個最短路線問題，需從無到有去構建“直角三角形”，再利用勾股定理解決問題。

師：例題5，圖10是一個三級臺階，它的每一級的長、寬和高分別為20dm、3dm、2dm，A和B是這個臺階兩個相對的端點。有一只螞蟻在A點，想到B點去吃可口的食物，則螞蟻沿著臺階面爬到B點的最短路程是多少？

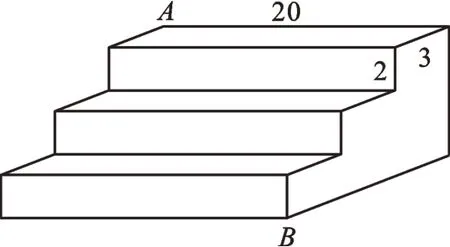
圖10

生8：可設螞蟻沿臺階面爬行到B點的最短路程為xdm，如圖11，由勾股定理，得x2=202+［（2+3）×3］2=252，解得x=25。

圖11

師：這個最短路線問題滲透了分類思想。借助于分類，我們可將復雜的問題簡單化。

4.回顧反思，學程總結。

師：通過本節課的學習，請大家談一談收獲。

學生各抒己見。

五、教學反思

張衛明名師工作室提倡“學生的實踐研究應該指向高階思維”，主張“在課堂教學中，應將低階思維和高階思維活動共同構成一個多樣化的、由低到高的層次式的課堂核心活動群，這樣才能實現在發展學生低階思維的同時，推動其高階思維的發展，進而實現課堂教學的有效性”，并提煉出“學程導航”的教學范式。

在設計本節課時，筆者從發展低階思維的“勾股定理的直接應用”入手，層層遞進到發展高階思維的“勾股定理在較復雜問題背景下的應用”，由低到高，體現了思維的發展?！皩W程導航”教學范式需要教師的“導”和學生的“學”共同作用來實現。充分而不過分的導尤為重要，能使學生自主地開展建構活動，構建一章的知識框圖，歸納重難點、易錯點。本節課中，筆者通過“教”“學”“用”教學環節，配以“獨學、對學和群學”等學習方式，讓學生獨立完成數學問題，在對學和群學中共同研究問題，解決問題，進而形成高階思維。如探究“最短路線問題”，筆者通過創設情境、提供任務的方式，保證了探究的充分和有效，同時，學生也完成了自我建構和共同建構，在課堂學習中優先指向高階思維目標的達成。筆者教方法，學生學方法，之后用方法遷移。所以，在教學過程中，教師應將學習知識的過程還給學生，通過對知識的深度等級劃分，找到“不可教”的地方，然后把“不可教”之處讓渡給學生。