基于PR控制器與不對稱SVPWM的永磁電機電流諧波抑制策略

雷 靂，羅 響，朱 莉

(上海交通大學 電氣工程系，上海 200240)

0 引 言

永磁同步電機(以下簡稱PMSM)具有結構簡單、體積小、質量輕、功率密度高等優點，近年來在國防航天、工農業生產及日常生活等領域中得到了廣泛應用。在常用的PMSM磁場定向控制系統中，受系統非線性因素影響，PMSM的電樞電流中含有一定諧波成分。這將增加電機損耗，并產生轉矩脈動與發熱等問題，降低控制系統的工作性能[1]。

引起PMSM諧波電流的因素有兩個：1)電機本體的非線性因素，如磁飽和效應、轉子磁極結構、繞組分布、齒槽效應等，均會引起電機氣隙磁場畸變，從而產生諧波電流；2)逆變器的非線性因素，包括開關器件的管壓降、死區特性等[2-3]。

從引起PMSM諧波電流的因素入手，國內外學者針對如何抑制諧波電流做了大量研究。考慮電機本體部分，改善電機氣隙磁場正弦度可有效削弱基波磁場外的諧波磁場分量，進而降低諧波電流[4-5]。然而，對電機氣隙磁場的優化往往提升了電機設計的復雜度和制造難度，難以推廣。

另一種思路從電機的控制策略出發，提取電機運行時的諧波電流，并設計補償器對諧波電流進行抑制。針對特定頻率諧波的抑制主要有兩種方法，一是重復控制，另一個是比例諧振(以下簡稱PR)控制[6]。

重復控制器在理論上對給定頻率的整數倍頻率信號均有無窮大幅頻響應，可應用于PMSM控制系統中消除電流諧波和轉矩脈動[7-8]。但重復控制器要求一定的存儲空間，算法較為復雜，且工況變化時對不同基頻需要重新設計控制器。

PR控制基于內模原理，具有正弦信號的內模模型。與重復控制器類似，理想PR控制器在諧振頻率點處有無窮大增益。與之不同的是，PR控制器的諧振頻率可自由設定，具有更高的設計自由度。且PR控制器結構簡單，易于整定參數，被廣泛應用于并網逆變器和PMSM的諧波抑制中[9-10]。但在實際應用中，受控制系統帶寬限制，針對高頻諧波設計的PR控制器的控制信號會被削弱，使得PR控制器對高頻諧波的抑制效果不佳。

針對PR控制器對高次諧波電流抑制效果減弱的問題，本文改進了PMSM控制系統中的空間矢量脈沖調制(以下簡稱SVPWM)算法，將其改造為輸出脈沖不再關于載波波形對稱的不對稱空間矢量脈沖調制(以下簡稱ASVPWM)算法，縮短了逆變環節的延遲時間，提升了電流環帶寬，顯著改善了PR控制器對高頻諧波的抑制效果。此外，ASVPWM算法相較于SVPWM具有部分自然采樣法的性質，可在維持開關器件開關頻率的前提下降低諧波含量。該算法與PR控制器聯合作用后，可對PMSM的17、19次高次諧波電流達到良好的抑制效果。仿真和實驗驗證了本文提出的諧波抑制策略的有效性。

1 PR控制器

1.1 永磁電機諧波分析

PMSM運行過程中，受電機本體和控制系統中的非線性因素影響，其定子電流中諧波成分較為豐富。文獻[11]分析得到了逆變器死區效應造成的諧波主要為基頻的3、5、7次等奇數次諧波。文獻[12]綜合考慮了電機本體設計非理想、齒槽效應和逆變器非線性特性產生的諧波，推導了電機諧波模型，得出電機穩態運行時電樞電流主要含有6k±1 (k=1,2,3，…)次諧波。假設電機星形連接，即可忽略3的倍數次諧波，那么在諧波抑制時只需考慮6k±1次諧波。

經坐標變換后，三相電流中的6k±1次諧波在d,q坐標系中表現為6k次諧波分量，即:

(1)

式中：Id0,Iq0為d,q軸電流直流分量；Id,6k,Iq,6k為d,q軸電流的6k次諧波分量；ω為基波角頻率；θd,6k,θq,6k為6k次諧波電流的初始相角。

經以上分析，在dq坐標系下抑制6k次諧波，即可抑制三相坐標系下的6k±1次電流諧波。

1.2 PR控制器原理

內模原理指出，一個能良好抵消外部擾動或跟蹤給定指令信號的反饋控制系統，其反饋回路中必須包含一個與擾動或指令信號相同類型的動力學模型[13]。PI控制器能良好跟蹤d,q軸的直流指令，但對前文分析的6k次諧波電流難以達到良好的抑制作用，為此，需引入PR控制器。

理想PR控制器含有正弦信號的內模，其傳遞函數：

(2)

式中：KP,KR分別為比例和諧振環節增益；ω0是諧振角頻率。PR控制器在諧振頻率處有無窮大幅頻增益。

在實際應用中，諧振頻率易因采樣誤差或轉速波動發生偏移，因此常用具有一定帶寬的準PR控制器，以提升魯棒性。其傳遞函數：

(3)

引入諧振帶寬ωb后可拓寬準PR控制器的諧振范圍，使其對諧振頻率附近一定范圍內的頻率信號均有正增益，可削弱因諧振頻率波動造成的系統控制性能下降。

1.3 PR控制器參數整定

為抑制電流諧波，諧振控制器通常與控制系統中電流環上的PI控制器并聯以組成PIR控制器，如圖 1所示(以d軸為例)。

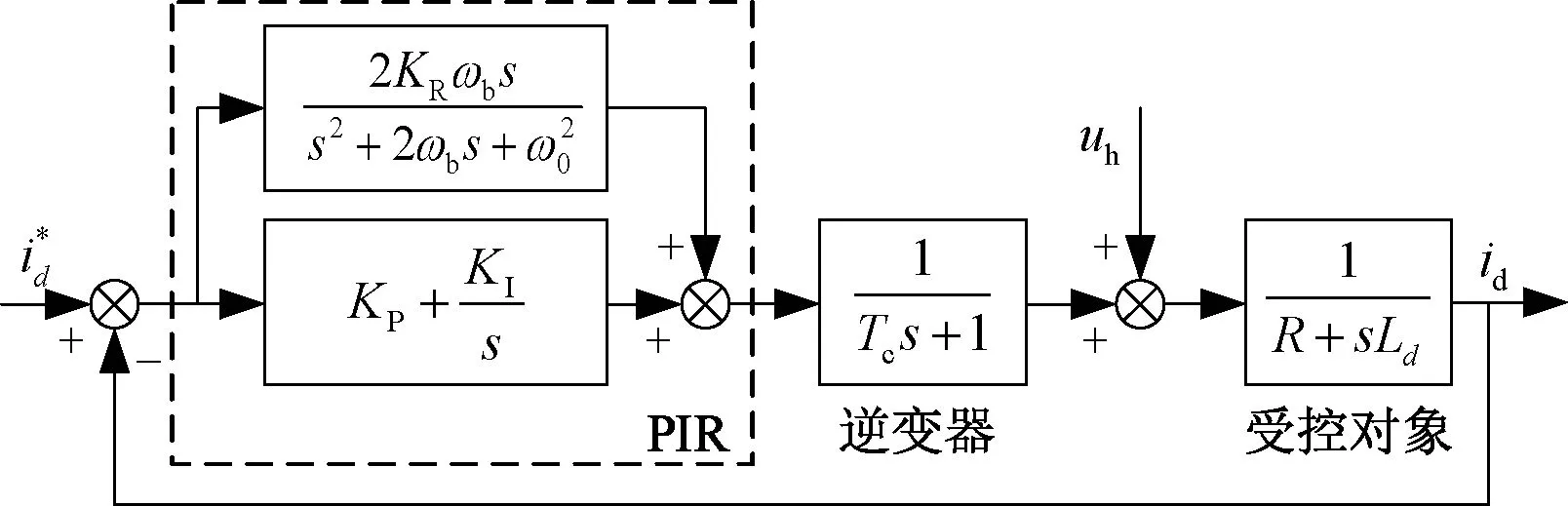
圖1 有諧振控制器的d軸電流環控制框圖

圖 1中，Tc為逆變器的延遲時間常數，uh為導致諧波電流的擾動電壓。在數字控制系統中，逆變器輸出的電壓脈寬需要由控制器采樣相電流值后計算得到，考慮到ADC采樣的轉換時延與電壓矢量的作用時延，逆變環節的延時通常是開關周期的1.5倍左右，即Tc=1.5TPWM。

在整定諧振環節參數前，需先整定PI控制器的參數。暫時忽略諧振環節，電流環的開環傳遞函數：

(4)

(5)

式(5)與典型I型系統的開環傳遞函數形式相同。按照最佳整定準則，取：

(6)

即可得到PI控制器的參數整定值：

(7)

此時電流環對擾動電壓uh的阻抗：

(8)

式中：ωh為uh的角頻率。而在引入諧振環節后，回路阻抗將變為：

ZPIR=R+sLd+

(9)

為抑制對應的頻率諧波，諧振環節的諧振頻率ω0應與ωh相等。諧振帶寬ωb可根據電機轉速脈動的大小在1～10 rad/s之間選取。在s=jωh時，式(9)可簡化：

(10)

對比式(8)與式(10)可以發現，在引入諧振環節后，電流環在諧波頻率處的阻抗增加了，且KR越大，回路阻抗越大。而諧振控制器又具有篩選特性，電流環對其他頻率信號的回路阻抗不會顯著增加，因此引入諧振環節后可以在不影響正常控制的前提下抑制對應頻率的諧波分量。KR的取值需綜合系統的穩定裕度考量，可在不威脅系統穩定性的前提下盡量取大。若系統內存在不同頻率的諧波，需要同時抑制，可在PI控制器上并聯多個諧振頻率不同的諧振環節，之后逐一確定各個諧振環節的KR取值。

1.4 電流環帶寬分析

經上文分析，引入諧振控制器后，電流環在諧振頻率處的回路阻抗增加，可有效抑制對應頻率的電流諧波。然而電流環實質上是一個低通系統，當存在頻率超過電流環截止頻率的高頻電流諧波時，對應設置的諧振控制器的控制信號會被衰減，無法有效地抑制諧波。為實現對高頻諧波的有效抑制，需要考察影響電流環帶寬的因素。

不考慮諧振環節，d軸電流環的開環幅頻響應：

(11)

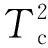
(12)

電流環的開環截止頻率ωc滿足：

(13)

可解得：

(14)

(15)

由式(15)可知，ωc與電機參數Ld、R呈正相關，與Tc呈負相關。在電機參數不能改變的前提下，本文提出不對稱的空間矢量脈沖調制算法，通過縮短Tc的方式提升系統帶寬，進而提高諧振控制器對高頻諧波的抑制效果。

2 ASVPWM

2.1 ASVPWM原理

目前，SVPWM算法被廣泛用作大功率傳動系統的驅動算法，其相比僅考慮生成正弦波電壓的SPWM算法提升了電壓利用率和控制性能。盡管SVPWM與SPWM算法的出發點不同，但經數學分析可以發現，SVPWM實際上是SPWM的一種改進，可由對SPWM調制波注入零序分量獲得，且本質上是一種規則采樣PWM[14]。

作為規則采樣PWM，SVPWM的采樣時刻通常在載波的波峰(或波谷)處，以決定下一個載波周期的輸出電壓脈沖寬度，且輸出脈沖關于載波對稱。ASVPWM在此基礎上改進而來，在載波到達正負峰值時均進行采樣，每個采樣值僅計算半個載波周期內的脈沖寬度。

圖 2展示了ASVPWM的時序圖。對于載波頻率為f的ASVPWM算法，其在載波的波峰與波谷處均進行ADC采樣，并立即計算出當前半周期內的PWM脈沖起始/終止時刻，對應開關管的導通/關斷時刻。如此，ASVPWM算法可與載波頻率為2f的SVPWM算法等效，并且在ASVPWM中的開關頻率并未增加，意味著其可以以低開關頻率實現與高開關頻率等效的PWM波。此外，ASVPWM輸出的每個電壓矢量的作用時間(即從其被采樣計算得出到其作用完畢的時間)不超過半個PWM周期，使得Tc=0.5TPWM。因此，ASVPWM算法的應用可以使得Tc縮短，達到提升系統的帶寬目的。

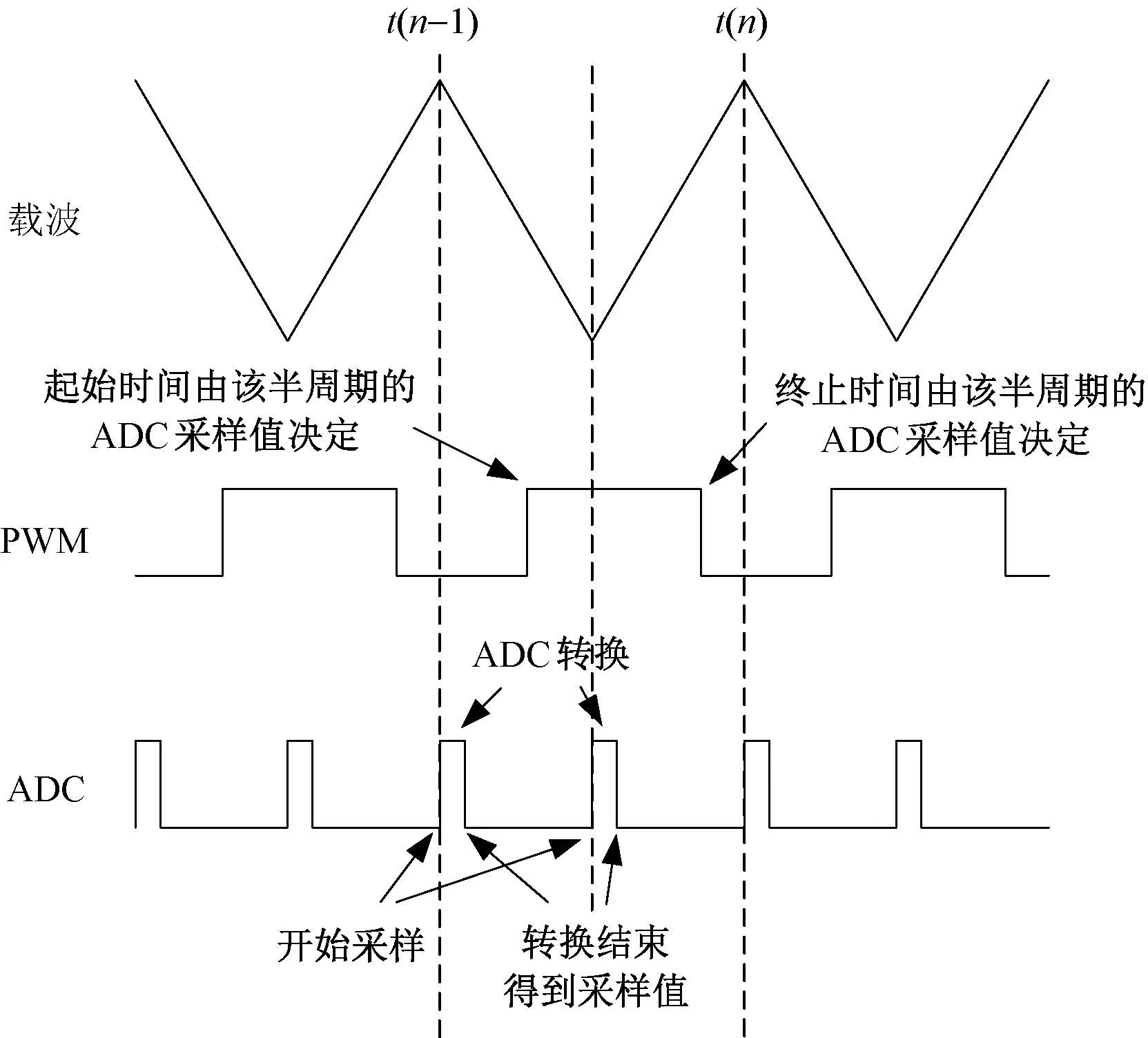
圖2 ASVPWM與ADC時序圖

2.2 ASVPWM的諧波特性

SVPWM與ASVPWM的目標都是通過基本電壓矢量的組合產生等效的參考電壓矢量，可以理解為在每個采樣周期內對三相參考電壓調制波采樣，而ASVPWM的采樣率比SVPWM高一倍。穩態下，三相參考電壓調制波應是與電機基波頻率相同的對稱三相正弦波。首先考慮SVPWM的諧波特性，以A相為例，設載波為uc(t)，周期為Tc；A相參考電壓調制波為urA(t)，周期為Tr，與基波周期相同。定義載波比M：

(16)

假定M為整數，則在一個周期內SVPWM算法應輸出M個脈沖。以t=0作為調制波采樣的起始時刻，設第i(i≤M)個載波周期[(i-1)Tc,iTc]內，A相上橋臂開關管的導通時刻、關斷時刻、導通時長分別為TAon(i)、TAoff(i)、TAP(i)。SVPWM是對稱規則采樣，TAon(i)、TAoff(i)、TAP(i)滿足：

(17)

設A相上橋臂開關管的狀態函數為SA(t)，則：

(18)

因urA(t)經過一個周期后，對應的電壓矢量在復平面上轉過一圈，開關狀態也經歷一個周期，故SA(t)是周期為Tr的周期函數，可以將其表示為復指數形式的傅里葉級數：

(19)

系數cAn滿足：

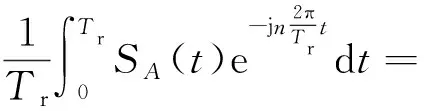
(20)

式中[15]：

(21)

(22)

設SVPWM輸出線電壓為uAB(t)，同樣將其表示為傅里葉級數：

(23)

同時:

uAB(t)=uA(t)-uB(t)=

Udc[SA(t)-SB(t)]=

(24)

可得：

cABn=Udc(XAn-XBn)·Wn

(25)

定性分析SVPWM線電壓中調制波的低次諧波含量。設n?M，有：

(26)

(27)

則：

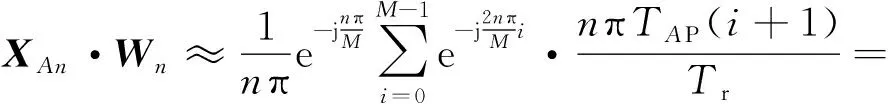
(28)

同理可得:

(29)

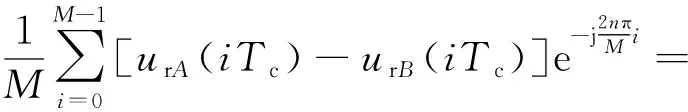
(30)

式(30)表明，SVPWM輸出的線電壓uAB(t)的調制波n次諧波系數cABn恰好與對urAB(t)做M點離散傅里葉變換的系數相同。同時，在上述推導過程中，系數cAn、cBn僅與各載波周期中對應的TP(i)有關，與Ton(i)、Toff(i)均無關，可以認為ASVPWM的脈沖不對稱性不改變ASVPWM輸出電壓的諧波特性，其輸出電壓的諧波特性與載波周期為Tc/2的SVPWM算法相同，輸出線電壓的諧波系數：

(31)

因此，ASVPWM輸出線電壓的調制波n次諧波系數c′ABn與對urAB(t)做2M點離散傅里葉變換的系數相同。在穩態下，urAB(t)應是一正弦波，同等開關頻率下，ASVPWM對調制波的采樣頻率是SVPWM的2倍，其輸出的線電壓調制波更接近原始正弦波，諧波特性優于同開關頻率下的SVPWM算法。

3 仿真及分析

3.1 單PR控制器

首先通過仿真驗證PR控制器對電流諧波的抑制效果。仿真用電機參數如表 1所示。

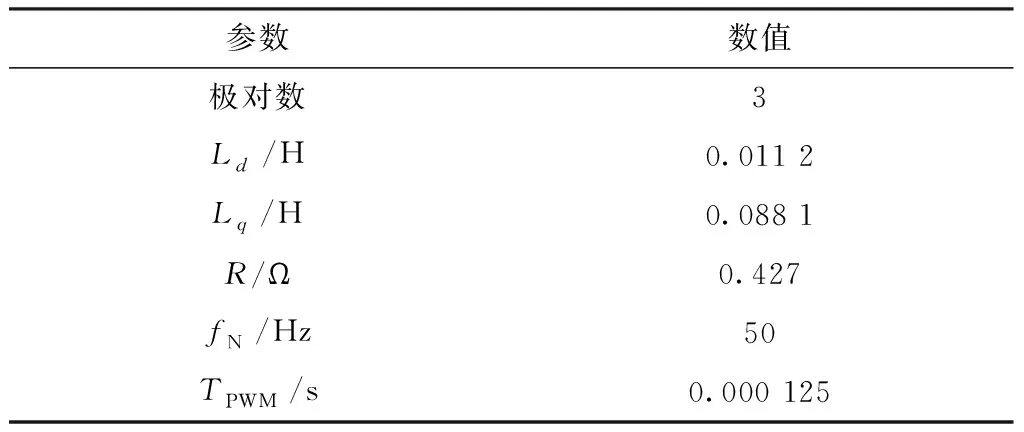
表1 電機模型仿真參數

嘗試在dq坐標系下抑制6次(300 Hz)諧波。根據前文的參數整定方法，取KR,d=300，ω0=300×2π rad/s，ωb=3 rad/s，系統的開環頻率響應如圖3所示。從圖3中可以看出，諧振環節提高了系統在諧振頻率的增益，此時系統的相位裕度為62°，滿足穩定性要求。

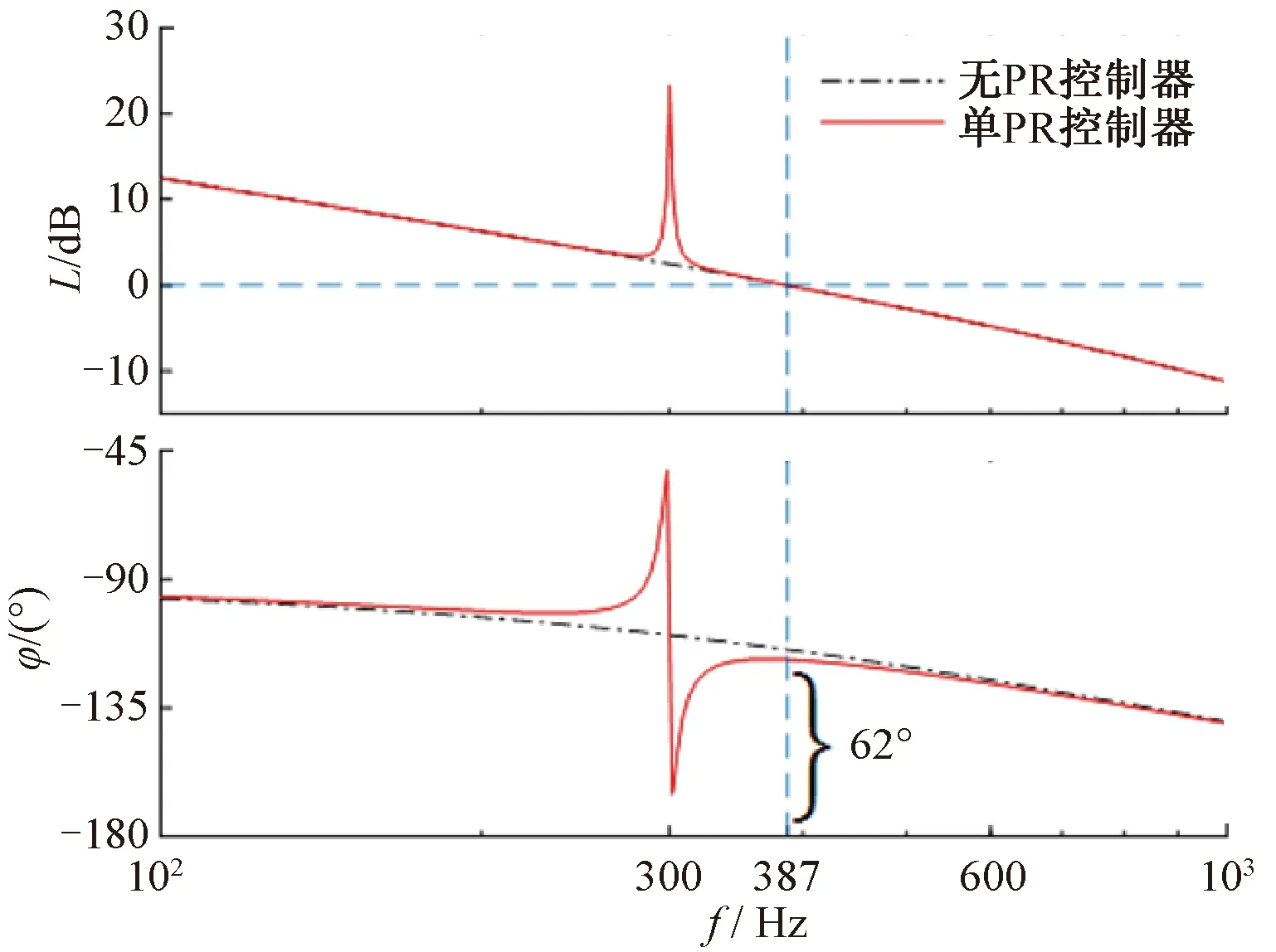
圖3 單PR控制器的系統開環頻率響應

該系統對6次電流諧波的抑制效果如圖 4和圖 5所示。PR控制器可將d軸上的6次電流諧波抑制到接近抑制前的四分之一，使得相電流中的5次和7次電流諧波也顯著降低。

圖4 PR控制器對6次諧波的抑制效果(相電流)

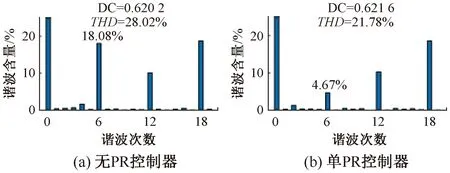
圖5 PR控制器對6次諧波的抑制效果(d軸電流)

然而，該系統的開環截止頻率僅有387 Hz，PR控制器無法抑制系統中存在的12次或18次高頻電流諧波。

3.2 ASVPWM

將電壓調制算法由SVPWM替換為ASVPWM后，系統的開環頻率響應如圖 6所示。由圖6可見，ASVPWM將開環帶寬由387 Hz提升至1 165 Hz，約為原值的3倍。此外，采用ASVPWM的系統具有更大的相位裕度，帶寬和穩定性均得到了提升。

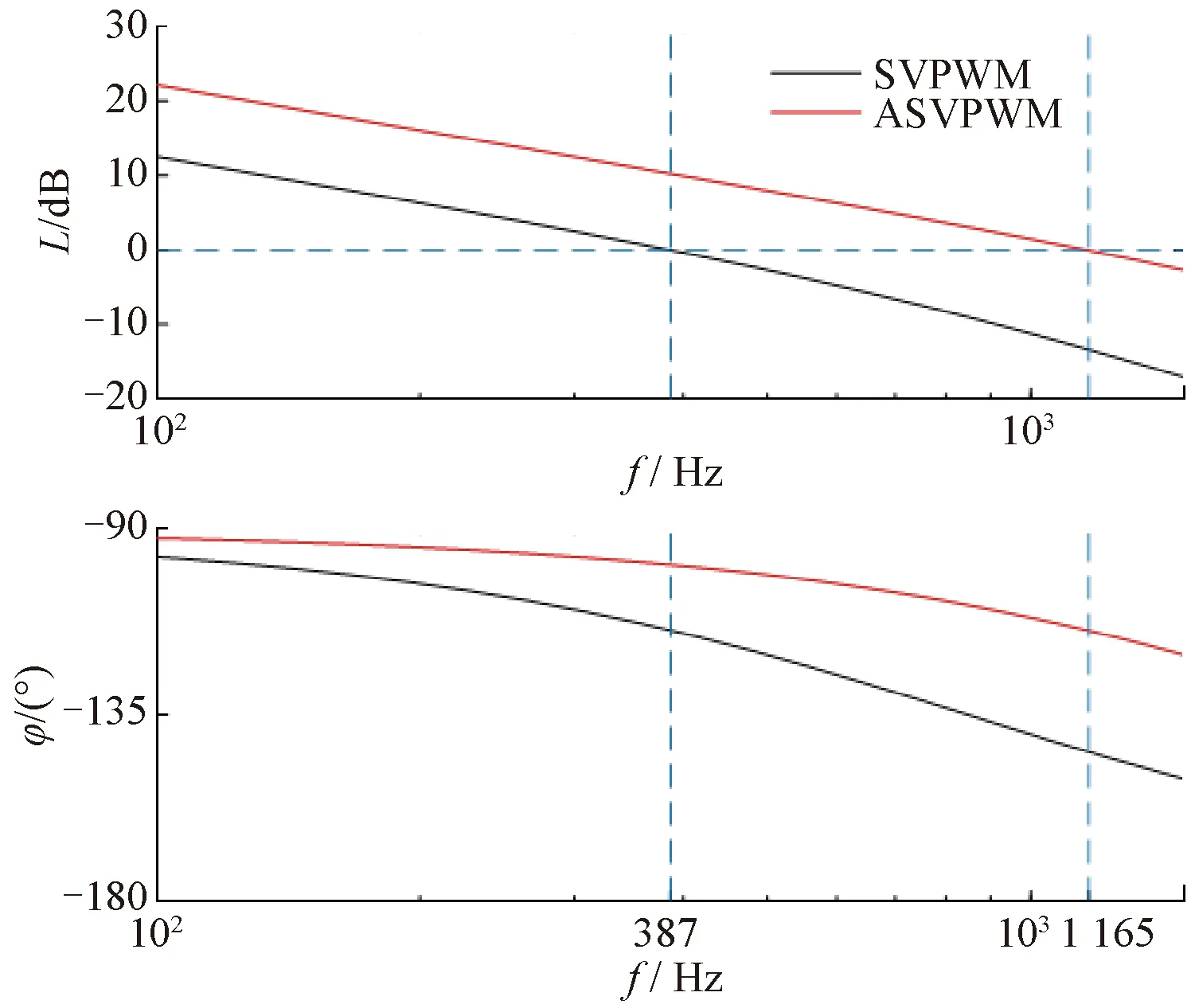
圖6 采用SVPWM/ASVPWM的系統開環頻率響應

現在嘗試通過多諧振控制器并聯的方式同時抑制6次(300 Hz)、12次(600 Hz)、18次(900 Hz)諧波。重新整定各參數，取ω0,6th=600π rad/s，ω0,12th=1 200π rad/s，ω0,18th=1 800π rad/s，KR,d6=KR,d12=KR,d18=5 000，ωb=3 rad/s，得到系統的開環頻率響應如圖7所示。

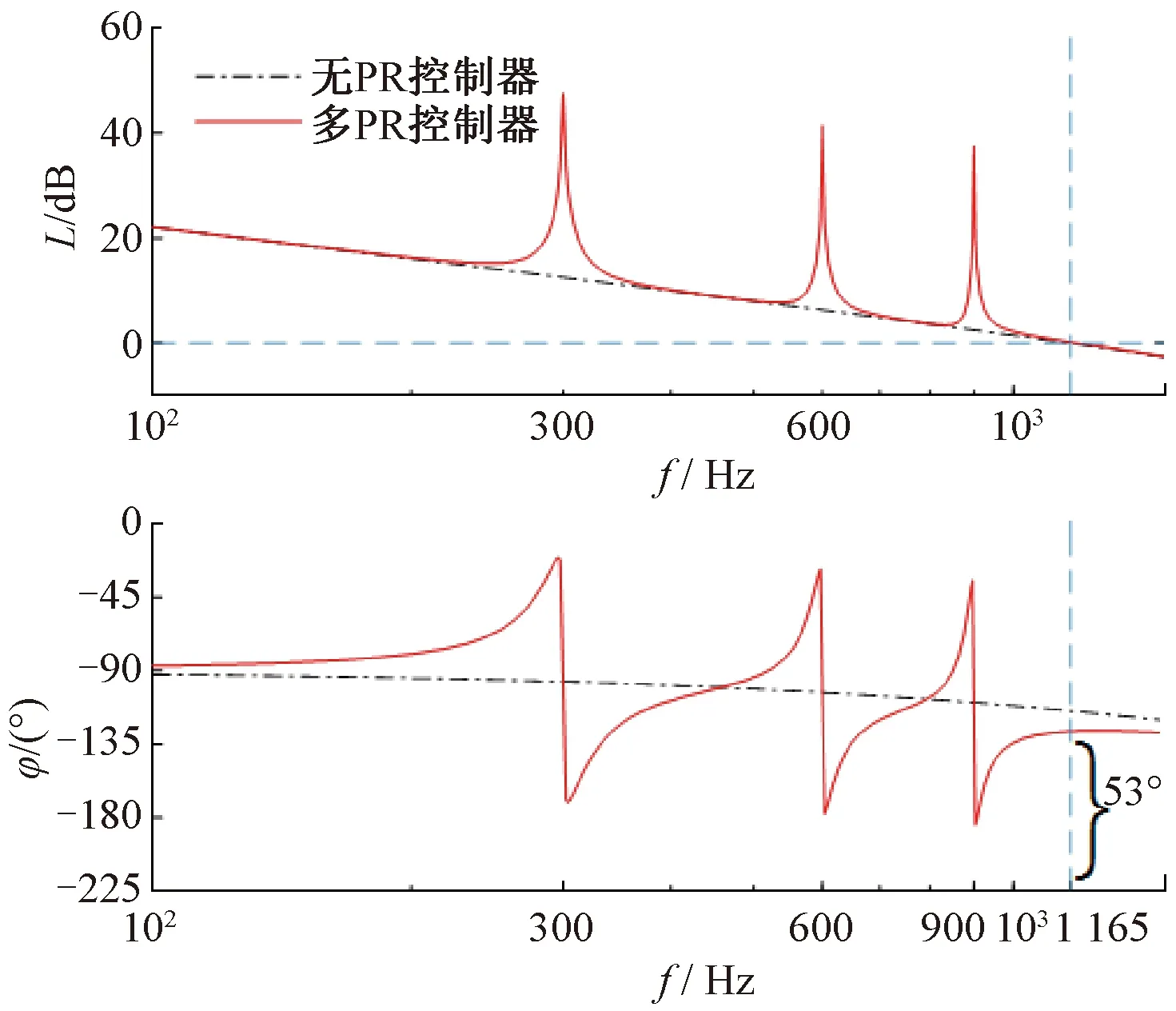
圖7 多PR控制器的ASVPWM系統的開環頻率響應

圖8和圖9展示了多PR控制器同步抑制多個頻率諧波的效果。在引入ASVPWM算法提升系統帶寬后，高頻的PR控制器可以有效抑制對應頻率的諧波，相電流的波形畸變得到了明顯改善。

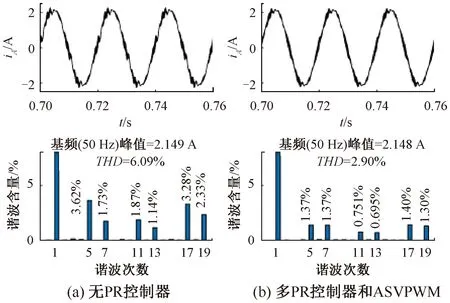
圖8 PR控制器和ASVPWM對6次、12次、18次諧波的抑制效果(相電流)

4 實驗及分析

4.1 實驗平臺介紹

本文通過在實驗平臺上進行樣機實驗以驗證PR-ASVPWM算法抑制高頻電流諧波的有效性。實驗平臺與環境如圖 10所示。

圖10 實驗平臺

實驗平臺中電機控制器以ST公司的STM32F407作為主控芯片，樣機為一臺功率1.5 kW的2對極混磁同步電機，PWM載波頻率為7.5 kHz，其余參數與仿真相同。實驗中使用Keysight DSOX2024A示波器采集電流信號且進行實時FFT分析，電機轉速與轉矩信號由HBM電機測量分析儀通過硬件傳感器采集，并顯示在上位機上。實驗負載為一臺帶有冷卻系統的恒壓供水水泵。

4.2 PR控制器諧波抑制實驗

在電機轉速為基頻50Hz的狀態下進行實驗。在未引入任何控制策略時，電機的轉矩、轉速波形與相電流的FFT分析結果如圖 11所示。從圖11中可以看出，電流中5、7、11、13、17、19次的原生諧波含量較大，對應d，q軸上的6、12、18次諧波。嘗試采用多PR控制器進行6、12、18次諧波的同步抑制，得到結果如圖 12所示。圖 12表明，引入PR控制器后，電機的轉矩脈動減小，電流中7次諧波含量顯著下降，幅值由-27.8 dB被抑制到-38.1 dB，但更高次的諧波抑制效果不明顯。這是因為諧振頻率高的PR控制器受系統帶寬限制，難以發揮作用所致。

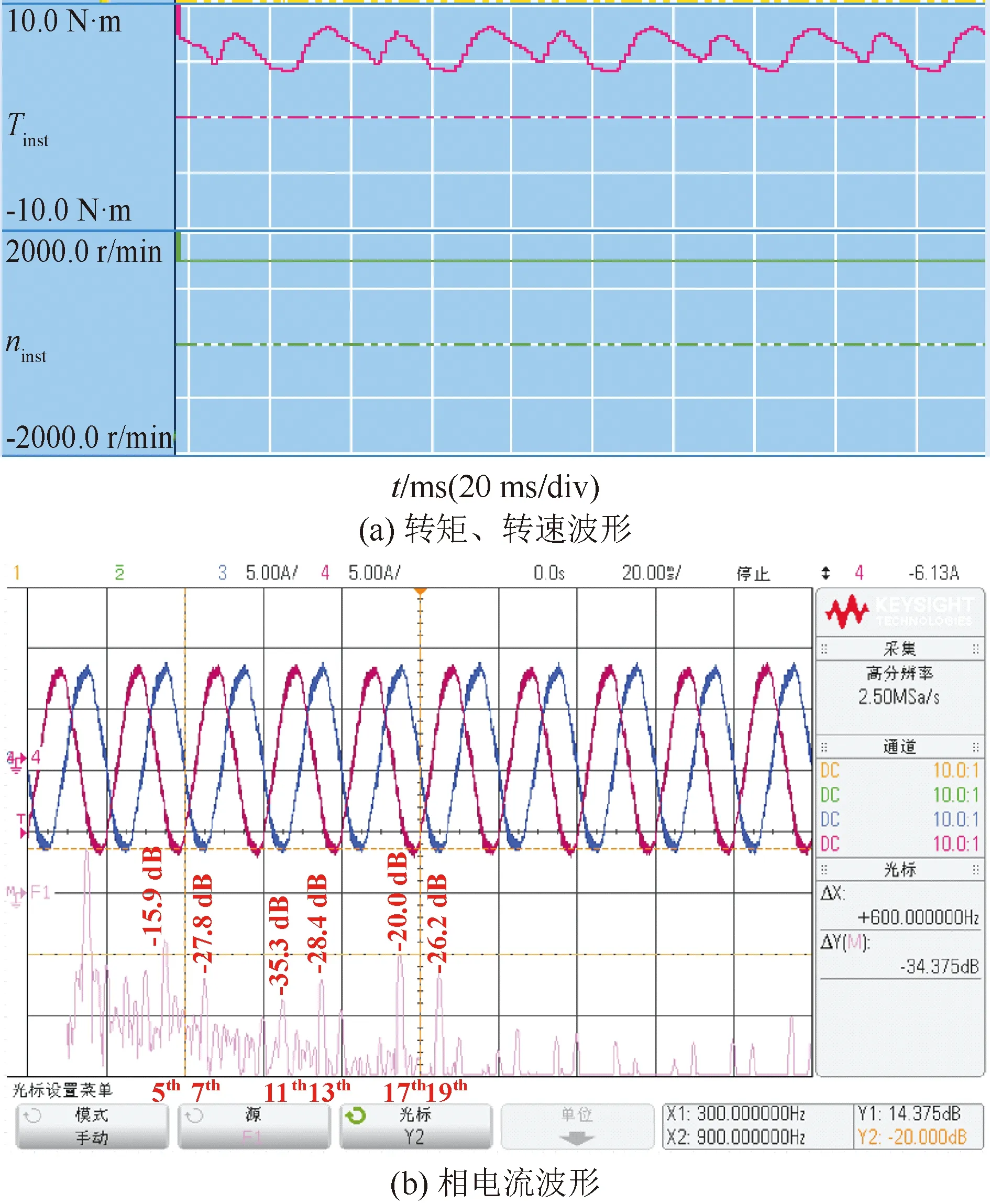
圖11 無控制策略時的波形

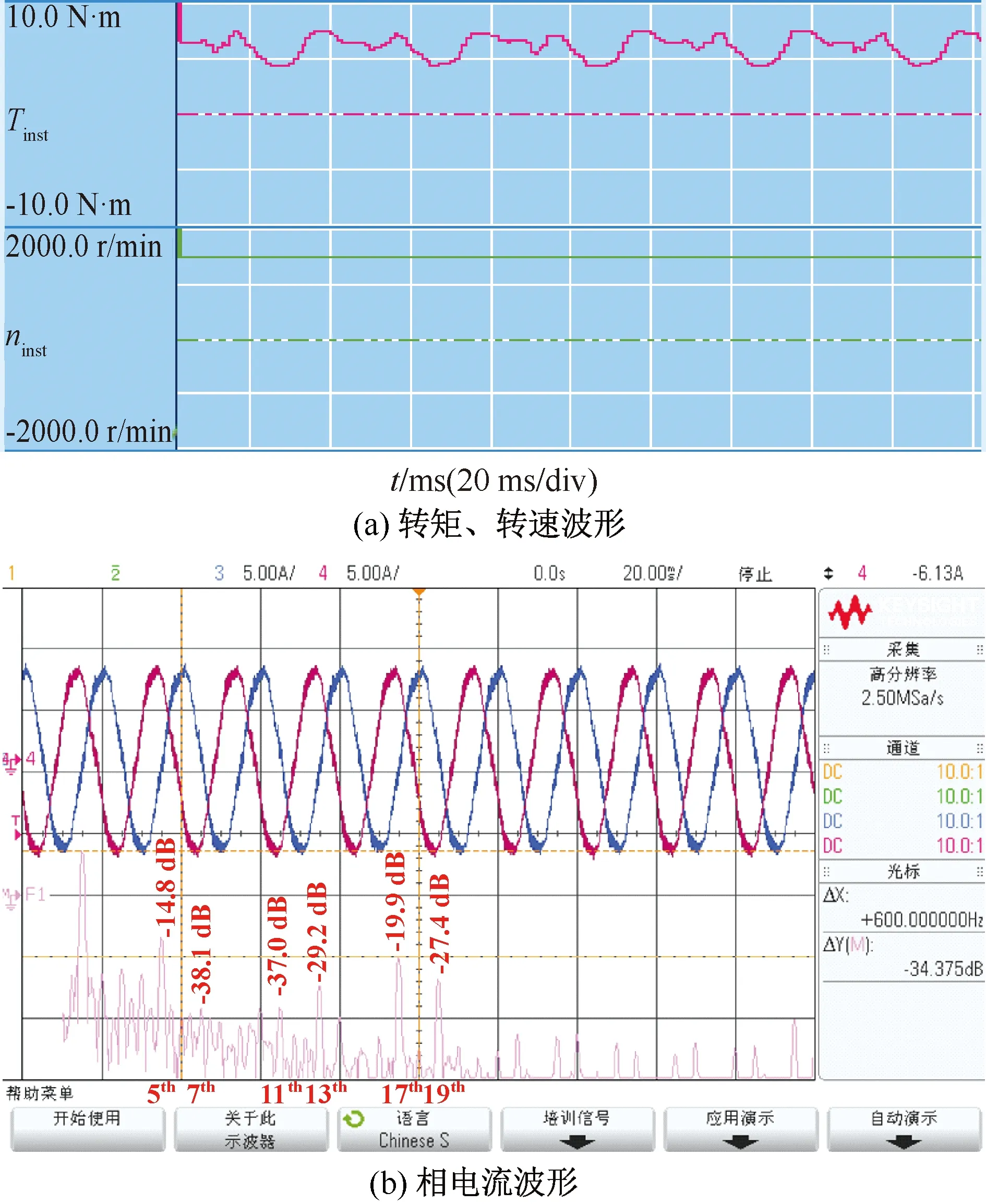
圖12 PR控制器諧波抑制效果

4.3 PR控制器和ASVPWM算法諧波抑制實驗

為實現對高次電流諧波的有效抑制，采用ASVPWM算法以提升系統帶寬，得到的波形如圖 13所示。

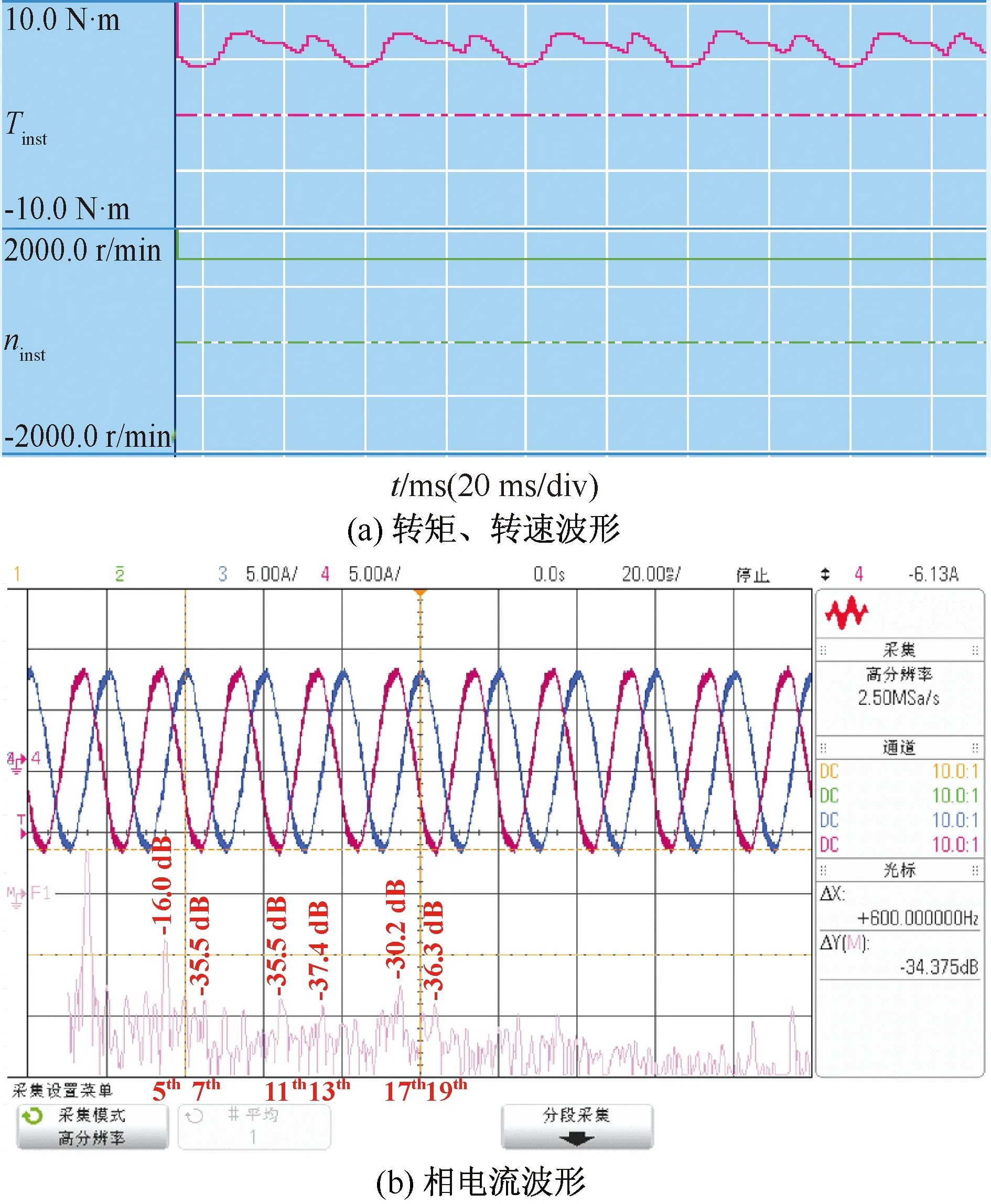
圖13 PR控制器與ASVPWM算法聯合的諧波抑制效果

從圖 13中可以看出，引入ASVPWM算法后系統帶寬提升，使得諧振頻率高的PR控制器可以有效作用于電流諧波上。其中，13次諧波從-28.4 dB被抑制到-37.4 dB，17次諧波從-20.0 dB被抑制到-30.2 dB，19次諧波從-26.2 dB被抑制到-36.3 dB，對應的諧波能量均被抑制到原來的10%左右，有效改善了電流波形，提升了正弦度。

5 結 語

在PMSM控制系統中，PR控制器可以有效抑制低頻電流諧波，但對于頻率高于系統截止頻率的諧波無能為力。本文的ASVPWM算法不但相較SVPWM具有更佳的諧波性能，而且能有效提升系統帶寬。在與ASVPWM結合后，PR控制器能夠實現對更高頻率電流諧波的抑制，并且可在PMSM變頻調速系統中實現多頻率的諧波抑制。